问题引领促发展 合作探究助提升

[摘 要] 为了更好地培养和发展学生的自主学习能力和合作探究能力,教师要认真研究教材、研究学生,针对不同的章节精心设计问题,努力打造一个自主学习与合作探究相结合的生态课堂环境,让学生在问题探索和解决过程中更好地理解知识、应用知识,提高学生的学习品质.
[关键词] 自主学习;合作学习;探究能力
问题是思维的起点,是探究的动力源. 在数学教学中,教师不仅要教给学生解决问题的方法,还要引导学生如何发现问题并提出问题. 课堂应以问题为主线,让学生在问题的驱动下积极思考,主动探究,探索性地获得知识,从而掌握技能,提升能力.
笔者以“平行四边形”第一课时为例,运用类比、多解、多变等方式让学生在问题解决的过程中学会思考、学会合作、学会交流、学会探索,以此提升学习品质,发展学习能力.
教学分析
对于平行四边形,学生并不陌生,在小学阶段他们已经初步了解了平行四边形. 同时,教学本节内容前,学生已经获得了探究等腰三角形、直角三角形等特殊图形的经验,这些知识与经验为新知的学习奠定了坚实的基础. 平行四边形作为又一个特殊图形,与前面已学的内容紧密联系,所以教学中教师可以从学生的已有经验出发,引导学生通过类比获得新知.
教学目标:(1)理解平行四边形的定义及相关概念;(2)掌握平行四边形边、角的相关性质;(3)应用新知解决问题,提高学生的数学应用能力;(4)借助独立思考、合作探究發展学生的探究能力,落实学生数学核心素养的培养.
教学简录
1. 新旧类比,引出主题
师:观看图片,你们发现了什么特殊图形?(教师PPT展示图片)
生(齐):平行四边形.
师:你们是如何判断的?(生积极交流)
生1:两组对边分别平行.
师:很好,之前我们已经学习了哪些特殊的图形呢?
生2:直角三角形、等腰三角形.
师:之前我们在研究这些特殊图形时,主要研究了哪些内容呢?
生3:主要研究了它们的定义、性质、判定、应用.
师:总结得非常好. 那么平行四边形作为特殊的图形,你认为我们应该研究它的什么内容呢?
设计意图 教学初,教师创设生活情境,让学生通过观察进一步感知平行四边形. 同时,引导学生与已学的特殊图形相类比,揭示课题.
2. 合作交流,理解定义
师:结合已学知识,你们认为应该怎样给平行四边形下定义呢?
在此环节,教师先让学生自主交流,然后引导学生提炼平行四边形的本质属性,最终学生通过合作交流准确地给出平行四边形的定义. 同时教师课件展示定义,以便学生理解和记忆.
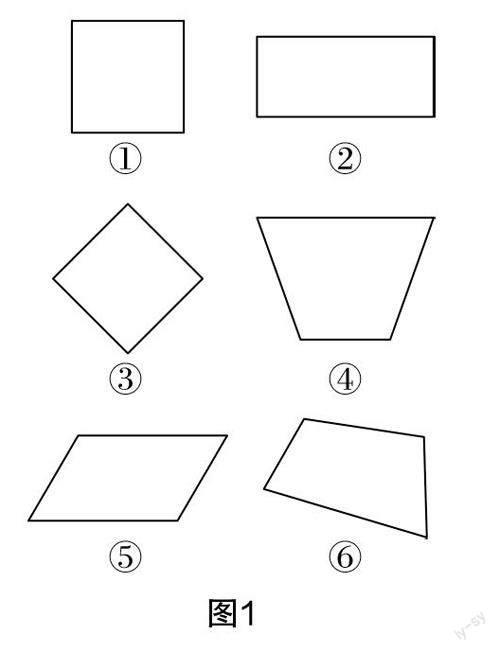
师:观察图1,其中哪些是平行四边形呢?(生积极思考)
生4:①②③⑤都是平行四边形.
师:很好,刚刚我们通过观察找到了平行四边形. 如果让你画一个平行四边形,你会吗?
设计意图 借助具体实例让学生观察、辨析,以此促进学生对概念理解的深化. 同时通过动手画,引导学生关注概念的本质,为后面的学习做铺垫.
3. 合作探究,归纳边、角性质
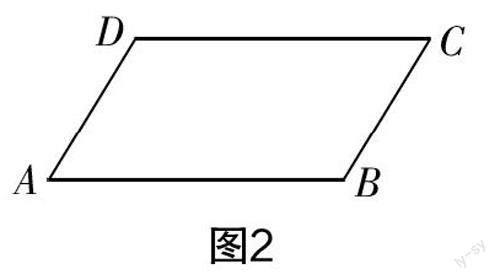
师:如图2所示,四边形ABCD为平行四边形,它的边有什么特性呢?
生5:对边平行. (生不假思索地回答)
师:还有吗?
生6:两组对边分别相等.
师:你判断的依据是什么?
生6:观察图2感觉对边应该是相等的,于是用尺子进一步测量,验证了猜想.
师:这是一个不错的方法,不过测量存在误差. 你们还有其他验证的方法吗?
教师预留时间让学生小组讨论、探索,很快学生就有了新的发现.
生7:连接AC,可以利用证明△ABC≌△CDA的思路来证明对边相等.
接下来,教师让学生独立完成证明过程. 教师巡视后,展示学生的证明过程,并进行总结、归纳.
师:刚刚我们一起研究了平行四边形边的特性,接下来我们还要研究什么呢?
生(齐):角的特性.
生8:根据上面的证明易知平行四边形的对角相等.
师:一定要利用证明全等的思路来验证吗?(师追问)
生9:哦,我知道了,可以直接利用平行线的性质来证明. (生恍然大悟)
师:通过以上分析,我们知道了平行四边形的边、角性质,即边——对边平行且相等;角——邻角互补,对角相等.
设计意图 在研究平行四边形边的性质时,教师引导学生将研究三角形的经验迁移至研究平行四边形,使得探究过程自然,这能有效地激发学生的学习积极性. 在研究平行四边形角的性质时,教师通过追问,让学生探寻不同的方法,激活了学生的已有经验,提升了学生的探究水平.
4. 巧用多解,发散思维
师:刚刚我们学习了平行四边形的定义,知道了平行四边形的边、角性质,现在请大家看看例1该如何证明. (教师PPT给出例1)
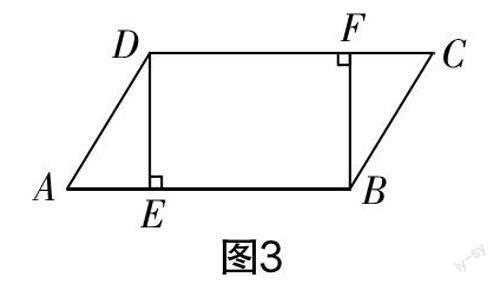
例1 如图3所示,在平行四边形ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F,求证:AE=CF.
问题给出后,教师让学生独立思考. 此题难度不大,学生很快就通过证明△ADE≌△CBF得到了结论. 教师投影学生的证明过程,并引导学生理解和掌握平行四边形边、角性质的用法.
师:若将结论改为“DE=BF”,又该如何证明呢?
生(齐):还是证明△ADE≌△CBF.
师:还有没有其他的证明方法?(生沉思)
生10:根据已知易得DF∥BE,DE∥BF,根据定义可知四边形DEBF是平行四边形. 于是可得DE=BF.
师:非常好,利用平行四边形的定义证明了结论,可见证明线段相等时未必都要用三角形全等. 我们要学会从不同的角度观察、分析、证明.
师:你们还能想到其他的证明方法吗?
学生思考、交流后,并未发现第三种证明方法,此时教师进行及时的引导和点拨.
师:请大家回忆一下小学的时候你们是如何求平行四边形面积的.
教师点拨后,学生豁然开朗,发现了第三种证明方法:S=AB×DE=CD×BF,又AB=CD,故DE=BF. 第三种方法思路简单,出奇制胜.
设计意图 在教学中,教师应充分挖掘例题、习题的内涵,鼓励学生尝试用不同的方法证明结论,让学生联想多种知识和方法,弄清知识之间的内在联系,帮助学生积累丰富的解题经验. 同时,教师还要引导学生从不同的角度进行分析,以拓宽学生的思维广度,激发学生的研究热情,促进学生分析问题和解决问题能力的提升.
5. 巧用多变,灵动课堂
师:刚刚我们通过结论变一变,找到了不同的证明方法,那现在我们把其他条件变一变,看看变化后又该如何证明. (教师PPT给出变式问题)
变式1 如图4所示,在图3的基础上画出直线AB和直线CD,在直线CD上任取一点P,过点P作PM⊥AB,垂足为M,则垂线段PM与DE之间存在怎样的数量关系?
问题给出后,学生立即回答“PM=DE”. 教师追问理由,学生指出,利用证明“DE=BF”的方法可证明PM=DE.
师:两条平行线间可以作多少条垂线段?它们之间存在怎样的数量关系?
学生小组交流后给出结论:两条平行线间可以作无数条垂线段,且这些垂线段均相等.
师:在图4中,若DE=10 cm,那么点P到直线AB的距离是多少?请说说你的理由.
生(齐):10 cm,两条平行线间的垂线段相等.
至此,通过师生互动,引出平行线距离的定义就变得水到渠成了. 为了进一步深化学生对相关概念的理解,教师可进一步进行变式拓展.
变式2 对于图4,在平行四边形ABCD中,若AD=AB,DE=10 cm,∠DAE=45°.
(1)求DF的长;
(2)求平行线AD,BC间的距离.
教师让学生通过小组合作的方式探究解题方法. 学生通过激烈的讨论和反复的交流,最终明确,求距离时需要将其转化为在直角三角形中来解决. 对于第(2)问,还可以应用面积法求解. 至此,有效的交流和合理的变式,让学生掌握了综合处理问题的方法. 在此基础上,教师还可以进一步拓展,将条件“∠DAE=45°”改为“∠DAE=30°”或“∠DAE=60°”,以进一步增强学生的应用能力.
设计意图 借助有效的变式让学生进一步巩固新知,培养学生思维的深刻性、变通性. 同时,借助变式引导学生发现平行线间的垂线段处处相等,继而引出平行线距离的定义,让学生亲身体验探究数学的乐趣,让课堂变得灵动.
6. 课堂小结,升华认识
该环节教师可以让学生通过互动交流的方式进行总结归纳,并通过交流、反思、回顾,优化学生的认知结构,让学生积累解题经验,从而提升学生的学习能力.
教学思考
在本节课的教学过程中,教师以问题为主线,引导学生通过独立思考和合作交流得到相关的定义、性质. 在教学中,教师从学生已有知识、经验出发,精心创设问题,让学生在问题的驱动下积极思考、主动探索,这能有效地激发学生的思维活力,提升学生的数学探究能力.
在上面的教学活动中,教师关注学生自主学习能力的培养和合作探究能力的提升,于是为學生创设了一个平等、和谐的交流环境,这能有效地提升学生参与课堂的积极性,能促进高品质合作探究课堂的生成.
总之,在教学中,教师应关注学生的发展,应通过合理的编排、悉心的指导为学生的思维搭建“云梯”,以此提高学生的自主学习能力和探究能力,提升学生的数学思维品质.
作者简介:赵龙(1988—),本科学历,中学一级教师,从事初中数学教学工作.

