可用于载人/ 物绿色爬楼装置爬行系统优化设计

庞元硕，杨玉维，郑巨烨，耿超群，李照童，宋宇昊

（1.天津理工大学天津市先进机电系统设计与智能控制重点实验室，天津 300384；2.机电工程国家级实验教学示范中心（天津理工大学），天津 300384）

1 研究背景

针对国内外现有较成熟的爬楼轮椅，依据其工作原理，可分为腿足式爬楼轮椅、行星轮式爬楼轮椅、复合式爬楼轮椅等，以上各种爬楼轮椅在实现爬楼方面都有其相应的局限[1]。日本早稻田大学和日本尖端机械企业Tmsuk 一同开发的“WL-16R”系列双足腿足机器人[2]以及上海交通大学设计开发出的两足载人步行椅机器人“JWCR”都具有较好的载人爬楼能力和灵活性，但由于其过低的能量运用效率，远达不到绿色的要求，复杂的控制要求与缓慢的移动效率也成为了不能忽视的问题[3-4]。日本的Sasaki K 设计研发的“Freedom”爬楼轮椅，其采用了双轮组四星行星轮设计，并且前轮组可以进行伸缩运动且差速离合原理保证爬楼梯过程中的平稳性及平地运动与爬楼运动的平滑切换，但也导致该型轮椅售价极其高昂[5-6]。

为解决以上难题，同时针对目前市面上主流的爬楼轮椅普遍价格昂贵、体积较大，对于老式、复式楼房狭小的楼道使用不便等问题[7]，本文提出体积小巧、结构简单、价格适中、行走平稳的可用于载人/物的绿色爬楼装置，并提出针对于该装置的稳定性指标——爬楼稳定度，在其基础上对该研究原型与样机进行深入分析与优化仿真。

2 整机设计

2.1 目标需求分析

根据GBJ 101-1987《建筑楼梯模数协调标准》[8]中所规定的楼梯尺寸，要求爬楼装置可在国内坡度为12°至30°之间的楼梯平稳运行。爬楼装置的负载不低于200 kg，保证载人载物时均可表现出良好的爬升性能且保证重心较为稳定。

2.2 爬楼装置整机设计

使用SOLIDWORKS 对于爬楼装置进行三维建模，其中各结构尺寸均按照成人体型与实际楼梯尺寸设计，爬楼装置整机结构见图1。

图1 爬楼装置整体结构

爬楼装置通过轮椅背部支撑支架与轮椅轮胎固定件固定轮椅，同时通过可调节机构实现爬楼装置与不同轮距、不同高度的轮椅相匹配。多排轮采用仿生设计，具有轴向伸缩性，在增大爬楼过程中与楼梯的接触的同时，保证了平稳性与安全性，避免过程中出现打滑、重心不稳等现象。电机作为主要动力来源。扶手用于进行人力辅助，实现人机交互。行星轮为爬楼装置的执行部件，具有伸缩功能，用于配合缓冲弹簧进行轴向伸缩运动，提高爬楼过程中的稳定性。

2.3 爬楼装置行星轮设计

新式行星轮因为缓冲弹簧的作用，可大幅降低攀爬台阶时产生的剧烈震动，达到平稳前进的效果。此新型装置在爬楼梯过程可以分为5 个状态，分别为压缩状态、完全压缩状态、翻越状态、伸展状态与完全伸展状态。本节的尺寸计算只涉及完全压缩状态与完全伸展状态两种瞬时状态，参考楼梯分别选择由调查得到的30°及实验得出的极限高度50°，两种状态两种楼梯共4 个类型的行星轮运动状态，见图2。

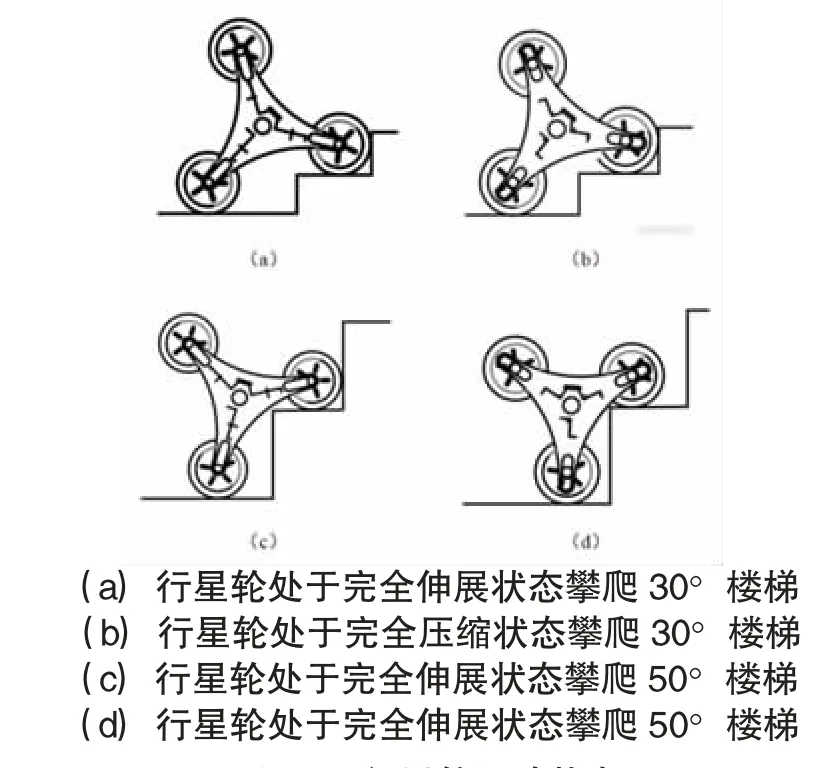
图2 行星轮运动状态

新式行星轮装置应满足在两种状态下都满足GBJ 101-1987《建筑楼梯模数协调标准》[8]所规定的各种楼梯指标。图3 为行星轮参数示意图，由图3可见计算公式中的各参数；表1 为行星轮及楼梯尺寸计算中的参数设置，由表1 可知各参数具体的名称及参数含义。

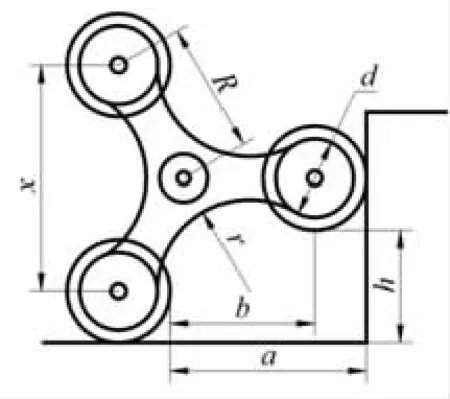
图3 行星轮参数示意图

推导可得行星轮星轮间中心距x 为

假设楼梯宽度a 范围为70 mm 至250 mm，楼梯高度h 范围为100 mm 至320 mm，计算可得

当楼梯宽度a=70 mm、楼梯高度h=70 mm 时，由式（3） 和式（4） 可得Rmin=75 mm。当楼梯宽度a=250 mm、楼梯高度h=320 mm 时，由式（3） 和式（4） 可得Rmax=234.5 mm。

假设行星轮星轮直径d 和行星轮臂长R 确定，行星轮轮架外板圆角半径r 推导可得

综上所述，行星轮主要参数设定为行星轮星轮直径d=36 mm，行星轮星轮间中心距x=160 mm，行星轮轮架外板圆角半径r=150 mm，行星轮臂长及可伸缩范围为R=105 mm～125 mm。

3 基于ASNSYS 的静力学分析

采用ASNSYS 进行有限元分析。对作为驱动轮的行星轮中具有主要支撑作用与限位作用的行星轮外板、作为在攀爬过程中需承受较大载荷的轮椅背部支撑支架与导向轮装置进行分析。对行星轮外板所施加的两种载荷，考虑到在爬楼过程中行星轮做翻转运动时对外板的压力角度，施加两种极端情况载荷加以分析，装置总设计质量为300 kg，取安全系数φ=1.5，对行星轮外板中心轴施加固定约束，a情况视作装置静止与地面时受力状态，b 情况视为行星轮在翻转爬楼时外板侧边极端情况受力及轮椅背部支架底部施加固定约束，模拟其使用时的实际情况，主要部件所受载荷与约束见图4。

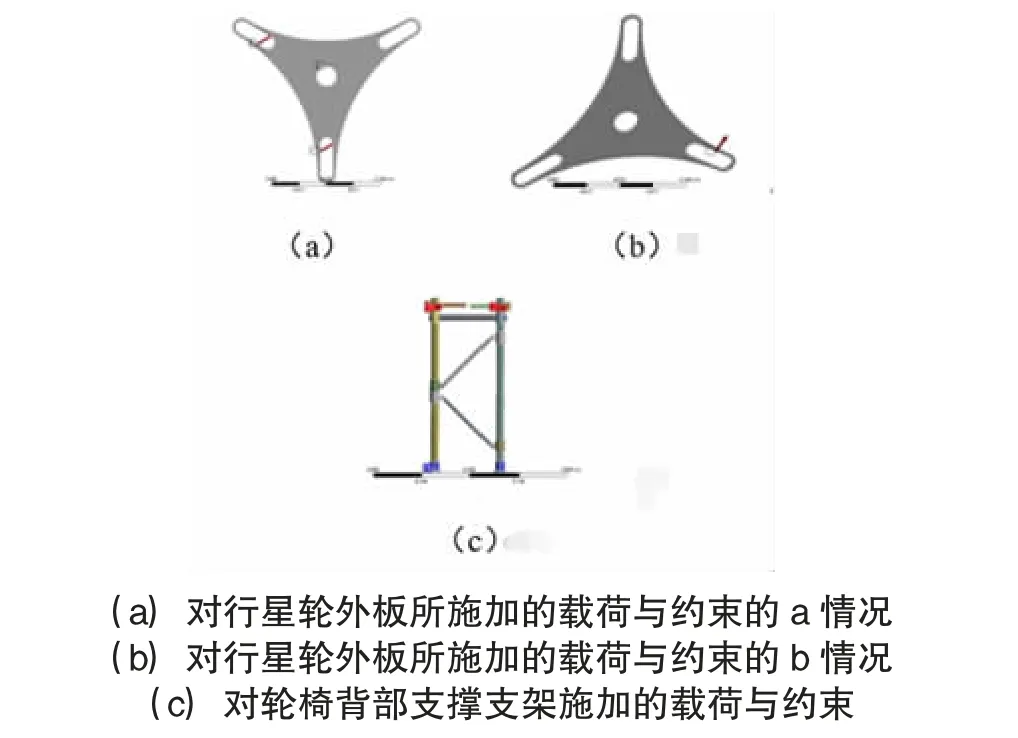
图4 主要部件所受载荷与约束

各项设置完成之后，通过解算可以得到零件各方向上应变、应力及变形等。本文主要考虑零件强度与刚度问题，故选取了等效应力分布云图与总形变分布云图作为输出结果并加以进行分析，得到若干分析结果。图5 为行星轮外板静力学分析结果1；图6 为行星轮外板静力学分析结果2；图7 为支撑支架静力学分析结果。

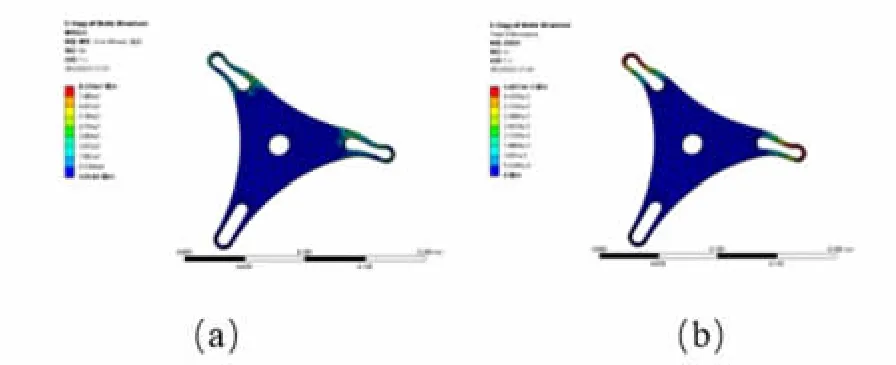
图5 行星轮外板静力学分析结果1

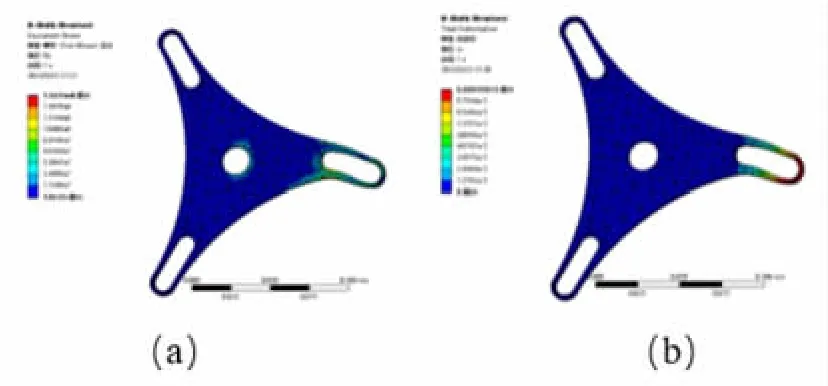
图6 行星轮外板静力学分析结果2

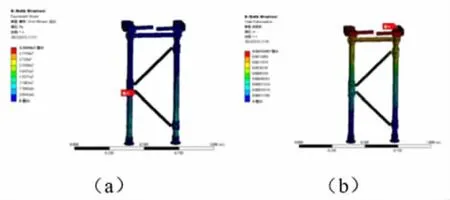
图7 支撑支架静力学分析结果

在图5～图7 中可看出各零件的最大形变与最大应力位置，为保证装置可以正常工作，最大应力应该小于材料的许用应力，安全系数φ=1.5，经计算得到各零件最大屈服强度，见表2。

表2 各材料最大屈服强度

进行对比可知材料处于许用应力范围内。最大形变值均发生在容许范围内，故基本可忽略不计，各材料性能的对比见表3。

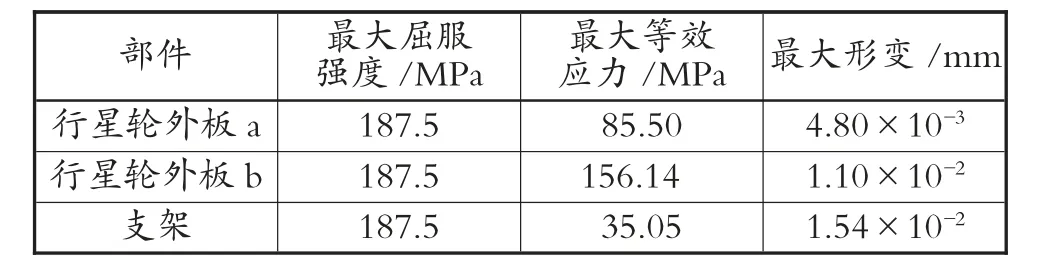
表3 各材料性能的对比表

4 基于虚拟样机技术的爬楼仿真

利用SOLIDWORKS Motion 软件搭建虚拟样机，进行爬楼仿真。为精简仿真结果，去除不必要的细节，尽可能对模型进行简化处理，因此不考虑电机和同步带的结构以及底盘上所载物品的具体形状。将简化模型导入到SOLIDWORKS Motion 工作环境之中。

对参数设定进行修改并多次仿真模拟。通过虚拟样机仿真获得实验数据，可得优化前后质心z 轴位移对比图，见图8。

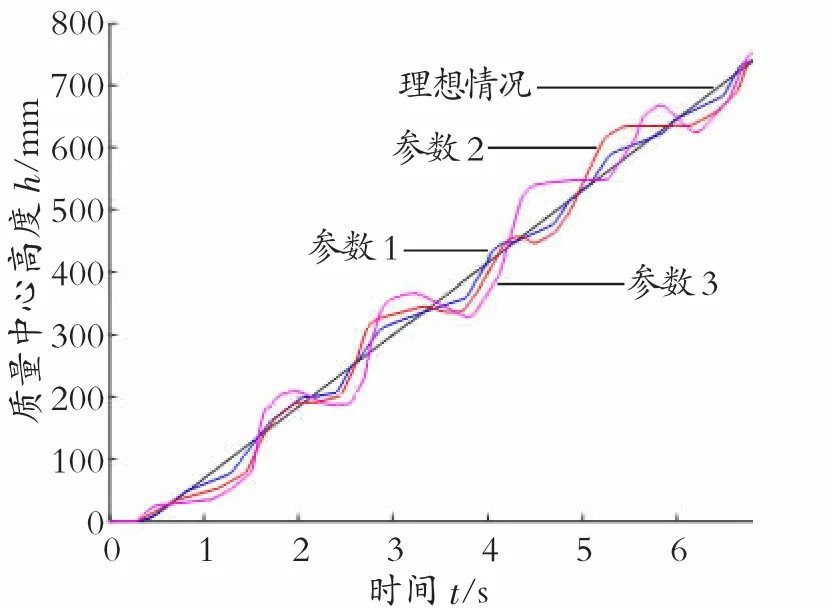
图8 优化前后质心z 轴位移对比图

为评价不同参数爬楼系统的平稳度，特提出爬楼稳定度指标K，其表达式为

式中：ωi为权数；K1、K2、K3依次为系统最大振动偏差、系统平均振动偏差、系统最大振动偏差与系统平均振动偏差的比值，其表达式分别为

式中：X 为实际位移；X0为理想位移；n 为样本数目。

在实际爬楼情况下，K1和K2两个指标更加重要，因此权重更大，分别取ω1、ω2、ω3为0.4、0.4、0.2。将仿真位移曲线导出样本并代入式（6） ～式（9），得到不同位移曲线的爬楼稳定度指标，见表4。

爬楼稳定度指标K 的值越小，其对应位移曲线的振动越小，优化效果越好。通过对比，可知曲线1 为最优情况，最优参数即为最终设定的SOLIDWORKS Motion 参数。见表5。

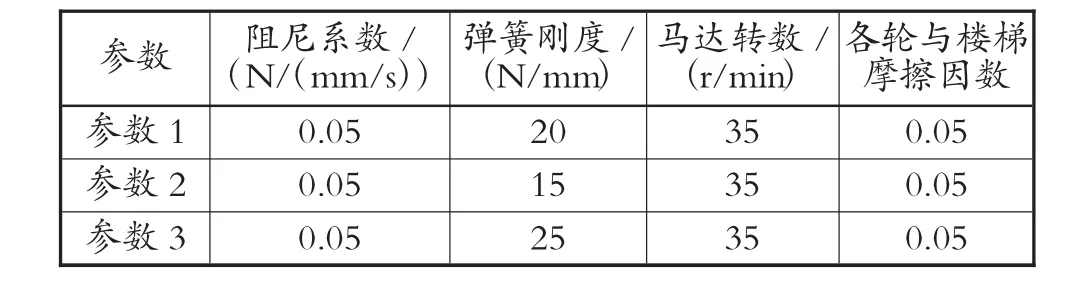
表5 最优参数

经过优化对比，爬楼装置竖直方向位移数值浮动均较小，说明爬楼装置质心位置能够稳定上升，爬楼过程较为稳定，缓冲装置作用明显。

5 结论

1） 基于特殊人群轮椅爬楼需求，设计了自适应助力绿色爬楼装置，建立了爬楼装置的三维模型，通过数学模型分析了行星轮的运行尺寸。

2） 在ASNSYS 中对主要部件进行静力学分析与材料强度校核，经过模拟，强度校核结果符合理论情况，在标准工况下不会发生断裂。

3） 在SOLIDWORKS Motion 中建立虚拟样机模型，将实际楼梯路况数据导入虚拟样机，对爬楼装置爬楼的过程开展动力学仿真分析，获得了爬楼装置运动时质心位移曲线，对于仿真结果进行进一步分析，通过修改爬楼装置参数与重复仿真，得到爬楼装置运行优化参数。