应用于低频电力系统的母线差动保护判据研究

丁 杰 吕 航 王风光 龚 啸 赵国勇

应用于低频电力系统的母线差动保护判据研究

丁 杰1,2吕 航1,2王风光1,2龚 啸1,2赵国勇1,2

（1. 南京南瑞继保电气有限公司，南京 211102；2. 南瑞集团公司（国网电力科学研究院），南京 211106）

随着清洁能源的快速发展，新能源结合柔性低频交流输电成为新的发展方向，为满足低频交流输变电系统的工程应用需求，常规交流继电保护须开展适应性研究。本文从母线保护出发，探讨现有母线保护原理，分析不同采样间隔对采样值积算法结果的影响。针对20Hz低频系统，基于采样值积算法提出一种低频母线差动保护新判据，利用采样值积算法快速计算故障特征量，并结合瞬时值判据保证故障判断的可靠性。测试结果表明，基于新判据的低频母线保护能够满足现有技术规范对母线保护的可靠性及速动性要求，母线区内故障时整组动作时间小于20ms，母线区外故障时低频母线保护可靠不动作。

新能源；低频电力系统；母线保护；采样值积算法；速动性

0 引言

交流输电具有变压简单、电流过零开断等特点，是目前主要的输变电方式，基于50Hz或60Hz的三相工频交流系统技术成熟，在国内外得到广泛应用。在远距离输电情况下，工频交流输电在长线路上的电压偏差及功率损耗较大，而直流输电则不受线路电抗约束，适用于远距离、大容量电能传输[1-3]，特别是柔性直流输电系统，因其具备动态电压支撑、潮流快速灵活控制等优势而获得快速发展，但直流输电也存在故障电流开断、直流变压等难题[4]。在直流与工频之间选择合适的输电频率，既能降低线路阻抗对功率传输的影响，又能保留交流输电的电磁感应变压、电流过零开断等优点，在长电缆线路输电、大规模新能源汇集等场景中，低频交流输电将成为工频交流和直流输电的有益补充，是值得深入研究的新型输电技术[5]。

低频输电技术是借助电力电子技术将50Hz工频交流电降低为15～25Hz低频交流电的新型输电技术，低频输电兼具工频系统组网灵活、电压等级易变换及直流系统远距离、大容量能量传输的优点，还具备功率控制、电压动态调整、异步电网互联等功能，柔性低频输电技术被认为在远距离、大容量输电、海上风电送出、海岛电网互联、城市电网等典型场景下较工频交流和柔性直流更具备技术经济优势[6-8]。我国目前已经对海风柔性低频典型方案和关键装备开展了广泛的研究，并建设了杭州柔性低频输电工程、台州柔性低频输电工程等示范工程。随着我国对清洁能源的不断重视，新能源如风力发电等已成为我国能源战略的重要组成部分，新能源结合柔性低频交流输电将成为新的发展方向。

继电保护是电力系统安全稳定的第一道防线，低频输变电系统的应用必然要求与之匹配的低频继电保护装置，基于50Hz电力系统研制的继电保护装置显然无法直接应用于低频电力系统，而现有技术中，鲜有关于低频输变电继电保护的研究。为适应低频交流输电的工程应用，常规交流继电保护亟需开展适应性研究。比较简单的做法是，将基于50Hz工频系统的电气量保护算法通过降低采样频率来适应低频输变电系统，即保证一个交流整周波信号的采样点数不变即可。这种方法虽然简单，但会大大降低继电保护装置的速动性，以20Hz低频交流系统为例，电压、电流等电气量的全周傅里叶算法时间窗将由20ms延长为50ms；半波积分算法时间窗将由10ms延长为25ms，时间窗的延长将使继电保护设备的动作速度难以满足速动性要求，给一次设备的安全可靠运行带来巨大风险。

母线是电力系统的重要元件，母线故障是最严重的电气故障之一，母线保护装置是保障变电站母线长期稳定运行的有效继电保护装置。现有技术规范要求系统故障发生后，母线保护应能快速隔离故障，整体故障切除时间应不大于20ms。在低频输电系统中，受换流器的短路电流承受能力限制，低频输电系统对故障的快速识别及隔离提出了更高的要求，如果不对母线保护原理进行适应性改造，就无法保证低频系统的安全可靠运行。

本文从母线保护在低频交流输电系统中的应用出发，对现有母线保护进行适应性改造，并提出一种低频母线差动保护新判据，以提高低频母线保护装置的速动性，为低频输变电系统可靠运行提供可靠的设备支撑。

1 现有母线差动保护原理

母线保护是电力系统一次母线的主保护装置，母线故障不能及时切除，将对一次系统的安全稳定运行产生严重影响，因此对母线保护的速动性有很高要求。

比率制动差动保护[9-10]是目前嵌入式微机母线保护的主要工作原理，但具体实现方式又有不同，主要包含两大类：一类是基于差流瞬时值的采样值差动保护；另一类是基于差流幅值或有效值的差动保护，本文统称为幅值差动保护。

1.1 采样值差动保护

采样值差动保护[11-12]计算每一个采样时刻的差动电流、制动电流，判断是否满足比率制动特性。由于采样值随时间周期性变化，导致对每一个采样点而言，其制动特性并不一样。为保证动作判据的正确性，通常采用重复多次判别的方式，即若连续次采样判别中有次以上满足保护动作判据，则保护动作。由于采样值的随机性，采样值差动保护判据存在很大的模糊区，连续采样点数、重复判断次数的合理选取是改善采样值差动保护安全性和灵敏度的关键技术之一。文献[11]指出，确保采样值差动保护的制动性能不低于幅值差动保护的连续时间窗对应的角度需在90°以上。文献[12]指出，为保证采样值差动保护克服CT饱和及其带来的暂态响应的影响，需加大判别数据窗，动模试验表明，判别数据窗应大于180°才可保证区外CT饱和时不误动。

由上述采样值差动保护原理可知，为确保动作判据的可靠性，需要连续次采样进行比率特性判断。显然，低频输电系统相较于50Hz输电系统，相同数据窗对应的采样时间必然更长，如何兼顾采样值差动保护的可靠性和速动性是值得研究的课题。

1.2 幅值差动保护

基于幅值（或有效值）的差动保护，其本质是利用实时采样值计算出故障特征量，例如差动电流的幅值，然后再做故障判断。

对于如何获取故障特征量，有关学者提出了多种算法，如傅里叶算法、积分算法、最小二乘法、卡尔曼滤波算法[13-16]等。

幅值差动保护的优势在于，用于故障判断的启动电流、制动电流及比率制动系数都有其明确含义，能够进行准确计算、明确整定。

嵌入式微机继电保护在选择故障特征量算法时，需要根据模拟量信号的周期，综合考虑嵌入式系统的计算能力及继电保护装置速动性的要求，因此通常选用计算量小、时间窗相对短的算法。

2 低频母线差动保护判据

2.1 采样值积算法

一个正弦函数可由三个基本特征量表示，即幅值m、初相位和角频率=2p。为了求解上述三个未知数，需要建立三个独立方程。利用三个不同时刻的采样值可以建立式（1）所示的方程组。

式中：为采样间隔；i为t时刻的采样值。求解上述方程组，可确定正弦函数的三个基本特征量，说明只需要三个采样值就能得到包括幅值m在内的正弦函数的全部特征量。

对于电力系统而言，由于其频率波动较小，因此可认为信号频率为已知，这样待求未知特征量就减少为两个，只需要两个不同时刻的采样值就能求得幅值和相位，这种特征量计算方法称为采样值积算法，依靠两个不同时刻采样值的算法称为两采样值积算法[17]，依靠三个不同时刻采样值的算法称为三采样值积算法。下面以两采样值积算法为例加以说明。

取式（1）中前两个等式，将两式相加得

式中，s为采样周期。

将两式相减得

将式（2）、式（3）分别取平方后再相加可得

式（4）中，采样间隔和采样周期s在采样率固定时为常数，相应三角函数可提前算出，不会带来过大的计算量。式（4）表明，利用当前时刻采样值i和间隔个采样点的历史采样值i-，即可获得信号幅值，显然值越小，计算幅值的时间窗越短。

下面以20Hz正弦信号为例，分析不同值及信号初相位下两采样值积算法计算信号幅值的响应。

采用式（5）所示的正弦信号，其信号初相位可任意设置。

式中，为被采样信号。采用1 200Hz作为信号采样率，信号初相位a 设为0°，式（4）中采样间隔K分别取2、3、4、5，以第60采样点时刻作为y信号触发时刻，可得到图1所示不同K值下的幅值曲线。图1中，y为被采样信号，仅显示1/2周波。

信号初相位设为90°，式（4）中采样间隔分别取2、3、4、5，可得到图2所示不同值下的幅值曲线。

由图1和图2可知，两采样值积算法能够准确计算出被采样信号的有效值，并且采样间隔值越小，计算出稳态有效值的速度越快，值表征了采样值积算法计算稳态幅值的最短时间窗。另一方面，在信号突变时刻，采样值积算法在其必要时间窗之前将计算出不稳定的异常幅值，并且异常幅值大小与值和信号初相位都有关，值选取得大，虽然计算出稳态幅值需要更长时间，但不稳定区间内异常幅值偏离真实值相对更小。其他值或信号初相位的测试均能得出以上结论，本文不再赘述。考虑到采样值积算法在波形突变时刻将计算出不稳定的幅值，实际应用时可适当延时，以躲过不稳定时间窗、提高算法的可靠性。

图2 a =90°时不同K值下的幅值曲线

2.2 与半波积分算法比较

半波积分算法是微机保护常用的特征量算法，时间窗仅需半个周波，计算量相对小，在现有微机继电保护中获得广泛应用。下面以典型的电力系统故障短路电流作为输入，对比两采样值积算法与半波积分算法的响应情况。

由电力系统故障分析理论可知，无穷大系统发生接地短路故障后，若忽略负荷电流的影响，则短路电流的解析表达式为

式中：为短路电流瞬时值；为时间；为角频率；m为短路电流稳态幅值；为电源合闸角与故障阻抗角的相位差；为非周期分量衰减时间常数。

设短路电路稳态有效值为1A，系统频率20Hz，衰减时间常数取0.1s。采用式（4）的两采样值积算法并取采样间隔为5，另外为提高可靠性，本文对两采样值积算法设置8个采样点的延时，以躲开故障起始时刻的不稳定时间窗。同时，考虑到非周期分量的存在，采用前置差分滤波算法削弱非周期分量对采样值积算法及半波积分算法的影响。

以第60采样点作为故障触发时刻。当故障相位差=0°时，两采样值积算法和半波积分算法对比如图3所示。从图3可以看出，此时短路电流中无非周期分量，短路后直接进入稳态。虽然两采样值积算法幅值输出设置了采样延时以躲过不稳定时间窗，但仍比半波积分算法更快得出短路电流有效值，提前了约20ms。

图3 q =0°时两采样值积算法和半波积分算法对比

当故障相位差=-90°时，短路电流中非周期分量最大，两采样值积算法和半波积分算法对比如图4所示。短路电流在短路后半个周波达到最大值，而由于非周期分量的存在，使得计算有效值以真值为中心轴作小幅摆动，相较于半波积分算法，采样值积算法依然表现出了良好的性能。

图4 q =-90°时两采样值积算法和半波积分算法对比

由图3和图4可见，故障发生后，两采样值积算法相较于半波积分算法，能以更短的时间窗提取出故障特征量，因此在进行故障特征判断时，采样值积算法在速动性方面具有明显优势。其他故障角度的计算结果均支持上述结论，本文不再赘述。

2.3 基于采样值积算法的低频母线保护判据

下面以20Hz低频系统为研究对象，说明基于采样值积算法的母线保护新判据。

对于50Hz交流系统，继电保护相关规范要求采样率不低于1 000Hz，在满足采样定理的前提下，考虑嵌入式系统的计算能力，本文选择1 200Hz作为20Hz低频交流系统的继电保护采样率。

为进一步降低计算量，并尽可能保证继电保护的速动性，将式（4）中的两采样值间隔设置为5个采样中断，可计算出电流有效值为

式中：i为t时刻的采样瞬时值；I为t时刻采样有效值。

计算式（7）所需的时间窗为6个采样周期，对于20Hz的周期信号耗时约5ms，可以简单、快速地计算出电气量有效值。

微机母线保护在离散采样得到母线电压、各支路电流的瞬时值后，可利用式（7）计算出母线电压、支路电流的有效值；将各支路电流采样值按其差动构成叠加可得到差流瞬时值，然后利用式（7）可计算出差流有效值。

假设参与差动计算的支路数为，时刻支路瞬时采样值为i_k，则差流瞬时值为

根据式（7）可得差流有效值为

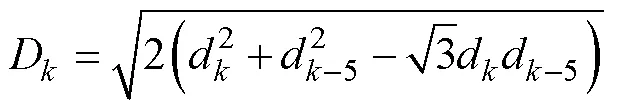
时刻支路有效值为

将各支路电流有效值累加得到制动电流有效值为

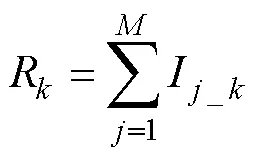
必须指出，采样值积算法计算式基于理想正弦波推导得出，而对于实际的电力系统，除工频分量外，其故障电流、电压中通常含有复杂的故障分量，如非周期分量和各次谐波分量，有学者提出多种数字滤波算法[18-21]。实际上，目前微机继电保护算法通常基于工频分量推导得出，再辅以适当的措施解决非工频分量的干扰，从而形成具备工程应用价值的实用算法。例如，对于非周期分量，通常采用差分算法近似地将直流分量滤除，但由于衰减时间常数不尽相同，时间常数越小直流分量衰减得越快，差分滤除效果也就越差；对于谐波分量，对动作速度有较高要求的保护元件，例如突变量差动保护，无法完全滤除谐波分量，对动作速度要求不高的保护元件，通常可使用傅里叶算法等滤除谐波分量，提取出工频分量。

为进一步提高采样值积算法的可靠性，本文采用瞬时值判据作为采样值积算法的辅助判据，即当差流瞬时值达到差动启动门槛值之上时才认为发生了故障。

假设差流波形为正弦波，P取值为1，以0°作为故障差流起始角，故障差流波形如图5所示。在故障角度达到45°时，差流瞬时值越过启动门槛值。实际继电保护定值整定计算中，差动启动定值一般考虑最小故障电流时仍有一定的灵敏度，因此实际故障时，瞬时值判据的动作速度会更快。

互感器饱和是母线保护无法回避的问题，本文着重于如何更快地提取出故障特征量，可靠地识别出故障，对于电流互感器饱和的识别与防误，可继续沿用现有成熟的保护判据，如时差法或波形识别法[22-24]等。

综上，基于采样值积算法的低频母线差动保护判据为

式中：D为差动电流有效值；R为制动电流有效值；d为差动电流瞬时值；set为差动保护启动电流定值；为比率制动系数，推荐取值0.3～0.8。

3 动模验证

为验证本文保护算法的有效性，基于实时数字仿真器（real time digital simulator, RTDS）系统，搭建如图6所示的测试系统。测试系统由工频变压器、交流变频器、低频变压器及低频输电线路组成，低频输电系统额定频率为20Hz。设置F1为低频母线区内故障点，设置F2为低频输电线路区内即母线区外故障点。

图6 测试系统

主变参数见表1。分别模拟母线区内、外各种类型的短路故障，测试结果见表2，其中A、B、C分别为故障相别，N表示接地故障，如AN表示A相接地故障，AB表示A相、B相相间短路故障。

表1 主变参数

表2 测试结果

以A相接地短路故障为例，故障持续时间约100ms，区内故障录波如图7所示，区外CT饱和故障录波如图8所示。

图7 区内故障录波

图8 区外CT饱和故障录波

测试结果表明，本文所述低频母线保护新判据能够保证母线区内故障时可靠动作、区外故障时可靠不动作，并且区内故障的切除时间小于20ms，满足母线保护可靠性及速动性的要求。

4 结论

本文从母线保护出发，探讨继电保护设备应用于低频电力系统的适应性改造，基于采样值积算法，提出了低频母线保护新判据，判据利用采样值积算法结合差流瞬时值，能够快速识别出区内故障。动模验证表明，本文提出的低频母线保护新判据具有良好的保护性能，能够应用于低频电力系统母线保护，依据该判据开发的低频母线保护装置已有工程应用。需要指出的是，本文所述保护算法经适当改造后亦可应用于低频变压器、低频输电线路等低频设备的二次保护，在低频输变电系统中具有广阔的应用前景。

[1] 孙冠群. 海上风电场全直流汇集经济性研究[J]. 电气技术, 2023, 24(5): 1-5.

[2] 高晨, 赵勇, 汪德良, 等. 海上风电机组电气设备状态检修技术研究现状与展望[J]. 电工技术学报, 2022, 37(增刊1): 30-42.

[3] 陆晶晶, 贺之渊, 赵成勇, 等. 直流输电网规划关键技术与展望[J]. 电力系统自动化, 2019, 43(2): 182- 191.

[4] 汤广福, 庞辉, 贺之渊. 先进交直流输电技术在中国的发展与应用[J]. 中国电机工程学报, 2016, 36(7): 1760-1771.

[5] 赵国亮, 陈维江, 邓占锋, 等. 柔性低频交流输电关键技术及应用[J]. 电力系统自动化, 2022, 46(15): 1-10.

[6] 黄明煌, 王秀丽, 刘沈全, 等. 分频输电应用于深远海风电并网的技术经济性分析[J]. 电力系统自动化, 2019, 43(5): 167-174.

[7] 汪大洋, 刘宗烨, 李沛, 等. 基于模块化多电平矩阵换流器的海上风电分频系统经济性分析[J]. 分布式能源, 2018, 3(2): 16-22.

[8] 林进钿, 倪晓军, 裘鹏. 柔性低频交流输电技术研究综述[J]. 浙江电力, 2021, 40(10): 42-50.

[9] 陆征军, 李栋, 毛亚胜, 等. 微机母线保护的母线运行方式自适应方案[J]. 电力系统自动化, 1999, 23(10): 41-44.

[10] 王风光, 李力, 吕航, 等. 新一代分布式母线保护装置[J]. 电气技术, 2022, 23(8): 62-67.

[11] 陈德树, 马天皓, 刘沛, 等. 采样值电流差动微机保护的一些问题[J]. 电力自动化设备, 1996, 16(4): 3-8.

[12] 胡玉峰, 陈德树, 尹项根. 采样值差动及其应用[J].电力系统自动化, 2000, 24(10): 40-44.

[13] 罗谌持, 张明. 基于Sigma点卡尔曼滤波器的电力频率跟踪新算法[J]. 电力系统自动化, 2008, 32(13): 35-39.

[14] 王永刚, 孙羽苗, 张楠楠, 等. 基于无迹卡尔曼滤波的非线性解耦方法在火电机组中的应用研究[J]. 电气技术, 2021, 22(8): 15-24.

[15] 王明磊, 常湧. 半周积分算法的几种改进算法[J]. 电力系统保护与控制, 2009, 37(11): 66-69.

[16] 黄家栋, 陈达壮, 张玲. 基于两点乘积算法的变压器励磁涌流识别新方法[J]. 电网与清洁能源, 2010, 26(9): 4-8.

[17] 张保会, 尹项根. 电力系统继电保护[M]. 2版. 北京:中国电力出版社, 2010.

[18] 叶宗彬, 侯波, 张延澳, 等. 一种三相对称系统快速谐波检测算法[J]. 电工技术学报, 2023, 38(2): 510- 522.

[19] 袁宇波, 陆于平, 刘中平. 基于相量法的短数据窗快速滤波算法[J]. 电力系统自动化, 2004, 28(3): 58-63.

[20] 李斌, 李永丽, 贺家李. 一种提取基波分量的高精度快速滤波算法[J]. 电力系统自动化, 2006, 30(10): 39-43.

[21] 段玉倩, 常宝波, 贺家李, 等. 一种用于微机继电保护的实用滤波算法[J]. 电力系统自动化, 2004, 28(23): 71-74.

[22] 黄梓欣, 林湘宁, 马啸, 等. 含风电继电保护应用中的电流互感器饱和电流重构方法[J]. 电工技术学报, 2022, 37(19): 4823-4834.

[23] 陈建玉, 孟宪民, 张振旗, 等. 电流互感器饱和对继电保护影响的分析及对策[J]. 电力系统自动化, 2000, 24(6): 54-56.

[24] 沈全荣, 严伟, 梁乾兵, 等. 异步法电流互感器饱和判别新原理及其应用[J]. 电力系统自动化, 2005, 29(16): 84-86.

Research on bus differential protection criterion applied to low frequency power system

DING Jie1,2LÜ Hang1,2WANG Fengguang1,2GONG Xiao1,2ZHAO Guoyong1,2

(1. NR Electric Co., Ltd, Nanjing 211102; 2. NARI Group Corporation (State Grid Electric Power Research Institute), Nanjing 211106)

With the rapid development of clean energy, new energy combined with flexible low frequency AC power transmission has become a new development direction. In order to meet the engineering application requirements of low frequency AC power system, adaptability research must be carried out for conventional AC relay protection. Starting from the busbar protection, this paper discusses the existing busbar protection principle, and analyzes the influence of different sampling intervals on the result of sample value product algorithm. For 20Hz low frequency power system, a new criterion for low frequency bus differential protection is proposed based on the sample value product algorithm. The fault characteristic quantity is quickly calculated based on sample value product algorithm, and the reliability of fault judgment is guaranteed by combining with instantaneous value criterion. The simulation results show that the low frequency busbar protection based on the new criterion can meet the requirements of the existing technical specifications for the reliability and speed of busbar protection. The whole fault clear time is less than 20ms for faults within the busbar area, and the low frequency busbar protection does not operate for faults outside the busbar area.

new energy; low-frequency power system; busbar protection; sample value product algorithm; speed

2023-08-10

2023-09-09

丁 杰（1985—），男，江苏省徐州市人，硕士，高级工程师，主要研究方向为继电保护专业的产品研制与开发。