求解二阶锥绝对值方程组的惯性two-sweep 迭代法

洪晓曼，唐嘉

（福建师范大学 数学与统计学院，福建 福州 350007）

绝对值方程问题(AVE)是数学规划中的一个重要的优化问题。自从Rohn[1]于2004 年首次提出以来，此后便吸引大量的学者对其解的存在性理论、数值求解以其收敛性分析进行深入探究。目前已经提出许多的数值求解方法，例如光滑牛顿法[2]、符号标记法[3]、松弛的非线性PHSS 类迭代法[4]等。近几年一些学者将AVE的相关理论进行推广，将AVE 延伸至二阶锥的框架之下，提出二阶锥绝对值方程（SOCAVE）问题：

式中：A∈Rn×n，b∈Rn和表示二阶锥意义下的x 的绝对值(定义为x 与自身的若当乘积的二次方根)，x∈Kn。通常意义下的二阶锥Kn是若干个二阶锥的笛卡尔乘积:

式中：n1+n2+…+nr=n 且≤x1｝，‖·‖表示欧氏空间的2-范数，只考虑单个二阶锥的情形即r=1。由于笛卡尔乘积的性质，所有的分析同样适用于多个二阶锥的笛卡尔积的情形。

SOCAVE(1)对锥优化这个新领域起到极其重要的作用。目前国内的一些学者对SOCAVE(1)进行了相关研究，并提出很多求解SOCAVE(1)的数值方法。例如，Hu 等[5]提出求解SOCAVE(1)的广义牛顿法，并证明该算法在一定条件下是全局收敛且局部二次收敛的。Miao 等[6]提出求解SOCAVE(1)的光滑牛顿法，证明该算法在一定条件下是局部二次收敛的。Huang 等[7]提出求解SOCAVE(1)的一种改进SOR-like 方法，在一定条件下对该算法进行收敛性分析和误差估计。最后将该算法与二阶锥上GN[5]、NSOR[8]、NINA[9]等方法进行对比，证明了所提出的迭代算法是有效的。

Zhang 等[10]在Li 研究的修正广义牛顿迭代方法[11](MGNT)的启发下,结合two-sweep 迭代方法[12-13]和单位矩阵方程[6，14]的思想，提出了求解AVE 的改进twosweep 迭代方法(MTS),将所提出的方法与MGNT 方法[11]和SOR-like 方法[15]进行一些数值实验，实验证明该方法在迭代步长和耗时方面更为有优势。基于此，将Zhang 等[10]的思路更进一步地扩展到求解SOCAVE(1)中去，添加一个惯性项(可见文献[16])，提出了求解SOCAVE(1)的惯性two-sweep 迭代方法，将所提出的方法与GN 方法[5]和MSOR-like 方法[7]进行数值实验对比，最后数值实验证明所提出的方法可行且有效的。

其余部分组织如下：在第二节中，主要介绍本文研究内容所涉及的基础知识以及相关引理；在第三节中,我们提出了求解SOCAVE(1)的惯性two-sweep 迭代方法并分析了相应算法的收敛性；在第四节中，给出所有相关算法的数值实验结果；在第五节中，对本文的工作进行总结。

1 预备知识

在欧式空间Rn中，基于二阶锥Kn，定义一个欧式若当代数V：＝（Rn,〈·,·〉,o），其中“o”表示若当乘积的运算符号，对于任意两个向量x=（x1，x2）∈R×Rn-1和y=（y1，y2）∈R×Rn-1，它们的若当乘积定义为：

基于上述若当乘积的定义，可知该若当代数V 中存在的单位元e=（1，0，…，0）∈Rn，x2表示x 与自身的若当乘积，即x2=x o x，因此SOCAVE(1)中绝对值的定义为。对于任意向量x=（x1，x2）∈R×Rn-1，基于二阶锥Kn的谱分解具有如下形式：

式中：λ1（x），λ2（x）称为x 的特征值，为对应的特征向量，它们的具体表达式如下：

式中：i=1,2,ω∈Rn-1,为满足‖ω‖=1 的任意向量。这里称为若当框架且有。如果x2≠0，则该谱分解表达式是唯一的。

令x+表示为x 在二阶锥Kn上的投影，x-表示为-x 在二阶锥Kn的对偶锥（Kn）*上的投影，结合x的谱分解(2)，可知x=x+-x-，基于文献[9]，可知：

引理1[17]设矩阵A∈Rn×n是非奇异的，矩阵A的逆的二范数严格小于1，即‖A-1‖<1，则二阶锥上的绝对值方程(1)对任意b∈Rn具有唯一解。

引理2[18]令

引理3[19]设向量x=（x1，x2），y=（y1，y2）∈R×Rn-1，那么

2 二阶锥绝对值方程组的惯性two-sweep迭代法及其收敛性分析

在本节中，将重点讨论和介绍二阶锥绝对值方程组的惯性two-sweep 迭代法(ITSM) 及其收敛性分析。在此之前，首先回顾Zhang 等[18]的MTS 迭代法，该方法是结合two-sweep 迭代法和添加单位矩阵方程的思想，用于求解AVE。基于MTS 方法，我们在二阶锥的框架之下，通过添加惯性项a（xn-xn-1），将所要求解的二阶锥绝对值方程等价地转化为以下迭代形式:

为了确定迭代方法(8)的收敛性质，通过引入一个恒等式关系(Golub 和Varga[14])，将(8)转化为下列形式:

下面，假设x*是SOCAVE(1)的唯一解，其满足下列形式:

因此，在(10)的第一个等式减去(11)的第一个等式，同时在(10)的第二个等式减去(10)的第二个等式，可以得到

取(12)中第一个方程两侧的范数:

同样取(12)中第二个方程两侧的范数:

于是

用字母G 定义不等式右侧的矩阵

由此可知，若ρ（G）<1，则由迭代方程组(10)生成的迭代序列将收敛到(1)的唯一解x*。

定理1如果系数矩阵A∈Rn×n在SOCAVE(1)中满足‖A-1‖<1，其中包含的参数θ 满足以下不等式:

那么对于任意两个初始向量x(0)和x(1),ITSM 算法(10)生成的迭代序列收敛到(1)的唯一解x*。

3 数值实验

为说明二阶锥绝对值方程组惯性two-sweep 迭代法的有效性，给出了两个数值模拟例子将其与另外两种迭代算法即GN 方法[5]和MSOR-like 方法[7]进行对比。其中n 表示矩阵阶数,“CPU”表示平均运行时间,“IT” 表示迭代步骤的数量,“ERR” 表示误差且ERR:=‖x(k)-x*‖(x*是精确解)，用“RES”表示绝对残差向量的范数，短条形符号“—”表示相应的最佳参数不存在。在我们的数值实验中，选取零向量为迭代初始向量，选择作为迭代的终止条件，最大迭代次数不超过1000。

此外，MSOR-like 方法中的ω 和a 满足:

例1[7]假设SOCAVE(1)中的系数矩阵A 和常数项b 是如下形式:

其中：x*=（-1,1,-1，1，…,-1,1）∈Rn。

在这个实验中，考虑单个二阶锥的情形即r=1，其中在MSOR-like 和ITSM 方法中满足‖A-1‖<1 这样的假设。首先，我们比较了文献[5]中的GN 方法、文献[7]中的MSOR-like 方法和ITSM 方法的数值性能，表1 列出了相应的数值结果。从表1 可以看出，所有提到的方法都可以近似求解SOCAVE。从表1 中，我们发现MSOR-like 方法和ITSM 方法的CPU 所占用的时间要远小于GN 方法。虽然GN 方法需要更多的CPU时间，但GN 方法得到的解更加精确。此外，我们发现ITSM 迭代方法不仅在迭代步数上低于MSOR-like 方法，而且在CPU 所占用的时间上要少于GN 方法和MSOR-like 方法。

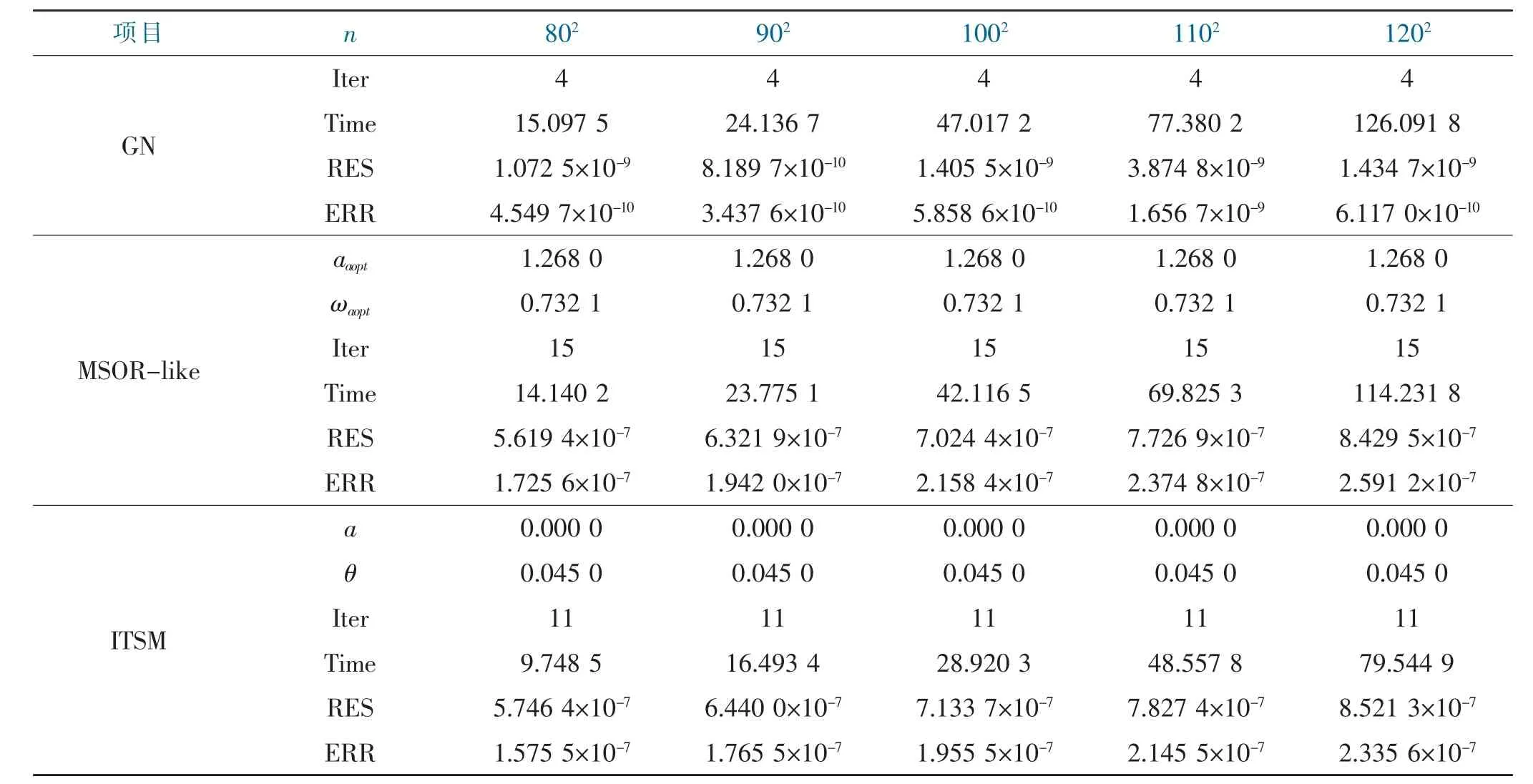
表1 GN、MSOR-like、ITSM 的比较Tab.1 Comparison between GN、MSOR-like and ITSM

例2[7]假设SOCAVE(1)中的系数矩阵常数项且b∈Rn，m 为规定的正整数且n=m2，其中:

在这个例子中，我们选择K=Kn作为二阶锥。GN方法、MSOR-like 方法和ITSM 方法这三种方法对于不同维数n 都可以有效且精确地求解。从表2 可知，GN 方法的精度都远高于其他两种方法。MSOR-like方法的精度几乎与ITSM 方法相同，但ITSM 在迭代步数和CPU 时间上都要优于MSOR-like 方法。表2 还表示，随着n=m2的增加，MSOR-like 方法的迭代次数和CPU 时间也在增加。

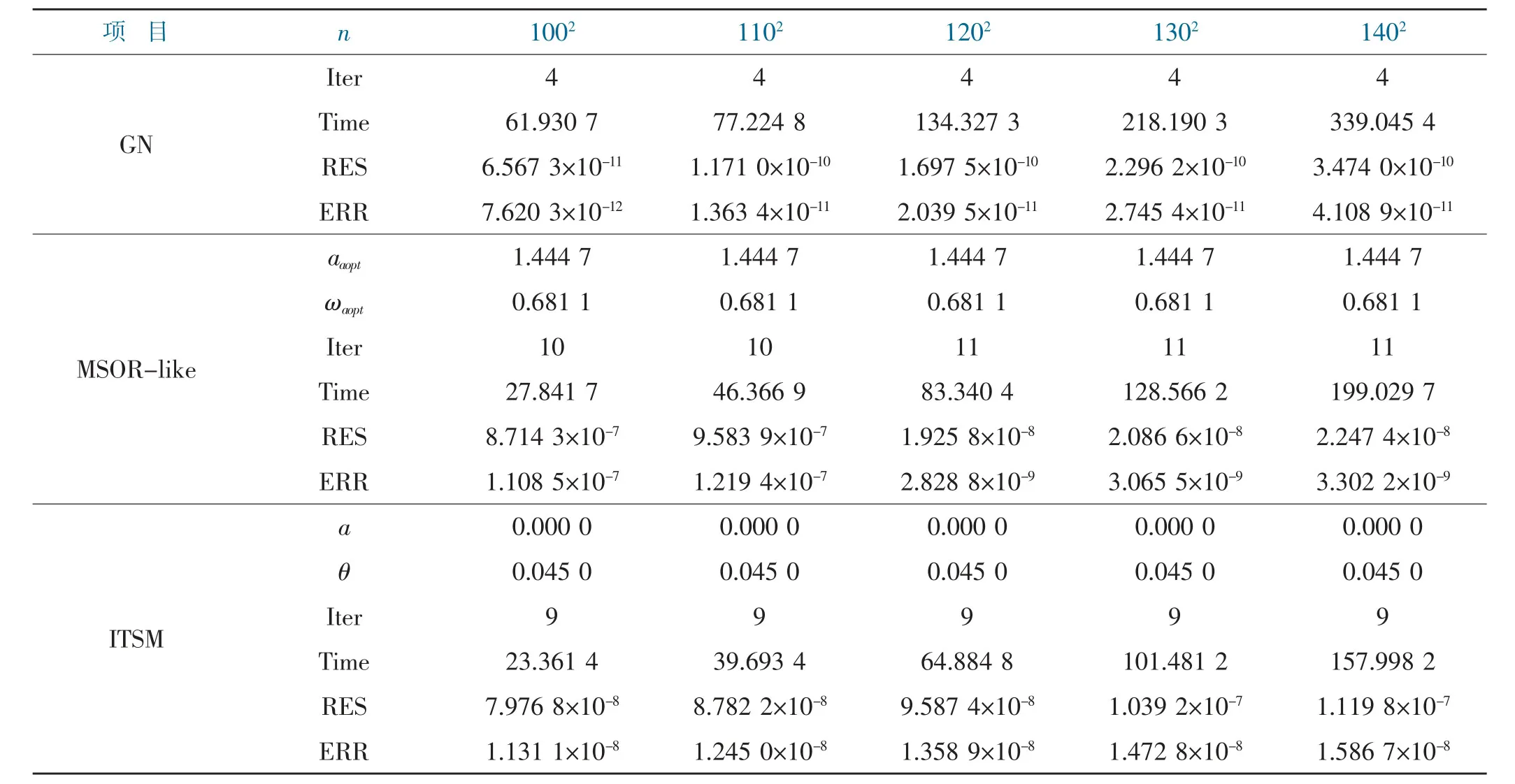
表2 GN、MSOR-like、ITSM 精度比较Tab.2 Comparison of accuracy between GN、MSOR-like and ITSM

4 结论

在二阶锥的框架之下引入一个惯性项和一个恒等式，提出了一种求解SOCAVE(1)的惯性two-sweep迭代方法，研究了该方法的收敛性，在适当条件下给出了保证该方法收敛的充分条件。数值结果表明该方法在迭代步数和CPU 时间方面均优于现有的方法。