药型罩形位偏差对聚能装药射流成型及其破甲过程影响

徐恒威，梁 斌，刘俊新，卢永刚，李军润，廖文军

（1.西南科技大学土木工程与建筑学院，四川 绵阳 621010； 2.中国工程物理研究院总体工程研究所，四川 绵阳 621900）

0 引 言

聚能装药利用炸药的爆炸化学能驱动药型罩沿中心轴线闭合形成高速射流，从而实现对坚固目标物的高效毁伤。聚能装药结构若想产生同轴、连续和准直的射流，就必须保持药型罩轴线与药柱轴线完全同轴，轴对称性是聚能装药发挥稳定破甲性能的重要保障［1］，基于现有的工艺水准，药型罩装配过程中总是会存在一定的宏观偏差［2］，导致药型罩轴线与药柱轴线不同轴，进而影响聚能战斗部的打击精度和毁伤效能。鉴于此，开展药型罩形位偏差对聚能装药射流成型及其破甲过程影响研究，对高效毁伤破甲弹药的研制及毁伤效应评估工作具有一定的参考价值。

聂源等［3］探究了起爆位置偏差、药型罩位置偏差、壁厚偏差与多宏观偏差耦合下射流横向位移的变化规律，获得了聚能装药制造过程中允许的单一宏观偏差允许范围。Coppinger 等［4］基于ALEGRA 软件研 究了药型罩密度、装药密度以及药型罩材料力学性能对射流横向偏移的影响规律，结果表明药型罩的密度变化会使射流产生大量的横向偏移。岳继伟等［5］针对含隔板聚能装药的起爆偏心效应展开了研究，证实隔板对起爆偏心效应的确具有放大作用，且该放大作用随起爆位置偏心量的增加而增大，但缺乏非对称射流侵彻特性的研究。刘健峰等［6］基于弹道试验研究了起爆偏心情形下弹丸的飞行特性及终点毁伤效应，认为EFP 战斗部的相对偏心量应该控制在3.3%以内。赵方宣等［7］、薛伟等［8］等通过LS-DYNA 非线性有限元软件模拟了壳体不对称情形下射流/弹丸的成型过程，基于现场试验结果讨论了非理想射流/弹丸毁伤效能的变化规律。综合以上成果可知，聚能装药非对称性影响因素的研究多集中在起爆偏心、壳体厚度不对称和药型罩加工质量等方面，有关药型罩形位偏差的研究较为少见，且制造偏差因素对射流侵彻过程及其侵彻特性的影响机理有待深入研究。

鉴于此，本研究针对聚能装药制造过程中常见的药型罩形位偏差展开试验研究，采用有限元软件LS-DYNA 对非轴对称情形下射流成型及其侵彻过程进行了数值模拟，揭示了药型罩偏移对压垮过程各时期影响的显著性差异，建立了药型罩偏移量与射流侵彻特性的关联关系，并探究了药型罩偏移与偏斜耦合下射流横向速度及弯曲程度的变化规律。

1 数值模拟

1.1 数值模型建立

常见的药型罩形位偏差分为3 种：a.药型罩偏移：药型罩轴线与药柱轴线存在水平偏移量；b.药型罩偏斜：药型罩轴线与药柱轴线存在偏斜角；c.药型罩偏移与偏斜耦合：药型罩轴线与药柱轴线既存在水平偏移量又存在偏斜角。具体特征如图1 所示，Δx表示药型罩偏移量，Δθ表示药型罩偏斜角；其中，药型罩向右侧偏移为正，药型罩顺时针偏斜为正。在工程实践中，图1a 和图1c 展示的情况最为常见［2］，因此，将针对这2 种情况开展研究。

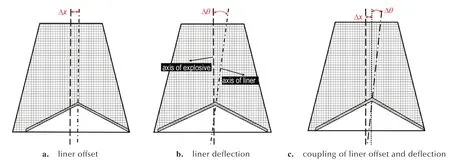
图1 药型罩形位偏差示意图Fig.1 Schematic diagram of shape and position deviation of liner

采用非线性有限元程序LS-DYNA 建立药型罩偏移情形下聚能装药侵彻坚固目标物的数值模型，模型由空气、炸药、药型罩及靶板4 部分组成，如图2 所示。空气、炸药、药型罩定义为Euler 共节点网格，靶板定义为Lagrange 网格，整个数值模型采用ALE 算法，Lagrange 网格与Euler 网格间用关键词*CONSTRAINED_ LAGRANGE_ IN_SOLID 进行耦合。

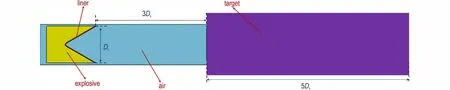
图2 聚能装药侵彻靶板数值模型Fig.2 Numerical model of shaped charge penetrating target

为使研究结果更具普适性，对聚能装药的结构参数进行无量纲化处理。其中，Dk表示聚能装药口径，罩顶装药高度取0.5Dk，药型罩壁厚取0.02Dk，罩顶圆弧半径取0.0375Dk，药型罩偏移量取0.025Dk，药型罩锥角为2α。网格排列采用渐变形式，药型罩母线方向上网格尺寸控制在0.25 mm，药型罩厚度方向上网格划分数量为4。起爆方式采用药柱上表面单点中心起爆。

1.2 材料模型及相关参数

空气采用空白材料模型（MAT_NULL）以及线性多项式方程共同描述［9］；炸药选用8701 炸药，以LS-DYNA软件中的高能炸药模型（MAT_HIGH_EXPLOSIVE_BURN）和JWL 状态方程进行描述［9］；药型罩材料是紫铜，密度为8.96 g·cm-3，其本构模型采用STEINBERG 模型［9］；靶板材料选用45#钢，密度为7.83 g·cm-3，运用JOHNSON-COOK 材料模型和GRUNEISEN 状态方程共同描述靶板的响应过程［9］。材料及状态方程参数均取自文献［9］，仿真模型单位制为cm-g-μs。

1.3 数值模型验证

1.3.1 脉冲X 光摄影及静破甲试验布置

为验证模型建立和材料参数设定的正确性，对药型罩偏移量（Δx）为0.025Dk时聚能装药射流成型及其侵彻过程展开了试验研究。图3 为聚能装药实物图，装药为8701 炸药，药型罩材料为紫铜；考虑到壳体材料（尼龙）阻抗较低且对爆轰波传播过程无影响，故可视作无壳聚能装药进行数值模拟计算。

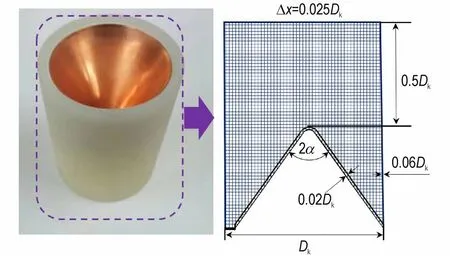
图3 聚能装药实物图Fig.3 Picture of shaped charge

采用ScandiFlash300 脉冲摄影装置对聚能装药射流成型过程进行拍摄，试验现场布置如图4 所示。试验前用铁丝将聚能装药垂直悬挂在脉冲X 光出光口和底片之间，并合理调整悬挂高度以确保底片能完整地捕捉到射流形态。装药起爆的同时开启计时系统，通过设置不同的出光时间以获得不同时刻下的射流形态。

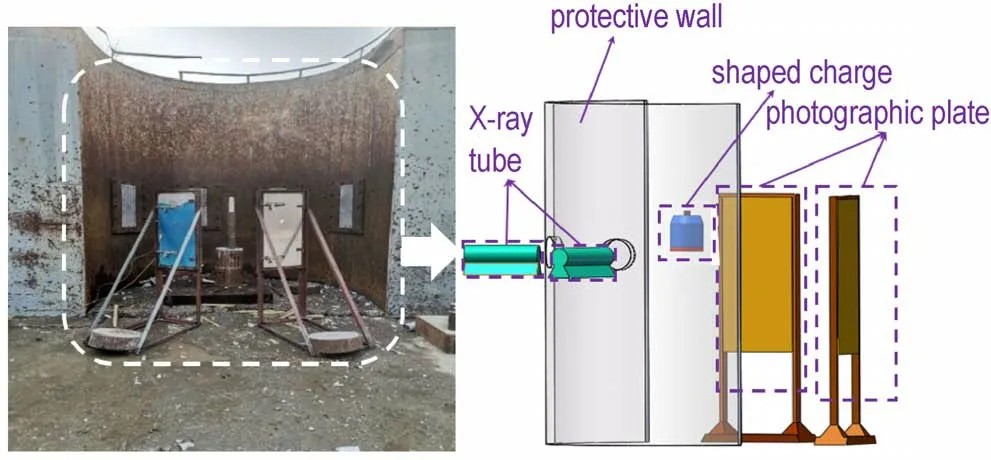
图4 脉冲X 光摄影试验布置图Fig.4 Layout of pulsed X-ray photography experiment

图5 为静破甲试验现场布置示意图。如图5 所示，开展静破甲试验需要的试验用品有：靶板、聚能装药、炸高筒、雷管、扩爆药。靶板材料为45#钢，炸高筒高度为3Dk。起爆方式采用雷管中心起爆扩爆药，再由扩爆药起爆装药；试验结束后，用刚尺测量靶板的开坑直径，后再沿中心轴线剖开靶板便能获得聚能装药侵彻深度及孔道。

图5 静破甲试验布置图Fig.5 Layout of static penetration experiment

1.3.2 验证

将聚能装药射流成型及侵彻过程模拟结果与脉冲X 光摄影试验、静破甲试验的结果进行对比，得到了图6 及射流威力参量数值模拟与试验结果的对比表1。由图6 可以看出，聚能射流的仿真形态与其实际形态高度相似，且射流侵彻钢靶的开坑形状以及侵彻孔道形状也与试验结果吻合较好。根据表1 可知，射流头部、杵体轴向速度的数值模拟结果为6318 和675 m∙s-1，与现场试验结果分别相差-3.5% 和+3.2%；射流长度（L）、射流偏离轴线的最大距离（δmax）、侵彻深度（H）与试验实测值分别相差-2.5%，-10.9%，+8.9%，误差均保持在11%以内，表明数值模拟结果与试验结果吻合度较高。开坑直径相对于试验实测值的误差为-24%，分析认为：可能是由于非轴对称聚能装药的加工难度较大，导致实际的药型罩偏移量（Δx）大于0.025Dk，因而射流弯曲程度更大，该观点从δmax的大小关系中也可以得到证实，故实际的开坑直径较数值模拟结果更大。由此可见，采用数值模拟方法能够较为准确地还原非轴对称聚能装药射流成型及其侵彻过程。

表1 射流威力参量数值模拟与试验结果对比Table 1 Comparison between numerical simulation and experimental results of jet power parameters

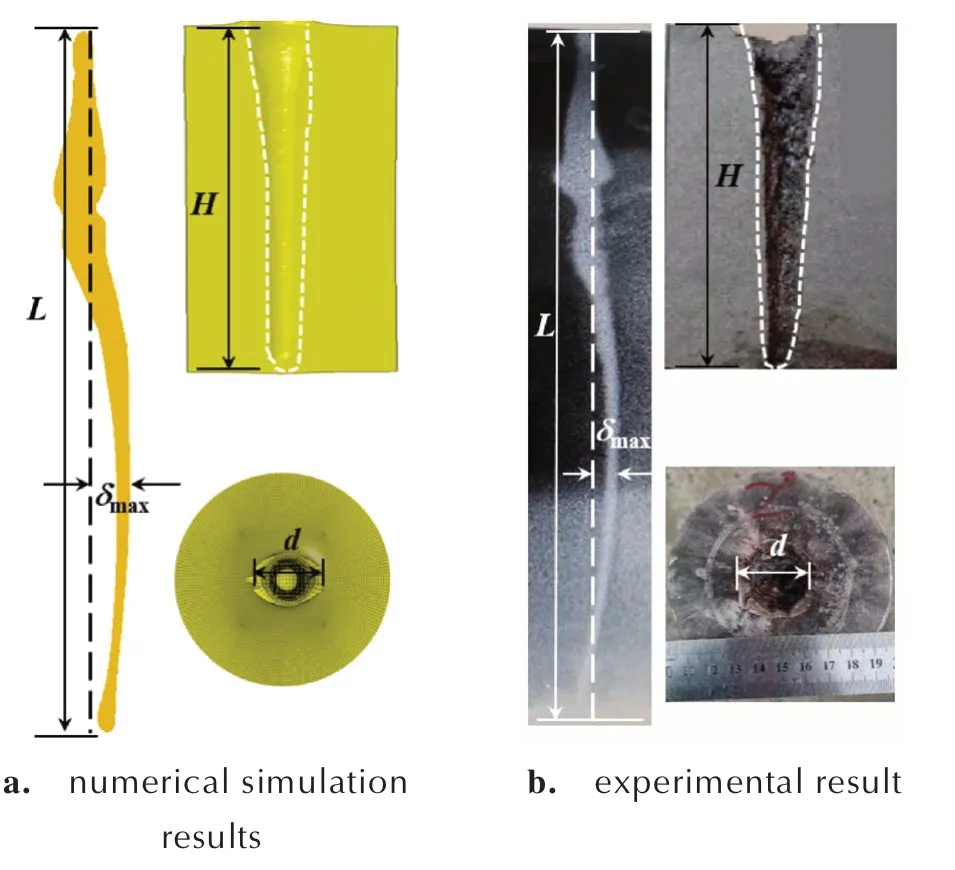
图6 数值模拟与试验结果对比Fig.6 Comparison between test and numerical simulation results

1.4 数值模拟

基于前文验证的模型创建及参数设定方法，分别建立药型罩偏移量（Δx）为0，0.0125，0.025，0.0375，0.05Dk下聚能装药侵彻钢靶的数值模型，所有数值模型除药型罩偏移量不同以外，其余结构参数与图2 完全一致。研究拟获得不同药型罩偏移量下罩表面压力分布、射流成型参数和威力参量。

1.5 示踪点技术

有限元分析软件LS-DYNA 支持定义示踪点输出流体单元的历史信息，内容包括坐标、速度和应力等信息，计算结束后信息会以固定格式保存至文件中，可用于获得射流成型过程中更多的细节信息［10］。示踪点分为动态示踪点和静态示踪点，动态示踪点跟随流体单元一起运动，静态示踪点则是固定位置。

研究在药型罩母线上均匀设置一定组数的静态示踪点，每组监测点关于药型罩轴线对称分布。爆轰波压垮药型罩的过程中，静态示踪点将会记录药型罩两侧微元的压力信息，待计算结束后，通过数据处理手段便能获得罩两侧爆轰压力差值的变化曲线。

2 仿真结果与分析

2.1 药型罩表面压力分布

为简化阐述过程，任意选取某一药型罩偏移量（Δx=0.025Dk）下的聚能装药结构为例，与轴对称聚能装药结构（Δx=0）进行对比分析，以说明药型罩偏移对罩表面压力对称分布的影响规律，图7 为起爆后不同时刻药型罩表面压力分布情况。

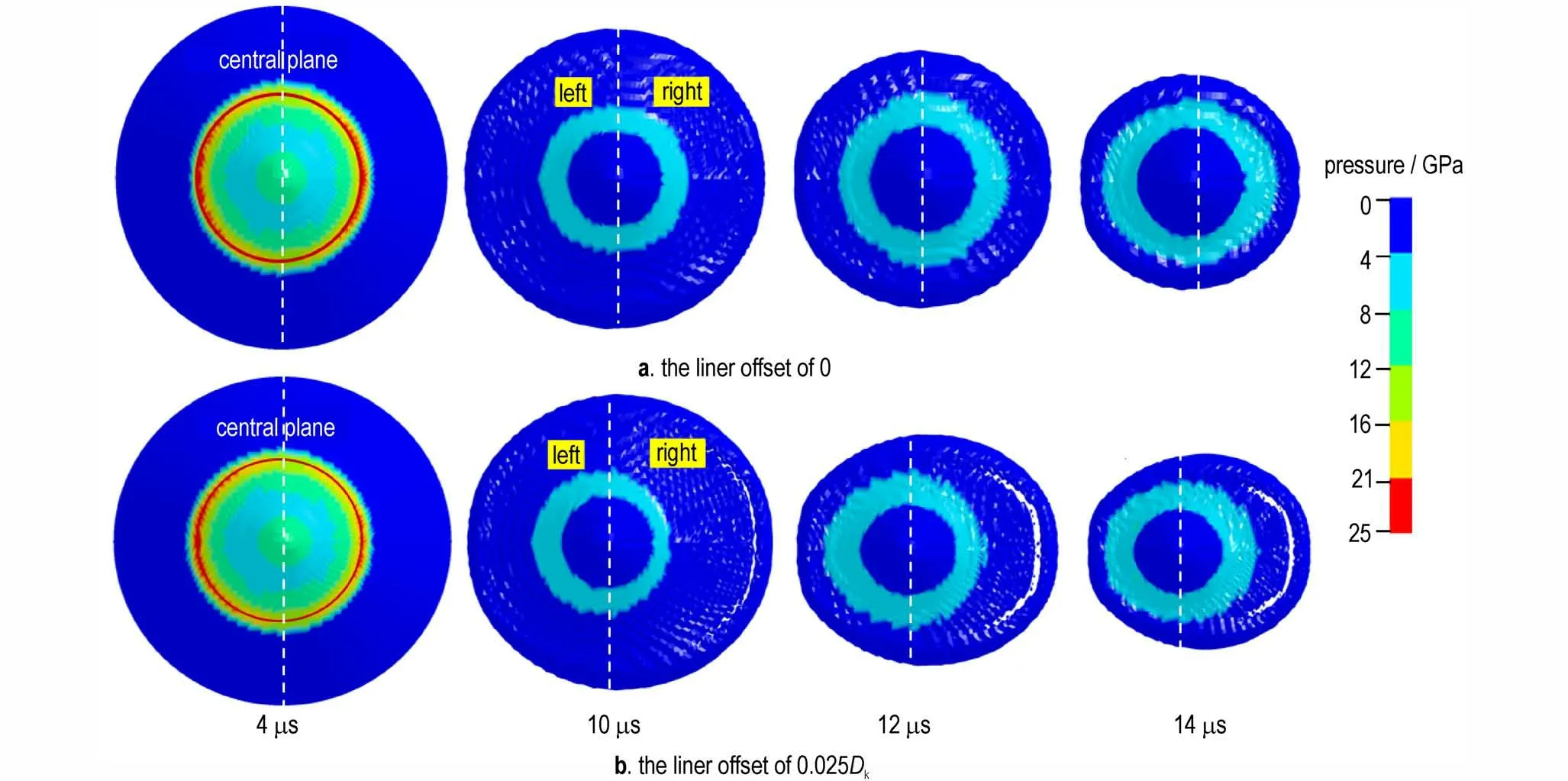
图7 药型罩表面压力云图Fig.7 Pressure distribution on the liner surface

由图7 可以看出，在压垮过程任意阶段（t=4，10，12，14 μs），轴对称聚能装药结构的药型罩表面压力均呈对称分布。对于药型罩偏移量（Δx）为0.025Dk的聚能装药结构，t=4 μs 时，中心面左侧的药型罩表面压力略大于右侧，但差异程度较小，总体可认为压垮过程早期药型罩表面压力呈对称分布；t=10，12 μs 时，爆轰压力在药型罩表面呈明显的非对称分布，中心面左侧的药型罩表面压力显著大于右侧，罩两侧轴对称位置处爆轰压力的差值最高能达到1.5 GPa；t=14 μs时，药型罩表面压力又基本恢复旋转对称分布。由此可见，药型罩偏移对罩表面压力对称分布的影响并非贯穿整个压垮过程，其主要影响压垮过程中期（t=10 μs）、中后期（t=14 μs），而压垮过程早期（t=4 μs）、后期（t=14 μs）近乎不受影响。

2.2 药型罩压垮过程

如图8 所示，t=4 μs 时，一部分爆轰波已达到药柱外表面边缘，意味着从此时开始，稀疏波将会陆续传入到爆轰产物中，使得爆轰压力下降［11］。图9 为罩两侧爆轰压力差值变化曲线，ΔZ表示静态示踪点距离药型罩顶部的垂直高度，Δp表示罩左侧微元与罩右侧微元表面爆轰压力的差值，该值可用于量化药型罩非对称压垮程度随偏移量（Δx）增加的演化规律。

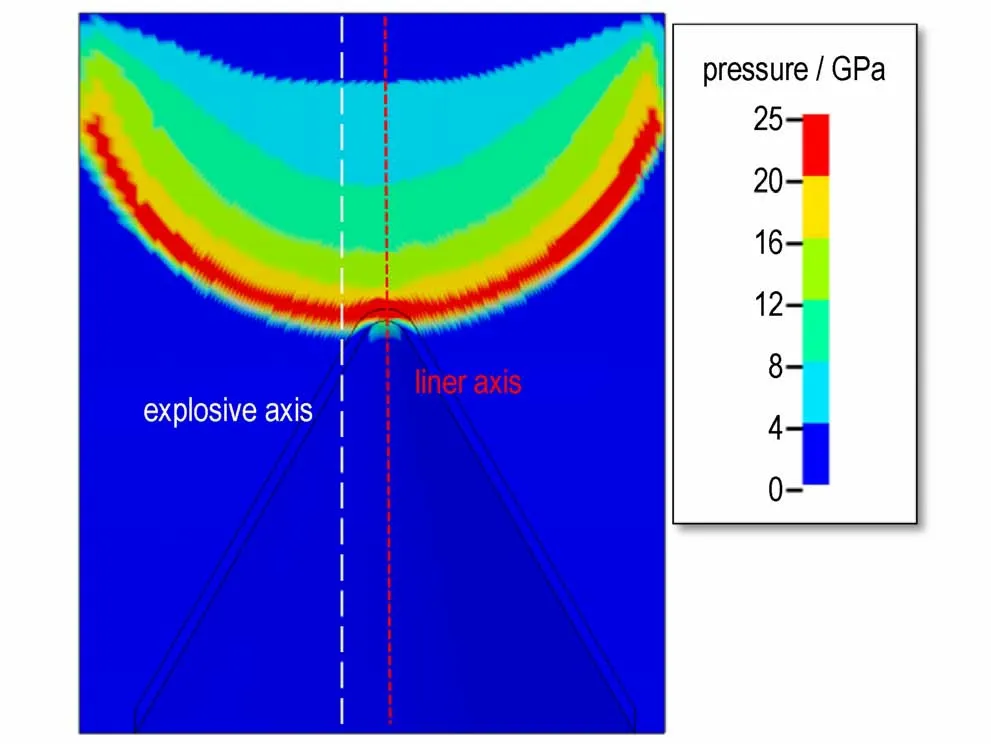
图8 爆轰波形（t=4 μs）Fig.8 Detonation waveform （t=4 μs）

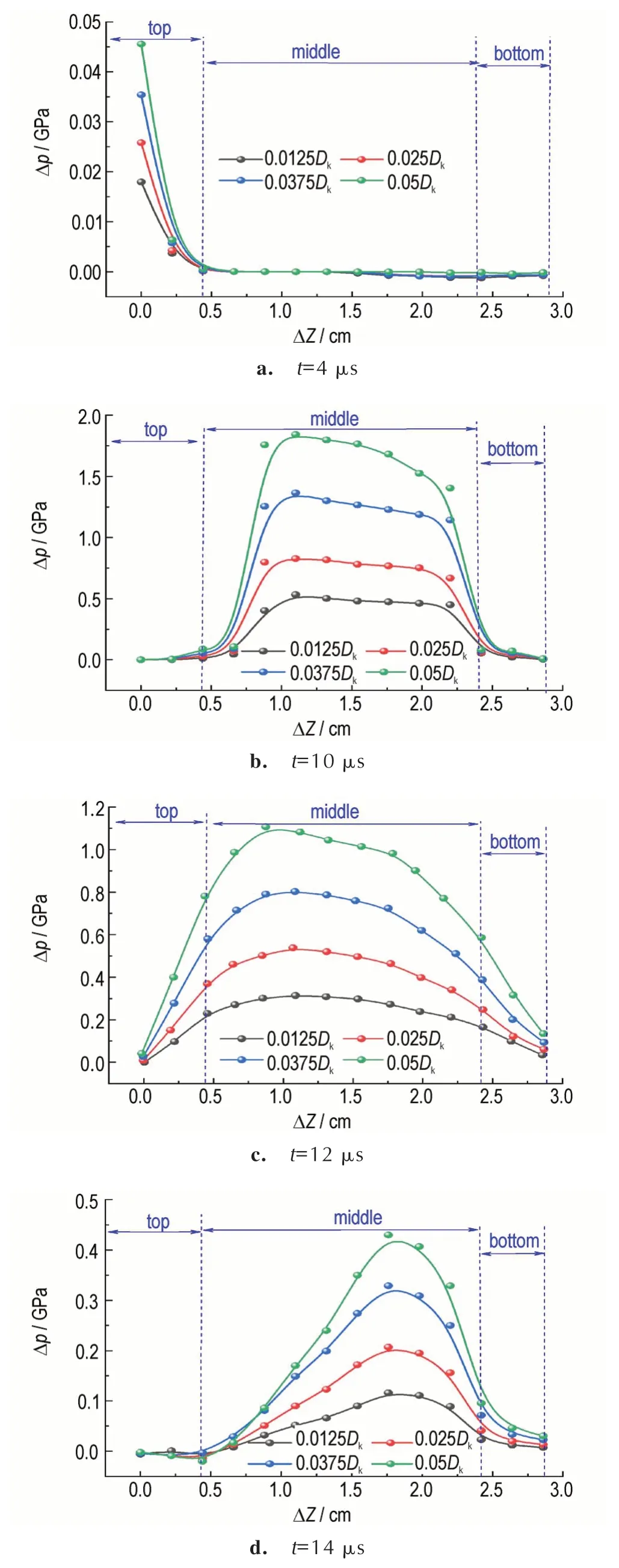
图9 罩两侧爆轰压力差值变化曲线Fig.9 Variation curve of detonation pressure difference on both sides of liner

如图9a 所示，t=4 us 时，由于药型罩向药柱轴线右侧偏移，所以稀疏波到达罩轴线右侧爆轰产物的时间领先于其到达左侧爆轰产物的时间，但此时只产生了少量稀疏波，故罩右侧爆轰压力有轻微下降，即罩左侧爆轰压力略大于右侧（0<Δp<0.05 GPa）；t=10 μs时，药型罩压垮过程进入中期阶段，爆轰波已完全传播至药柱外表面边缘，大量稀疏波会率先传入到罩右侧表面，且罩两侧炸药层厚度的差异也会导致炸药提供的爆轰压力不同，因此，此时的罩两侧爆轰压力差值（0.5<Δp<2 GPa）较t=4 μs 时显著增大，如图9b 所示；随着压垮过程继续进行，t=12 μs 时，稀疏波也陆续到达药型罩左侧表面，其传入时间的差异对罩两侧爆轰压力的影响已经消失，但罩两侧炸药层厚度的不同仍然会对爆轰压力造成影响，故罩两侧爆轰压力的不对称程度（0.2<Δp<1.1 GPa）较t=10 μs 时有所下降，如图9c 所示；当爆轰波向药型罩底部趋近时，装药对罩微元的驱动作用逐渐减弱，则罩两侧爆轰压力差值也随之降低（0.1<Δp<0.4 GPa），如图9d 所示。

由上述分析可知，药型罩偏移造成罩两侧稀疏波传入时间及炸药层厚度存在差异，具体表现为罩两侧爆轰压力呈非对称分布，从而导致爆轰压力对药型罩的非对称压垮作用。随着时间的增加，药型罩非对称压垮程度呈先增后减的趋势变化，在t=10 μs 时（中期阶段），药型罩非对称压垮程度达到最大。

2.3 射流形态及其成型参数

图10 展示了起爆后25 μs 时刻，不同药型罩偏移量（Δx）下射流形态及横向速度分布。当Δx=0 时，射流与药型罩轴线完全同轴；当Δx=0.0125Dk时，射流中段出现轻微弯曲，偏离轴线的最大距离（δmax）为0.035Dk，可认为射流还保持着良好的同轴性和准直性［2］；当Δx>0.0125Dk时，射流中部弯曲程度不断增大且多处出现断裂。由2.2 节可知，药型罩非对称压垮程度在中期阶段达到最大，而该阶段主要是形成射流中部，故射流中部横向速度最大，从而导致极易发生断裂。

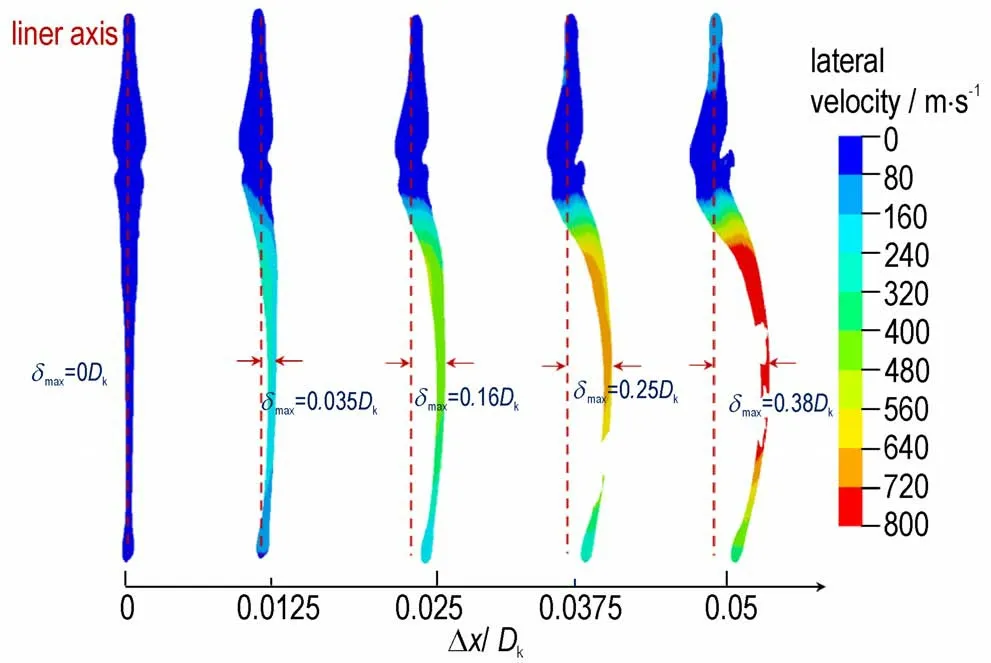
图10 t=25 μs 时，不同药型罩偏移量下射流形态Fig.10 Jet shape under different liner offset at t=25 μs

图11 为t=25 μs 时，射流成型参数演化曲线。由图11a 可知，随着药型罩偏移量（Δx）的增加，射流头部轴向速度和头尾轴向速度差先迅速下降，在偏移量（Δx）达到0.025Dk后下降趋势趋于平缓。在炸高固定的情况下，头尾速度差越大越利于射流在运动过程中沿轴线拉长。因此，在药型罩偏移量（Δx）为0～0.05Dk范围内时，射流长度呈先快速下降后平稳减小的趋势变化，如图11b 所示。

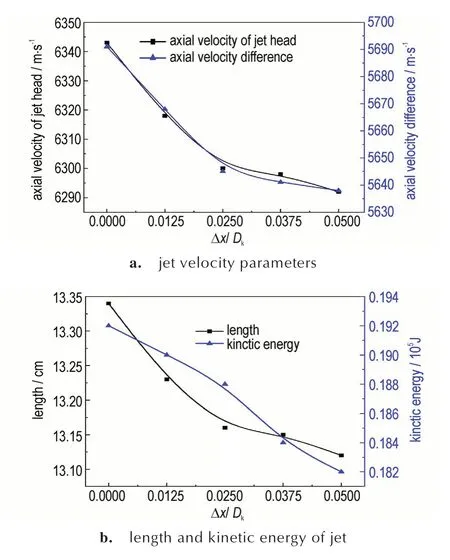
图11 t=25 μs 时，射流成型参数变化曲线Fig.11 Curve of jet forming parameters at t=25 μs

聚能装药是利用空穴效应将爆轰能量沿轴向汇集并转化为侵彻体动能的一种战斗部形式，则侵彻体轴向动能的大小直接决定了聚能装药战斗部的破甲性能［12］。随着药型罩偏移量（Δx）的增加，射流动能逐渐减小（图11b），另外，考虑到横向动能呈上升的趋势变化，意味着药型罩偏移量（Δx）的增加进一步降低了轴向动能，从而导致聚能装药破甲性能下降。

2.4 侵彻过程

药型罩偏移量（Δx）为0.025Dk时，聚能装药侵彻靶板的全过程，如图12 所示。t=25 μs 时，射流已经到达靶板上表面，横向速度的存在导致射流的开坑位置偏离轴线；t=45 μs 时，射流中后段进入靶板内部，由于该部分射流的弯曲程度较大，则会与靶板内壁发生相互作用，即增大了射流动能的损耗［14］；起爆后65 μs 时刻，射流中后段在靶板轴线右侧进行了二次开坑，形成了偏移侵彻孔道；t=90 μs 时，射流与杵体相互分离，偏移侵彻孔道与初始侵彻孔道完成相接，大量射流残渣堆积在靶板内部；t=110 μs 时刻，射流速度已经很低，导致后续难以推开靶板内的残渣［13］，影响了侵彻过程的进行，最终测得侵彻深度为14.46 cm。

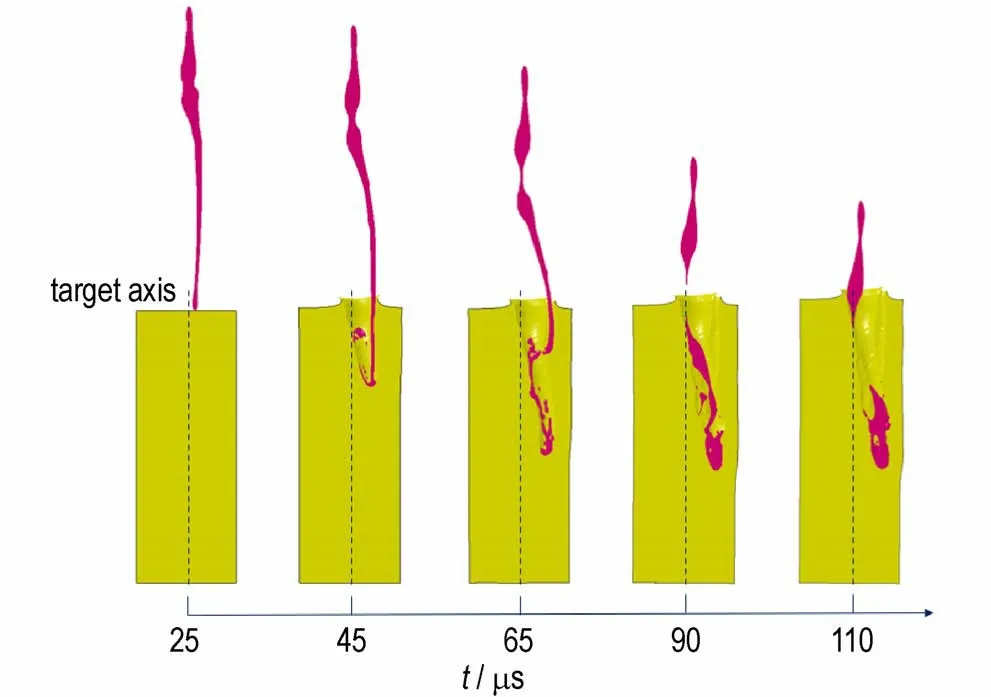
图12 Δx=0.025Dk时，射流对靶板的侵彻过程Fig.12 Penetration process of jet into the target plate at Δx=0.025Dk

2.5 开坑形状及侵彻深度

药型罩偏移量（Δx）为0，0.025，0.05Dk时，靶板开坑形状如图13 所示。药型罩偏移量（Δx）为0 时，射流保持着良好的线性特征且与中心轴线完全同轴，故开坑形状呈旋转对称状，如图13a 所示；随着药型罩偏移量（Δx）增加，射流形态逐渐弯曲，当头部侵彻开坑结束后，待横向速度更大的中后段到达靶板上表面时，由于其积累的横向位移大于初始侵彻孔道的孔径，则该部分射流将在靶板上进行二次开坑，导致后续射流无法直接作用于孔底以增加侵彻深度［14］，形成了图13b与图13c 所示的偏移侵彻孔道。药型罩偏移量（Δx）越大则意味着偏移侵彻孔道的孔径越大，表明有更多的射流动能损耗在形成偏移孔道上，从而出现大开孔低侵深的现象。

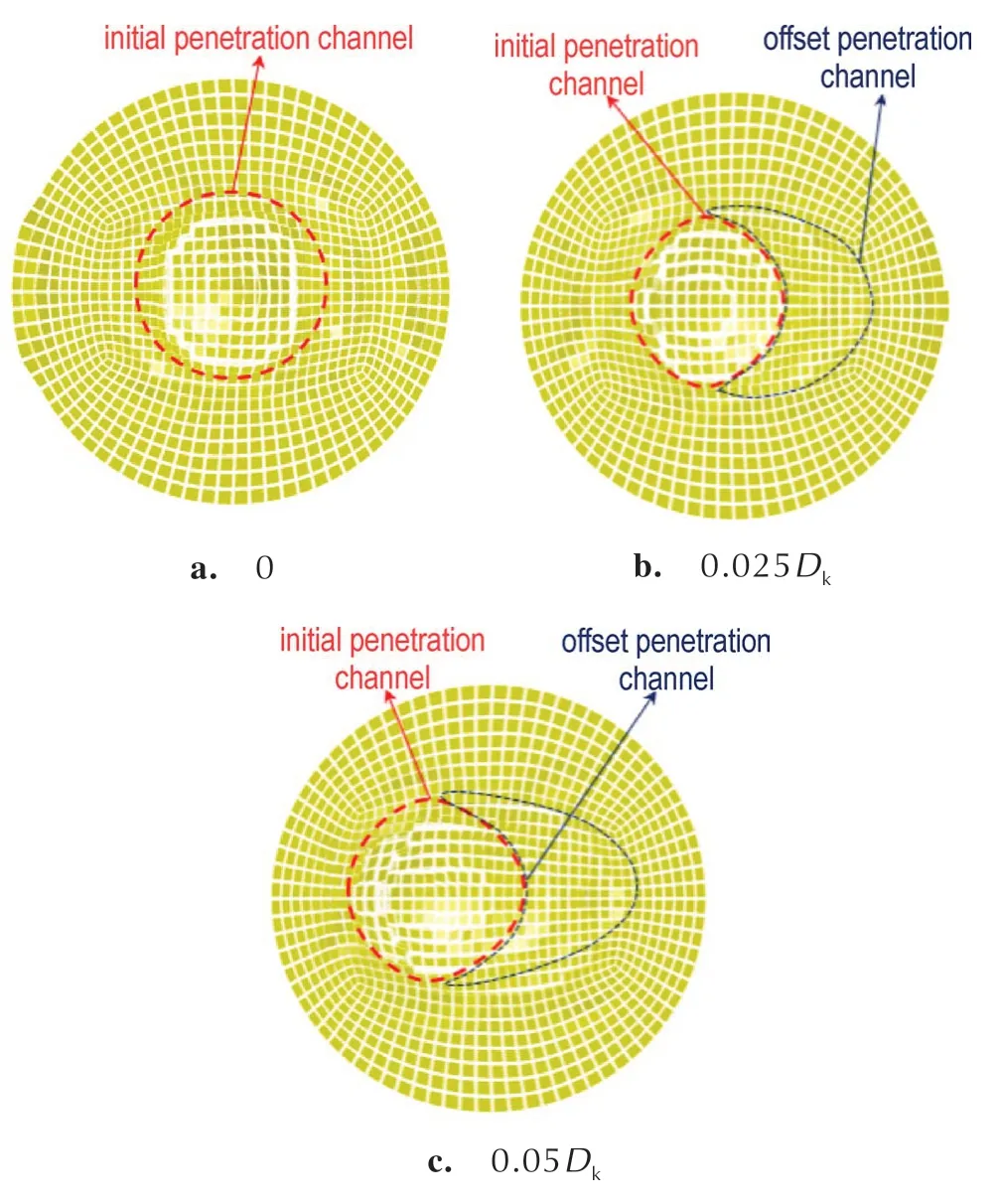
图13 靶板开坑形状Fig.13 Penetration channel of target

表2 给出了不同药型罩偏移量（Δx）下聚能装药侵彻深度的计算结果。与轴对称聚能装药结构相比，药型罩偏移量（Δx）为0.0125Dk时聚能装药的侵彻深度下降了6.6%；当药型罩偏移量（Δx）为0.025Dk时，侵彻深度下降了11.1%，这已经超过正常的穿深跳动范围（10%）；随着药型罩偏移量（Δx）的增加，射流侵彻深度继续下降，当药型罩偏移量（Δx）为0.05Dk时侵彻深度下降百分比高达32.5%。由此可见，为提高聚能战斗部的破甲稳定性，应将药型罩偏移量（Δx）控制在±0.0125Dk范围内。

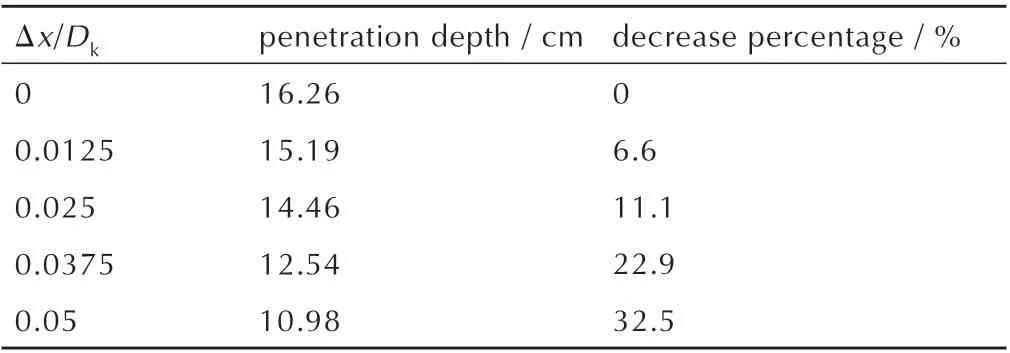
表2 不同药型罩偏移量（Δx）下侵彻深度计算结果Table 2 Calculation results of penetration depth under different offsets（Δx）

3 药型罩偏移与偏斜耦合下聚能装药射流成型过程

前文针对药型罩偏移的情况展开了系统性研究，但在实际工程中药型罩偏移与偏斜耦合的情况也频繁出现，然而相关研究鲜有公开报道，两者间的关联关系也不得而知。鉴于此，根据表3 设计的数值模拟方案，对药型罩偏移与偏斜耦合下聚能装药射流成型过程开展了三维数值模拟研究，结果如图14 和图15 所示。

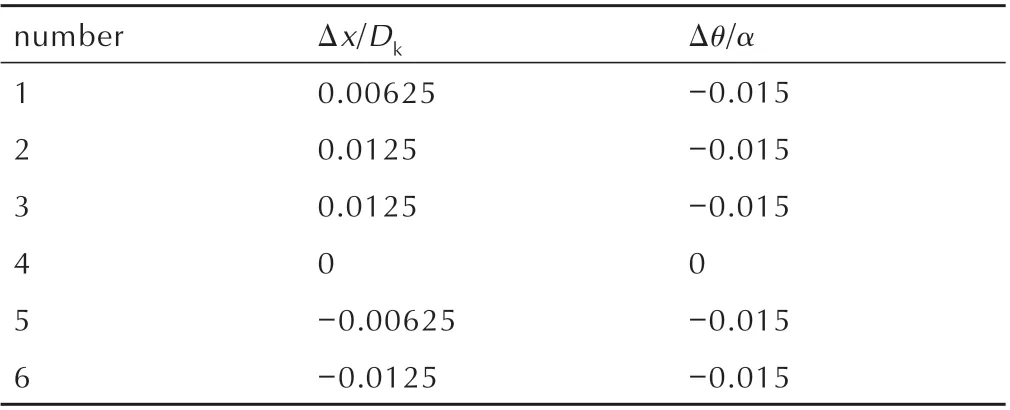
表3 数值模拟方案Table 3 Numerical simulation scheme

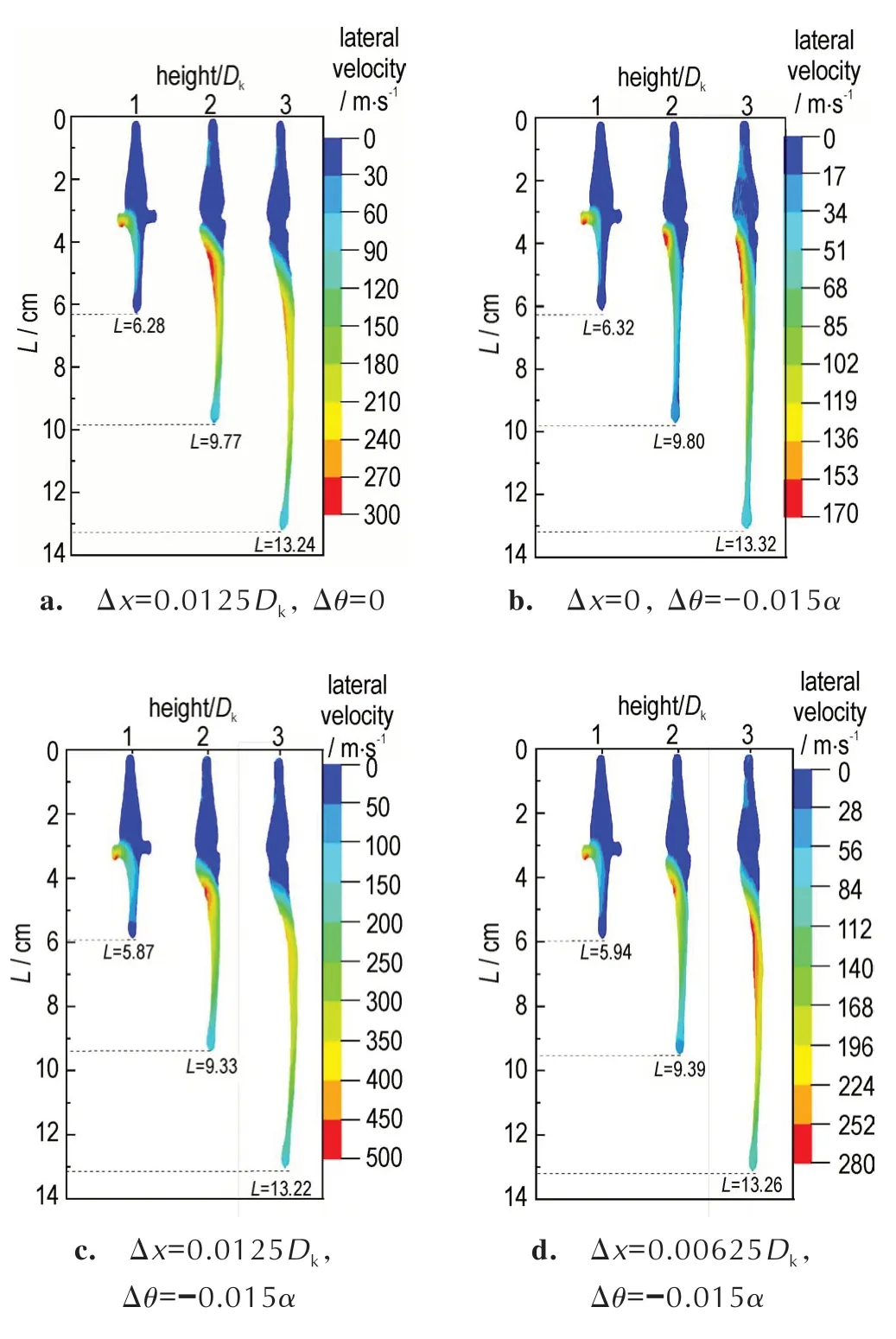
图14 药型罩偏移与偏斜反方向耦合Fig.14 Coupling of liner offset and deflection in the opposite direction

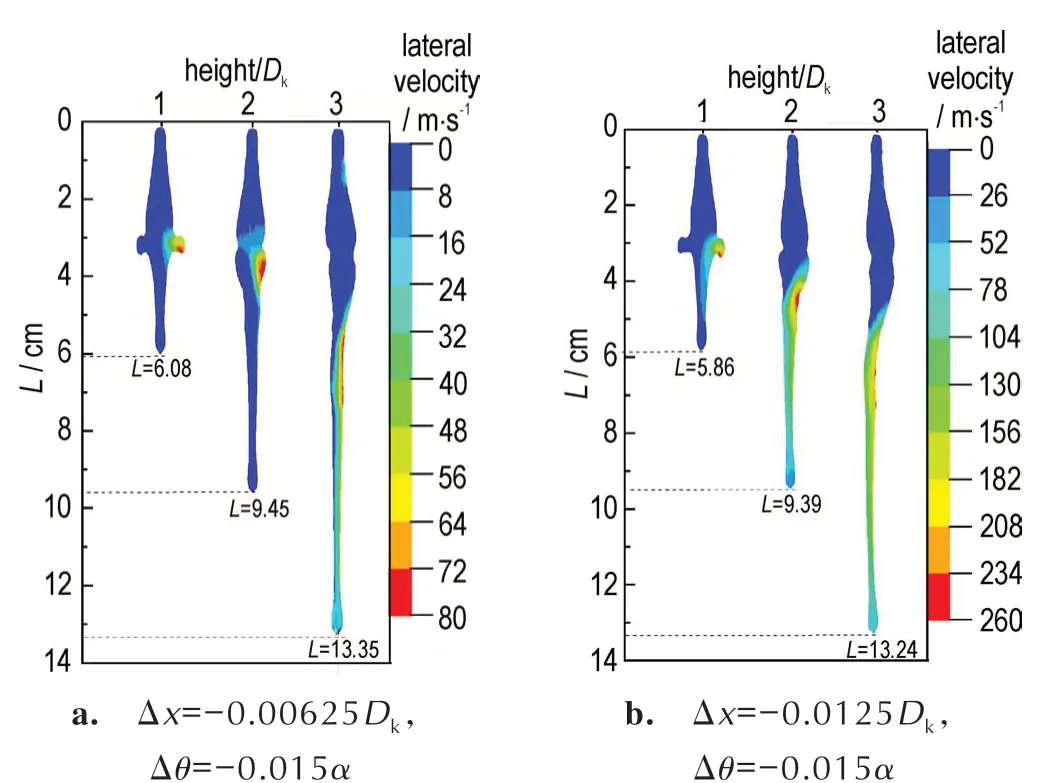
图15 药型罩偏移与偏斜同方向耦合Fig.15 Coupling of liner offset and deflection in the same direction

图14 为药型罩偏移与偏斜反方向耦合下射流形态及横向速度分布图。从图14a 和图14b 可以看出，药型罩偏移和药型罩偏斜情形下，射流横向速度最大值分别为170 m∙s-1和300 m∙s-1；但当药型罩偏移与偏斜反方向耦合时，横向速度最大值大于各单一偏差情形下的横向速度最大值之和，如图14c 所示，表明两者的耦合进一步加剧了射流的非对称程度，导致其具有更大的横向速度。再根据图14c 和图14d 可以看出，药型罩偏移与偏斜反方向耦合时，单一偏差的增加会驱使射流横向速度及弯曲程度呈增大的趋势变化。

当药型罩偏移与偏斜同方向耦合时，射流横向速度最大值仅为80 m∙s-1，如图15a 所示，可认为该情形下射流具有良好的准直性和对称性，这是由于此时药型罩偏移与偏斜引起的射流弯曲方向相反，因而两者的耦合相互抵消了对方对射流对称性造成的影响；如图15b 所示，随着药型罩向左偏移，射流弯曲方向发生改变，说明在该情形下的药型罩偏移与偏斜耦合中，药型罩偏移占据主导地位，其对射流形态的影响更为显著，故射流弯曲方向与药型罩偏移方向一致；若继续增大药型罩向左的偏移量（Δx），射流弯曲程度及横向速度应该往左持续增大。因此，药型罩偏移与偏斜耦合情形下，当某一因素保持不变时，另一因素存在最佳取值；小于该最佳取值时射流的不对称程度随该因素的增加而减小，大于时则随之增加而增大。

综上所述，药型罩偏移与偏斜反方向耦合时，两者的耦合将使得射流弯曲程度及横向速度更大；对应地，若是药型罩偏移与偏斜同方向耦合时，各单一因素引起的非对称参量会在射流成型过程中相互抵消，从而获得相对准直的射流。若已知某聚能装药结构的制造偏差因素，可通过调整各因素间的耦合关系以及控制主要因素来减小制造偏差对射流成型过程的影响，以期获得准直性好、连续性高的聚能射流，进而为解决聚能战斗部存在破甲稳定性不足的问题提供研究思路。

4 结 论

针对聚能装药制造过程中存在的药型罩形位偏差问题，基于经现场试验验证的数值模型，研究了药型罩偏移对聚能装药射流成型及其破甲过程的影响，并探究了药型罩偏移与偏斜耦合下射流形态及横向速度的变化规律，得到如下结论：

（1） 药型罩轴线与装药轴线存在水平偏移量时，爆轰波对药型罩压垮过程中期、中后期的非对称作用导致射流中后段具有较大的横向速度，宏观上表现为射流呈弓形弯曲状。

（2） 当药型罩偏移量在0～0.0125Dk范围内时，射流保持着良好的成型性能，头部轴向速度、头尾轴向速度差和长度随偏移量增加而急据下降；药型罩偏移量超过0.0125Dk时，射流形态严重弯曲且会出现断裂，但头部轴向速度、头尾轴向速度差和长度趋于平缓变化。

（3） 含药型罩形位偏差的聚能装药侵彻靶板时，横向速度较大的射流中后段将会在靶板上进行二次开坑，从而形成偏移侵彻孔道，虽增大了开坑直径，但降低了侵彻深度。为最大程度发挥聚能装药的侵彻性能，药型罩偏移量应控制在±0.0125Dk范围内。

（4） 药型罩偏移情形下，射流弯曲方向与药型罩偏移方向一致；药型罩偏斜情形下，射流向药型罩偏斜方向发生偏转。药型罩偏移与偏斜耦合时，射流的弯曲程度为各单一偏差因素引起的弯曲程度矢量叠加。