风力发电机复合材料叶片振动特性分析

张 政,王国伟,卢秉喜

(1. 甘肃重通成飞新材料有限公司,甘肃 武威 733000; 2. 兰州理工大学 机电工程学院,甘肃 兰州 730050)

纤维增强复合材料(Fiber reinforced plastics,FRP)具有比强度和比刚度高、抗疲劳性能和可设计性好等诸多优点,风力发电机叶片多用其铺层制造而成[1]。国内外广大学者对风力发电机复合材料叶片振动特性展开研究。其中国外学者根据几何精确梁模型对叶片模态进行数值计算,并将计算结果与有限元计算结果进行对比[2];建立叶片振动方程,提取其降阶模型,并将该降阶模型在稳态解附近线性化,得到叶片动态特性[3]。多体动力学作为动力学理论重要分支,近年来国内学者以多体动力学方法展开建立叶片结构动力学建模,将叶片划分为3～4个超级单元且每个超级单元间使用不同铰链接,围绕考虑动力刚化效应的模态频率、气弹频率、气弹稳定性等展开一系列研究[4-5]。

综上所述,国内外研究学者对叶片振动特性展开研究并取得显著成果。本文以NREL 5MW风力发电机复合材料叶片为研究对象,基于复合材料基础对叶片进行铺层,研究其静态固有频率及运行时固有频率。

1 理论简介

叶片固有频率分析通常采用有限单元法,惯性力与物体质量和加速度有关,作用在叶片总惯性力为[6]

(1)

其中

(2)

作用在叶片总阻尼为

(3)

其中

(4)

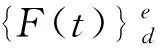
作用在叶片总弹性力为

(5)

其中

(6)

式中:[K]e为单元刚度矩阵;{F(t)}e为单元弹性力;{u(t)}为单元节点位移。

由达朗贝尔原理可知,任意时刻作用在叶片的力构成平衡力系,则

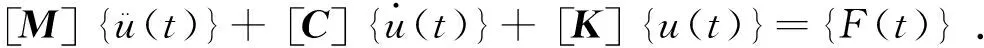
(7)

对于无阻尼自由振动,阻尼项和外载荷项均为零,因此式(7)变为

(8)

设式(8)解为

{u(t)}={X}sinωt,

(9)

式中:{X}为位移{u(t)}的振幅列向量;ω为自振频率。

将式(9)代入(8)中,可得

([K]-ω2{M}){X}=0 .

(10)

令ω2=λ,则

([K]-λ{M}){X}=0.

(11)

式(11)为齐次方程,要使其有非零解,矩阵([K]-λ{M})行列式应为零,即

det([K]-λ{X})=

(12)

式(12)为广义特征方程,若节点位移总自由度为n,即刚度矩阵[K]的阶数为n×n,由行列式展开可得,式(12)为λ的n次代数方程,由此可得n个广义特征值λi(i=1,2,3,…,n)。故叶片n阶固有频率为

(13)

2 叶片模型

2.1 叶片建模

本文以NREL 5 MW风力发电机组为研究对象,其基本参数见表1[7]。

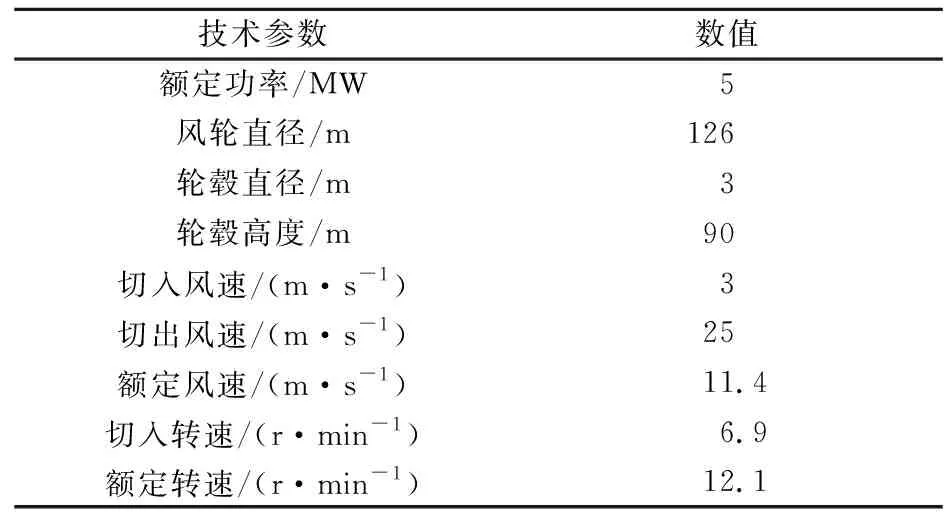
表1 NREL5 MW风力机主要参数

NREL 5 MW风力发电机叶片长度为61.5 m,最大弦长位于距叶根15.85 m,其值为4.652 m;且叶片腹板分别位于弦长15%和50%处,叶片最大扭角为13.308°。该叶片主要采用DU40_A17、DU35_A17、DU30_A17、DU25_A17、DU21_A17及NACA64_A17号翼型。在三维建模软件中对叶片翼型处理后,完成叶片壳体建模,如图1所示。

图1 叶片壳体模型

图1中叶片根部为圆截面,方便于轮毂进行连接;靠近叶根区域采用DU系列翼型,该翼型相对厚度为21%～40%,保证叶片根部具有足够刚度支撑,叶尖处采用NACA64_A7翼型,为叶片提供良好气动特性。

2.2 叶片结构网格划分

对复合材料叶片铺层前需对叶片进行结构网格划分。本研究通过有限元平台中复合材料铺层模块ACP(ANSYS Composite Prepost)实现对叶片复合材料铺层,叶片壳体模型选取SHELL181单元进行网格划分,该单元为4节点6自由度单元,可分析壳体结构。设定叶片表面网格尺寸为80 mm;最终网格正交质量为0.996 1,表明网格质量较好,满足有限元计算需求。得到离散化单元总数为114 538,总节点数为112 782。网格划分结果如图2所示。

图2 叶片结构网格划分

2.3 铺层设计

叶片铺层设计以复合材料各单向板力学性能为依据,对层合板结构进行铺层角度、铺设方向和铺设层数确定,同时须考虑叶片在实际工作中气动性能、不同部位所受载荷及经济要求。因此,叶片铺层设计时应不断进行迭代与优化,以保证叶片满足标准设计要求。叶片铺层材料力学性能参数见表2[8]。

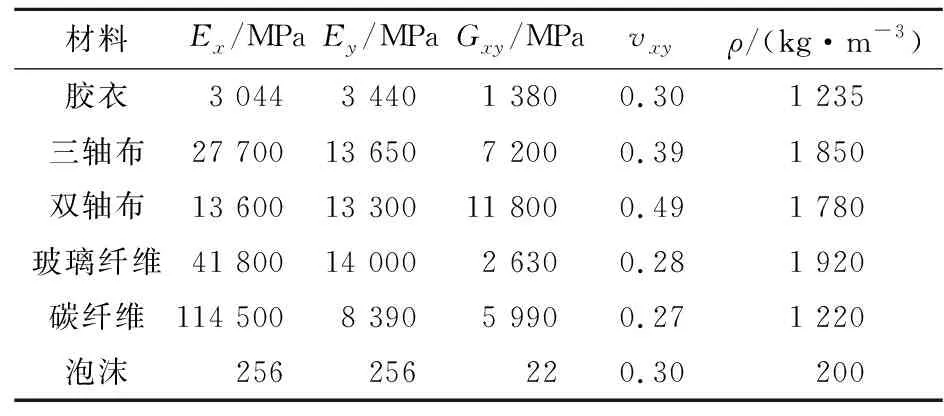
表2 叶片铺层材料力学性能参数

叶片剖面结构设计为叶片结构设计中不可或缺部分,其直接决定叶片结构性能。将叶片沿弦向分为主梁、前缘、尾缘、前缘镶板、尾缘镶板、尾缘加强,并沿叶片展向按照其翼型分布最终将叶片划分为240个区域,在每个区域对叶片铺层。根据德国劳氏船级社(GL)关于叶片的认证标准,初步确定本研究复合材料叶片铺层方案,叶片剖面铺层如图3所示。

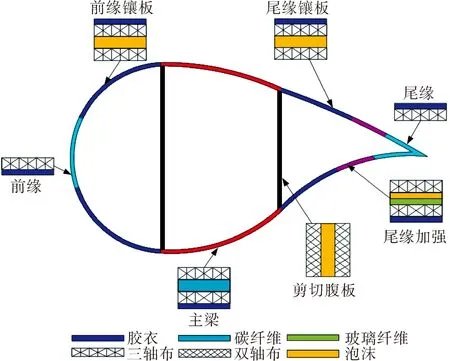
图3 叶片剖面铺层

叶片最外层选取胶衣为铺设材料,对叶片进行保护,避免其受到风沙、水汽等环境介质侵蚀;本文以强度最高的碳纤维作为主梁夹芯结构中间层,三轴布为夹芯结构两端。前缘镶板、尾缘镶板和剪切腹板结构是以泡沫填充物为中间层,双轴布为两端夹芯结构;前缘及尾缘分别采用三轴布为主要铺设材料的层合板结构;尾缘加强夹芯结构以玻璃钢和泡沫为中间层,两端为三轴布。叶片沿展向铺层材料及铺设层数如图4所示。

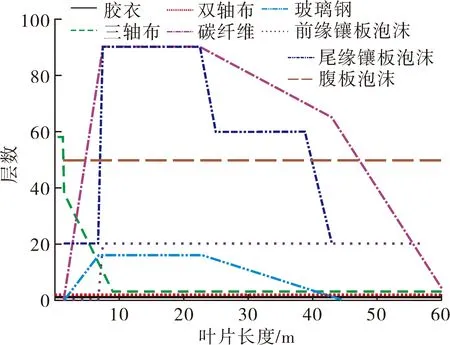
图4 叶片沿展向铺层材料层数

图4中,胶衣作为叶片外表面铺设材料,铺设层数为1层。双轴布作为腹板夹芯结构两端铺设材料,沿叶片展向其铺设层数保持为4层。三轴布铺设于主梁、前缘镶板、尾缘镶板、前缘、尾缘和尾缘加强处,其铺设层数沿叶片展向保持为4层。碳纤维作为主梁铺设材料,其铺设层数沿叶片展向为先增大后减小,距叶根7.5～22.5 m时达到最大为90层。玻璃纤维主要铺设于尾缘加强处,铺设最厚处为16层。尾缘镶板泡沫铺设层数为先增大后减小,从叶根开始到距离叶根7. 5 m处,其铺设层数为20层;距叶根7.5～22.5 m时,铺设层数为90层;之后铺设层数继续减小至20层。前缘镶板泡沫从距叶根7.5 m开始至57.4 m处,其铺设层数为20层;剪切腹板泡沫铺设层数保持不变为80层。整个叶片铺层厚度沿叶片展向先增大后减小。完成复合材料叶片铺层如图5所示。

图5中,整个叶片铺设厚度沿叶片展向为先增大后减小。叶片有限元模型其最厚处厚度为114.49 mm,位于尾缘镶板处;厚度最薄处位于叶尖,其厚度为3.81 mm;叶片整个尾缘处厚度均大于前缘厚度,且整个叶根处厚度保持不变,均为53 mm。

图5 叶片铺层

3 结果分析与讨论

3.1 模态分析

叶片在旋转过程中,固有频率与风轮激振频率接近,使得叶片发生强烈共振,影响风电发电机正常运行,甚至发生破坏。因此,非常有必要对叶片模态特征展开研究,采用Block Lanczos法求解模态。对叶根部分采用全固定约束,得到叶片前6阶固有频率及模态振型见表3。

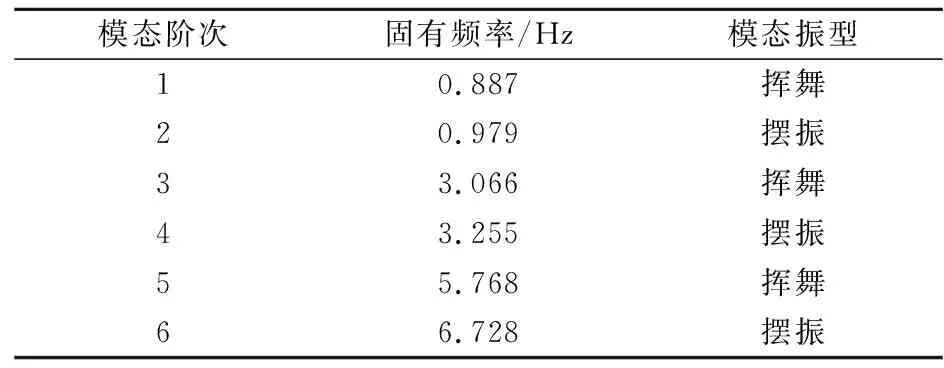
表3 叶片前6阶固有频率及振型

表3中,叶片低阶模态以挥舞和摆振方向振动为主;叶片前6阶模态中,第1阶、第3阶、第5阶模态为挥舞方向振动,第2阶、第4阶、第6阶模态为摆振方向振动;随着叶片模态阶数增加,其振动变形量也逐渐增大。叶片前6阶模态振型如图6所示。

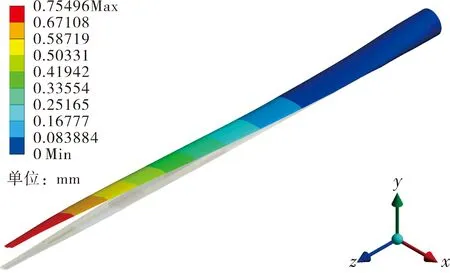
(a) 第1阶

(b) 第2阶

(c) 第3阶

(d) 第4阶

(e) 第5阶

图6中,叶片前6阶模态振型主要为第1阶挥舞、第1阶摆振、第2阶挥舞、第2阶摆振、第3阶挥舞和第3阶摆振。其中叶片第1阶挥舞频率为0.887 Hz,第1阶摆振频率为0.979 Hz,第2阶挥舞频率为3.066 Hz,第2阶摆振频率为3.255 Hz,第3阶挥舞模态频率为5.768 Hz,第3阶摆振模态频率为6.728 Hz。叶片前6阶模态主要为弯曲振动,即挥舞和摆振,故该叶片其主要振型为弯曲振动,并且其最大变形集中在叶尖处,扭转振动发生在更高阶,不是叶片主要振型。根据振动理论,叶片振动主要能量集中在低阶模态,且本研究中叶片前6阶模态均未出现扭转变形,说明该叶片实际抗扭转性能较强。

叶片在服役时受离心载荷作用,使得叶片振动频率发生变化。因此,有必要对旋转叶片展开动模态特性研究。首先基于预应力模态,在静力模块中对叶根处采用固定约束并设定叶片不同旋转速度,通过设置叶片绕Y轴旋转,求得不同旋转速度叶片所受离心力;然后在模态分析模块设定提取叶片模态阶数为6阶;最后采用Block Lanczos法求解叶片前6阶旋转频率。

考虑本研究叶片实际主要旋转速度区间为6.9～12.1 r/min,本节中以6.9 r/min为叶片动模态旋转速度起始转速,12.1 r/min为旋转速度区间终点,以1.04 r/min为增量,分别求取该区间不同转速叶片前6阶振动频率,见表4。

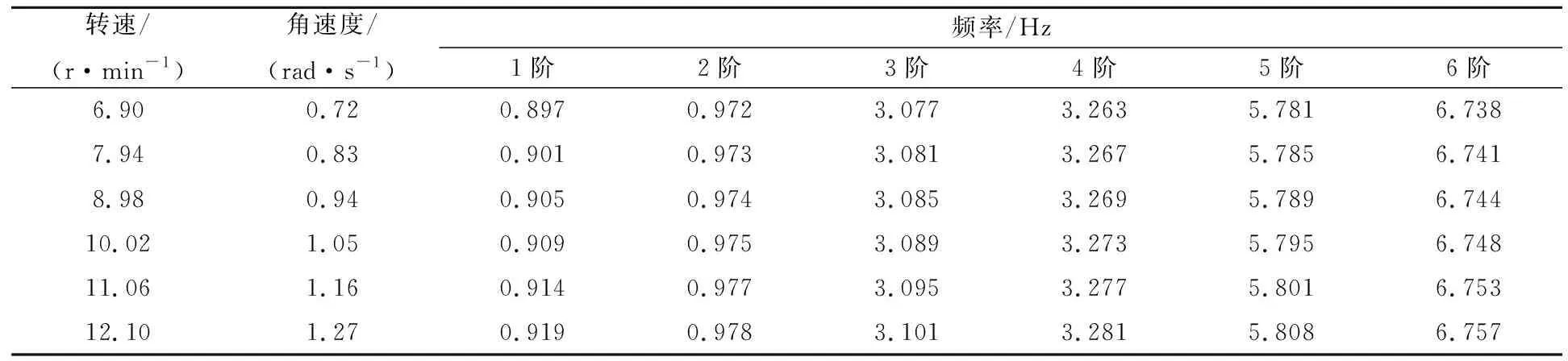
表4 不同转速下叶片前6阶频率

表4中,随叶片旋转速度增加,叶片固有频率增长呈现非线性,在转速较低时增长缓慢,转速高时固有频率增长较快,表明叶片应力刚化效应随叶片转速增加亦呈现非线性。随着叶片旋转速度增加,叶片第1阶频率由静止时0.887 Hz增大至旋转速度为12.1 r/min时的0.919 Hz,其频率增长3.6%;叶片第2阶频率由0.97 Hz增加至0.978 Hz,增幅为0.008 Hz,其频率增长0.83%;叶片第3阶频率由3.066 Hz增加至3.101 Hz,增幅为0.035 Hz,频率增长1.1%;中叶片第4阶频率由3.255 Hz增加至3.281 Hz,增加幅度为0.026 Hz,频率增长0.8%;叶片第5阶频率由5.768 Hz增加至5.808 Hz,增加幅度为0.04 Hz,频率增长0.7%;叶片第6阶频率由6.728 Hz增加至6.757 Hz,增加幅度为0.029 Hz,频率增长0.44%。

叶片在旋转过程中受离心力使得叶片固有频率提升,主要由于旋转过程中离心力产生应力刚化效应。叶片挥舞方向固有频率增长速度大于摆振方向叶片固有频率增长,表明叶片旋转运动和摆振运动之间耦合在一定程度减弱离心力对叶片固有频率影响,使得叶片摆振刚度降低,导致叶片摆振方向应力刚化效应减弱。

3.2 叶片振动坎贝尔图

根据坎贝尔图得到其振动转速、频率和振动幅值大小,对进一步研究叶片异常原因及设定极限振幅具有重要价值。首先坎贝尔先取叶片各转速点振动信号,作出振动自谱;然后以各谱线高度为半径,该谱线在频率轴的点为圆心作圆得到自谱图;最后将各振动信号自谱相结合,绘制各谐波斜线即为坎贝尔图。本研究中风轮切入转速为6.9 r/min,绘制叶片振动坎贝尔图如图7所示。

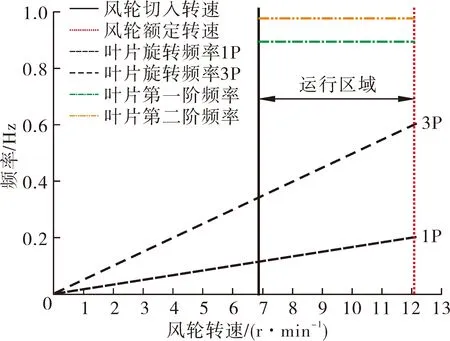
图7 叶片振动坎贝尔图

由图7可知,2条垂直线分别为风轮切入转速和额定转速,从原点出发射线表示叶片旋转频率,2条水平线为叶片振动第1阶、第2阶频率。风轮额定转速为12.1 r/min,得到叶片旋转频率1P为0.202 Hz,3P为0.606 Hz。根据前文可得,叶片第1阶固有频率为0.887 Hz,与叶片旋转频率1P、3P均相差77.5%和32.5%。叶片第1阶、第2阶固有频率与叶片旋转频率在风轮切入转速及额定转速区间不相交,即叶片在实际工作过程中不发生共振现象,符合叶片振动设计要求。

4 结论

1) 得到叶片前6阶振动频率和相对应模态振型,其中叶片第1阶固有频率为0.887 Hz,叶片在前6阶模态振型中未出现扭转振动,表明该叶片抗扭转能力较强。

2) 通过求解不同转速叶片固有频率,得到应力刚化效应对叶片第1阶固有频率影响最大,相对于静止时频率增长率达3.6%,对第6阶固有频率影响最小,增长率仅为0.44%。

3) 叶片振动坎贝尔图表明,叶片第1阶固有频率与其旋转频率1P和3P均相差分别为77.5%和32.5%,表明叶片在实际服役中不发生共振现象。