考虑轮胎移动载荷的沥青路面动力响应分析
王国盛 ,郭敏锐,吴启斌,石 鹏
(1.河南工学院 车辆与交通工程学院,河南 新乡 453003;2.黄淮学院 能源工程学院,河南 驻马店 463003;3.黄淮学院 智能制造学院,河南 驻马店463003)
0 引言
汽车在行驶过程中,通过轮胎作为传力媒介与路面接触,在路面产生相应的动力响应。根据我国现行的路面设计规范(JTGD50-2017),轮胎的接地压强为0.7MPa,路面的设计轴载为100kN,作用区域为双圆均布静态载荷,并采用多层弹性体为假设条件。尽管采用静态载荷可以解决很多工程问题,但是其没有考虑移动载荷导致的应力应变方向的改变,应力与应变响应的速度不同,以及轮胎的接地压强呈现不均匀分布并不断移动的特征;另外,路面还受到水平方向的移动载荷,包括沿轮胎行驶方向的纵向应力以及垂直于行驶方向的横向应力。因此,为了更加真实地反应路面受到的动力响应情况,考虑轮胎与路面接触应力的不均匀分布以及移动特征是十分必要的。
1 轮胎移动载荷作用形式
1.1 接触应力的不均匀分布特征
为满足不同路面行驶工况下附着力的需求,不同的轮胎胎面位置被加工出了不同的花纹。但是胎面花纹的不同使得路面与轮胎之间的相互作用出现不均匀分布的特征,随着轮胎的高速旋转,不同的轮胎与路面发生的动力响应也有了较大差别。参考国内外文献[1-2],选用某品牌275/80R22.5型号轮胎,轮胎胎面有4条纵向沟槽,将轮胎胎面处分为5条纵向凸起。如图1可看出轮胎模型及其胎面接地印记的形状。

图1 轮胎接地印记
纵向接地应力取值为竖向接地应力的0.16倍,横向接地应力取值为竖向接地应力的0.20倍[3-4],轮胎荷载的作用形式如表1所示。
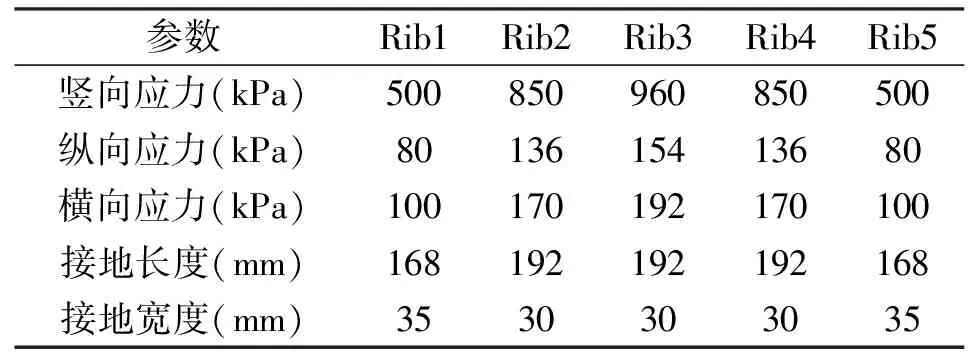
表1 单轴双轮接地应力参数表
1.2 轮胎移动载荷的施加
为了模拟单轴双轮车辆对路面施加移动载荷时的作用对象,在利用有限元软件Abaqus建立模型时,在轮胎前进方向上设置了两个载荷作用面。采用Fortran语言翻译器编写Utracload和Dload程序,以进行二次开发,其中Dload子程序用来施加竖向接触应力,Utracload用来施加纵向应力和横向应力,以实现轮胎载荷的向前移动[5]。
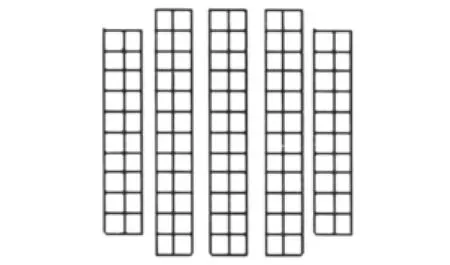
图2 路面载荷区网格模型
图2给出了路面载荷区网格模型,在轮胎与路面接触区域进行了网格细化,把轮胎的接地印记从左到右依次划分为Rib1、Rib2、Rib3、Rib4和Rib5 5个纵向凸起带,其中Rib2、Rib3、Rib4的接地长度相同,为192mm;Rib1和Rib5接地长度相同,为168mm;相邻两纵向凸起之间距离为10mm。假设轮胎行驶速度为45km/h,轮胎滚动半径489.17mm,轮胎0.24秒行驶完一个周期,移动距离3072mm。
2 路面三维有限元模型
2.1 有限元模型
利用Abaqus有限元软件建立路面结构模型,该模型为三维层状路面,长宽高分别为6000mm、6000mm和3760mm,其中X轴为道路的宽度方向(横向),Y轴为道路的深度方向(竖向),Z轴为轮胎前进的方向(纵向)。根据实际情况,在道路横向两侧、底面、纵向两侧分别限制X方向、Y方向、Z方向的位移,作为该模型的施加的边界条件[6-7]。对轮胎载荷作用区进行网格细化,选用软件中的C3D8R模型,该模型共有47656个单元,然后对网格分析检查,发现错误警告为0,如图3所示。

图3 路面三维有限元模型
2.2 路面结构和材料参数
为了研究轮胎移动载荷作用下路面的三向动力响应,须采用路面设计时实际采用的结构材料参数,如表2所示。
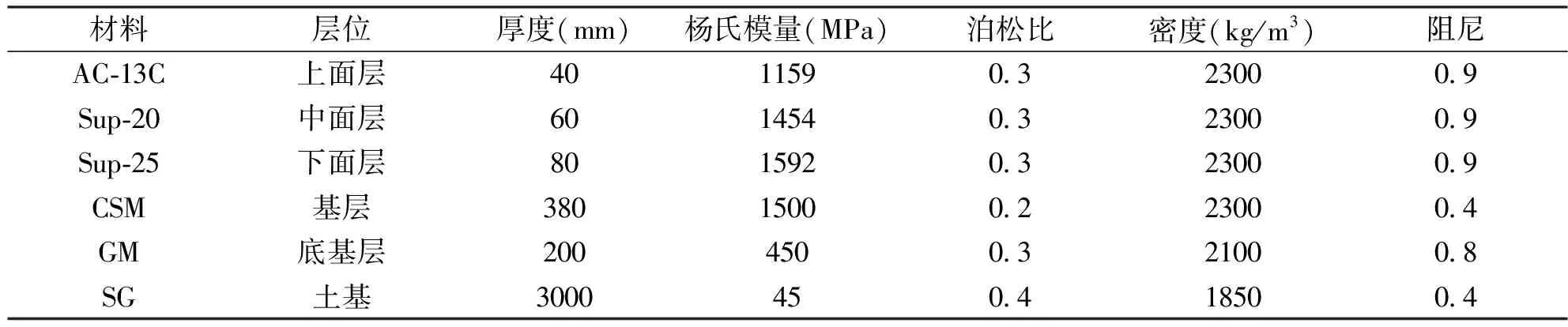
表2 路面结构材料参数
为表示沥青路面的动力响应与温度和时间的关系,本文采用剪切模量的Prony级数表示材料对时间的依赖性[8]。沥青路面材料模型Prony级数基本表达式如下列方程所示。级数的参数如表3和表4所示。
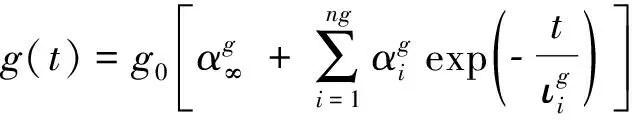
(1)
(2)
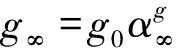
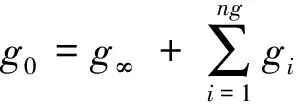
(3)
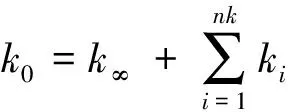
(4)
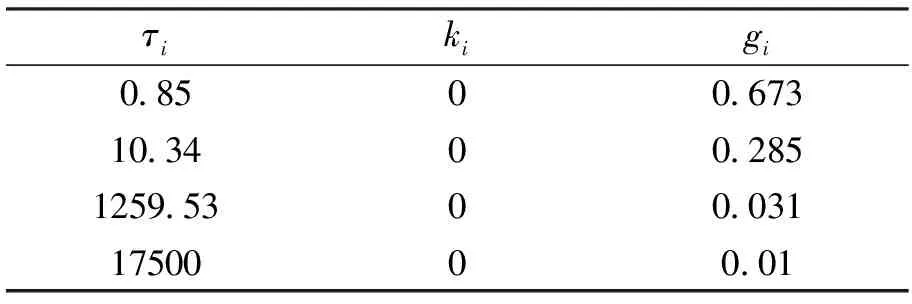
表3 上面层材料AC-13C的Prony级数参数
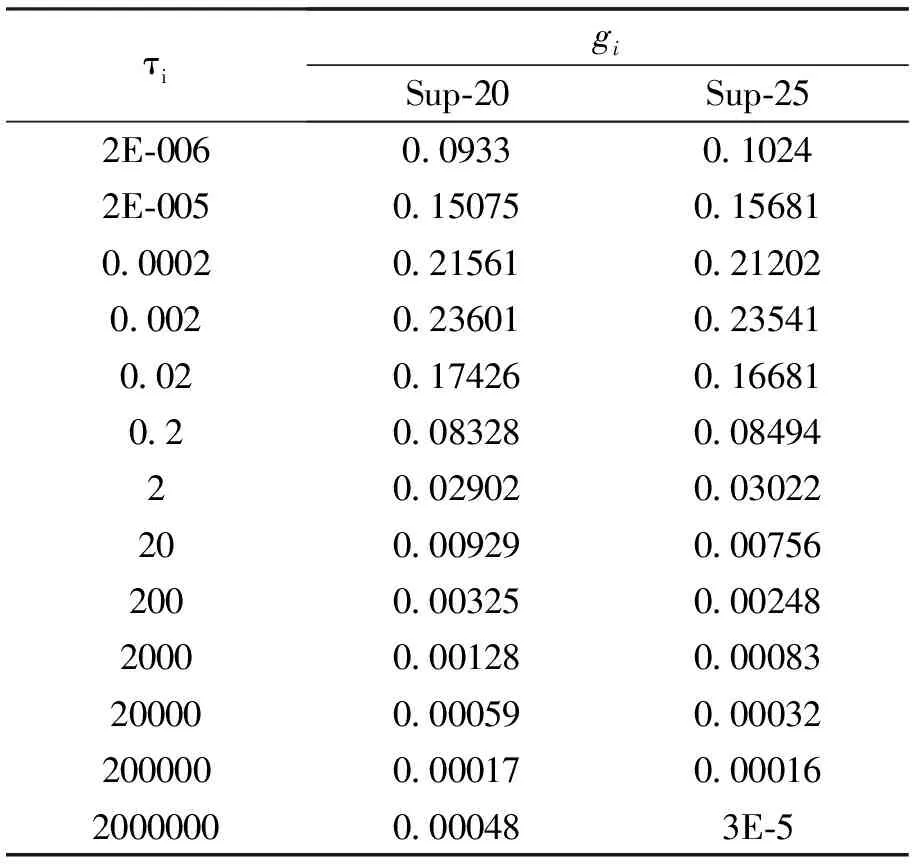
表4 中面层和下面层材料的Prony级数参数
通常采用松弛变量WLF方程来表示路面材料与温度的关系,其方程如下:
(5)
式中,αT为时温位移因子,Tref为参考温度,T为实际温度。
3 路面动力响应分析
选取合适的特征点作为研究分析对象,以获取路面各层在轮胎移动载荷作用下的动力响应[9]。由于有限元模型和轮胎载荷左右对称,这里选取右侧轮胎载荷中心线不同深度方向h=20mm、70mm、140mm、256mm处作为特征点,分别研究路面不同层位的竖向、横向、纵向的应力应变响应、剪应力和剪应变的响应规律[10]。
3.1 路面竖向应力应变响应
图4为特征点的竖向应力和应变时程变化曲线。可以看出在经过一个加载周期时间段内,随着路面深度的增加,路面的竖向应力逐渐减小,在上面层的竖向应力呈现最大值,而竖向应变的最大值却出现在中面层。在轮胎前进的0到0.09秒范围内,面层结构的竖向应变为较小的正值,表示刚开始是竖向拉应变,在外观上的表现为较小幅度的隆起。在0.09秒到0.14秒范围内,竖向应变为较大的负值,表示为竖向压应变。在0.14秒到0.24秒范围内,轮胎载荷驶离过后,竖向应变并没有马上回零,存在着一定程度的残余应变。可以看出在0.09秒到0.14秒范围内,轮胎加载下方的面层,基层上方出现竖向应力、竖向应变集中。
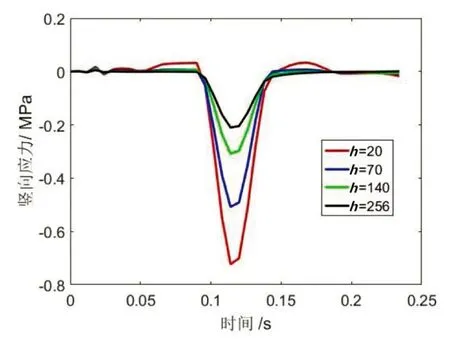
(a)竖向应力时程曲线
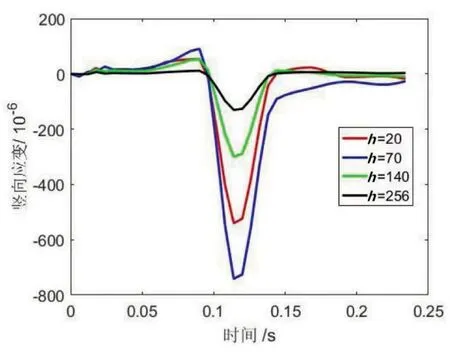
(b)竖向应变时程曲线图4 竖向应力应变时程曲线
3.2 路面横向应力应变响应
图5为特征点的横向应力和应变时程变化曲线。可以看出横向应力出现了和竖向应力类似的变化趋势,在轮胎作用范围的上、中、下三个面层均出现了横向应力集中现象,在中面层的横向应力最大,上面层的横向应力最大值小于下面层横向应力最大值。在基层上方的横向应力很小。横向应变的最大值同样出现在中面层,当中面层的横向应变达到最大值后再次衰减,在0.14秒到0.24秒范围内,横向应变也存在着残余应变,而且要大于纵向应变的残余应变。横向应变集中在上面层和中面层,表现为横向拉应变,导致轮胎胎冠接地处周围路面出现车辙等变形。比较图5(a)和图5(b),最大横向应力的最大值出现在0.11627秒,最大横向应变的最大值出现在0.14187秒,最大横向应变响应比最大横向应力响应晚0.0256秒。
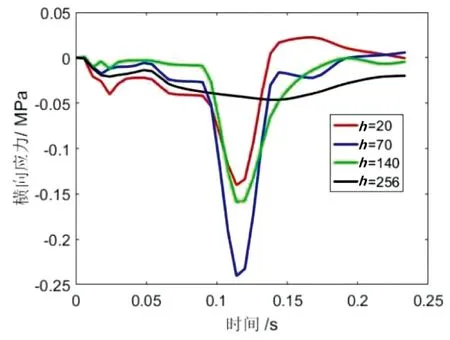
(a)横向应力时程曲线
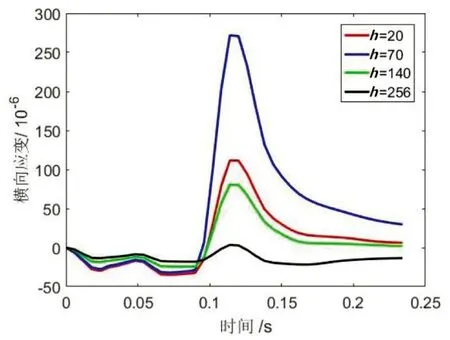
(b)横向应变时程曲线图5 横向应力应变时程曲线
3.3 路面纵向应力应变响应
图6为特征点的纵向应力和应变时程变化曲线。由图6(a)可知,在轮胎前进过程中,随着轮胎载荷的增加,上面层、中面层、下面层的纵向应力逐渐变大,达到最大值后逐渐减小。但在基层上方,由于接地印记范围内路面的黏弹性,纵向应力表现出了一定程度的波动。在0.09秒到0.15秒范围内,轮胎经过特征点正上方,纵向应力在中面层出现最大值。当轮胎驶离过后,在0.15秒到0.24秒范围内,存在一定的残余应力。由6(b)可知,在轮胎移动的整个周期内,纵向应变的正值和负值交替出现,表示纵向拉应变和纵向压应变在路面结构中交替出现。纵向拉伸应变的最大值出现在中面层,上面层和下面层的纵向应变值基本相同。这种在路面上反复出现的纵向拉伸和压缩应变容易导致疲劳损伤。如果路面反复碾压,则表明轮胎的载荷带出现从上到下的开裂。
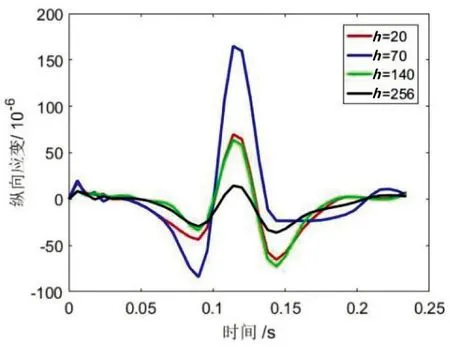
(b)纵向应变时程曲线图6 纵向应力应变时程曲线
3.4 剪应力和剪应变响应
图7为特征点的剪应力和剪应变时程变化曲线。在轮胎载荷经过前后,剪应力和剪应变都出现了正负值交变变化。剪应力正值和负值的绝对值比较接近,在路面的面层结构各层内部剪应力的大小基本相等,在基层上方剪应力要小于面层结构的剪应力。剪应变的最大值出现在下面层,剪应变集中在中面层和下面层,轮胎载荷作用时间也相应增大,在0.065秒到0.183秒范围内,正负剪应力和正负剪应变反复作用,这加剧了路面材料疲劳破坏和车辙破坏。
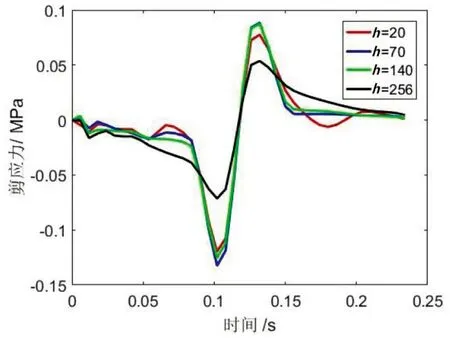
(a)剪应力时程曲线
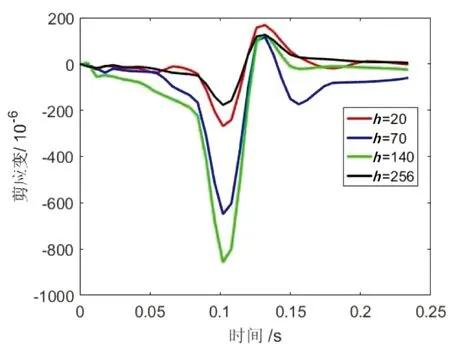
(b)剪应变时程曲线图7 剪应力和剪应变时程曲线
4 结论
(1)在轮胎移动载荷作用的整个周期内,路面载荷区竖向应力最大值出现在上面层,横纵向应力、剪应力的最大值出现在中面层。相同特征点处,竖向应力的幅值最大,纵向应力和横向应力幅值相当,剪应力幅值最小。
(2)在轮胎移动载荷作用的整个周期内,路面的竖向、横向、纵向应变最大值出现在中面层,剪应变最大值出现在中面层和下面层交界处。相同特征点处,横向应变幅值大于纵向应变幅值,竖向应变幅值大于横向应变幅值,剪应变的幅值略大于竖向应变幅值。纵向应变变化规律在不同的特征点处类似,拉-压应变的反复作用导致产生正剪应变和负剪应变交变变化,加剧了路面材料疲劳破坏和车辙破坏。因此,在路面设计过程中,不仅要考虑现有指标,而且要考虑应变指标。
(3)采用二次开发Abaqus软件的Dload和Utracload子程序,模拟轮胎实际移动载荷作用下的路面动力响应,结果出现正-负交变变化,应变响应略微慢于应力响应。这是传统静力分析无法做到的,所以路面动力响应应该考虑轮胎移动载荷的作用。

