方钢管灌浆连接节点轴压性能试验研究

李 涛，肖 彬，李 勇，李 炀，王小平2，，邵永波

(1.武汉理工大学 土木工程与建筑学院，湖北 武汉 430000；2.武汉理工大学 海南研究院，海南 三亚 572000；3.西南石油大学 土木工程与测绘学院，四川 成都 610000)

目前，我国建筑行业的生产效率低、模块化程度低、现场劳动力需求大，工业化和城镇化的快速发展造成了大量的建筑能源消耗[1].面对当前困局，我国建筑行业必须顺应时代发展进行转型升级，大力推行模块化建筑.模块化建筑拥有高建造效率、低污染、可持续发展等优点，不同于传统建筑施工方式，模块装配式建筑的建造方式为：首先将结构划分为单个房间单元模块，随后在工厂完成每个单元模块的结构建造、室内装饰和水电安装等，再将预制完成的单元模块运输至现场并使用起重机进行吊装，最后连接成结构整体.模块化建筑按主要建筑材料可分为钢结构模块、预制混凝土模块和木结构模块.其中钢结构模块近年来在我国应用越来越多，例如火神山和雷神山等方舱医院均由钢结构模块搭建而成[2]，因此研究和推广钢结构模块建筑是非常有必要的.

钢结构模块之间的连接方式是该类建筑的关键.国内外学者提出许多钢结构模块之间的连接方式[3-5]，并进行了相关研究.卢林枫等[6]提出梯形侧板加强式节点，其梁柱连接形式为栓焊混合连接，对此节点进行了循环荷载作用下的变参分析.研究结果表明：梯形侧板加强式节点均在距蒙皮板约2/3梁高处梁全截面发生明显的屈曲变形，形成明显的塑性铰并有效外移.王玉田等[7]采用了对梁柱连接局部加强和转移塑性铰位置的几种连接形式，进行了低周反复荷载试验，研究结果表明：加强型梁柱连接虽然在地震荷载作用下对承载力的提高并不明显，但可以保证有效地将塑性铰外移，提高节点的延性.Chen等[8-9]提出悬臂梁段扩翼加强型梁柱节点，设计了7个足尺模型，对其进行了有限元模拟及低周循环试验.研究结果表明：无论是采用全焊连接还是栓焊混合连接的翼缘加强型试件，都在远离柱面的梁截面上形成塑性铰，并具有良好的延性.郁有升等[9]提出一种新型梁柱刚性节点，在悬臂梁与框架梁的上、下翼缘交互处放置拼接板，并通过螺栓将其连接，对该新型节点进行了有限元分析.研究结果表明：试件的延性和耗能能力较好，螺栓数量、盖板宽度及厚度、悬臂梁段长度对节点的承载力和延性均有一定影响.张爱林等[11]提出了一种端板型装配式钢结构梁柱节点，对该节点进行了数值模拟，分析了关键参数对节点力学性能的影响规律，研究结果表明：通过合理设计螺栓及翼缘连接盖板相关参数可保证节点承载能力，确保梁柱等主要构件不发生破坏，实现节点的震后快速修复.Chen等[12-13]提出了柱内套管-梁螺栓连接钢模块装配式连接节点(图1所示)，并对其静力性能和抗震性能进行了试验和有限元研究.研究结果表明：上下柱之间的间隙会影响节点的变形模式和载荷分布，焊缝质量是确保结构整体安全的关键.刘学春等[14]提出一种新型模块化装配式建筑体系，该体系中的上下模块柱采用法兰盘连接，对节点进行了有限元分析，研究结果表明：螺栓规格较大的模型承载力更高，而法兰盘厚度对模型承载力的影响不大.上述连接方式需要考虑螺栓孔距和板件厚度，需要的螺栓数量大，安装精度要求高，施工较为困难.在海洋结构桩基与水下基础承插式灌浆连接中，一般在连接段设置抗剪键，其可以有效的提高连接段的受力性能[15-17].海洋结构一般使用圆钢管，而模块装配式钢结构中一般使用的为方钢管，因此有必要开展方钢管灌浆节点的力学性能研究.目前对方钢管灌浆节点的研究较少，文献检索发现Dai等[18]研究了方钢管灌浆套管节点轴压性能，对比了钢纤维灌浆料与普通灌浆料对试件极限承载能力的影响，分析了灌浆料失效模式.研究结果表明：受压隔离体斜面角度与灌浆料厚度和抗剪键间距存在函数关系，隔离体的数量及其斜面角度决定节点的极限承载能力.Huang等[19]进行了新型超高性能纤维钢筋混凝土灌浆连接的轴向试验、数值模拟和理论分析，在试验和有限元的基础上提出了一种可预测轴向荷载的理论模型.研究结果表明：试件出现了内管断裂和灌浆剪切破碎两种破坏模式.He等[20]开展了10个试件的轴向荷载试验，分析了不同参数对试件极限承载能力的影响.研究结果表明：试件的极限承载能力随着灌浆段长度的增加而增加，当灌浆段长度足够时，极限承载能力可达到外管截面的承载力.抗剪键的尺寸和间距、内外套筒之间的间隙和外套筒的厚度分别对极限承载能力有着不同的影响.

图1 Chen等[12] 提出的钢模块连接节点

本文借鉴海洋结构中的桩基与水下基础灌浆连接，拟提出图2所示的灌浆连接梁柱节点，即在上下方钢管柱内壁和内部套筒外壁设置抗剪键，并通过灌浆连接.由于目前尚缺乏方钢管灌浆连接及其抗剪键设计方法，因此本文中设计了7个灌浆方钢管连接轴心受压试件，用于研究抗剪键数量、抗剪键尺寸和间距等对方钢管灌浆连接的极限承载力的影响规律，研究结果将在下一步中用于指导图2所示的模块装配式钢结构灌浆梁柱连接节点设计.

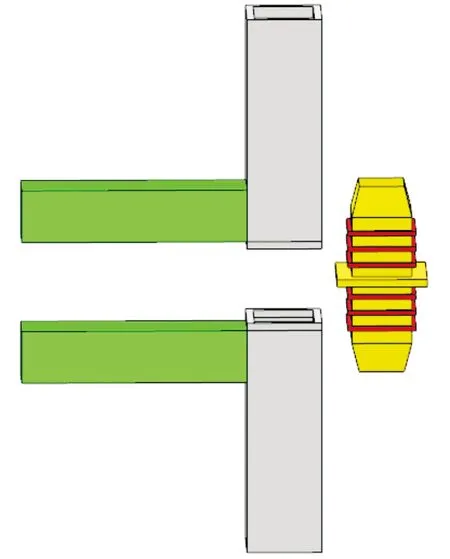
图2 灌浆连接梁柱节点

1 轴心受压试验概况

1.1 试件尺寸设计

本试验共设计7个灌浆连接轴心受压试件，试件构造如图3所示.外套筒内壁设有抗剪键，内套筒外壁设有抗剪键，在内外套筒间隙之间灌注高强灌浆料，并于底部设置横隔板防止灌浆料的流失.内外套筒均采用方形钢管，外套筒的截面尺寸为150 mm×150 mm×8 mm，内套筒钢管截面尺寸为100 mm×100 mm×8 mm，灌浆方钢管或圆钢管剖面如图4所示.对于方钢管，其中Ds为方钢管外套筒外边长，Dg为方钢管外套筒内边长，Dp为方钢管内套筒外边长；对于圆钢管，其中Ds为圆钢管外套筒外径，Dg为圆钢管外套筒内径，Dp为圆钢管内套筒外径.tg为内外套筒之间的空腔壁厚，h为抗剪键高度，w为抗剪键厚度，s为抗剪键间距，L1为灌浆长度，L2为试件总高度，钢材强度等级为Q235B.

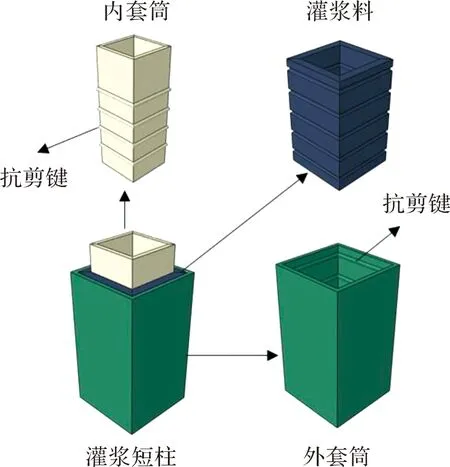
图3 试件构造图

图4 方钢管或圆钢管灌浆节点剖面图

本试验制作的为方钢管灌浆连接节点，没有相关的规范可用于抗剪键参数设计，因此参考了API-RP-2A-WSD(2014)[21]中圆形钢管灌浆连接的抗剪键参数设计方法.该规范规定圆形钢管灌浆连接设计关键几何参数需满足以下要求.

(1)

(2)

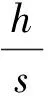
(3)

(4)

按照等效周长原则，将方钢管等效成圆形钢管.等效外套筒内径Dg为171 mm，内套筒外径Dp为127 mm，代入以上公式可知关键参数的取值范围应满足以下关系式：

3.8≤tg≤24.4

(5)

15.9≤s≤50.8

(6)

1.6≤h≤5.1

(7)

9≤w≤15.3

(8)

因加工条件的限值，难以制作高度h小于5.1 mm的抗剪键，本次试验制作的抗剪键高度均放大至6.5 mm，h/s值略微超出公式(1)～(3)的范围.抗剪键宽度w取10 mm，间距s有两组数据，分别为45和55 mm，其中55 mm略微超出公式(1)～(6)的范围.试件详细尺寸见表1.

表1 试件几何尺寸

1.2 材性试验

在正式加载试验之前依照《金属材料室温拉伸试验方法》(GB/T228.1—2021)[22]对钢材进行了材性试验，由于方钢管角部存在材料硬化现象会导致方钢管角部和中部的材料强度产生差异，因此本次钢材拉伸试验的试件分别从内套筒中部、内套筒角部、外套筒中部、外套筒角部选取，共进行4组材性试验，每组取3个试件.

本试验在武汉理工大学材料研究与测试中心力学试验室完成，其中拉伸试件的引伸标距为50 mm，4组试件的平均屈服强度、抗拉强度、伸长率、见表2.

表2 钢材材性

本试验采用CGM-85钢筋连接用套筒灌浆料，根据 GB/T 17671《水泥胶砂强度检验方法》[23]，浇筑6个灌浆料标准试块(40 mm×40 mm×160 mm)，并与灌浆连接试件同时存放于室内自然养护至28天.本次试验在武汉理工大学土木工程试验室的30 t微机控制电液伺服万能试验机上进行.根据规范相关要求最终测得灌浆料平均抗压强度为52.69 MPa.

1.3 试验测试及应变片花布置

试验在武汉理工大学土木工程试验室中300 t液压加载机上进行，加载装置见图5.试件上方放置力传感器，用于记录试验过程的轴向荷载，试验机加载端设置位移传感器，用于记录试验过程中的竖向位移.应变数据采集装置使用DH3816N静态应力应变测试分析系统.为了研究力在套筒-灌浆料界面上的传递情况，以及套筒对灌浆料的约束作用，每个试件的外套筒侧壁布置3个应变花(应变2、5、8不记录)，分别位于外套筒上部、中部和底部抗剪键的位置(如图6所示).试验加载方式为位移控制，加载速率为1 mm/min，数据采集频率为1 Hz，试验结束的标志为荷载-位移曲线出现明显下降段，荷载值下降到峰值的60%或者试件完全破坏.

图5 灌浆节点加载装置

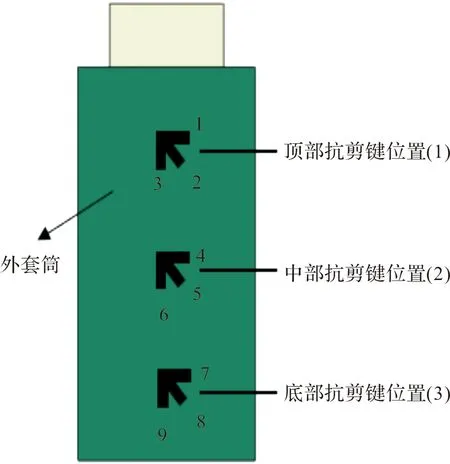
图6 应变花布置

2 试验现象与结果分析

2.1 试验现象

图7所示为测试的试件停止加载时的表面破坏现象，由于试验操作失误，未能顺利完成试件S6加载，因此本文没有给出试件S6的相关试验结果.试件S1内部未设置抗剪键，加载前期处于弹性阶段，试件未有明显变化，当内套筒位移达到1 mm左右时，可听见试件传出吱吱声，可能因为内套筒外壁与粘附在其表面的灌浆料开始剥离，但外套筒无变化，达到峰值荷载后内套筒位移继续增大，承载力开始下降，下降至极限承载力的60%左右时试验终止，此时内套筒相对外套筒向下位移约8 mm，试件表面破坏形态如图7(a)所示.

图7 试件表面破坏现象

试件S2-S5内部设置有不同数量和间距的抗剪键，其表面破坏现象仅呈现出不同的内套筒贯入位移和不同程度上的外套筒鼓曲变形.以试件S2为例，位移达到1.3 mm左右时，试件开始传出吱吱声，同时肉眼观察到外套筒侧壁轻微隆起，位移达到6 mm左右时，达到峰值荷载，随后承载力开始下降，破坏形式为内套筒压入外套筒，灌浆料压碎，试件表面破坏形态如图7(b)所示.其余试件的表面破坏形态(S3-S5)分别如图7(c)-图7(e)所示.

试件S7加载初期试件处于弹性阶段，位移达到2.5 mm左右时，外套筒端部开始发生鼓曲变形，试件传出吱吱声，承载力继续增加，当位移达到3 mm左右时，外套筒下部鼓曲变形进一步增大，同时变形面继续向下延伸，此时达到试件极限承载力，承载力下降至极限荷载的60%左右时结束试验，试件表面破坏形态如图7(f)所示.

2.2 破坏模式分析

根据文献[24]和文献[25]报道，圆钢管灌浆连接中的灌浆料存在2种主要的破坏模式(如图8所示)，分别为灌浆料的局压破坏和剪切破坏.当抗剪键的高度h与抗剪键间的距离s的比值处于合适的范围内时，灌浆料会发生局压破坏，表现为抗剪键之间的灌浆料被压碎.局压破坏可分为两种：当抗剪键间的距离s适当时，裂缝出现在内外套筒的相邻抗剪键之间，夹缝灌浆料被压碎形成受压隔离体，如图8(a)中的Case A；当抗剪键间的距离s偏小时，裂缝沿着内套筒的抗剪键向外套筒上下相邻抗剪键之间发展，如图8(a)中的Case B.当抗剪键高度h过大时，会发生灌浆料剪切破坏，如图8(b)所示，表现为灌浆料在抗剪键顶部的平面上出现裂缝，剪切面两边发生相对滑移.其中灌浆料发生局压破坏为期望的破坏模式.

图8 灌浆料的可能的破坏模式

为进一步地研究灌浆料的破坏模式，将本次试验的6个试件切开.除试件S1和S7以外，其余试件(S2～S5)均发生灌浆料局压破坏中的Case A，如图9(a)所示.可以观察到裂缝沿内套筒上的抗剪键向着相邻下方外套筒上的抗剪键传递，上下两条连贯的斜向裂缝进一步地使灌浆料形成受压隔离体.文献[26]指出，应力扩散产生的横向应力和荷载竖向传递的纵向应力共同作用在灌浆料内部产生劈裂力，劈裂力沿内外抗剪键将灌浆料劈开形成斜向裂缝.受压隔离体是试件承受轴向荷载和弯矩重要组成主要部分[27]，同时隔离体的数量、裂缝形成的角度及长度均不同程度上影响着试件的滑移承载力和极限承载力.

图9 试件S2和S7剖切面

试件S1中未设置抗剪键，所以不会发生局压破坏.试件S7的剖切截面如图9(b)所示，可以发现夹层灌浆料未发生破坏，未出现图8中的破坏模式，进一步地验证了试件S7是由于外套筒端部屈曲而破坏.结合图10可知，试件S4和S7的极限承载能力均超过了外套筒的截面屈服承载能力(此处屈服强度偏保守的选取外套管中部区域强度)，而Dai等[18]所研究的方钢管灌浆连接节点的轴压承载力仅可以达到钢管截面承载力的39%～53%.

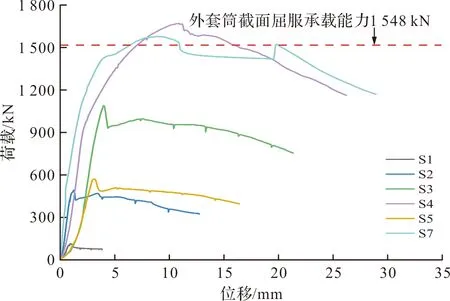
图10 荷载位移曲线汇总

2.3 荷载位移曲线分析

由图10可知所有试件在整个加载过程都经历了弹性阶段、弹塑性阶段和承载能力下降阶段，荷载位移曲线的走势相似.加载初期，试件的承载力与控制位移大致成线性关系，试件处于弹性阶段，此时荷载增长速度较快.随着控制位移的增大，荷载增长速度放缓，试件处于弹塑性阶段.当试件达到极限承载力后，因外套筒鼓曲或者灌浆料被剪压破碎导致承载力下降.其中试件S1峰值荷载和极限位移分别只有113.85 kN和4 mm，且在达到峰值荷载以后曲线出现相对较长的平滑段，其原因是试件S1中没有设置抗剪键，整个试件的承载能力完全由灌浆料与内套筒之间的摩擦力提供，试件达到峰值荷载以后，灌浆料与内套筒表面开始出现相对滑移导致承载能力降低.各个试件的极限承载能力见表3.

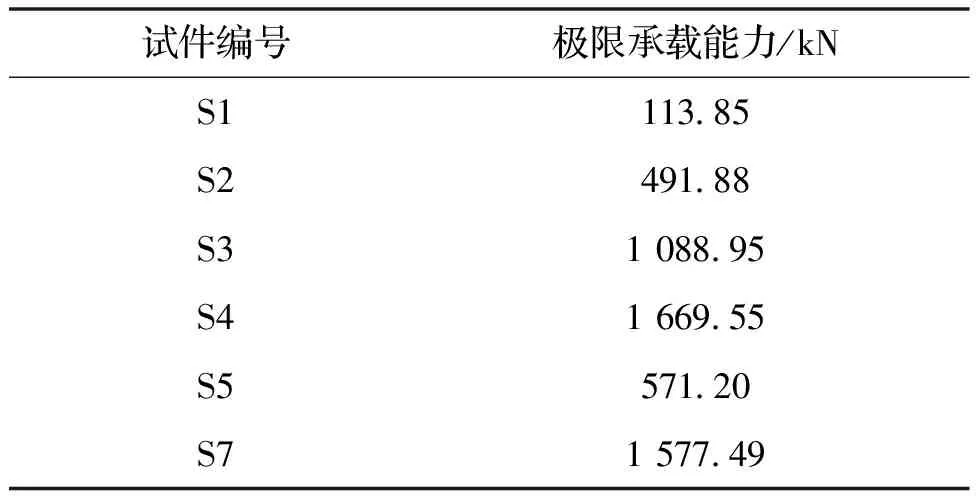
表3 极限承载能力

2.4 应变分析

通过外套筒应变分析可以了解到试件在轴压破坏过程中钢管与灌浆料的相互作用情况，外套筒最上方的抗剪键为位置1，依次往下.将各试件极限荷载下各测点的应变提取并绘制于图11，各试件的荷载应变曲线如图12所示.应变值为正，表明该方向受拉，应变值为负，表明该方向受压.在纵向应变上，不同高度上的应变变化体现了荷载的传递机制.由图11和图12可以发现，外套筒轴向均受压，而环向均受拉.抗剪键数量大于2的试件(S3、S4、S7)中，纵向应变从顶部抗剪键至底部抗剪键依次增加，表明轴向荷载沿着外套筒壁逐级向下传递，抗剪键数量等于2的试件(S2、S5)各测点纵向应变基本相同.对于环向应变上，所有的试件均表现出了沿着外套筒壁从上至下应变逐渐增加的趋势，这表明外套筒对于夹层灌浆料的围压沿着灌浆料顶部至底部逐渐增强，但是并非所有试件所有点位的环向应变达到了外套筒屈服应变.

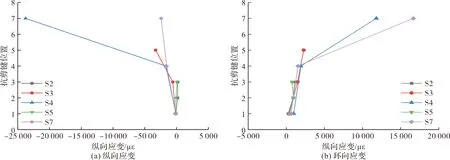
图11 外套筒应变发展情况

图12 荷载-应变曲线

3 不同参数对承载能力的影响

3.1 抗剪键数量对承载力的影响

将6个试件分为3组，第一组抗剪键数量分别为0和2，抗剪键间距为45 mm.第二组抗剪键数量分别为2，4，6，抗剪键间距为45 mm.第三组抗剪键数量分别为2和6，抗剪键间距为55 mm.其中，受压隔离体数量等于抗剪键数量减去1，三组试件的极限承载能力对比如图13所示.第一组中S2(492 kN)相较于S1(114 kN)增加了332%.由此可见，增加抗剪键的数量可以显著提升灌浆连接的极限承载能力，结合图10可知设置抗剪键以后可以显著增加试件的峰值荷载位移.

图13 抗剪键数量对极限承载力的影响

第二组中S3(1 089 kN)相较于S2(492 kN)和S4(1 670 kN)相较于S2(492 kN)分别增加了121%和239%.3个试件在极限承载能力上呈现出规律性差异，每增加1个受压隔离体，承载力增加约300 kN左右.第三组中S7(1 577 kN)相较于S5(571 kN)增加了176%.每增加1个受压隔离体，承载能力增加约250 kN左右.结合第二组数据可知，随着h/s变小，单个受压隔离体提升承载能力的效率会降低.

3.2 抗剪键间距对承载力的影响

将其中4个试件分为两组，第一组抗剪键数量为2，抗剪键间距为45 mm，第二组抗剪键数量为6，抗剪键间距为55 mm，其极限承载能力对比见图14.第一组中S5(571 kN)相较于S2(492 kN)提高了约16%，其原因可能来源于抗剪键间距增加后抗剪键间受压隔离体长度的增加.试件S7(1 577 kN)相较于试件S4(1 670 kN)承载能力略低，结合图10可知在位移10～20 mm过程中试件S7的承载能力出现了一小段的下降，其原因在于试件S7的外套筒端部达到了其截面承载能力，导致试件极限承载力只能达到1 577 kN.可见在长度较大的试件中，灌浆料承载能力提高的同时，外套筒钢管的钢材强度也需要进行相应的匹配.

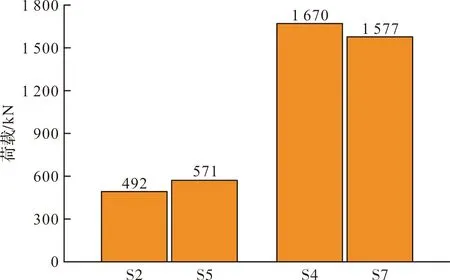
图14 抗剪键间距对极限承载力的影响

4 结论

为了研究灌浆连接方式的力学性能，本文设计了7个方钢管灌浆连接轴心受压试件，研究了抗剪键数量、抗剪键间距对极限承载力的影响，分析了轴向荷载在外套筒上的传递机制和试件的破坏模式.得到如下结论：

(1)合理的设计方钢管灌浆连接节点能够使连接段的轴压承载力达到连接钢管的截面承载力，从而使灌浆连接节点在轴压作用下破坏发生在钢管上.h/s在合适的范围内，试件会发生预期的局压破坏；

(2)增加受压隔离体的数量可以显著提升试件的极限承载能力，但随着h/s变小，单个受压隔离体提升极限承载能力的效率会降低.抗剪键数量一定的情况下，适当的增加抗剪键间距s能够提升灌浆节点的轴压承载能力；

(3)随着灌浆段长度的增加，试件峰值承载力增加的同时，对应的轴压位移也同时增大；三个测点的纵向应变的差异变大，表明纵向荷载的传递存在滞后效应；环向应变从上至下依次增加，表明外套筒对灌浆料的约束效应逐渐增强.