高强不锈钢筋与UHPC的粘结锚固性能研究

李海云，吴文辉，侯 楠，李 然，邓瑞婷，赵 晶

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043；2.旭阳工程有限公司邢台分公司，河北 邢台 054000；3.广州地铁设计研究院股份有限公司，广东 广州 510000)

钢筋混凝土构件抗力计算的前提是二者之间无相对滑移，这就需要钢筋与混凝土之间有充足的粘结力，而钢筋锈蚀是影响二者之间粘结力的重要因素.在一般情况下钢筋混凝土构件都是以带裂状态工作，空气中的二氧化碳会破坏钢筋表面的钝化膜[1]，加速钢筋锈蚀降低钢筋与混凝土之间的粘结力，影响钢筋混凝土结构的耐久性[2].超高性能混凝土(ultra-high performance concrete，UHPC)具有超高的强度和良好的塑性性能[3]，将普通混凝土用UHPC代替，可以有效的解决混凝土开裂的问题.不锈钢筋具有优良的耐腐蚀性能，将普通钢筋用不锈钢筋代替，可从根本上解决钢筋的锈蚀问题[4]，提高构件的耐久性.早期就有学者对二者之间的粘结性能进行试验研究[5]，并在试验研究的基础上建立粘结滑移本构模型[6-7].目前.国内外对粘结性能的研究主要从钢筋种类[8-12]、混凝土等级[13-16]、钢筋锈蚀率[17-18]等影响因素对粘结强度的影响，和建立钢筋混凝土的粘结滑移本构关系[19-23].随着科技发展，新的科研手段不断涌现，也有部分学者尝试利用有限元的方法研究钢筋与混凝土之间的粘结滑移本构关系[24-25].

本次试验设计了12组共36件不锈钢筋与超高性能混凝土的拉拔试样，研究钢筋种类、钢筋直径、相对保护层厚度、相对锚固长度、配箍率等参数对不锈钢筋和超高性能混凝土粘结性能的影响.

1 拉拔试验

1.1 材料性能试验

根据《混凝土物理力学性能试验方法标准》(GB/T50081—2019)[26]制作了6个边长100 mm ×100 mm×100 mm的立方体超高性能混凝土试块，采用微机屏显式液压压力试验机，以0.6 MPa/s的速率对标准试块进行加载，测得混凝土的立方体抗压强度(取测试值的平均值)fcu为120 MPa.

本次试验采用三种带肋钢筋和一种光圆钢筋(如图1所示)，三种带肋钢筋的横肋间距都为10 mm，BS-R不锈钢筋的横肋与普通钢筋大致相同，纵肋略高于普通钢筋；AS-R不锈钢筋的横肋不是标准的月牙形状，而是中间与两端等宽的矩形横肋，其宽度略宽于普通钢筋与DS-R不锈钢筋，但高度略低于两者，纵肋尺寸与HRB-600-S大致相同.

图1 试验所选用钢筋

根据《金属材料试验拉伸》[27](GB/T 228.1-2015)对钢筋进行取样，每种钢筋取2个试样，采用SHT4106-G微机控制电液伺服万能试验机，以10 MPa/s的速率对钢筋试样进行拉伸，得到钢筋的极限抗拉强度，并以残余应变的0.2%所对应的荷载作为不锈钢的屈服强度，其力学性能见表1，不锈钢分为双相体不锈钢和奥氏体不锈钢，除普通钢筋外钢筋编号中D代表双相体不锈钢，A代表奥氏体不锈钢，R代表带肋钢筋，P代表光圆钢筋，d为钢筋直径，fy为钢筋屈服强度，fu为钢筋极限强度.

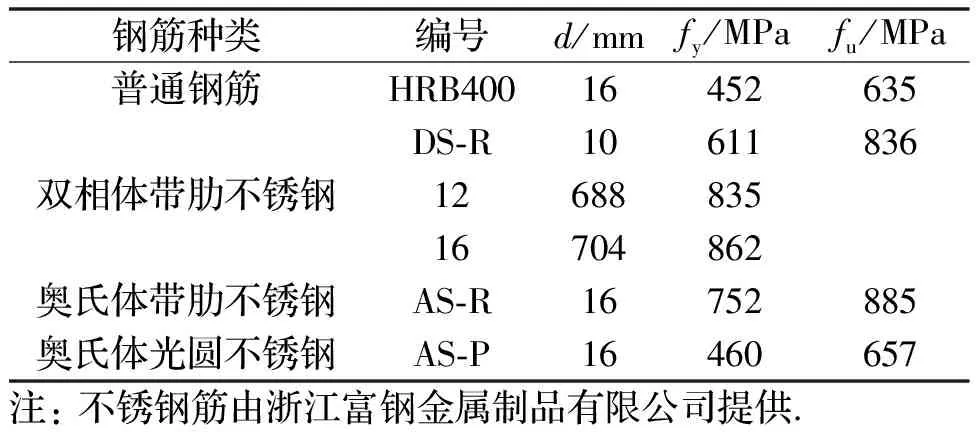
表1 钢筋的物理力学性能

1.2 试样设计

拉拔试验试样分为5个控制变量(钢筋类型、钢筋直径、相对保护层厚度、相对锚固长度和配箍率)对照组，试样加工示意如图2所示(以HC-HSS-2为例)，为了测试粘结应力的分布，将钢筋沿轴线切割成两瓣，在每瓣的中心进行铣槽(如图3)，凹槽贯穿整个钢筋，在凹槽内贴应变片并引出导线，用环氧树脂将两瓣钢筋进行粘合使其恢复原貌(如图4所示).每个试样配置三个相同的试块，以免发生偶然情况造成数据异常，各试样参数如表2所示.

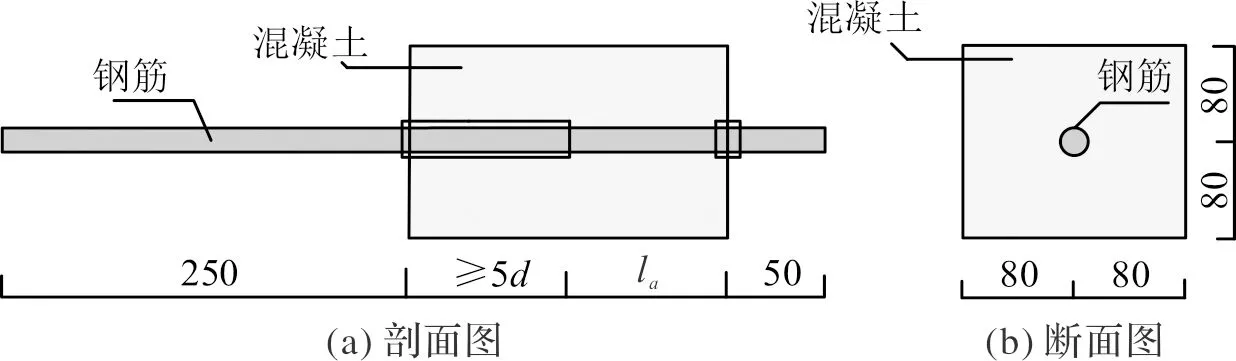
图2 拉拔试件(mm)

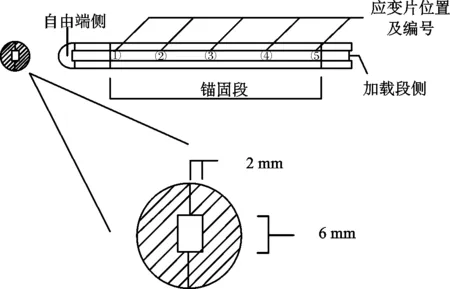
图3 钢筋加工示意图以及应变片位置(mm)

图4 钢筋加工与粘合后实物图

为了避免反力板对试样内部的锚固段造成伤害，将直径略大于钢筋的PVC管套在试样的加载端，并将其密封防止PVC管灌浆导致锚固长度增加.浇筑并振捣之后养护28 d后开始拉拔试验.

1.3 加载方案

根据《混凝土物理力学性能试验方法标准》(GB/T50081—2019)，拉拔试验采用SHT4106-G微机控制电液伺服万能试验机，为方便试样在试验机上的安装，制作了放置试样的辅助反力架，在反力架内设置位移计测量试件钢筋的自由端滑移，辅助反力架和安装在试验机上的试样分别如图5所示.试验时固定反力架的上加载螺栓，以0.3 kN/s的速率对试件钢筋进行加载，试验荷载通过计算机采集.

图5 试验装置示意图

2 试验现象及结果

2.1 破坏形态

表3给出了本次拉拔试验各试样的破坏形式，可以看出，试样的主要破坏形式为钢筋拔出破坏，有少量试件破坏形式为钢筋拉断或混凝土劈裂破坏.

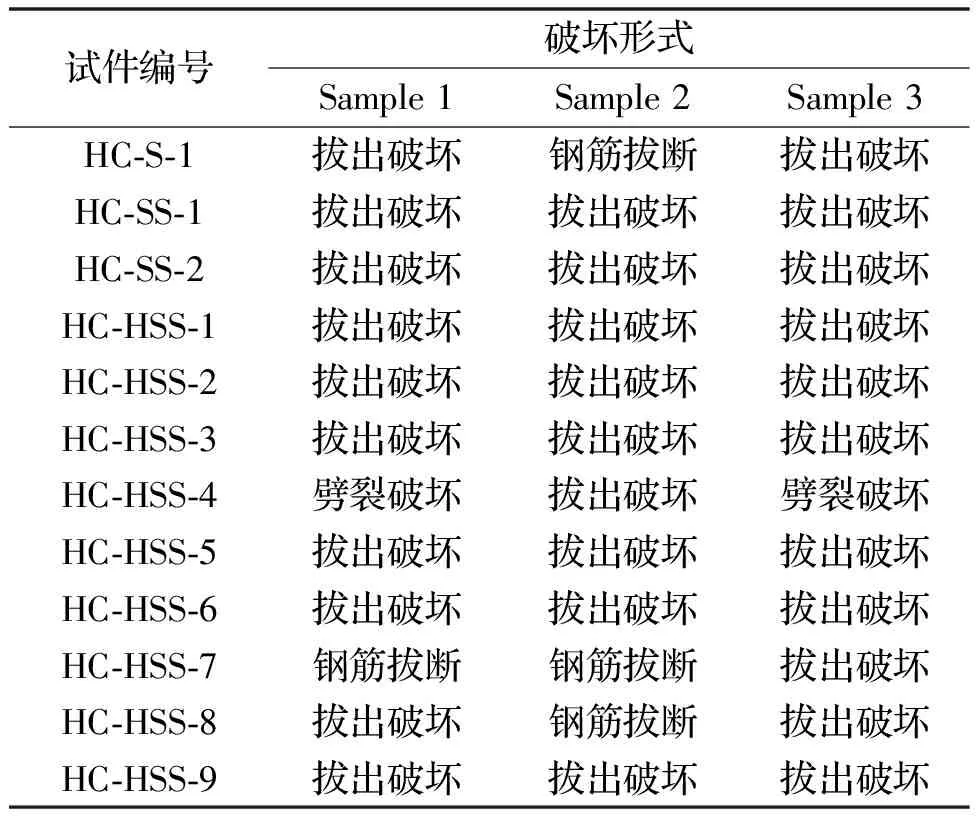
表3 中心拉拔试验破坏形式

本次试验以钢筋拔出破坏为主，存在少量混凝土劈裂破坏和钢筋拔断破坏.对于混凝土劈裂破坏，当荷载加载至约峰值荷载的80%时，试样混凝土开始出现裂缝，同时混凝土土体内部发出钢纤维拉扯产生的声响，随着荷载增大，裂缝逐渐扩展至贯穿混凝土体，此时荷载达到峰值，该过程较为缓慢，试样被劈裂为2瓣或3瓣，试样的侧面出现贯通的裂缝，图6为其中的典型破坏图片；而钢筋拔出破坏，试验过程中随着荷载的增加，开始时试样无变化，当荷载达到峰值荷载时，钢筋和少量混凝土慢慢被拔出(如图7)，随后荷载逐渐下降，该下降过程同样较为缓慢；钢筋拔断破坏是钢筋与混凝土之间的锚固力超过了钢筋自身的强度，其荷载位移曲线类似于钢材拉伸试验的应力-应变曲线(如图8)，破坏时比较突然.

图6 劈裂破坏试件

图7 拔出破坏试件

图8 HC-S-1试验曲线

2.2 试验结果

试样的粘结强度计算公式如式(1)所示.

其中，τ为平均粘结应力，MPa；Fu为极限拉拔力，kN，其余字母含义同前.

(1)

分析试验结果可得每组数据的变异系数范围介于0.04与0.21之间，差别较小，故取每组3个试样的平均值作为其粘结强度.各试样相关数据如表4.不同影响因素下试样的粘结-滑移曲线如图9所示.

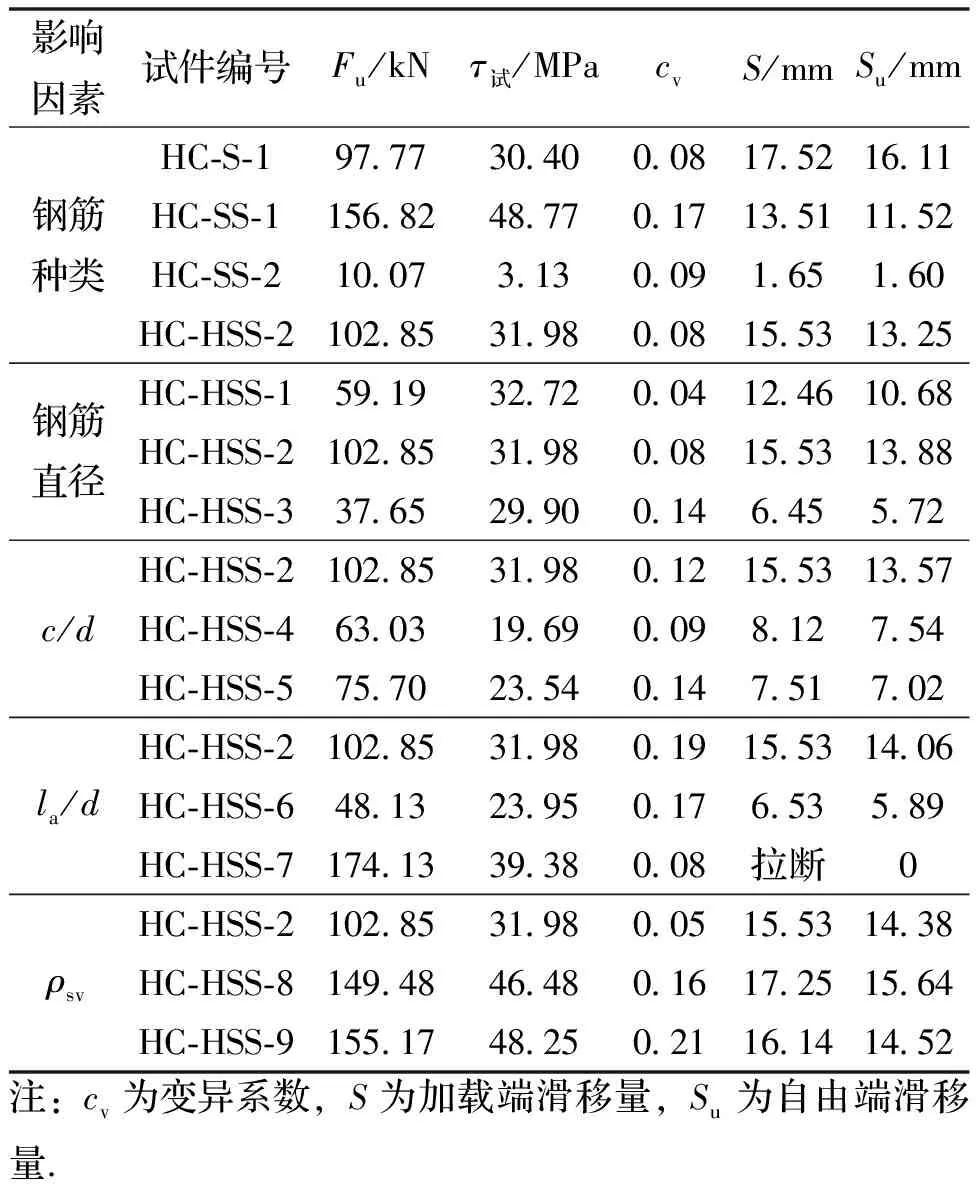
表4 试样极限拉拔力及粘结强度试验值

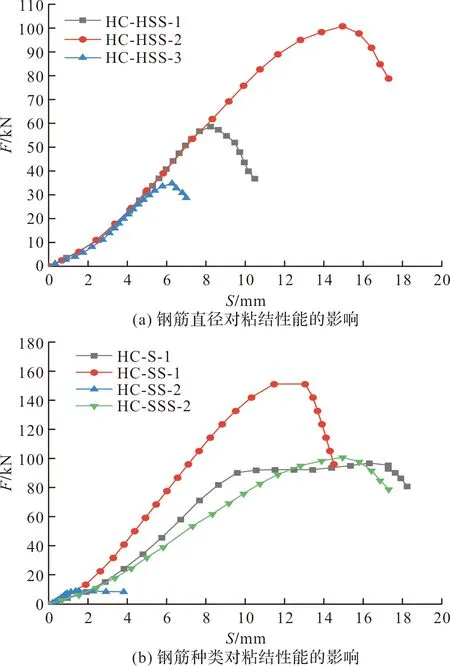
图9 不同参数下的粘结-滑移对比曲线

2.2.1 钢筋直径对粘结性能的影响

钢筋直径越大锚固力越大，但粘结应力基本相同(表4).不同直径的钢筋从UHPC中拔出时，前期的锚固力上升趋势基本一致，如图9(a)所示，钢筋直径越大，锚固力越大，荷载到达到各自峰值的80%时，曲线斜率开始下降，当荷载达到最大值时，钢筋与UHPC试块脱胶，锚固力下降.

2.2.2 钢筋种类对粘结性能的影响

钢筋种类对粘结性能影响较大，如图9(b)所示，四种不同肋壁的变形钢筋中奥氏体不锈螺纹钢筋与UHPC的粘结性能最好，高强不锈钢筋和普通钢筋对UHPC的粘结力试验结果较为接近，但普通钢筋与UHPC脱胶发生在钢筋屈服之后，如果增大普通钢筋的强度，粘结强度增加，光圆钢筋对UHPC的粘结性最差，其粘结强度不足三种螺纹钢筋的10%.

2.2.3 相对保护层厚度对粘结性能的影响

相对保护层厚度对钢筋与UHPC的粘结性能有一定影响，如图9(c)和表4所示.相对保护层厚度由5变为3.75时，其粘结强度由31.98 MPa降至23.54 MPa，粘结强度下降了26.3%，当相对保护层厚度由3.75变为2.5时，其粘结强度由23.54 MPa降至19.69 MPa，粘结强度仅下降了16.3%，因此，随着相对保护层厚度的减小，粘结强度下降趋势逐渐变缓.随着相对保护层厚度的减小，混凝土体难以抵抗钢筋对其施加的环向拉应力，试件的破坏形式由钢筋拔出破坏逐渐转向混凝土劈裂破坏，说明相对保护层厚度的大小决定了试件破坏的形式.

2.2.4 相对锚固长度对粘结性能的影响

如图9(d)和表4所示，增加相对锚固长度，极限拉拔力增大，粘结强度也随之增加.当相对锚固长度由2.5增加至4时，极限拉拔力与粘结强度分别增长113.3%与33.4%；当相对锚固长度由4增加至5.5时，极限拉拔力与粘结强度分别增长69.6%与23.5%.但相对锚固长度增加至5.5时，试件破坏形式为钢筋拔断，极限锚固力大于钢筋的破断拉力，如增加钢筋强度，测试值增长.

2.2.5 配箍率对粘结性能的影响

在UHPC试块中配制箍筋可以有效增加钢筋与UHPC的粘结强度，如图9(e)和表4.没有配制箍筋的试件极限粘结强度为31.98 MPa，箍筋配筋率为0.314%时粘结强度增加至46.48 MPa，涨幅为31.1%，而配箍率从0.314%增加至0.628%时，粘结强度增加至48.25 MPa，涨幅仅为3.8%，随配箍率增大，配箍率对粘结性能的增强效果逐渐减弱，原因是在钢筋拔出时，箍筋可以为核心混凝土提供环向压应力，从而提高核心混凝土的强度.

2.3 粘结滑移本构关系

2.3.1 粘结应力分布

保护层厚度是改变混凝土破坏形式的重要因素[11]，因此为了得到不同相对保护层厚度下锚固段的粘结应力分布，通过钢筋应变计算钢筋应力，进而得到粘结应力，如表5.锚固段不同位置的粘结应力τn可根据式(2)式确定

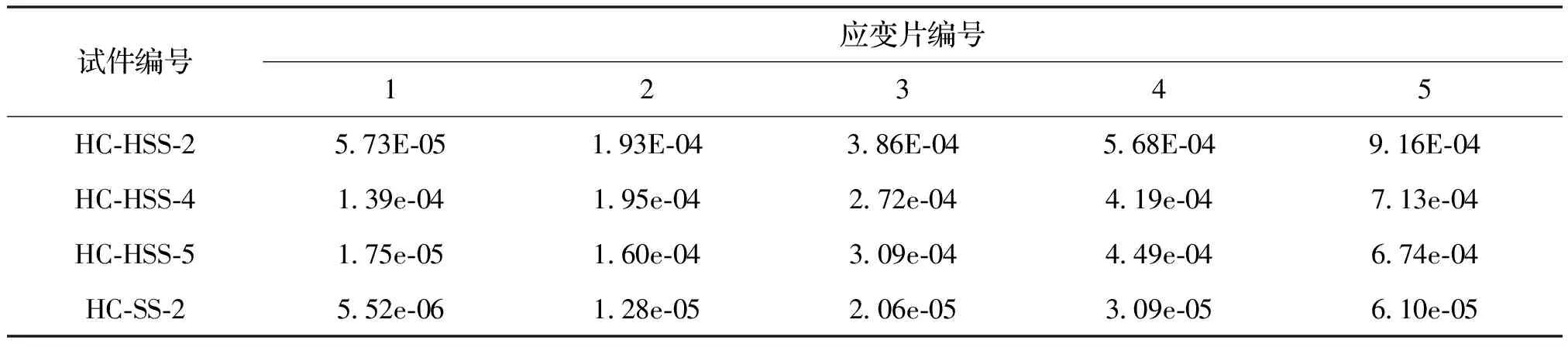
表5 钢筋应变片数值

(2)

式中：τn编号为n的应变片处钢筋与混凝土粘结应力，MPa；σn为第n个应变片处的钢筋应力，MPa；d为钢筋直径，mm；l为两个应变片之间的距离，mm；As为钢筋截面面积，mm2；E为钢筋弹性模量，MPa；εn为第n个钢筋应变的应变.

由图9(c)可知，相对保护层厚度越大平均粘结应力越大，所以HC-HSS-5的平均粘结应力大于HC-HSS-4的平均粘结应力，但由图10所示，在5号应变片位置HC-HSS-4的局部粘结应力反而大于HC-HSS-5，而混凝土劈裂破坏均发生在HC-HSS-4，以此得出局部粘结应力是影响试件破坏形式的因素之一.

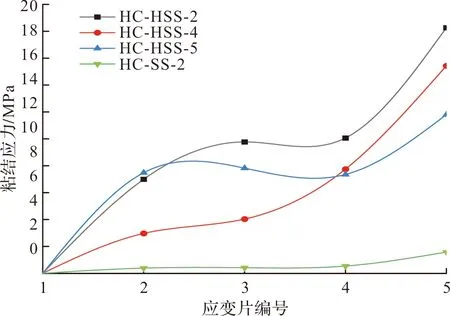
图10 粘结应力分布

2.3.2 本构关系

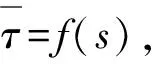
τ=ψ(y)f(s)

(3)

2.3.2.1 平均粘结强度-滑移本构关系

徐有邻等按照粘结滑移曲线特点将普通混凝土粘结滑移本构关系分为五段表达式，每段由各段特征强度和特征滑移值控制，但从曲线的整体走势来看，可简单划分为上升段和下降段两部分，以峰值平均粘结应力对应的位移Su为界，0～Su为上升段，Su之后则为下降段，如式(4).

(4)

式中：τu为峰值平均粘结应力；Su为峰值平均粘结应力所对应的滑移量；α、β为待拟合参数.

对试验曲线进行无量纲化分析后(图11)，用MATLAB软件对式(4)中的α、β进行拟合，得到参数如表6所示.各试件在上升段参数较为统一取值范围在1.01～1.46之间，故取平均值1.20作为α值，即α=1.20；随着相对保护层厚度减小试件破坏形式逐渐由拔出破坏转变为劈裂破坏，故下降段β的取值可根据HC-HSS-2的试验数据拟合得到，即β=12.81.将α=0.120、β=12.81带入式(4)中与各组试件试验曲线的对比如图12.

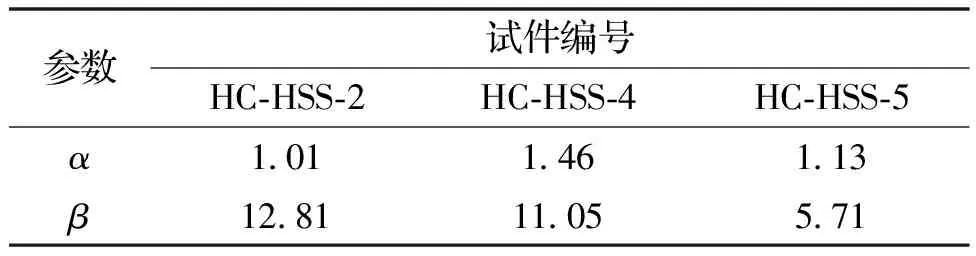
表6 参数对比

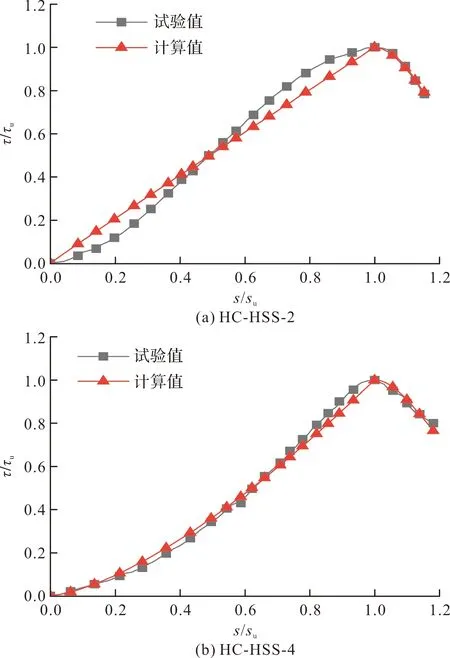
图11 无量纲化后对各曲线参数进行拟合

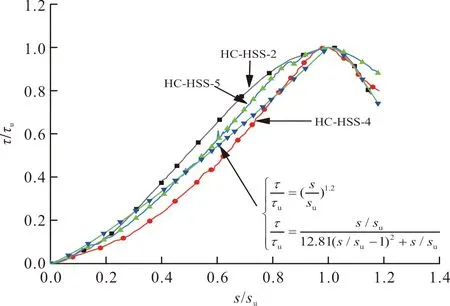
图12 平均粘结-滑移曲线试验值与计算值对比

2.5.2.2 位置函数ψ(y)

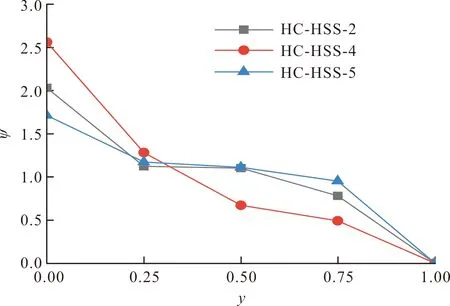
图13 不同锚固位置处粘结强度无量纲化曲线

由上图可知三条曲线走势大致相同，加载端粘结应力最大，距离加载端越远，粘结应力则越小，该位置函数可采用四阶多项式拟合：

Y=a0+a1X+a2X2+a3X3+a4X4

(5)

式中：a0、a1、a2、a3、a4为待拟合参数.

使用ORIGIN软件对式(5)中的参数进行拟合，如表7和图14所示.

表7 位置函数参数拟合值

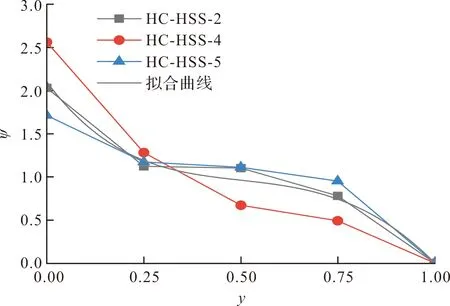
图14 试验曲线与拟合曲线对比

由图14中的拟合曲线可以看出，曲线整体沿锚固段加载端到自由端呈下降趋势，当y值在(0～0.25)和(0.75～1)区间时，下降较快，在(0.25～0.75)区间时下降较平缓.拟合曲线只表示粘结强度沿锚固长度的变化规律，即位置函数ψ(y).结合位置函数曲线特点，自由端和加载端附近粘结强度变化较为剧烈，锚固段中间部分变化平缓，为了工程应用方便，本文提出三折线段模型，如图15.整个模型有四个特征点：A1(0，2)、A2(0.25，1.25)、A3(0.75，0.75)、A4(1，0).

图15 高强不锈钢筋与UHPC粘结滑移位置函数模型

3 粘结强度计算式

通过分析影响不锈钢带肋钢筋与UHPC粘结性能的各项因素，以用BS-R钢筋的试件为例，利用Matlab软件进行统计回归，对普通钢筋混凝土平均粘结应力表达式进行修正，得到不锈钢带肋钢筋与UHPC的平均粘结应力的计算式，如式(5)所示.

τ=(1.27-1.69d/la)(0.85+1.19c/d+5.58ρsv)ft

(6)

式中：ft为混凝土轴心抗拉强度设计值[28]，MPa；ρsv为配箍率.

按照式(6)计算得到粘结强度的计算值τ2与试验值 对比见表8所示.在不同影响参数下，试样的试验值与计算值的比值最大值和最小值分别为1.10和0.90，说明利用修正后的不锈钢筋与UHPC平均粘结应力表达式求得的计算值与试验值吻合较好，可用于计算不锈钢筋与UHPC的平均粘结应力.

表8 平均粘结应力试验值与计算值对比

4 结论

此次拉拔试验共12组36个试件，考虑了影响钢筋与UHPC粘结性能的五种因素，得出以下结论：

(1)本次试验主要破坏形式为钢筋拔出，少量试件存在混凝土劈裂和钢筋拔断；

(2)相对保护层厚度和局部粘结应力影响试件的破坏形式，相对保护层厚度较小或局部粘结应力过高会导致试件劈裂破坏，增加相对保护层厚度可以提高粘结强度；钢筋肋壁的形状尺寸对粘结性能有重要影响；随着相对锚固长度的增加，粘结强度逐渐增大，直到钢筋被拔断；一定的配箍率可以有效提高粘结性能；

(3)粘结应力在锚固段并不是均匀分布的，靠近加载端一侧的粘结应力高于自由端一侧；

(4)对钢筋混凝土粘结强度计算式进行了修正，该计算式可以很好的计算不锈钢筋与UHPC的粘结强度.