双馈风机传递函数的分数阶模型辨识近似

李江，张为庆

（东北电力大学电气工程学院，吉林吉林132012）

0 引言

风能作为可再生能源，已成为全球装机容量最大的绿色能源。双馈风机（doubly-fed induction generator，DFIG）的运行效率高、成本低、变流器容量小，是目前使用最广泛的风力发电机之一[1-6]。当前，我国主要风力发电基地与负荷中心相距较远，需要通过远距离输电线路将电能输送到负荷中心[7-13]，为了提高输电线路的输电能力以及系统的暂态稳定性，通常在远距离高压输电线路中安装串联电容进行补偿，输电线路的串联补偿电容在大规模风电输送中得到了广泛地应用[14-16]，但串联补偿电容的应用同时也给电力系统带来了次同步振荡的风险[6-9]，当前双馈风机次同步振荡的分析主要集中在整数阶领域，在分数阶领域的研究还不够深入。由于转子电磁转矩的变量较多，动态行为比较复杂，对系统次同步振荡的产生具有重要影响，所以本文对双馈风机转子电磁转矩变化量的传递函数增益进行分数阶辨识获取其分数阶模型。

通常采用整数阶模型研究系统的主要特征，但是对于大部分由分布参数构成的系统，整数阶模型并不能全面准确地表达其特性。而与整数阶模型相比，分数阶模型却可以精确地描述分布参数构成的系统[21-23]。随着研究的深入，整数阶模型在分析系统特性时已不足以反映系统的所有特征。分数阶模型虽然可以描述系统更多的特性，但是带来了辨识上的困难，与整数阶模型相比，分数阶模型要综合考虑系数与阶次的关系。在进行分数阶模型辨识时，为了获取最合适、最准确的辨识参数，需要在辨识过程中修改辨识模型，使辨识模型与辨识数据之间的误差最小，利用最优化的方法解决模型辨识问题[24]。

分数阶微积分理论在实际工程中也有比较广泛地应用，电感与电容的分数阶模型比整数阶模型更能准确体现元件特性[25-28]。目前主要有频域和时域两种辨识方法，频域辨识方法根据频域数据，通过辨识算法得到分数阶模型，时域辨识方法则通过时域数据进行辨识，与频域辨识相比，时域辨识方法的辨识时间长、计算量大。文献[29-30]根据永磁电机的电路特性建立了其分数阶模型，并设计了永磁风机的时域与频域实验方案，辨识得到了永磁风机的分数阶模型，通过对比分析验证了分数阶模型的准确性；文献[31]利用实验辨识得到了锂电池的分数阶等效电路模型，通过分析模型预测结果与实验结果，验证了锂电池的分数阶模型的准确性。

本文首先在第1 节中给出双馈风机转子侧电磁转矩传递函数增益的推导；然后，在第2 节中介绍基于Levy 方法的改进频域辨识算法[32-33]，在第3节将辨识算法应用到双馈风机转子侧传递函数增益的分数阶模型辨识中，并通过Bode 图和单位阶跃响应曲线的分析验证了分数阶模型的准确性。

1 双馈风机模型与转子电磁转矩传递函数增益

双馈风机主要由风力机、传动系统、转子侧变流器（rotor side converter，RSC）与网侧变流器（grid side converter，GSC）等部分组成，本文所研究的系统如图1 所示。在表1 中给出双馈风机及输电系统的参数。

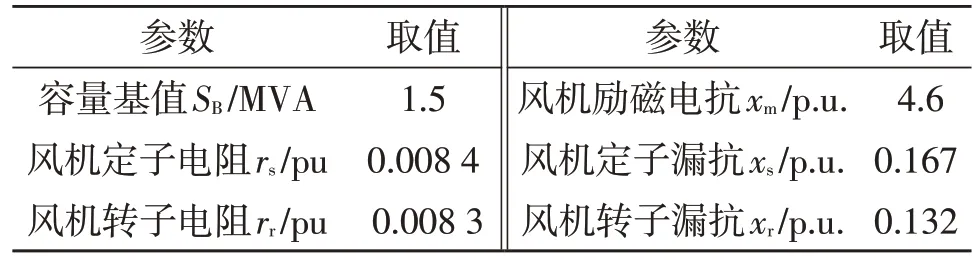
表1 双馈风机和输电系统的参数Table 1 Parameters of DFIG and transmission network

图1 双馈风机系统示意图Fig.1 Schematic diagram of doubly fed induction generator system

转子感应电动势的变化量公式为[34]

式中：ωr0*是稳态时转子转速的标幺值；Lm*为dq坐标系下的定转子之间的互感标幺值；isd0*、isq0*为定子电流在d轴和q轴分量的标幺值；ωs*为定子电角频率；ωBase是同步角频率；Δωr*是转子转速的变化量。

根据双馈风机系统示意图中风机转子及RSC部分的电路结构，并通过Laplace 变换可得到两相旋转坐标系下的方程表达式为

式中：Lcr*是转子侧变流器连接的电抗标幺值；Rrcr*=Rr*+Rcr*，即将转子电阻与RSC 电阻合并后的电阻标幺值；ωBase是同步角频率；ωr*为转子转速的标幺值；ΔErd*、ΔErq*分别是转子d、q轴感应电动势变化量的标幺值；ΔIrd*、ΔIrq*分别为转子电流的d、q轴分量标幺值；ΔUrd*、ΔUrq*分别是RSC 在d、q轴上输出电压变化量的标幺值。

在转子侧变流器的控制策略中，直轴和交轴均采用内环和外环控制，如图2 所示。直轴控制是为了确保转子的转速能够跟随参考值，交轴控制是为了实现定子的无功功率跟随参考值。

图2 RSC控制策略Fig.2 RSC control strategy

在下文的分析中，考虑到转子侧变流器的内环系数远小于外环系数，所以只考虑内环系数。当转速发生变化时，转子侧变流器输出电压的变化量公式为

式中，Kp2、Ki2分别是转子侧变流器的内环比例、积分系数。

联立式（1）-（3），即可得到转子电流变化量与转速变化量之间的关系式公式为

根据双馈风机的电磁转矩关系式，可以得到转子转矩变化量的表达式为

式中，GTer(s)是转子电磁转矩变化量传递函数增益。

大多数的风电场为了补偿无功功率常装设静止补偿器或静止同步补偿器，所以双馈风机的定子电流中只含有isd0*，而isq0*=0。所以，可以得到转子转矩的表达式为

式中，各次系数公式为

2 基于Levy的分数阶辨识算法

假设对于公式（6），通过Levy 辨识算法辨识得到的分数阶模型表达式GF(s)公式为

第1 步：为了得到公式（7）中的各个参数，得到公式（7）所表示的分数阶模型的频域特性表达式。

令s=jω，带入分数阶模型表达式中，其频域特性表达式为

第2 步：利用系统模型G(s)与辨识模型之间的误差建立目标函数，求取分数阶模型中的各个参数。

误差目标函数公式为

当误差目标函数η(jω)取值最接近0 时，GF(s)即为满足条件的分数阶模型。但是如果直接利用公式（9）的表达形式求解目标函数难以获取分数阶模型中的各个参数，所以需要对公式（9）进一步进行转化，得到公式

将公式（8）带入公式（10），得到公式

为了求解分数阶模型中的辨识参数aj（j=0，1，2，…，n）和bi（i=0，1，2，…，m），将JL=|E|2作为目标函数，分别对aj和bi求偏导，公式为

将公式（11）带入公式（12）中，可得方程组

通过求解公式（13）和公式（14）所表示的方程组就可以得到分数阶模型的辨识参数aj（j=0，1，2，…，n）和bi（i=0，1，2，…，m）。为了更清楚简洁地表达公式（13）和公式（14），用矩阵进行表示，公式为

式中：A、B、C、D、E和G的表达式在引入权重wp函数之后给出，见公式（18）-（23）；a=[a0，a1，a2，…，an]T；b=[b0，b1，b2，…，bm]T。

第3 步：为了提高辨识得到的分数阶模型的精确性，利用Vinagre 算法构造新的目标函数，并给出分数阶模型与系统模型的均方差指标（root mean square error，RMSE）。

对于目标函数JL，频率ω的取值越大，频率ω对目标函数JL的影响就越大，而当频率ω的取值较小时，频率ω对目标函数JL的影响也较小，这就使得分数阶模型在低频段内辨识效果不够理想。本文采用Vinagre 算法：按顺序将wp函数添加到原目标函数JL中，提高辨识算法在低频区间的辨识准确度，引入wp函数之后的目标函数JV为[35]：

从公式（16）和公式（17）中可以看出，低频对目标函数的影响得到了提高。因为wp函数与系数aj和bi无关，所以不会对公式（12）的值产生影响。加入wp函数之后，公式（15）中各个参数的表达式为

RMSE 的表达式为

式中，f是采样点的总数。

3 算例分析

3.1 分数阶模型的辨识

本文依据分数阶连续分布的概念，提出双馈风机转子电磁转矩传递函数增益的两种分数阶模型表达式[36]：

第1 种分数阶模型设置为m=n=2，称为2q阶分数阶模型，该模型是为了让表达式更加简洁、直观的表现出分数阶模型的优势，还可以在后续分析转子特性时将其与分数阶电路相对应，用分数阶理论分析系统特性。

第2 种模型将m和n分别设为3 和4，称为3q阶分数阶模型，该模型是依据第1 节中双馈风机转子电磁转矩的整数阶传递函数增益的形式设定的。当q=1 时，该模型等价于整数阶模型在数值上的表达式。

根据第1 节推导的双馈风机转子电磁转矩传递函数增益的表达式，做出转子传递函数增益的Bode 图，并从图中取52 个有代表性的频率点作为辨识数据；然后利用第2 节的辨识算法对2q阶分数阶模型和3q阶分数阶模型进行参数辨识。图3 是频率在[0.1 rad/s，316 rad/s]范围内52 个频率点的辨识数据。

图3 频域辨识数据Fig.3 Frequency domain identification data

本文设定f=52，分数阶阶次q取值区间为（0，2），取值间隔为0.01。根据第2 节中提出的基于Levy 的改进辨识算法，利用矩阵公式（15）可以计算出2q阶分数阶模型中的参数a1、a2和b0、b1、b2以及3q阶分数阶模型中的参数a1、a2、a3、a4和b0、b1、b2、b3，并利用公式（24）计算相应模型的均方差值。

对于2q阶分数阶模型，当n=m=2、q=0.99 时，均方差值为RMSE=1.030 9×10-4，得到双馈风机转子电磁转矩传递函数增益的2q阶分数阶模型辨识公式为

同理，对于3q阶分数阶模型，当n=3、m=4、q=0.51 时，最小均方差的值RMSE=5.856 2×10-5，双馈风机转子电磁转矩传递函数增益的3q阶分数阶模型公式为

3.2 分数阶辨识的频域结果分析

为了验证本文方法的有效性，将得到的两种分数阶模型与辨识数据模型进行对比，图3 和图4 是其对比Bode 图。从图中可以看出，在风机实际运行使用的频率区间内，根据辨识结果的均方差指标以及在图像上的直观拟合效果可以看出，两种分数阶模型与辨识数据模型之间误差小，拟合度高。因此，对双馈风机的转子电磁转矩进行分数阶频域建模是正确有效的。

图4 分数阶模型与辨识模型的对比Bode图Fig.4 Bode diagram of comparison between fractional models and identification data

3.3 分数阶模型的阶跃响应分析

3 种模型下的单位阶跃响应曲线如图5 所示，从图中可以看出，3 种模型在单位阶跃信号的作用下，其输出响应从初始状态到稳态的过程中，单位阶跃响应的曲线是衰减震荡的欠阻尼形式。表2 为3 种模型在单位阶跃响应下的性能指标，表3 为采用单因素方差分析的结果，用以分析2q阶分数阶模型G1(s)、3q阶分数阶模型G2(s)与辨识数据模型G(s)之间的拟合程度和暂态特征上的有效性。

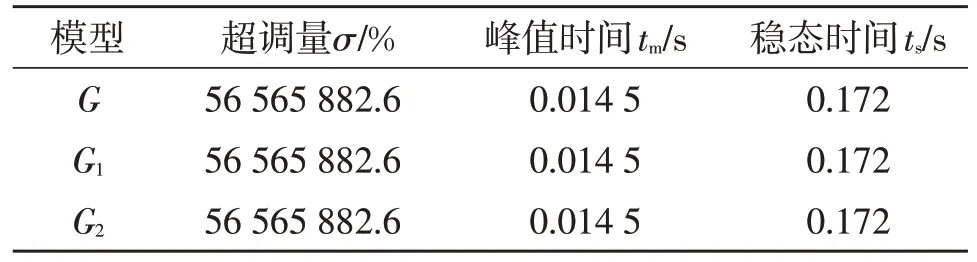
表2 3种模型在单位阶跃响应下的性能指标Table 2 Performance indicators of the three models under unit step response

表3 单因素方差分析结果Table 3 Results of one-way ANOVA

图5 两种分数阶模型与辨识数据模型的阶跃响应Fig.5 Two fractional order models and step response of identification data model

阶跃响应的性能指标主要包括稳态时间ts、峰值时间tm和超调量σ，如表2 所示，3 种模型的性能指标在数值均相等，这表明两种分数阶模型与辨识模型之间的拟合程度很高。为了更加准确的验证3 种模型之间拟合的精度，下文采用单因素方差分析进行验证。

单因素方差分析是指试验中只有一个因素发生变化时对试验数据进行分析，通过检验方差相等的多个正态总体均值是否相等，判断变化的因素对试验指标是否有显著影响。在分析分数阶模型与辨识数据模型的单位阶跃响应时，变化的因素就是不同分数阶模型与辨识数据模型的分组。通过分析不同模型分组的单因素方差分析结果，判断是否有显著差异。利用数值分析工具箱进行此项分析，分析结果如表3 所示。

首先对表3 中参数的意义进行解释说明，模型组中的G-G1和G-G2分别是辨识数据模型G（s）与2q阶分数阶模型G1（s）和3q阶分数阶模型G2（s）的分组；Average 是两组数据差值的平均值；F是检验统计量；P-value 是观测差异的显著水平；F-crit 是检验临界值，当F0.05 时，表示没有显著差异。

在单因素方差分析过程中，可信度设置为95%。从表3 中可知，两个模型组的观测差异的显著水平P-value 大于0.05 与检验统计量F小于检验临界值F-crit，表示2q阶分数阶模型G1（s）和3q阶分数阶模型G2（s）取得了较好的拟合效果以及在暂态特征上取得了有效的结果；并且辨识数据模型G（s）与3q阶分数阶模型G2（s）的P-value 更大、F更小，说明3q阶分数阶模型的拟合度更高。

4 结语

基于频域辨识数据对双馈风机的转子电磁转矩传递函数增益进行了分数阶辨识近似，根据不同的情况，采用基于Levy 的改进辨识算法，在频域中实现了对所提出的2q阶分数阶模型和3q阶分数阶模型的参数辨识。Bode 图的对比结果和均方差数值指标均验证了所提出的两种分数阶模型与原模型频域的近似性。单位阶跃响应的性能指标和单因素方差分析的结果验证了分数阶模型对原整数阶模型在暂态特征上的有效性。