孤岛运行方式下柔性直流配网高次谐波谐振及抑制措施研究
李书亚,解绍锋,马智泉
(1.西南交通大学电气工程学院,成都 610041;2.国网浙江省电力有限公司电力科学研究院,杭州 310014)
0 引言
近几年来,随着柔性直流输电技术的日益成熟,由此衍生的柔性直流配电方式因其能从根本上解决交流配电系统在运行效率和供电可靠性等方面的问题得到了广泛使用[1-2]。作为连接直流电网和交流电网的关键电力电子设备—模块化多电平换流器(modular multilevel converter,MMC)已经在柔性直流输电系统中得到了广泛应用,与传统电压源型换流器相比,MMC 换流器对开关器件耐压值的要求比较低,但在实际工程应用中,MMC 换流器仍会产生含量较高的低次谐波与高次谐波带[4-6]。在孤岛运行方式下,当MMC 换流器所产生的谐波次数与由输电电缆、换流器桥臂电抗器和负载组成的小系统的自然谐振频率重合时,就会产生谐波谐振,严重影响交流侧母线的电能质量,危害交流母线侧各种电气设备的安全稳定运行[2]。在当前运行的实际柔性直流配电工程中,已出现了多起电力电子设备与电力系统谐波谐振的问题:1)2018 年在某柔性直流配电网的换流器交流并网侧发现了严重的47 次高次谐波谐振现象,导致10 kV 交流配网系统上潜在1 kV 左右的高频过电压[1];2)2020 年某海上风电工程发生11 次谐波谐振,并在陆上计量站注入电网并网点处检测到11 次谐波电流含量严重超出国标限值。
关于柔性直流配网系统中高次谐波谐振问题的研究,文献[2]通过建立孤岛运行方式下换流器-输电电缆-负荷组成的小电力系统的数学模型,对高频谐波谐振传递的内在机理进行了简单的分析研究,但并未提出具体的解决措施。文献[4]对柔性配电网系统中换流设备—MMC 换流器在作为逆变器时的谐波特性进行了分析,为柔性配电网系统谐波谐振问题的探究奠定了基础。文献[7]在分析了传输电缆实际阻抗模型特征的基础上提出了通过Taylor 近似对传输电缆阻抗模型进行线性化的方法,此方法可以提高电缆阻抗模型的准确性。文献[8]通过建立柔性输电电缆分布参数模型,分析了新能源并网接入点电压谐波引起的电缆线路谐波谐振问题。文献[9-12]对风力发电谐波谐振问题进行分析,文献[9]主要介绍了风力发电系统中由谐波谐振引起的电能质量问题。针对海上发电厂的谐波谐振问题,文献[11-12]通过建立海上风电场的谐波模型和海底电缆分布参数模型基于敏感度对风力发电系统谐波谐振行为进行了探究。
关于柔性直流配网中高次谐波谐振抑制的研究,文献[8]提出一种谐波电流指令生成的控制方法,该方法可以使分布式能源并网逆变器交流侧在连续的谐波频率上呈现纯阻性,避免谐波谐振的发生从而达到抑制谐波谐振的目的。针对风力发电场的谐波谐振问题,文献[10]提出一种由无源滤波器和有源滤波器组成的混合无源滤波器,文献[12]提出利用频移来抑制谐波谐振,文献[13-14]提出了一种可抑制未知频率下多重谐波谐振的有源阻尼滤波器。针对含多电压源型换流器配电网的高频谐波谐振问题,文献[15-16]提出采用载波相位协调法抑制高次谐波谐振问题,文献[17]提出等效增大换流站输出阻抗支路谐波电阻的方法,全面扼制换流站输出阻抗支路谐波电流,以达到谐波谐振的主动抑制,但上述该方法实现起来难度较大。
综上所述,目前已有不少国内外学者投入到了柔性直流配电网系统谐波谐振问题的研究,但针对孤岛运行方式下模块化多电平换流器柔性配电网高次谐波谐振及其抑制措施的研究比较欠缺。因此,本文基于电缆的分布参数模型建立模块化多电平换流器柔性直流配网的数学模型,并对孤岛运行方式下柔性直流配网系统高次谐波谐振特征进行理论分析,然后基于PSCAD/EMTDC 仿真软件建立柔性直流配网的仿真模型,并通过实测数据对仿真模型的准确性进行验证,最后验证了所提出的适用于柔性直流配网混合无源滤波器的有效性。
1 孤岛柔直配网谐波特性研究
1.1 MMC换流器谐波特性
典型MMC 换流器的结构图见图1。
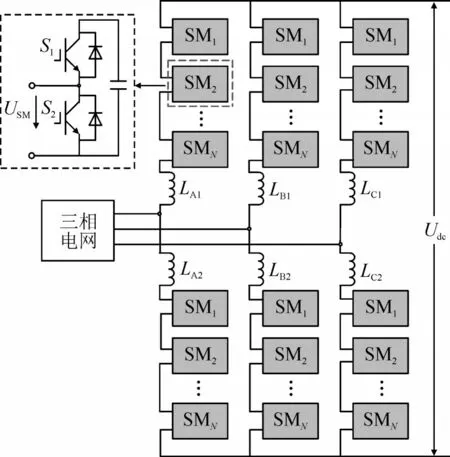
图1 MMC换流器结构图Fig.1 Structural diagram of MMC converter
图中系统每相都由上桥臂和下桥臂两部分组成,每个桥臂上的子模块单元数量和类型全都相同,并通过桥臂电抗器将上下桥臂连接起来。基于最近电平逼近调制(NLM)的MMC 换流器,就是通过各级联子模块单元输出电压的叠加来逼近调制波电压值的换流器。
孤岛运行下,MMC 换流器实现逆变功能,MMC换流器的谐波特性主要由子模块单元输出电压的谐波特性所决定,求解出子模块输出电压表达式以及子模块的投切数量,通过叠加原理即可求得整个换流器的输出电压表达式。由文献[1]可以得到基于NLM 调制的MMC 换流器输出电压表达式为
式中:UC为子模块电容电压;h为谐波次数;θi为第i个电平开始投入的电角度;N为电平数量。
根据输出电压表达式可知:理想情况下,输出电压仅含有奇次谐波分量而不含偶次谐波分量。根据换流器输出电压表达式,求出21 电平MMC 换流器输出电压谐波特性如图2 所示。
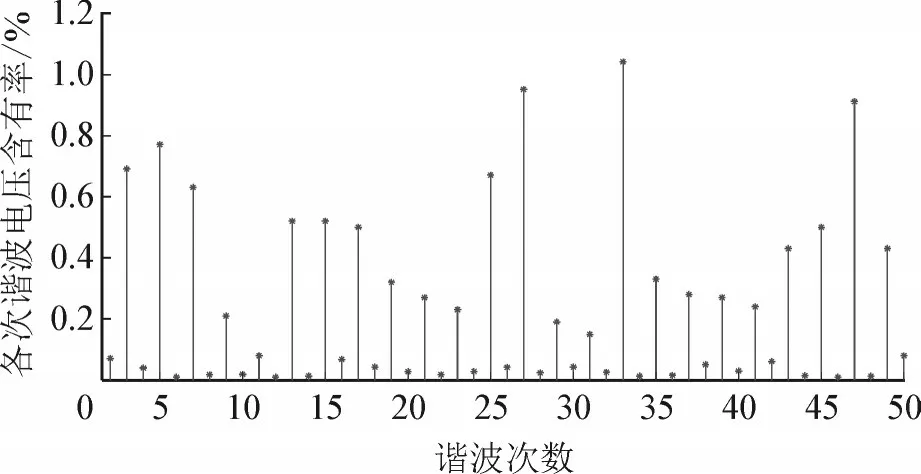
图2 N=21时MMC换流器输出电压频谱Fig.2 Output voltage spectrum of MMC converter at N=21
1.2 孤岛柔性直流配网谐波谐振特征分析1.2.1 电缆分布参数模型
电缆模型分为集中参数模型和分布参数模型两大类,鉴于本文分析的是较高频率的谐波信号,且频率范围较大,需要考虑分布参数对高频率谐波的影响,故采用电缆的分布参数模型来进行电缆模型的等效。电缆分布参数等效电路见图3。

图3 电缆分布参数等效电路Fig.3 Equivalent circuit of distribution parameter of cable
根据均匀传输线理论,电缆任一处无限小长度dl都有阻抗Z0hdl和导纳Y0hdl,如图3 所示。
当电压UB和电流IB已知时,则:
式中:Zch为h次谐波时电缆线路的特征阻抗;γch为h次谐波时线路传递系数;l为电缆长度。
将电缆线路作为无源的双端口,则电缆线路双端口网络方程为
将上述双端口网络用π 型电路进行等效,等值电路的参数与传输参数的关系为
又因为Zch=Z0h/γh=γh/Y0h,所以上式可表示为
式中:Kz、KY为π型等值电路阻抗和导纳的修正系数[19]。电缆线路可以等效为如图4 所示的π 型等效电路。
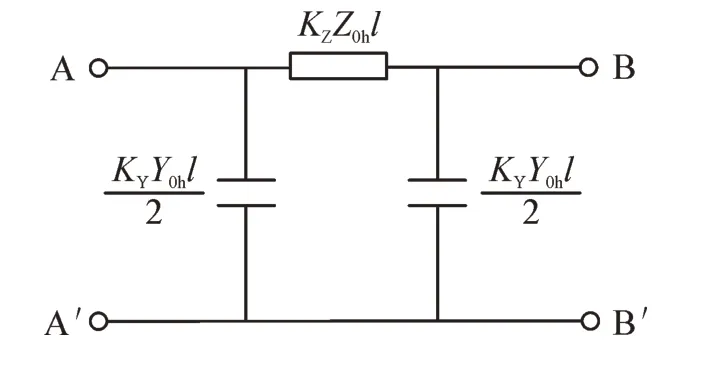
图4 电缆π 型等效电路Fig.4 Type π equivalent circuit of cable
1.2.2 柔性直流配网等效数学模型
将MMC 换流器等效为谐波电压源与桥臂等效阻抗串联的形式作为其数学模型,电缆模型按如图4 所示的π 型等效电路进行等效,建立的柔性直流配网谐波计算等效电路如图5 所示。图中:ZLh为负荷的等值阻抗;ZLh为电网等值谐波阻抗。
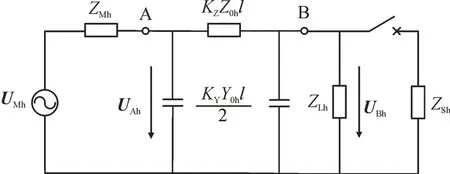
图5 柔性直流配网谐波计算等效电路Fig.5 Equavilent circuit of harmonic calculation of flexible DC distribution network
孤岛运行方式下有
孤岛运行方式下,将图5 等效为如图6 所示的柔性配电网系统等效电路。

图6 柔性直流配电网谐波计算等效电路Fig.6 Equivalent circuit of harmonic calculation of flexible DC distribution network
图中:
1.2.3 柔直配网谐波谐振特征分析
分析柔性直流配网系统谐波计算等效电路和电路知识可知,MMC 换流器输出电压公式为
式中,KBh=,
定义谐波电压增益KFDh公式为
由于Z1h为容性阻抗,ZMh为感性阻抗,当h满足|Z1h+(1-KBh)ZMh|≈0 就会产生谐波放大现象,此时的KFDh>1。
孤岛运行方式下,结合谐波电压增益的数学表达式利用Matlab 编程软件计算出的主要谐波次数下柔性配电网系统母线谐波电压增益KFDh见图7。
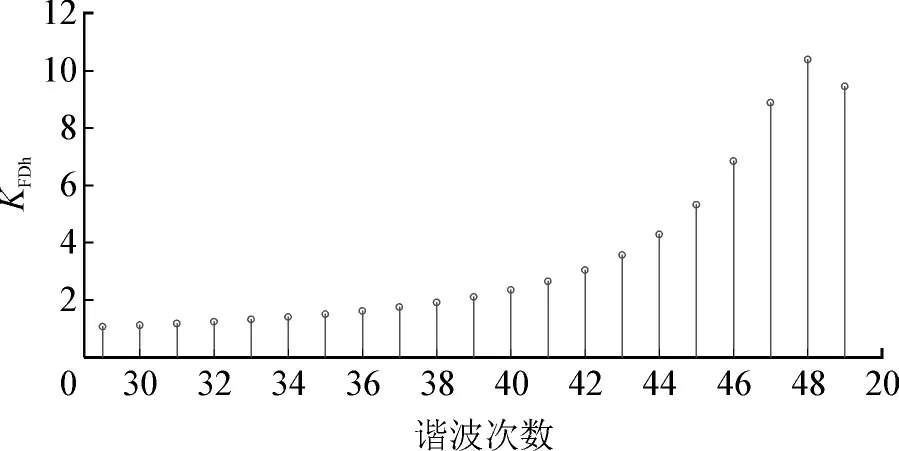
图7 主要谐波次数电压增益计算值Fig.7 Calculation value of voltage gain of main harmonic number
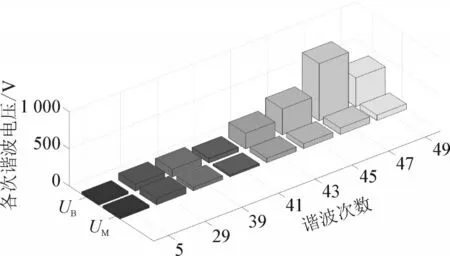
由图可知,KFDh最大值时对应的谐波次数为48 次,母线侧各次谐波电压含有率实测值见图8。根据图8 所示母线侧各次谐波电压含有率实测数据显示,孤岛运行方式下,该柔性配电网系统母线侧主要谐波电压为45 次(4.21%)、47 次(7.32%)、49 次(5.50%)。考虑到MMC 输出电压中偶次谐波电压含量较低,且换流器输出的47 次谐波含量比48 次附近其它奇次谐波含量大,故48 次临近的奇次47 次谐波为主导谐波,计算结果与实测数据的谐振中心相同。
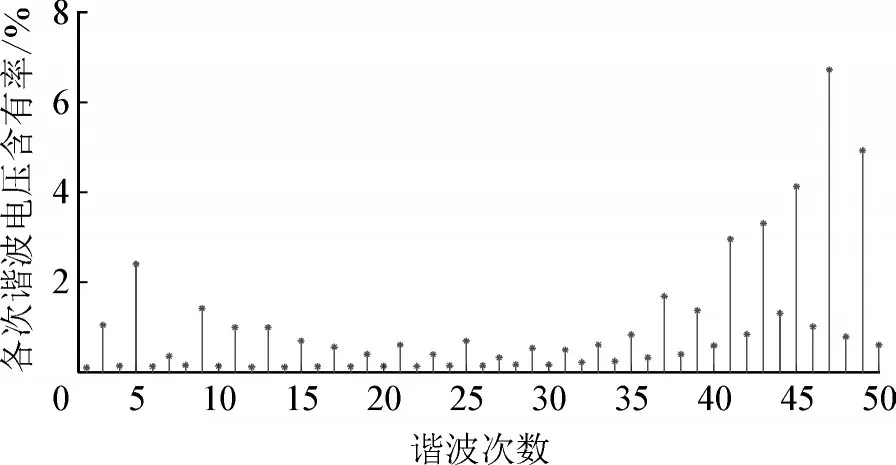
图8 母线侧各次谐波电压含有率实测值Fig.8 Actually measured values of harmonic voltage contents at bus side
2 谐波谐振抑制技术
2.1 混合无源滤波器原理
对实测数据进行FFT 分析可知,换流器对侧母线电压除了含有丰富高次谐波外,5 次谐波的含量也较高。针对柔性配电网系统交流母线侧谐波特性,这里采用单调谐滤波器与阻波高通滤波器组成的混合无源滤波器,其原理图如图9所示。

图9 混合无源滤波器原理图Fig.9 Principle diagram of hybrid passive filter
混合无源滤波器的阻抗频率特性曲线见图10。由图10 可知,基波时,滤波器等效阻抗保持在一个较大值,因此滤波支路不消耗基波功率;5 次谐波时,滤波支路等效阻抗接近于0,对应滤除系统中含量较高的5 次谐波;高次谐波时,滤波支路等效阻抗保持在一较小值,为高次谐波带提供滤波通路。
The experimental results of Scenario 1 are given in Table 3 and Fig.5.From them,the following should be noted:
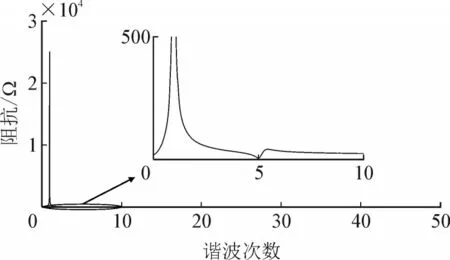
图10 混合无源滤波器阻抗频率特性曲线Fig.10 Impedance frequency characteristic curve of hybrid passive filter
2.2 混合无源滤波器谐振抑制理论分析
孤岛运行方式下,谐振主要发生在由换流器、电缆和负荷组成的小系统中,从换流器往母线侧负荷方向看,换流器、输电电缆和负荷组成的小系统可以看成一端口网络,等效电路如图11 所示,UMh为等效谐波电压源,ZMh为换流器桥臂等效阻抗,ZLh为负载等效阻抗,ZLVh为混合无源滤波器等效阻抗,Ih为流向母线侧的谐波电流,ILVh为流向滤波器的谐波电流,ILh为流向负载的谐波电流。
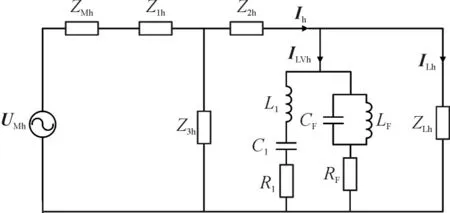
图11 投入滤波器后的柔性配网系统等效电路图Fig.11 Equivalent circuit diagram of flexible distribution network system after switching of filter
将流过滤波器的谐波电流与总谐波电流相除并取模值,可得到h次谐波下滤波器的谐波系数KLVh公式为
同理,h次谐波下负载阻抗的谐波系数KLh公式为
当KLVh=0,KLh=1 时,滤波器的滤波效率为0;当KLVh=1,KLh=0 时,滤波效果最为理想;当0
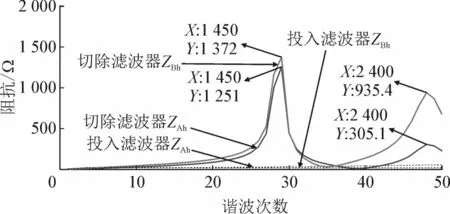
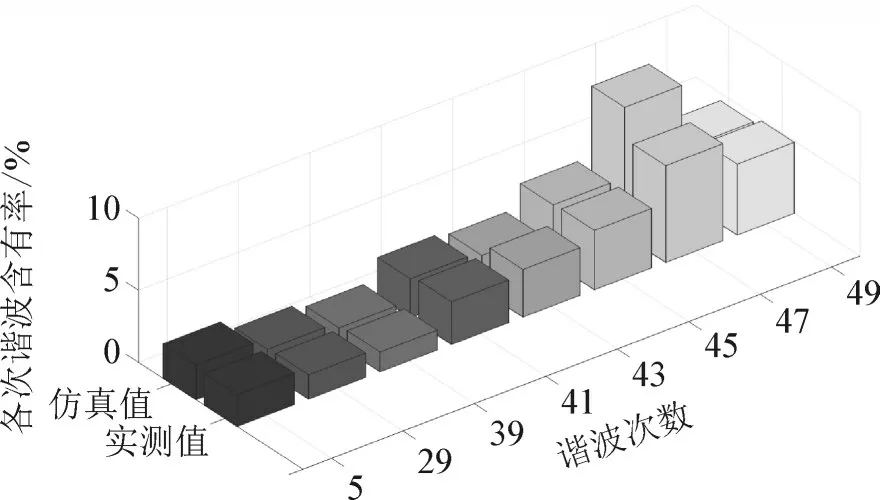
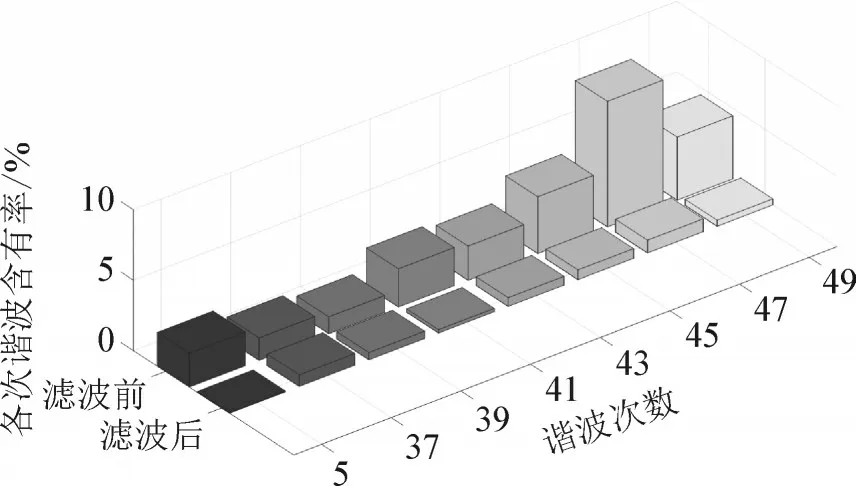
滤波器的投入不仅会起到滤除谐波电流的作用,同时还会改变系统的谐振特性。记从B 点看的系统等效阻抗为ZB(ω),其原始谐振频率为ωc,则有ZB(ωc)→∞。投入滤波器后有Z′B(ω)=ZB(ω)//ZLV(ω),在原始谐振频率ωc下有Z′B(ωc) 基于PSCAD/EMTDC 仿真软件对柔性配电网系统进行仿真建模时要对电缆模型进行选取,选取PSCAD/EMTDC 仿真软件中能准确地描述电缆在较大频率范围内特性的频率相关线路模型,建立一种只需输入电缆走廊的几何参数就可以建立电缆模型[20-22]。根据实际工程中的电力电缆实际参数和横截面的结构,并经过合理的抽象和等后,建立的电力电缆横截面参数如图12 所示。 图12 电力电缆模型的截面示意图Fig.12 Sectional schematic diagram of power cable model 本文主要研究对象是孤岛运行方式下由换流器、输电电缆和负荷组成的小系统的高次谐波谐振问题。负载等效为感性阻抗模型,电缆选取精确度较高的Phase 模型来建立,建立的柔性直流配电网的仿真模型如图13 所示。 图13 柔性直流配网PSCAD/EMTDC仿真等效模型Fig.13 Equivalent model of PSCAD/EMTDC simulation of flexible DC distribution network 3.2.1 投入滤波器前后系统阻抗频率特性分析 图14 投入滤波器前后柔性配电网阻抗频率特性曲线对比Fig.14 Comparison of impedance frequency characteristic curves of flexible distribution network before and after switching of filter 由图14 柔性配电网阻抗频率特性曲线的对比可知,投入滤波器前,无论是从A 点还是B 点进行测量,得到的柔性配电网系统阻抗频率特性曲线都有两个峰值,分别对应两个谐振点:1 450 Hz 和2 400 Hz。投入混合无源滤波器之后,柔性配电网系统原有的谐振点被消除,避免了谐波谐振的发生,提高了系统的电能质量,与理论分析结果一致。 换流器输出电压与母线侧电压对比见图15。从图15 可知,在h=29 时,UM29≈UB29,则KFD29≈1,无谐波放大效果;在h=48 时,UM48 图15 换流器输出电压与母线侧电压对比Fig.15 Comparison between the output voltage of converter and the voltage at the bus-side 3.2.2 投入滤波器前后系统谐波特性分析 实测数据分析可知,柔性配电网母线侧电压高次谐波主要集中在37-49 次之间,并且谐波电压总畸变率达到11.89%,为验证仿真模型的准确性,将谐振中心附近各次谐波电压含有率的实测值与仿真值进行对比,见图16。 图16 谐振中心附近各次谐波电压含有率计算值与仿真值对比Fig.16 Comparison of calculated and simulated values of each harmonic voltage ceontents near the resonance center 孤岛运行方式下,谐振中心附近各次谐波电压含有率仿真值与实测值接近,谐振中心附近各次谐波含有率分布趋势一致,仿真模型中换流站对侧并网点母线谐波电压总畸变率为11.99%,与实测值11.89%接近,从而可以验证仿真模型的准确性。基于建立好的仿真模型,将滤波器投入到柔性直流配网系统中,对母线侧电压进行FFT 分析,见图17,并对系统中主要谐波次数的滤波率进行计算,得到主要谐波次数的滤波率,见表1。 图17 滤波前后谐振中心附近各次谐波电压含有率对比Fig.17 Comparison of each harmonic voltage contents near the resonance center before and after filtering 孤岛运行方式下,在投入混合无源滤波器之后,柔性直流配电网母线侧电压波形得到改善,高次谐波电流基本被滤除,谐波电压总畸变率由11.96% 降低为0.83%,满足国标限值要求[21]。无论是对5 次谐波,还是对高次谐波带,混合无源滤波器的滤波率均能保持在一个较高水平,由此说明混合无源滤波器可以兼顾单调谐滤波器与阻波高通滤波器的滤波特性,仿真结果与理论分析一致。 本文就孤岛运行方式下柔性直流配电网高次谐波谐振问题,通过建立数学模型和仿真模型对柔直配网系统的谐波谐振特性进行了分析,得出如下结论: 1)通过搭建孤岛运行方式下基于电缆分布参数模型的柔性直流配电网等效数学模型,推导出了能够直接确定柔性直流配电网系统有效谐振点的谐波电压增益数学表达式,为柔性直流配电网谐波谐振特性提供了一种有效的分析方法; 2)基于PSCAD/EMTDC 仿真平台搭建基于电缆Phase 模型的柔性直流配电网仿真模型,在对仿真模型阻抗频率特性进行分析时发现系统中存在两个谐振点,通过两谐振点的谐波电压增益KFDh确定出了系统的有效谐振点,且仿真分析结果与理论计算结果一致,证实了谐波电压增益数学表达式与仿真模型的有效性; 3)通过实例分析验证了谐波电压增益通用数学表达式和仿真分析的准确性,并基于仿真模型验证了混合无源滤波器不仅能有效滤除系统中高次谐波带以及特定次数的低次谐波还会改善系统阻抗频率特性的结论,为混合无源滤波器在柔性直流配网中的广泛应用提供参考。3 孤岛柔性直流配网系统谐振抑制仿真分析
3.1 孤岛柔性直流配网系统仿真模型

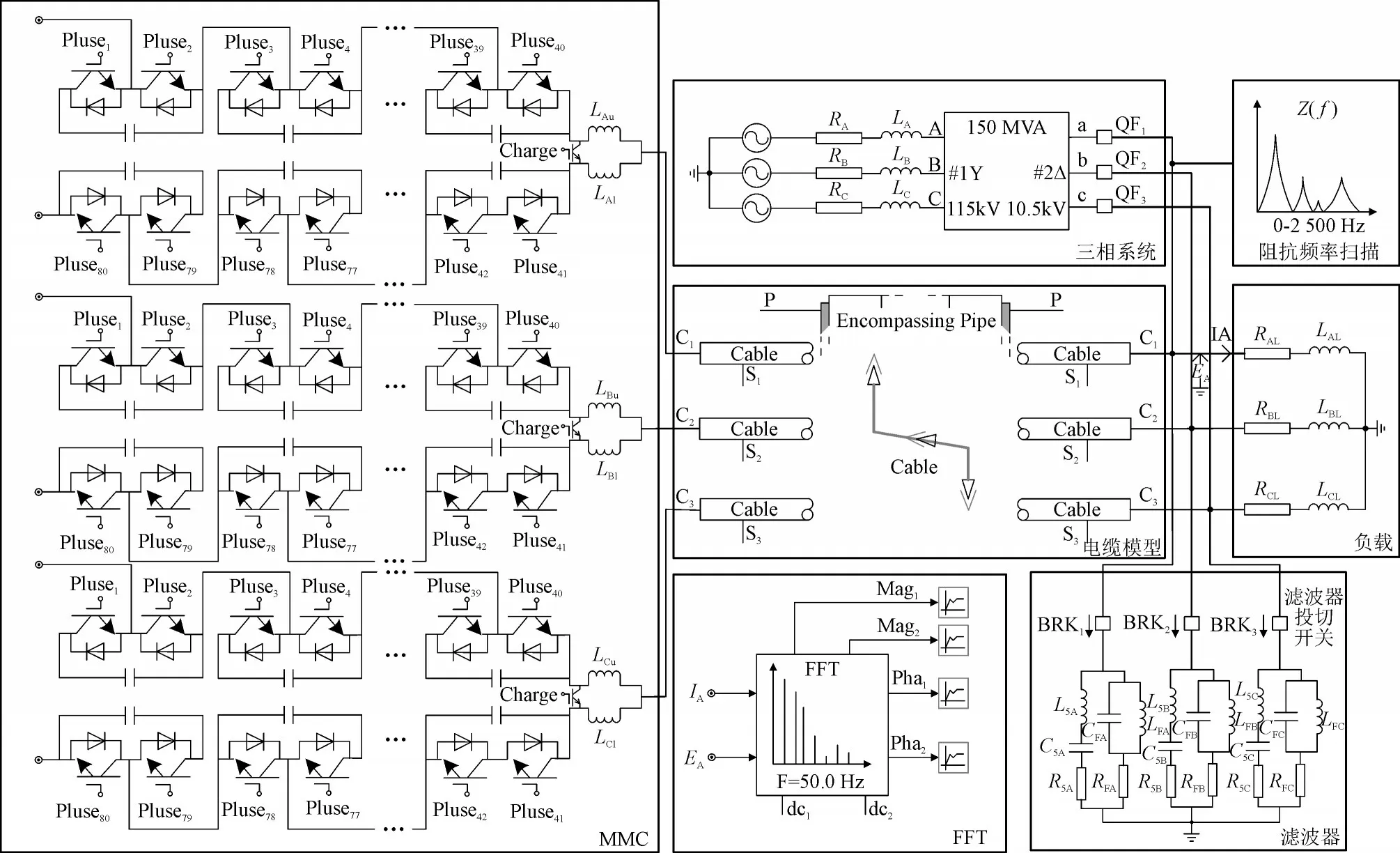
3.2 投入滤波器前后系统谐波谐振特性分析
4 结语

