薄膜电容器ESL 研究分析

王祥，徐佩，江龙祥，盛健

（安徽铜峰电子股份有限公司，安徽铜陵 244000）

0 引言

薄膜电容器具有寿命长、损耗小、选择负温度系数介质（如聚丙烯薄膜）时内部温升小等特点[1-4]，各方面性能优异，从事电容器行业的工作者和使用电容器的用户鲜少提及和要求电容器的等效串联电感[5]（equivalent series inductance，ESL）这一性能指标。大多数电容器（如交流马达启动[6-7]、运行电容和一般滤波电容等）使用在低频工况，这些电容器在低频时感抗基本为零，ESL 完全可以忽略不计。随着电力电子电容器广泛应用，功率半导体器件[8]的开关频率较高，如IGBT 的工作频率可达到40～100 kHz，高频电容低ESL 也就成为电容器行业用户关键需求指标。

1 ESL模型

薄膜电容器工作在高频时阻抗模型见图1，阻抗[9]计算见式（1），随着频率的增加，阻抗（容抗）在减小，当到达谐振频率fr[10]时呈现电阻性，继续增加频率则呈现感抗特性，此时电容也失去“本性”，这是高频电容不能接受的。谐振频率取决于ESL 的大小，当ESL 很小时，谐振频率很高，也就是ESL 决定着电容器的工作频率上限。

图1 高频电容阻抗模型Fig.1 High frequency capacitance impedance model

式中：Z为等效阻抗；ESR 为等效串联电阻；f为工作频率；C为电容器电容量；fr为谐振频率。

电容器的ESL 是客观存在的，无法被消除，只能通过合理的设计尽可能降低。

2 低ESL分析

2.1 极板引出形式

薄膜电容器早期采用有感式[11-12]引出方式见图2，即引线从金属极板某处单点或单线引出，电流在极板上沿薄膜横向逐圈旋入，极板变成薄片状线圈，此结构电容ESL 较大，在低频时都是不建议使用的。随着制造工艺的发展，火焰喷涂或电弧喷涂锌丝或锌锡合金丝，细小金属颗粒附着在心子的上下端面如图3 所示，形成薄片喷金层，再通过引线将电极引出，这样的引线结构为电流提供纵向通道流向喷金层，解决了电流逐圈旋入带来的寄生电感，因此端面喷金引出的电容叫作无感电容。

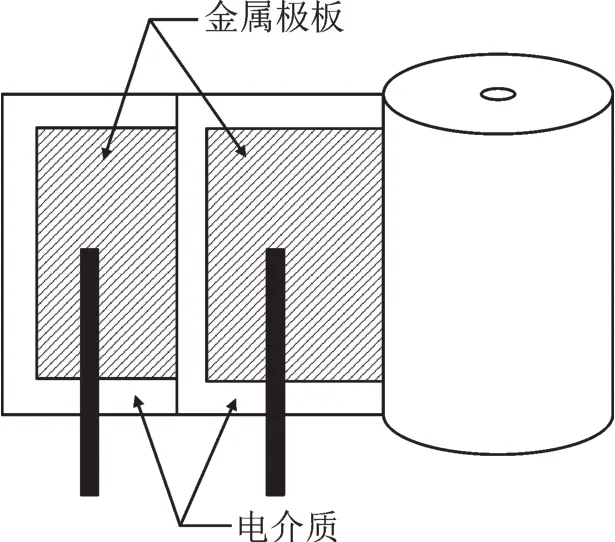
图2 有感电容内部结构Fig.2 Internal structure of inductive capacitor

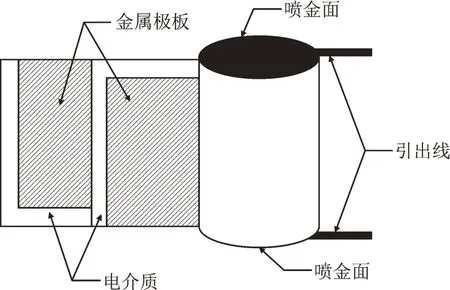
图3 无感电容内部结构Fig.3 Internal structure of non-inductive capacitor

2.2 引线寄生电感

电容器心子从喷金面引出电流的引线通常采用镀锡铜线或镀锡铜包钢线（CP 线），高频电流通过引线时由于集肤效应会增加电容器的等效串联电阻[13-15]，同时因为寄生电感的存在，感抗随着频率的增加而增加。

对于一根长为l、半径为r的直引线，其寄生电感记为L，通过引线的高频交流电流记为i，不考虑集肤效应，认为电流沿引线横截面均匀分布，引线横截面见图4，根据磁场安培环路定理[16]可计算距离引线轴线x处磁场强度Hx（A·m-1）公式为

图4 引线截面微元电流示意图Fig.4 Schematic diagram of tiny element current in lead section

在距离引线轴线x处的磁感强度Bx公式推导如下

式中：μ0为真空磁导率，4π×10-7N·A-2；μr为相对磁导率。

在距离引线轴线x处取微元面积ldx 见图5。

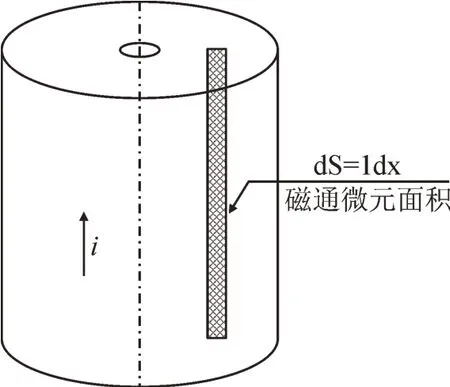
图5 磁通微元面积示意图Fig.5 Schematic diagram of the area of the flux micro element

对磁通量积分后求得引线内侧寄生电感L公式为

当x大于引线半径r时，距离引线轴线x处磁感强度Bx公式为

距离轴线大于le0.446r/l处的磁感强度较小[17]，忽略距离大于l·e0.446r/l处的磁通，引线外侧寄生电感计算公式为

引线总寄生电感公式为

考虑集肤效应时，电流密度在引线表面处随频率增大而增大，在轴心处随频率增大而减小。引入电流透入深度Δ[17]：从引线表面起，电流密度逐渐减小到表面电流密度e-1的深度。

式中：Δ 为电流透入深度，cm；ρ为引线电阻率，Ω·cm；f为电流频率，Hz。

简化引线导体表面到电流透入深度Δ 的电流分布（线性），忽略引线轴心处的电流（高频集肤效应明显），集肤效应下引线内侧寄生电感公式为

集肤效应下（电流透入深度Δ）引线总寄生电感公式为

可以得出结论：引线寄生电感随引线长度增加而增加，随引线半径增加而减小，集肤效应不改变物理结构参数对寄生电感变化趋势，简化模型忽略集肤效应采用式（10）进行后续分析。

2.3 心子寄生电感

对于无感卷绕电容器心子，通过电流时金属极板可以等效成电流柱薄壁层，薄壁层中间充满电介质，电荷受到洛伦兹力无法向心子表面聚集，即心子看成长导体时由于电介质的束缚无集肤效应。根据2.2 节不考虑集肤效应引线电感计算结果推理，心子电感计算公式为

式中：H为心子高度（喷金面到喷金面之间跨距）；R为心子半径。

从式（14）可看出，选择窄膜设计，降低心子高度H，同时增大心子半径R，这样“矮胖”型电容器心子可以降低心子寄生电感。

将卷绕型圆柱心子进行压扁，制成横截面为矩形电容器心子，矩形心子横截面上长度记为a，宽度记为b，压扁后的心子半径长度R用长宽和的一半（a/2+b/2）进行替换，可以得到压扁成矩形的无感式卷绕心子电感计算公式为

2.4 引线心子互感

磁场强度在空间具有方向性[18-22]，电容器ESL并不是引线和心子电感的简单代数相加，还要考虑引线与心子之间的互感。

径向引线的电容器心子电流磁场示意图见图6所示，引线电流i1至心子电流i2至引线电流i3在空间形成的磁感强度（右手螺旋定则，垂直纸面向里）是相互叠加的，存在互感作用。

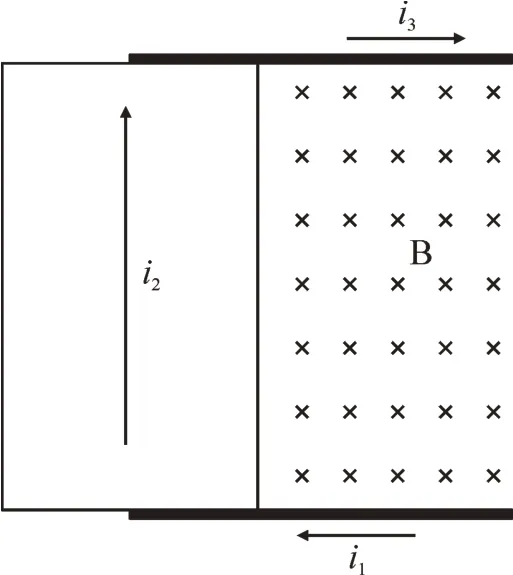
图6 径向引线电流磁场示意图Fig.6 Schematic diagram of radial lead current magnetic field

研究引线和心子包围空间区域的磁场，引线电流i1上的自感生电势e11公式为

式中，L11为电流i1的自感。

心子电流i2在空间形成的磁场叠加在i1上的互感生电势e12公式为

式中，L12为电流i2对电流i1的互感。

引线电流i3在空间形成的磁场叠加在i1上的互感生电势e13公式为

式中，L13为电流i3对电流i1的互感。

引线i1上的感生电势e1公式为

同理可求心子电流i2和引线电流i3的感生电势e2和e3，电容器总感生电势的计算如式（20），可以判断Lij>0(i≠j)，径向引出引线互感的存在增加整个电容器的ESL。

式中：e1、e2、e3电流i1、i2、i3的感生电势；Lij>0(i≠j)为电流j对电流i的附加感生电势作用系数（互感）；L11、L22、L33自感。

轴向引线的电容器元电流磁场示意图见图7，取电流微元Idl，对空间A 点的磁感强度dB由毕奥-萨伐尔定律计算，见式（21），磁感强度数值与矢径模平方成反比，轴向引出引线相比径向引出引线极大程度上削弱引线与心子之间的互感作用，引线和引线之间的互感影响由于矢径模较大可以忽略不计。

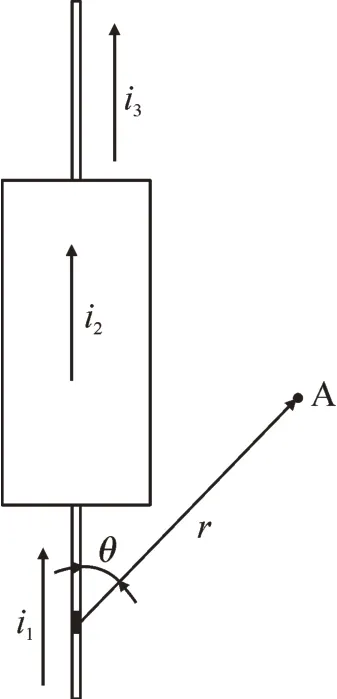
图7 轴向引线元电流磁场示意图Fig.7 Schematic diagram of axial lead element current magnetic field

式中，L12、L21、L23、L32数值上小于式（20）相应数值，L13和L31因为轴向引出矢径模平方（见式21）较大导致引线之间互感可以忽略不计（L13、L31代入0）。电容器ESL 由心子和引线之间自感和互感组成，轴向引出时互感数值小于径向引出，所以电容器引线轴向引出可以有效降低ESL。

2.5 实验数据分析

本文实验设备采用TH2826 数字电桥LCR 测试仪，径向引出成品电容若干，在常温常湿标准大气压下进行测量，每3 个同品类电容测试自感后取平均值，计算自感量时取引线电感和心子电感代数和，实验测试数据和计算数据记录见表1。

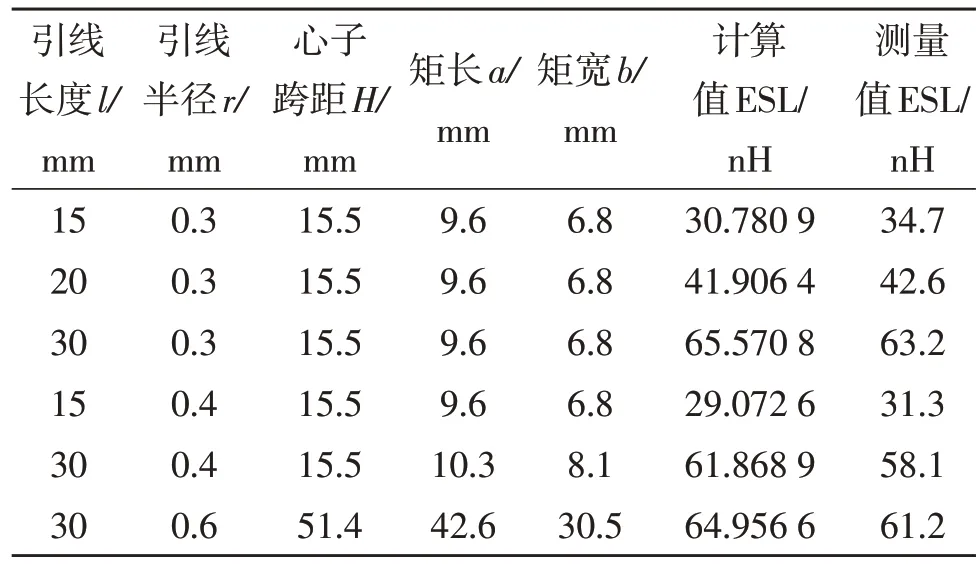
表1 ESL计算与测量Table 1 Calculation and measurement of ESL

在测量误差允许范围内和ESL 估算许可条件下，从表1 分析可知，引线长度对于电容自感组成占有相当大比重，减小引线长度是降低电容ESL 的有效方式；对于压扁型塑壳封装或粉末包封的电容器，（a+b）/H 取值一般在0～2（实际心子外形和塑壳尺寸限制）之间，可当有界变量处理，其ESL 取决于跨距H，短跨距是降低电容ESL 的合理方向。

3 结语

1）本文对于磁场、导体、电流密度等计算时采取适当、合理的简化与等效，不能定量地准确计算出ESL 数值，但是能定性判断降低ESL 方法。

2）对于引线部分，在设计电容器时减小引出线长度，采用扁引出线且增大引出线长度与宽度的比值（扁铜片），在设计条件允许的情况下可以采取增大引线直径（螺母引出电极）等方式降低ESL。

3）对于心子部分，在设计电容器时，选择金属极板的宽度时尽可能越小越好，降低喷金面之间的距离且增大心子半径，“矮胖”型心子设计能有效降低ESL。

4）相比于引线（镀锡铜线或CP 线）径向引出，轴向引出引线可降低互感影响，能降低电容器的ESL。