BP神经网络在供水管网余氯变化中的研究①

赵加斌

(上海市政工程设计研究总院(集团)有限公司,上海 200092)

1 背景概况

余氯是反映供水管网水质的重要指标,是保障高品质饮用水微生物安全与口感要求的重要依据。余氯的衰减反应机理复杂,且影响因素众多,现实中供水管网往往受监测点数量和监测指标的限制,难以满足机理性模型的构建要求。随着社会经济的发展与供水设施的建设投入,供水的主要矛盾已经从水量矛盾开始向水质矛盾进行转变,人们对于高品质饮用水的需求越来越高。然而饮用水的品质并不是取决于单一因素,从源水到用户龙头每个环节的严格把控,都是对高品质饮用水的保障。其中,水厂净化处理之后得到的高品质水,大多是由供水管网传输到每位用户,但是系统庞大的供水管网结构复杂,运行工况时刻变化,供水水质在管网中的变化也具有缓慢性、潜在性与突变性等特点。供水管网的水质安全和高品质输配至关重要。

管网中余氯的衰减速率与水中的有机物、无机物、溶解氧、流速、温度、水龄、初始氯浓度、微生物和管道腐蚀程度等因素密切相关[1][2]。余氯的衰减反应机理复杂,且存在众多的影响因素。因此,余氯衰减的机理性模型往往都比较复杂,且所需的监测数据与监测指标也比较多,在实际中的应用往往受到很大限制。随着数学理论的相关研究不断发展,与之相关的非机理性的管网余氯衰减模型也愈发受到关注。其中:由于神经网络模型不涉及深层次的反应原理,所需要的数据只需要有效,充分,有代表性即可。其主要通过对数据资料的机器学习训练得到在数据中的变化规律,从而被广泛应用于管网水质模型的研究中[3]。因此,采用BP神经网络来建立供水管网的余氯衰减模型,主要是研究余氯在管网中的变化规律,为高品质供水的管网安全输送与水质保障建立研究基础。

2 BP神经网络

神经网络是将大量的人工神经元广泛的连结而成,用以模仿人脑的神经网络的复杂系统。

BP (Back-Propagation)神经网络,是反向传递误差的神经网络,其通过隐含层向输入层逐一传递误差,并且将误差分给各个单元,得到的误差信号作为修正各个单元权值的依据。通过不断的修正权值,可以逐步逼近到最终可以满足精度要求的BP神经网络模型[4]。

具体结构如图1所示。

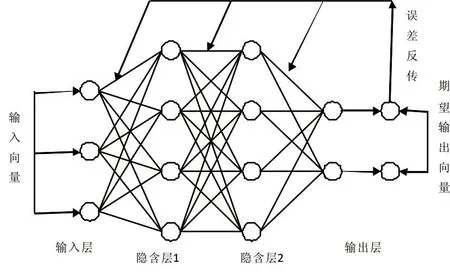
图1 BP神经网络模型结构

将BP神经网络用于供水管网水质模型,只要有足够的数据,就能充分利用神经网络强大的自学习能力来对供水管网水质的变化建模,并且模型具有较高的准确性。

3 实例分析

3.1 基本资料

以总面积为315平方公里,用水服务人口约31万人的南方某开发新区为研究对象,供水水源采用新区增压泵站增压上游清水来水后供给到新区。新区增压泵站采用氯胺消毒方式,现状供水管网管材主要为球磨铸铁管,管径主要分布在DN300～DN1200之间。根据新区供水系统的布局与各个区域的开发程度,选择在新区增压泵站出水点、南部居住与商业区管网末梢点与西部装备智造园区的企业末梢点布设水质监测点,具体如图2所示。

监测时间从2020年1月1日至2020年的11月20日,共监测数据样本324个,监测的水质指标主要为余氯值。通过余氯值的变化来了解当前供水管网的水质状况,并为余氯的投加与高品质水的输配提供依据。

3.2 BP神经网络余氯模型

本文以南方某开发新区供水管网的末端水质指标余氯作为建模对象,建立管网末端余氯这一水质指标的BP神经网络余氯模型。

设余氯指标的序列为D1(i),D2(i),…,Dn(i),其中n为余氯水质指标的数目。则预测指标的模型可以简单描述为公式(1):

Dn(t)=ψ(Dn(i))

(1)

式中:ψ(·)为非线性作用函数;

该模型就是要寻找最佳拟合理想结果的非线性作用函数ψ(·)。可以设置的神经元数量取决于网络中间层的神经元具有多少阶的导数。假使有任意阶导数的神经元,那么就可以有任意数量的中间层神经元。这样就使得3层的神经网络模型可以以理想精度(以实际工程需要精度为依据)逼近理想连续函数[5]。只要参数设置合理与得当,最终就可以得到一个较为准确的反应非线性关系ψ(·)。

由于本次研究中水质监测点的数量较少,且新区的主要用水区域位于南部的居住与商业区和西部的装备智造园区。因此,本文主要将2020年1月1日到11月20日的南部居住与商业区管网末梢点与西部装备智造园区的企业末梢点的余氯这个水质指标序列作为样本供BP神经网络建模。

考虑温度对于余氯的变化影响较为明显,且对于实际生产管理的运行控制也更为便利,因此,本文选择2020年1月1日到11月20日的每天平均温度替代时间这一参数来作为模型的影响因素更为合理。同时,新区增压泵站作为南部供水片区与西部供水片区的源头,其出厂水的余氯浓度(初始氯浓度)对于管网末梢具有重要的影响。因此,本文将2020年的气温与新区增压泵站出厂水余氯浓度作为自变量,来模拟南部与西部管网末梢点的余氯变化情况。

由于该模型中的隐含层神经元采用Sigmoid型变换函数,而输出层采用线性变换函数,所以在对BP神经网络进行学习训练之前,要将水质样本进行归一化处理,从而使得各个要素严格落在[0,1]之间[5],并使用L-M算法用以确定该神经网络中的各个参数。

对于神经网络隐含层的节点数[6],则根据以下公式(2)确定:

Ny=(Ns+Nj)0.5+N

(2)

式中:Ny为隐含层的节点数;Ns为输入层的节点数;Nj为输出层的节点数;N为2～4之间的一个随机数;

将余氯监测样本数据分为检验集与训练集两个部分。其中:每个月的5号、10号、15号、20号、25号、30号的归一化的数据作为BP神经网络的检验集,2020年1月1日至11月20日的其他时间的实际监测值作为BP神经网络模型的训练集。

利用MATLAB的BP神经网络工具箱将该模型相关参数及数据进行调试。当隐含层节点数Ny=4时,模型收敛性最好。模型模拟结果与实测值之间的结果,如图3和图4所示。

从图3和图4中的模型训练阶段可知,用BP神经网络模型对余氯监测样本训练与拟合后,对于西部和南部供水管网末梢点的余氯模拟值与实际监测值均具有良好的拟合精度,相关系数均在0.80以上,均方根误差均在0.15以下。就该模型整体来看,用BP神经网络模型对新区供水管网末梢余氯指标建立余氯模型的拟合结果较为理想。

3.3 模型的检验与有效性评价

利用西部与南部管网末梢监测点的余氯样本(检验集),进行BP神经网络余氯模型的检验与有效性评价。模型预测结果与实际监测值之间的比较如图3至图4中的模型检验阶段所示。

总体上而言,BP神经网络模型对于西部与南部供水管网末梢点的余氯变化情况的预测值与实际监测值的变化趋势是相符的,相关系数均在0.85以上,均方根误差均在0.20以下。且在模型的检验阶段,可以明显从图中发现:能更好的吻合实际情况的模型是南部管网末梢点余氯变化模型。因此,为了更好检验BP神经网络的模型预测结果,再利用相对误差来进行模型有效性的分析评价,如表1所示。

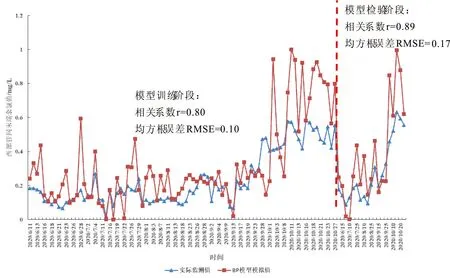
图3 对于西部管网末梢点,BP神经网络模型模拟值与实际监测值的比较

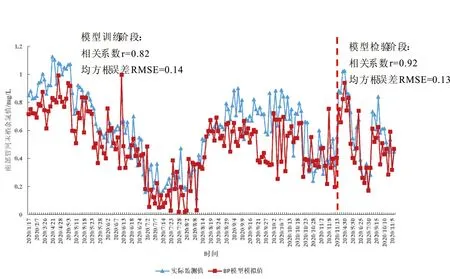
图4 对于南部管网末梢点,BP神经网络模型模拟值与实际监测值的比较

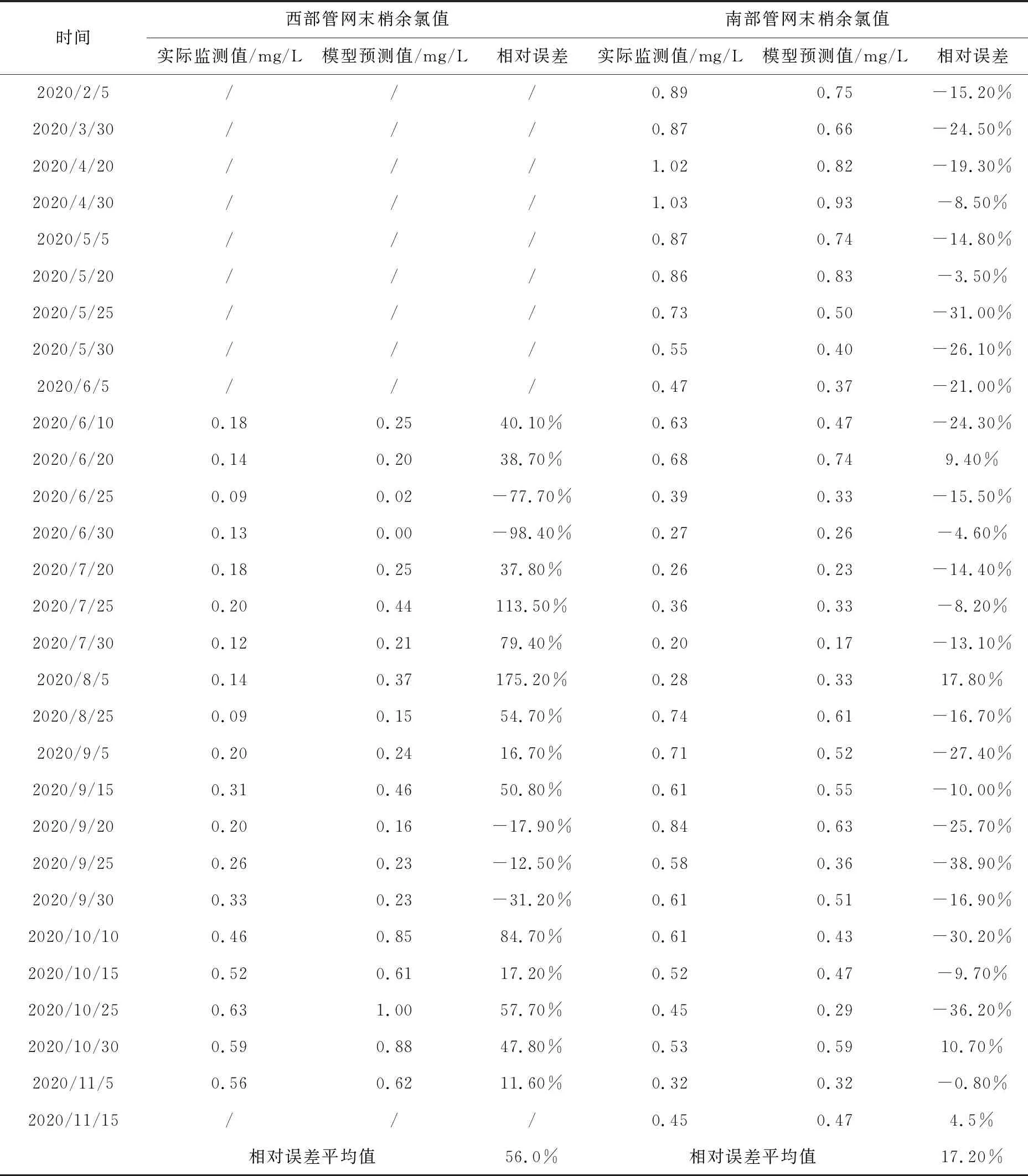
表1 BP神经网络模型相对误差的分析

利用相对误差,从模型有效性分析的结果来看,对于南部供水管网末梢余氯指标的BP神经网络模型检验更令人满意,相对误差可以控制在20%以内,约为17.2%。而对于西部供水管网末梢余氯指标的BP神经网络模型检验较为一般,主要可能与西部供水管网末梢的监测数据分布主要集中在6月至10月之间(2020年6月才安装在线余氯监测设备)、且数据样本相对南部监测点偏少有关。可见,BP神经网络模型作为一种特殊的非线性、高度复杂化的解决办法,对于基础数据量的大小依赖度较高。

4 结 论

本文以基础数据与机器学习为基础,利用有限的监测数据与监测指标,建立非机理性的BP神经网络余氯水质模型。通过对南方某开发新区的南部与西部供水管网末梢余氯变化的模拟研究,与实测值相比,均具有较好的模拟结果与拟合精度。同时可以发现:相比于西部供水管网,南部供水管网末梢余氯指标的BP神经网络模型效果更令人满意。可见,只要有一个有效、充分、有代表性的数据资料,BP神经网络模型就能较好的应用于供水管网的余氯水质变化研究。

该方法对于供水企业在降低监测数量与监测指标等条件的成本下,充分了解供水管网余氯衰减的变化规律,指导最佳出厂水余氯值,提高管网日常运行管理水平和高品质供水的安全保障具有重要的指导意义。