弹性特征约束下的矿物成分页岩脆性评价方法研究

曹丹平, 韩金鑫*, 肖竣夫, 刘强, 付飞琪, 刘迪

1 中国石油大学(华东)地球科学与技术学院, 青岛 266580 2 中国石油集团东方地球物理勘探有限责任公司物探技术研究中心, 河北涿州 072750

0 引言

随着社会经济的发展以及环境压力的不断提高,全国能源行业肩负着“碳达峰、碳中和”的任务,页岩气逐渐成为我国重要的低碳能源(刘合等,2021;田新等,2023).而页岩本身在自然状态下具有低孔低渗的特性,难以直接获得页岩油气资源,必须通过压裂的方式来形成复杂的裂缝网络,从而增加页岩地层的渗透能力来实现页岩储层的有效开发(贾长贵等,2012,刘喜武等,2022).其中,脆性是开展页岩可压裂性评价和压裂方案设计的重要指标,提高页岩储层的脆性评价精度对页岩油气开发具有重要意义.

常用的脆性评价方法主要包括弹性参数脆性评价方法和矿物组分脆性评价方法等.其中,弹性参数脆性评价方法主要利用杨氏模量和泊松比参数来计算脆性指数,通常杨氏模量高、泊松比低的岩石具有较高的脆性.基于矿物组分的脆性评价方法主要利用脆性矿物成分含量与总矿物含量的比值来计算脆性指数,石英等脆性矿物含量越高,岩石脆性越强,在页岩储层压裂时越容易形成复杂的裂缝网络.两种方法各有特点且相对独立,并均在实际应用中取得了很好的成效(Jin et al., 2014;Harbert et al.,2020).

采用页岩中矿物成分含量来评价页岩储层脆性时,其关键在于确定页岩储层中的脆性矿物成分及其含量,但岩石矿物组分多种多样,不同区域、不同储层类型往往发育不同的脆性矿物,在岩性比较简单的区域可以只考虑石英矿物的影响,而在复杂区域计算脆性矿物指数时则需要充分考虑石英、长石、方解石、白云石等更多矿物成分的影响(Zhang et al., 2017;张宜,2019).基于矿物含量的脆性评价方法在计算岩石脆性指数时,每种矿物往往都被赋予相同的权重系数,也就是将各矿物对脆性指数的影响等同对待.实际上,不同矿物的脆性是不一样的,对岩石整体脆性特征的影响程度也具有差异性(胡明毅等,2015;白佳佳,2022),在实际应用中应该充分考虑不同矿物成分对岩石整体脆性的差异性影响,从而有效提高岩石脆性计算结果的合理性及准确性.

如何标定不同脆性矿物对岩石脆性整体特征的定量影响程度是有效提高脆性评价精度的关键.不同脆性矿物成分的变化一定会改变岩石的弹性特征,导致杨氏模量、泊松比及其所反映的岩石力学性质发生改变.通过三轴压缩岩石物理实验有助于定量分析不同矿物成分对岩石整体脆性在贡献程度方面的差异性,并可以进一步采用矿物杨氏模量与泊松比的比值来表征不同矿物对岩石脆性特征的差异性影响.但不同矿物成分对岩石整体脆性特征的影响是一个复杂的非线性问题,传统的实验难以精确标定不同矿物及其含量对岩石脆性的定量影响关系.近年来,数字岩心技术在计算岩石弹性参数等方面发展迅速(Hou and Cao, 2022),通过对不同矿物组成的岩石图像进行数值模拟(Zhu et al.,2017;Das et al., 2019;Cao et al., 2022),能够直观反映不同矿物成分及其不同组合方式下的弹性特征(Haddad and Sepehrnoori,2016),通过弹性参数计算的脆性指数能够更加直接地反映出不同矿物组分对岩石脆性的影响,为定量评价不同脆性矿物成分对岩石脆性的影响提供了优越的实验条件,也为采用基于弹性参数的岩石脆性计算方法来定量标定不同的脆性矿物对岩石整体脆性的差异性影响程度提供了契机.

本文联合弹性参数和矿物组分两种脆性评价方法,通过开展数字岩石物理实验来定量刻画脆性矿物成分相对于黏土矿物对岩石整体脆性的贡献程度,在弹性特征的约束下求取不同矿物成分与脆性指数的定量关系及权重系数,提出基于矿物成分贡献程度自适应变化的脆性评价方法,避免了不同矿物平均化对岩石脆性指数计算的影响,更加准确合理地体现了不同矿物组分对页岩脆性的贡献.

1 基于数字岩石物理实验的脆性评价

1.1 数字岩石物理建模及实验原理

本文通过固体波动方程,模拟了岩石物理应力应变实验.固体运动由波动方程给出:

(1)

其中ρ为固体密度,u为位移场,S为压力场,F为体力项.

将每种矿物都假设为线性弹性的材料,利用胡克定律来模拟固体矿物的本构关系:

σij=λδijεαα+2μεij,

(2)

式中λ和μ是拉梅常数;δij和εij分别是应力张量和应变张量的元素.

在页岩顶部施加垂直于岩石顶部和平行于岩石顶部的正弦位移:

u=A*sin(2πtf),

(3)

其中u是岩石顶部的位移;f是正弦位移的频率;t是正弦位移的时间,A为振幅,大小为10-9m.

为了讨论矿物成分对岩石脆性的定量影响关系,本文构建了一个页岩数字岩石物理模型,模型大小为5 mm×5 mm,来模拟微观下页岩岩心的实际状态(Wu et al., 2020),采用有限元方法对模型进行网格剖分,以满足模型求解时的稳定性.为了更好地模拟实际页岩岩心中矿物的分布情况,在数字模型中矿物随机分布,不同的颜色代表不同的矿物,包含石英、黏土、有机质、长石、方解石、白云石、黄铁矿七种矿物.模型边界条件设置是数字岩石物理实验在模拟纵横波传播时效果好坏的关键,为满足模型的稳定性,更加符合数字岩石物理实验的条件,本文在模拟纵波传播时,岩石两侧的边界固体位移在X方向上为0(Quintal et al., 2016),使得应变只能发生在纵向方向;在模拟横波传播时,岩石两侧的边界为周期性边界条件(朱伟等,2020),在模拟纵横波传播时,底部边界固体的位移皆为0(图1).

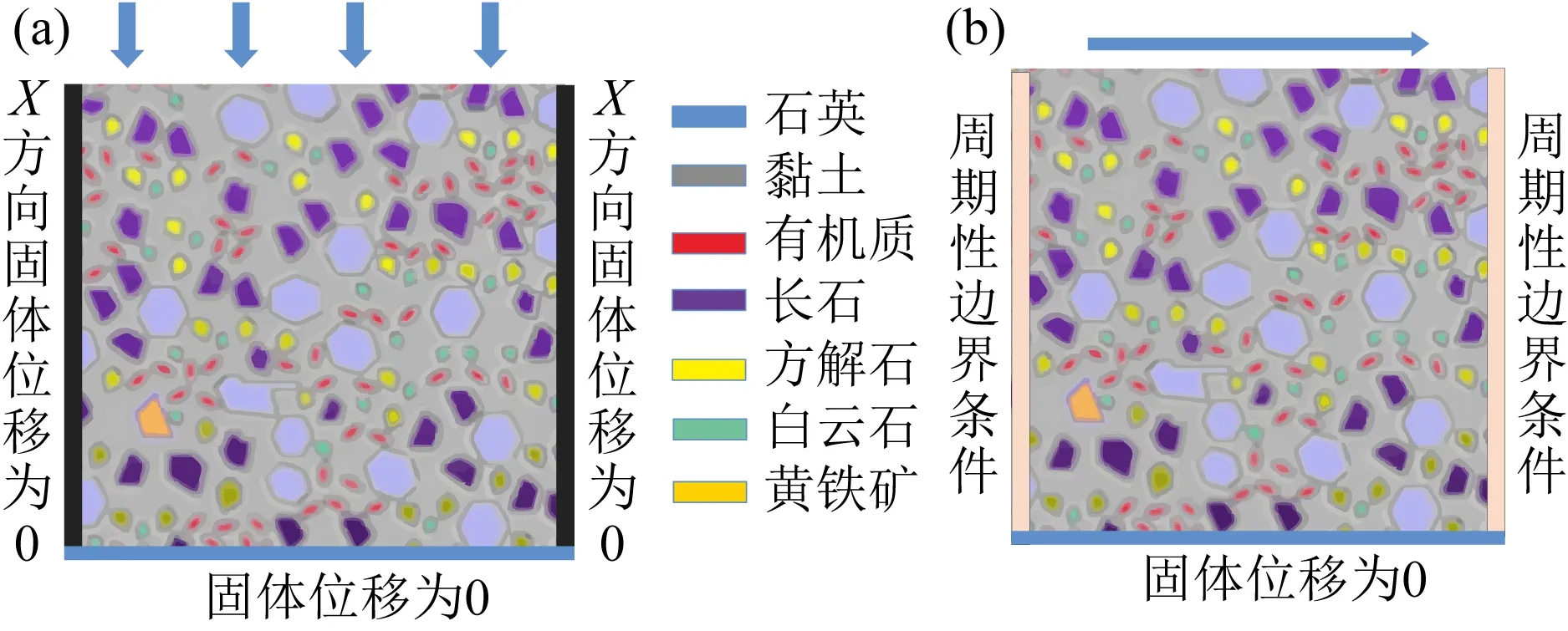
图1 页岩数字岩石物理模型及数值模拟边界条件设置 (a) 纵波传播时边界条件; (b) 横波传播时边界条件.Fig.1 Digital petrophysical model of shale and setting of boundary conditions for numerical simulation(a) Boundary conditions of longitudinal wave propagation; (b) Boundary conditions of shear wave propagation.

在模拟纵波传播求取纵波速度时,在岩石顶部施加一个垂直于岩石顶部的正弦振动,X方向为水平方向,Y方向为竖直方向.计算Y方向的平均应力和平均应变,Y方向的平均应变是通过应变除以Y方向的岩石长度来计算的,有效P波模量Re(M)是由岩石顶部平均应力应变计算得到的,其计算模型为

(4)

(5)

其中,Re(M)表示有效P波模量;σP表示峰值处应力振幅;εP表示峰值处的应变振幅;t0表示峰值处的时间;VP为纵波速度;ρ为矿物的密度,f为100 Hz.

在求取横波速度时,在岩石顶部施加一个平行于岩石顶部的正弦振动,计算X方向的平均应力和平均应变.剪切模量Re(G)计算方法与有效P波模量的计算方法类似,皆是由岩石顶部平均应力应变比计算得到的,其计算模型具体为

(6)

(7)

其中,Re(G)表示剪切模量;σS表示峰值处的应力振幅,εS表示峰值处的应变振幅;t1表示峰值处的时间;VS为横波速度,f为100 Hz.

因此,通过数字岩石物理实验可以直观地获得不同矿物组分条件下的纵横波速度等弹性参数,为基于弹性参数和矿物成分开展脆性评价及联合分析提供了桥梁.

1.2 基于数字岩石物理实验的弹性参数脆性评价方法

根据数字岩石物理实验获得的纵横波速度可以计算出动态杨氏模量、体积模量及泊松比(Fjær,2019),得到不同矿物组成下岩石的弹性参数,其计算模型为

(8)

(9)

(10)

其中Kdyn为动态体积模量;Edyn为动态杨氏模量;ν为泊松比.

利用Herbert等人利用的弹性参数脆性评价方法,对杨氏模量和泊松比做处理后计算得到岩石脆性指数B1,其计算模型为

(11)

(12)

(13)

其中υ为泊松比,E是杨氏模量,单位为MPSI.BRITE代表杨氏模量对脆性指数的影响;BRITυ代表泊松比对脆性指数的影响.杨氏模量的范围界定在1～8 MPSI,泊松比范围界定在0.15～0.45之间,当E=8 MPSI且υ=0.15时,认为页岩将“100%”易碎,可压裂性好;当E=1 MPSI,υ=0.45时,岩石被视为“0%”脆性的岩石,其可压裂性差.

本文也采用了Guo等(2013)利用的弹性参数脆性评价方法B2,利用杨氏模量与泊松比的比值来计算脆性大小:

(14)

(15)

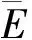
1.3 基于矿物成分的脆性评价方法

基于矿物成分的脆性指数评价是对页岩储层开展脆性评价的重要方法(黄锐等,2014;Ye et al., 2020),它们的共同特点是将脆性矿物与总矿物含量的比值作为岩石脆性指数,但在具体呈现方式上具有差异性.可以将石英、长石、方解石、白云石等多种脆性矿物的共同影响全部列出,如公式(16)所示(陈吉和肖贤明,2013);也可以将石英与碳酸盐矿物的影响合并在一起考虑来作为对岩石脆性的影响,如公式(17)所示(李钜源,2013);也可以仅考虑石英矿物的影响,如公式(18)所示(才博等,2012);还可以进一步考虑杨氏模量与泊松比在矿物脆性评价中对岩石脆性的影响,如公式(19)所示(刁海燕,2013).公式(16)—(19)为

(16)

(17)

(18)

B6=

(19)

其中B3、B4、B5、B6代表各种脆性指数计算方法;W代表矿物在总矿物含量中所占比重;YM代表矿物的杨氏模量;PR代表矿物的泊松比.矿物脆性评价方法B3、B4将每种矿物对岩石脆性的贡献视为等同的,例如B3将白云石、方解石、长石、石英矿物对岩石脆性的影响视为等同,而实际上,由于每种矿物的化学成分不同,其弹性特征也会存在差异,对岩石脆性的贡献也会存在很大差异.B6将矿物杨氏模量与泊松比的比值作为约束进行岩石的脆性评价,但B6与B3都只将石英矿物作为脆性矿物来开展岩石的脆性评价.

1.4 基于数字岩石物理的弹性参数和矿物组分脆性评价方法联合实验流程

弹性参数脆性评价方法与矿物脆性评价方法都具有其特点且相对独立,弹性参数脆性评价方法能够从岩石的弹性特征上计算岩石整体的脆性特征,矿物脆性评价方法可以通过岩石的矿物组成对其进行脆性评价,因此本文综合考虑两种方法的优势,设计了基于数字岩石物理的弹性参数和矿物组分脆性评价方法联合实验流程(图2),构建基于矿物成分贡献程度自适应变化的脆性评价方法.

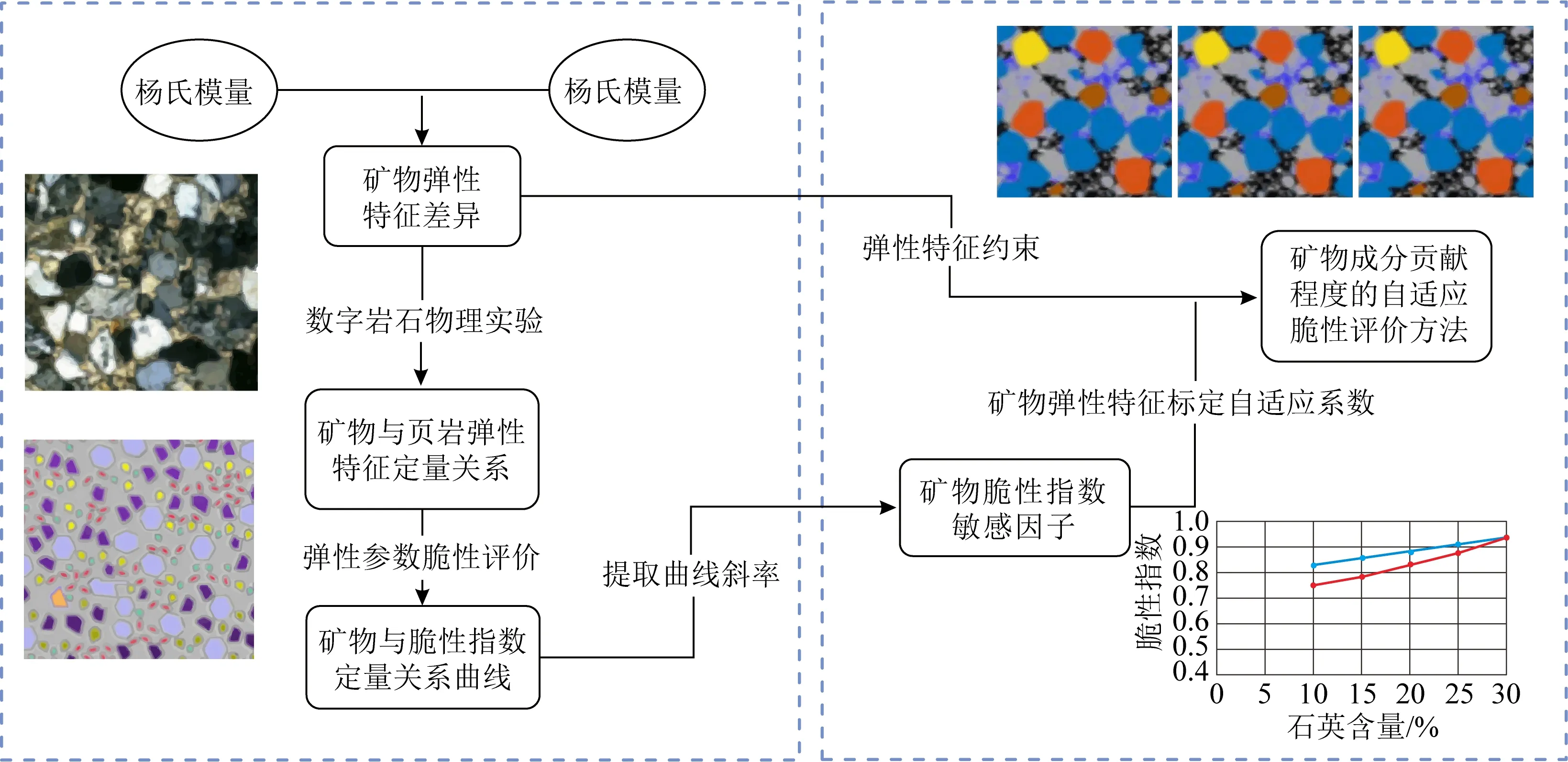
图2 数字岩石物理实验流程图Fig.2 Flow chart of digital rock physics experiment

首先,提取不同矿物成分的杨氏模量与泊松比,明确矿物弹性特征的差异性;其次,在设计数字岩石物理实验时,利用杨氏模量、泊松比及密度来表征不同矿物成分的弹性性质,通过控制不同矿物成分含量的变化,研究纵横波速度随着矿物含量的变化规律,明确杨氏模量、泊松比与矿物成分间的关系,从矿物的弹性特征上综合分析不同矿物对页岩脆性的影响,进而明确不同矿物成分与脆性指数的定量关系;最后,通过提取不同矿物成分与脆性指数关系曲线的斜率,作为矿物脆性指数敏感因子(矿物弹性特征标定的自适应系数),根据该联合实验流程提出矿物成分贡献程度自适应变化的脆性评价方法:

(20)

其中B7为构建的基于矿物组分贡献程度自适应变化的矿物脆性评价方法;i为矿物种类;Wi为地层中矿物的体积百分含量;W总矿物为地层中矿物总含量;Ai为矿物弹性特征标定的自适应系数.不同矿物组分的弹性特征不同,对岩石脆性的影响程度也不同,因此需要针对不同的矿物成分的差异来构建脆性评价方法,本文开展数字岩石物理的目的就是精确标定不同矿物成分的系数,从而在脆性评价中体现出不同脆性矿物的贡献程度的差异.

2 数字岩石物理实验分析

2.1 模型的矿物成分组成及参数设计

采用岩石物理手册等资料(Carmichael,1984)中石英、黄铁矿、方解石、白云石、长石、黏土的杨氏模量、泊松比及密度信息(表1),以此来表征不同的矿物.岩石中矿物组成及其矿物弹性特征的差异都会引起岩石整体弹性特征的变化,从而造成岩石整体脆性发生改变.在本次数字岩石物理实验中,设定了模型中矿物组成的初始值,其中黏土含量40%、长石含量15%,方解石含量10%,石英含量20%、黄铁矿含量3%,白云石含量10%和有机质含量2%(图3),其中黏土矿物、石英、碳酸岩含量较多,而黄铁矿与有机质含量较少.

表1 不同矿物弹性及密度参数Table 1 Elasticity and density parameters of different mineral

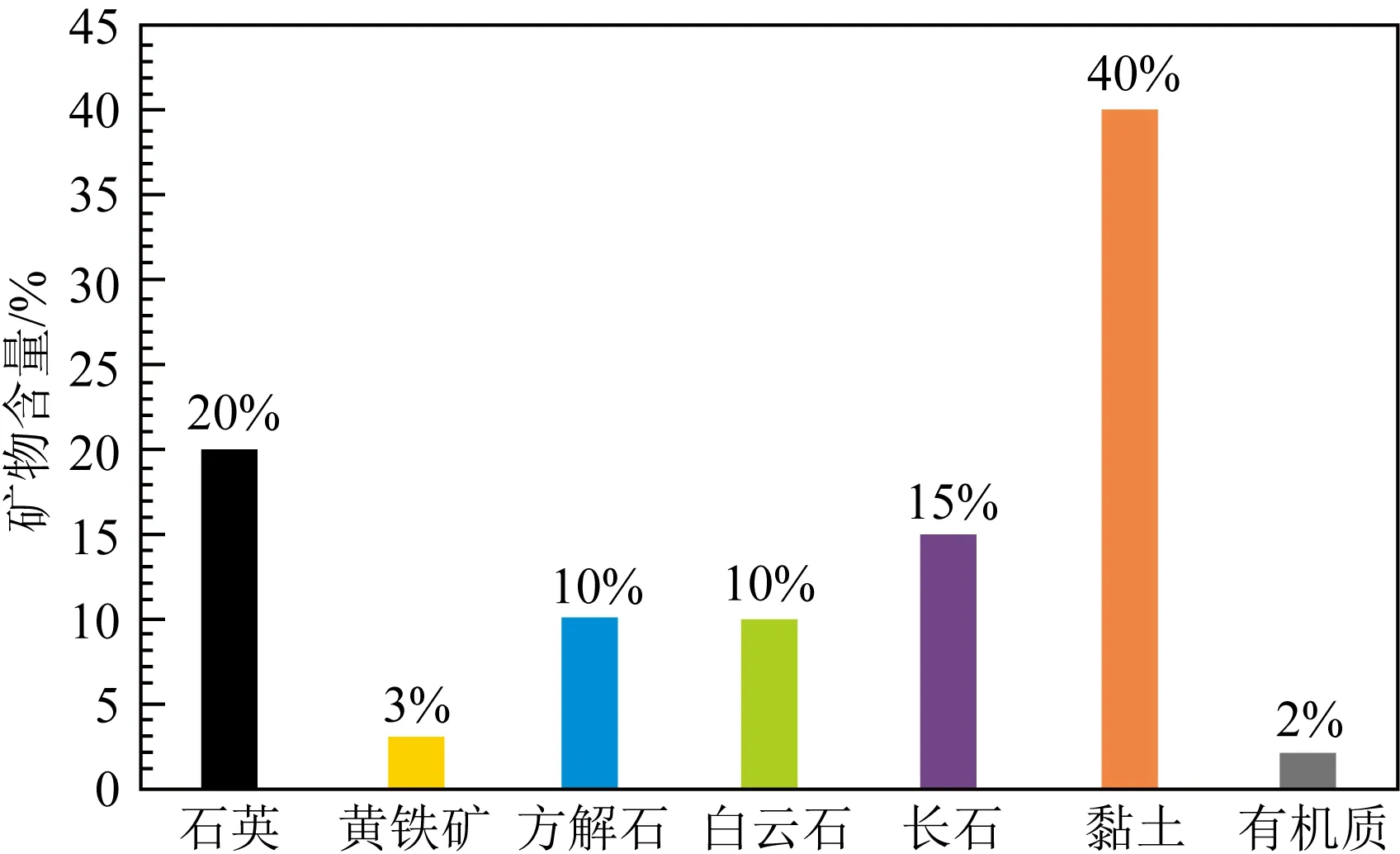
图3 模型中矿物组成的初始值Fig.3 Initial values of mineral composition in the model

同时也设定了矿物在页岩模型中的合理变化范围(图4),由于不同工区对脆性矿物的定义不同,而黏土矿物作为典型的塑性矿物是普遍认可的,可以作为标尺来衡量其他矿物相对于黏土对脆性的贡献情况.因此本文将黏土矿物对岩石脆性的贡献假设为0,在控制矿物含量变化时,黏土和其他矿物之间存在矿物替代.即在模型的初始条件下增加或减少其中的一种矿物成分含量,相对应的,黏土含量减少或增加对应的含量,其他矿物含量保持不变,以此来控制矿物含量的变化,研究不同矿物成分相对于黏土矿物对岩石脆性的相对影响.

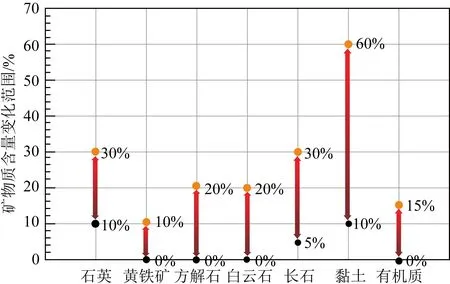
图4 不同矿物含量变化范围Fig.4 Variation range of different mineral contents

2.2 矿物成分对弹性参数的定量影响关系

页岩储层中矿物组成不同,其弹性特征也会存在明显的差异.图5是不同矿物成分组成的数字岩石模型,根据公式(9)—(10),可以计算出不同矿物成分与动态杨氏模量和泊松比的关系(图5),得到了不同矿物成分与模型的纵横波速度、动态杨氏模量及泊松比的定量影响关系.随着石英、黄铁矿、方解石、白云石、长石矿物含量的增加,模型的纵横波速度也在不断增加;而有机质含量越高,纵横波速度越小.其中泊松比反映了岩石的抗破坏能力,杨氏模量反映了岩石在压裂后保持裂缝稳定的能力(Rickman et al., 2008),两者综合反映了岩石的力学性质,杨氏模量越大,泊松比越小,岩石的脆性特征越明显.随着石英、黄铁矿、白云石、长石矿物含量的增加,动态杨氏模量变大,泊松比减小,矿物与动态杨氏模量及泊松比关系曲线在图像上呈交叉形态,可以判定石英、黄铁矿、白云石、长石,相对于黏土矿物来说,对岩石脆性具有的积极的贡献;随着方解石的含量增加,杨氏模量变大,泊松比也随之增高,由于杨氏模量增加、泊松比减小是判断矿物是否为脆性矿物的标准,所以并不能从矿物与模型动态杨氏模量与泊松比的关系上去判断方解石、有机质对岩石脆性的贡献是积极的还是消极的,还需要进一步的讨论.

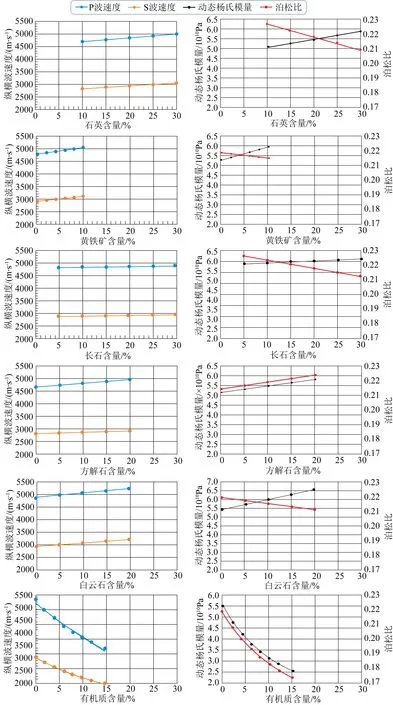
图5 不同矿物对弹性参数的定量影响关系Fig.5 Quantitative relationships between the effects of different minerals on elastic parameters

2.3 基于矿物成分贡献程度自适应变化的脆性评价方法

图5所得结论表明,仅仅通过杨氏模量和泊松比是无法准确地判断矿物对岩石脆性的贡献程度的,因此通过脆性评价方法B1、B2、B3、B4、B5、B6对不同矿物组成的页岩模型开展脆性评价,研究矿物在不同脆性指数评价方法下对岩石脆性影响的差异性,结果如图6所示.

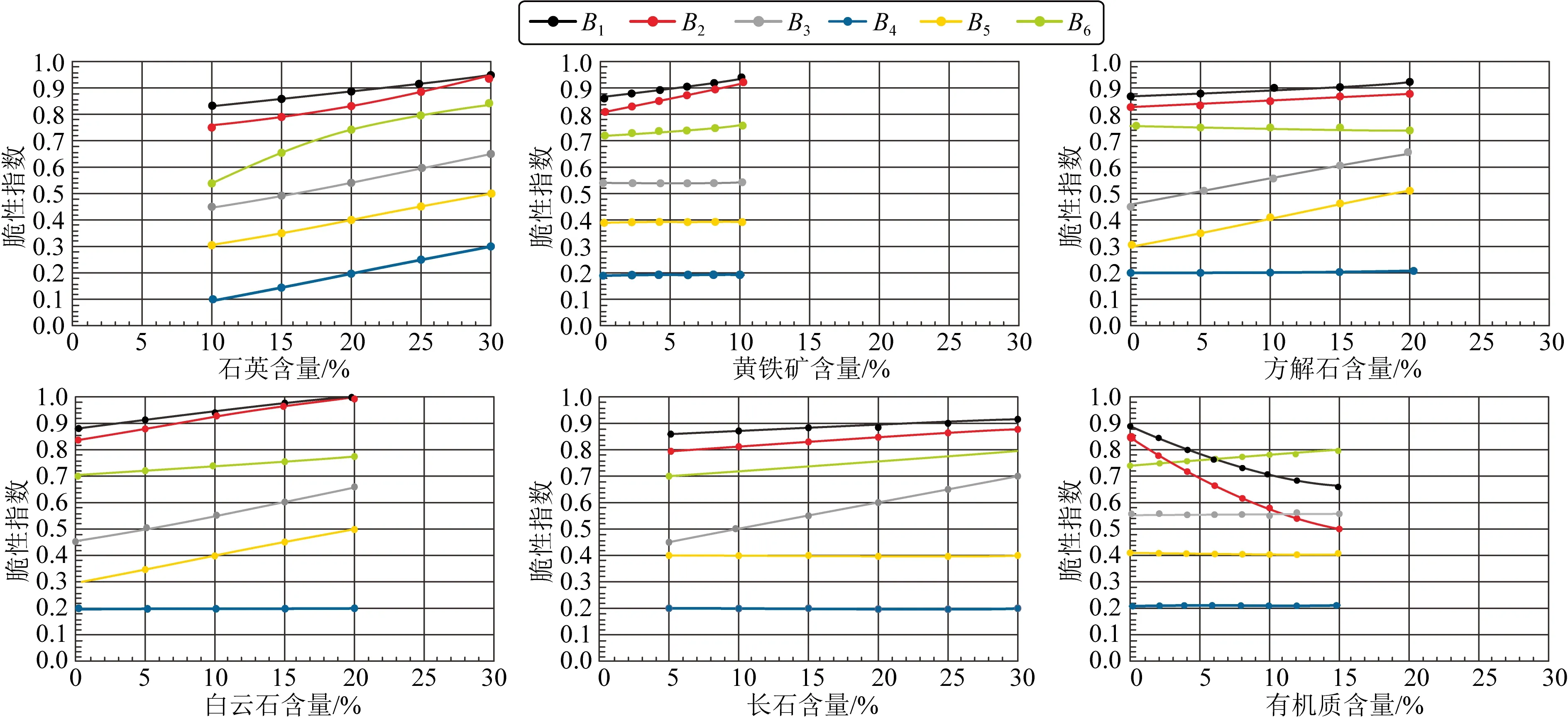
图6 不同矿物成分对页岩脆性指数的影响关系Fig.6 Relationship between different mineral compositions and shale brittleness index

可以发现随着矿物含量的增加,不同的脆性评价方法在相同的矿物组成下存在很大的差异,其中脆性指数数值大小与变化趋势发生比较明显的变化.对比矿物脆性评价方法B3、B4、B5、B6的结果,B6的脆性指数的数值明显大于B3、B4、B5所得的脆性指数,与B3、B4、B5方法所得结果作比较,B6所得结果中方解石对矿物脆性指数的影响得到了相反的趋势.B5、B6仅把单一矿物作为脆性矿物进行脆性指数分析,B3、B4则把不同脆性矿物对页岩脆性指数的影响平均化,导致脆性评价结果难以体现不同矿物成分的差异.结果表明,矿物成分的差异对脆性指数的数值影响很大,需要针对脆性矿物的差异来体现不同矿物成分对脆性的作用程度.

弹性参数脆性评价方法B1、B2所得结果与矿物脆性评价方法B3、B4、B5、B6所得结果进行比较,可以发现,随着石英、黄铁矿、白云石、方解石、长石矿物含量的增加,弹性参数脆性评价结果数值上大于矿物脆性评价的结果,且矿物含量的增加对两种弹性参数脆性评价方法B1、B2所得结果的影响趋势是一致的,其中石英、黄铁矿、白云石、方解石、长石都对岩石脆性有积极的响应;有机质含量的增加,则会使岩石的脆性减小,而B3、B4、B5、B6方法所得结果没有体现出有机质含量对页岩脆性指数的影响.

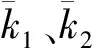
(21)

(22)

(23)

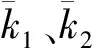
图7 矿物与弹性特征表征的脆性指数关系曲线斜率归一化结果Fig.7 The slope normalization result of the brittle index relationship curve characterized by minerals and elastic characteristics

(24)

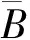
(25)

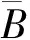
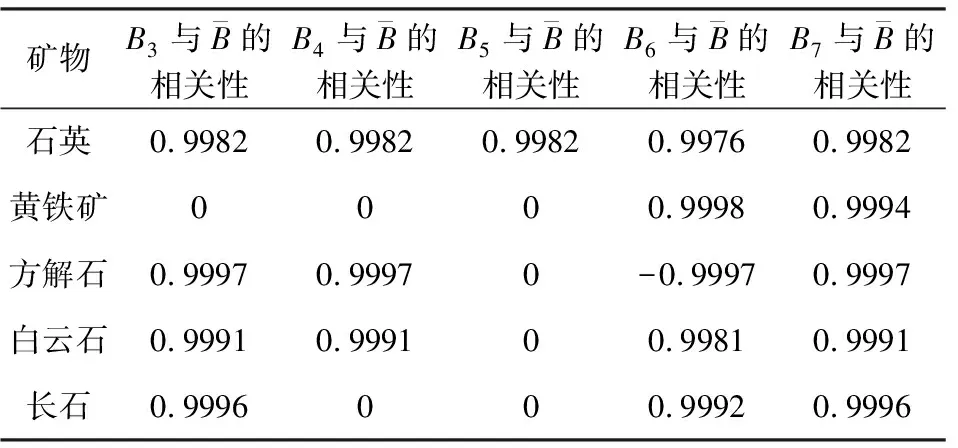
表2 矿物脆性评价结果与弹性参数脆性评价结果相关性Table 2 Correlation between mineral brittleness evaluation results and elastic parameter brittleness evaluation results

3 下寺湾地区的矿物脆性评价

本文以下寺湾地区的页岩数据为例开展脆性评价测试,该工区各矿物的体积分数如图8所示(秦晓艳等,2016),对其进行页岩脆性评价.其中,在15块页岩试样中,黏土矿物相对含量最高,范围在34.2%～68.6%之间,平均为51.4%;黄铁矿的相对含量最少,范围大致分布在0.4%～3.4%之间,平均为1.9%.长石的相对含量在14.4%～42.8%,平均为28.6%,石英的相对含量在7.8%～22.4%,平均为15.1%;碳酸盐矿物在总矿物含量的比重范围在0.9%～14.4%之间,平均为7.65%,将碳酸盐矿物划分为方解石和白云石,方解石和白云石在总矿物含量的所占比重皆为3.8%,我们取每种矿物含量的平均值来计算脆性指数.对其应用多种矿物脆性评价方法开展脆性评价,并与本文提出的矿物弹性特征约束下的脆性评价方法计算结果进行比较(图9).

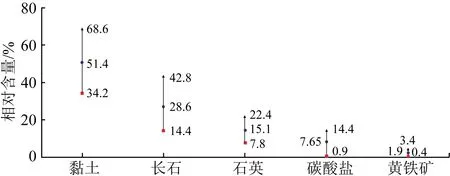
图8 下寺湾地区试样的矿物组成对比Fig.8 Comparison of mineral composition of samples in Xiasiwan area

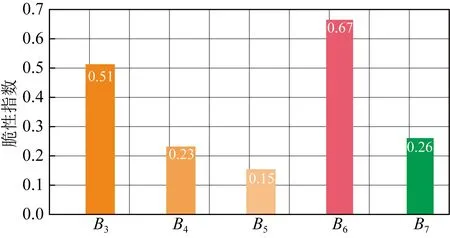
图9 下寺湾地区试样不同脆性评价结果对比Fig.9 Comparison of different brittleness evaluation results of specimens in the Xiasiwan area

结果表明,不同的脆性评价方法之间所得的脆性指数存在着很大的差异.利用B3进行页岩脆性指数评价时,虽然将长石、石英、碳酸盐作为脆性矿物,但是也忽略了黄铁矿的影响,同时该方法将每种矿物对岩石脆性的贡献视为等同的;利用B4进行页岩脆性评价时,该方法将碳酸盐和石英作为脆性矿物,同样将石英和碳酸盐对脆性指数的贡献视为等同,且忽略了长石与黄铁矿等矿物对脆性指数的影响;应用B5脆性评价方法开展脆性评价时,只将石英作为脆性矿物,而忽略了碳酸盐等矿物对页岩脆性指数的影响;而通过矿物脆性评价方法B6开展脆性评价时,虽然考虑了矿物弹性特征对脆性指数的影响,但仅把石英作为脆性矿物.而本文构建的B7是各矿物弹性特征约束下的矿物脆性评价方法,能够体现各矿物对岩石脆性贡献的差异性,能够更合理地反映不同脆性矿物对岩石整体脆性特征的影响程度,避免了平均化各矿物对脆性指数的影响,能够提高页岩脆性评价及可压裂性评价时的合理性.

4 结论和认识

页岩储层的脆性评价是勘探开发过程中重要的评价内容.本文在收集、调研前人研究成果的基础上,针对我国页岩储层矿物含量复杂以及矿物脆性评价方法存在局限性等问题,通过数字岩石物理实验,开展了矿物成分与页岩脆性关系的研究,联合弹性参数脆性评价方法,提出了根据矿物成分贡献程度自适应变化的页岩脆性矿物指数计算方法.本文主要取得以下认识:

(1) 刻画了矿物对页岩弹性特征影响的差异性.通过数字岩石物理实验的方式,得到了矿物含量变化与纵横波速度的关系,随着石英、黄铁矿、长石、方解石、白云石矿物含量的增加,页岩模型整体的纵横波速度也在不断增加.随着方解石含量增加,杨氏模量变大,泊松比也随之增高;而随着石英、黄铁矿、白云石、长石矿物含量的增加,杨氏模量变大,泊松比减小.

(2) 构建了根据矿物成分贡献程度自适应变化的页岩脆性矿物指数计算方法.通过数字岩石物理实验的方式,明确了不同矿物与脆性指数的定量关系,基于矿物成分贡献程度自适应的变化,构建了页岩脆性矿物指数计算方法,避免了将各矿物对脆性指数的影响平均化,准确地表征了不同矿物对岩石脆性贡献的差异性.将不同矿物脆性评价结果与弹性参数脆性评价结果进行相关性分析,发现该方法所得结果与弹性参数脆性评价方法所得结果间存在较好的相关性,从而验证了该方法的合理性.

(3) 以下寺湾地区试样的矿物组成为例,研究了不同脆性评价方法的差异性.结果表明,利用B3、B4对其进行脆性评价时,平均化了各矿物对脆性指数影响;B5只考虑了石英作为脆性矿物;B6虽然考虑了矿物弹性特征对脆性指数的影响,但仅把石英作为脆性矿物,忽略了长石、白云石、黄铁矿对脆性指数的影响.本文构建的B7是在基于不同矿物的弹性特征约束下的矿物组分脆性评价方法,综合考虑了矿物对脆性指数的贡献的差异性,能够更合理地反映不同脆性矿物对岩石整体脆性特征的影响程度,能够更精确地指导页岩可压裂性评价.