未来月球熔岩管科研工作站能源供给的数值模拟

周书红, 胡才博, 张怀, 石耀霖

中国科学院大学地球与行星科学学院, 中国科学院计算地球动力学重点实验室, 北京 100049

0 引言

熔岩管广泛分布在行星表面的火山区,是熔岩运输的最终结果(Zhao et al., 2017; Perkins, 2020).地球上的火山区也分布着大量的熔岩管,例如意大利的埃特纳火山(Calvari and Pinkerton, 1998)、夏威夷的基拉韦厄火山(Peterson et al., 1994)和澳大利亚的温达拉火山(Atkinson et al., 1975;Stephenson et al., 1998).熔岩管是在特定情形之下熔岩流动而形成的(Angelis et al., 2002; Haruyama et al., 2012;肖龙等,2018).熔岩管的形成通常包括以下几个阶段(Sakimoto et al., 1996, Angelis et al., 2002; Valerio et al., 2008; Perkins, 2020; 肖龙等,2018):火山喷发出来的低黏度熔岩流表面冷却并凝固形成具有一定厚度的外壳;外壳下的熔岩冷却速度较慢可以保持高温状态继续流动,从而在地表下形成熔岩通道;熔岩喷发停止后,熔岩可以从管道中流出,离开隧道形成熔岩管.

月球上也存在大量的熔岩管.月球表面存在很多蜿蜒的细沟,这些蜿蜒的细沟被认为是通过熔岩流和侵蚀过程形成的(Chappaz et al., 2014).科学家们认为月球上蜿蜒的细沟和熔岩管是相关的(Oberbeck et al., 1969; Greeley, 1971),提出了月海玄武岩上蜿蜒的细沟是熔岩管的设想(Greeley, 1971).2007年日本发射的月球极地轨道飞行器拍摄的图像中发现了月球上第一个直径65 m、深度数十米的熔岩管的天窗(Haruyama et al., 2009).随后几年,美国的月球勘测轨道飞行器(LRO)和圣杯号月球探测器(GRAIL)观测表明,月球表面下存在熔岩管,熔岩管的宽度可达几十到数千米(Robinson et al., 2010, 2012; Arya et al., 2011),延伸长度可达几百米到几百千米(肖龙等,2018).熔岩管的横截面通常呈拱形、圆形、椭圆形或锁孔形(Sauro et al., 2020; 肖龙等,2018).图1为地球上一熔岩管洞及理想情况下的熔岩管洞卡通示意图.

图1 熔岩管洞示意图 (a) 加那利群岛的熔岩管(图片引自https:∥www.universetoday.com/139021/); (b) 熔岩管洞卡通示意图.Fig.1 Schematic diagram of lava tube hole(a) Lava tube in the Canary Islands (Image from https:∥www.universetoday.com/139021/); (b) Cartoon diagram of the lava tube hole.

月球上的熔岩管一直被认为是在行星探索中建造人类基地的理想场所(Angelis et al., 2002;Haruyama et al., 2012; Zhao et al., 2017; Perkins, 2020; 肖龙等,2018;宋靖华等,2019).在熔岩管内建立科研工作站可以避免很多自然灾害,例如宇宙射线辐射、各类陨石及其喷出物的撞击(Chappaz et al., 2014; 肖龙等,2018).月球表面温度变化巨大,昼夜温差超过300 K(Haruyama et al., 2012; Prasad, 2020).月表较大的温差将阻碍未来在月球表面直接的有人和无人活动,而月球熔岩管内部的自然温度几乎恒定,因此是月球基地建设的最优候选区域(Angelis et al., 2002; Haruyama et al., 2012; Zhao et al., 2017; Perkins, 2020).作为月球科研站建设的理想场所,熔岩管还有其他好处:平坦的地板、密封的内壁、无尘的环境等等(Haruyama et al., 2012).

1 月球表面温度分布特征

由于月球没有大气层,月球表面温度在白昼和夜晚有较大的温差.关于月球表面温度的变化一直是科学家们关心的问题.在Apollo任务之前,月球表面温度的测量是基于月球微波波段热辐射的地球观测(Langseth and Keihm, 1977).20世纪Apollo载人登月计划为直接测量月球表面温度及热流变化提供了机会(Langseth et al., 1972; Keihm and Langseth, 1973; Langseth and Keihm, 1977).

Apollo任务期间进行了几次原位温度测量.Apollo 15号和Apollo 17号都成功地测量到月球表面和地下温度及其日变化和年变化.其中,Apollo 15号着陆点(26°N,3.6°E)的月表温度变化为从月昼最高温度374 K到日出前最低温度92 K(Heiken et al., 1991).Apollo 17号着陆点(20°N,30.6°E)温度变化为从月昼最高温度384±6 K到日出前温度102±1.5 K,一个完整的月球日周期(～29.5个地球日)内温度变化超过280 K,平均表面温度216±5 K(Keihm and Langseth, 1973; Heiken et al., 1991).Apollo 15和17着陆点温度测量结果表明,月表以下35 cm处的平均温度比月表分别高45 K和40 K,这是由于月球表面1～2 cm处具有极低的导热系数,而在～2 cm处的热导率是表面值的5～7倍(Langseth and Keihm 1977).由于月表极低的导热系数抑制了周期变化的月表温度的向下变化,在深度超过50 cm的月球近表区域的温度在～250 K保持恒定(Langseth et al., 1972; Langseth and Keihm,1977; Heiken et al., 1991).然而Apollo 15和Apollo 17的着陆点分别位于Hadley Rille和Taurus Littrow处,并不能代表整个月球表面温度变化的分布情况(Keihm and Langseth, 1973; Langseth and Keihm, 1977).2009年月球勘测轨道器(LRO)上的Diviner月球辐射计实验进一步测量了所有纬度、经度月球表面温度的日变化和季节变化(Paige et al., 2010).

Williams等(2017)根据Diviner月球辐射计实验获得的测量数据分析得出,月球表面最高温度出现在正午,最低温度在当地日出之前,其中赤道月表的平均温度为215.5 K,平均最高温度为392.3 K,平均最低温度为94.3 K,表明日温度变化为～300 K (Williams et al., 2017).极地地区的平均最高和最低温度分别为202 K和50 K,平均温度为104 K (Williams et al., 2017).南极地区的平均最高温度为大约比北极地区高11 K,但两极的平均最低温度基本相同(Williams et al., 2017).

月球表面大范围的严酷高温和低温以及巨大的温度波动将阻碍未来人类在月球上活动.月表具有极低的导热系数,对热流有抑制作用,因此在一定深度保持恒温(低温)的熔岩管内建立科研基地需要持续供热.除此之外,已有的研究还表明在极地地区可能的水冰分布与低于110 K的温度表现出强烈的空间一致性,水和其他挥发物可能存在于极地地区的冷阱中,这使得月球极地地区成为未来建立科研基地的绝佳候选者(Fisher et al., 2017; Li et al., 2018; Williams et al., 2019; Hoshino et al., 2020).因此我们建立了二维有限元瞬态热传导的数值模型,重点研究在赤道建立科研基地时熔岩管的供热及耗热量问题,并讨论了极地地区建站的情况,为未来在月球熔岩管内建立科研基地提供科学指导.

2 有限元模型

2.1 模型设置

我们分两个阶段来研究熔岩管的供热问题.将月球熔岩管从恶劣的自然状态改变到人类宜居状态是一个加热过程,称之为第一阶段.第一阶段完成之后,需要维持熔岩管的人类宜居温度,称之为第二阶段.从温度场的角度,第一阶段需要持续从熔岩管内部提供热流边界条件,第二阶段需要保持熔岩管内壁为恒温(人类宜居温度～293.15 K).为了计算熔岩管加热到宜居温度的时间(第一阶段)以及达到宜居温度后需要多少加热功率来维持热量(第二阶段),我们设计了两个模型分别研究这两个阶段的传热过程(图2).

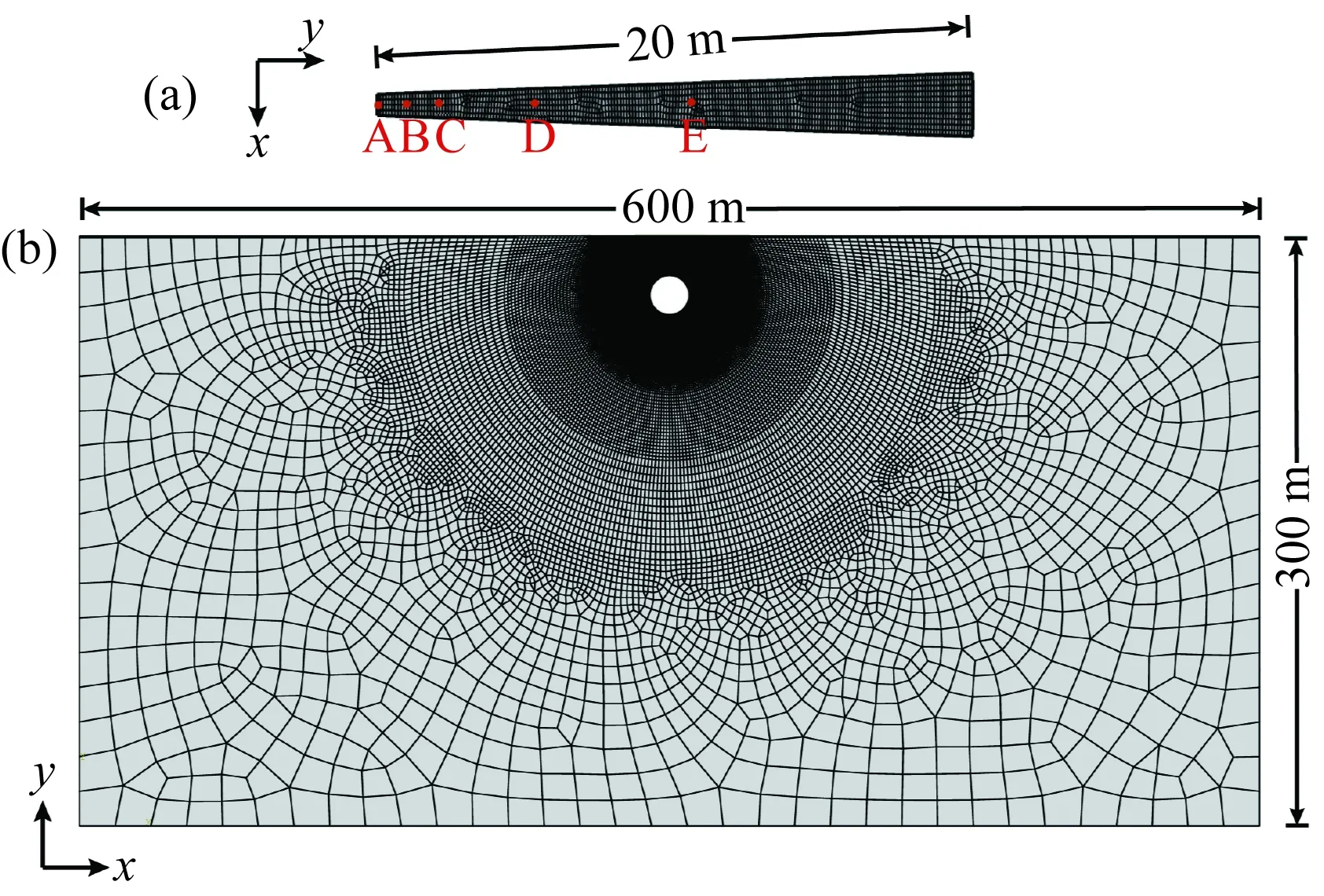
图2 有限元网格模型图(a) 第一阶段的网格模型:计算熔岩管加热到宜居温度需要多长时间; (b) 第二阶段的网格模型:计算熔岩管维持宜居温度需要多少加热功率.Fig.2 Finite element mesh model(a) The mesh model in the first stage: calculate how long it takes for the lava tube to be heated to a livable temperature; (b) The mesh model in the second stage: calculate how much heating power the lava tube needs to retain habitable temperature.

为了减少计算量,第一阶段的模型简化为熔岩管洞圆心角为4°的情况,其中熔岩管洞的直径为20 m,熔岩管洞的高度为20 m(图2a).第二阶段为了计算熔岩管洞维持宜居温度所需要的加热功率,我们设计了Model 0(图2b).由于月球表面的热性能为导热系数极低的风化层,其深层主要以导热系数较高的玄武岩为主(Lozano, 2016;Molaro et al., 2017),因此第二阶段模型的上表面均为1 m厚度的风化层,风化层以下为299 m深度的玄武岩层.熔岩管洞顶到模型上表面为20 m,洞直径为20 m,这与第一阶段熔岩管洞的大小一致(图2b).实际的横截面通常呈拱形、圆形、椭圆形或锁孔形(Sauro et al., 2020; 肖龙等,2018),本文将其简化为圆形的熔岩管横截面.

我们的模型都采用四边形网格.在第一阶段和第二阶段的模型中,为了保证模型计算结果的准确性,必须加密熔岩管壁附近区域的网格,较大的网格会造成传热较快从而导致计算结果不准确.因此我们对熔岩管壁附近的网格进行了加密,最小为0.1 m×0.1 m.其次,模型计算的时间步长必须取的很小否则影响热传导方程的迭代稳定性,因此第一阶段的模型计算总时间均为30天(地球日),时间步长为0.3 h.第二阶段的模型在前100年采用1个月的时间步长进行计算,在100年到1000年采用1年的时间步长进行计算.模型计算所采用的时间均为地球时.由于熔岩管的延伸长度可达几百米到几百千米(肖龙等,2018),如果采用三维模型将考虑熔岩管轴向方向的网格加密,造成三维有限元网格数量巨大,计算量过大,因此第二阶段模型简化为二维截面模型,二维截面参考图1的卡通示意图.

通过二维瞬态热传导的模型计算可以得到单位长度熔岩管的加热功率,而整个三维熔岩管的加热功率可以在二维模型计算结果的基础上乘以熔岩管的总长度得到.由于忽略了端部的三维散热效应,我们的模型计算结果仅可以提供最低能源供应的量级的估计.

2.2 控制方程

本研究使用有限元分析软件Abaqus进行模型试验(Abaqus, 2016).

首先我们求解了瞬态热传导方程:

(1)

式中,ρ为岩石密度、cp为定压比热,T为温度,t为时间,k为热传导系数.由于岩石的放射性生热率很小,因此模型的计算中不考虑热源的影响.

在模型中我们还计算了热流密度q:

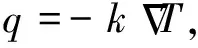
(2)

其中第一阶段的模型(图2a)使用了表1中玄武岩的参数进行计算熔岩管加热到宜居温度需要多长时间.第二阶段的模型(图2b)使用表1中的材料参数计算熔岩管维持宜居温度的热功率.

表1 有限元模型的材料参数Table 1 Material parameters of finite element models

2.3 初始条件及边界条件

Apollo 15和Apollo 17测量得出在深度超过50 cm的区域的温度在～250 K时保持恒定(Langseth et al., 1972; Langseth and Keihm, 1977; Heiken et al., 1991).因此对于第一阶段的模型(图2a),我们给定整个模型的初始温度为250 K.底边界为熔岩管壁处80 W·m-2、100 W·m-2(Model 0在计算到第一个月时的熔岩管壁的热流密度值)及120 W·m-2的热流密度边界,其他均为绝热的边界条件.另外由于水和其他挥发物可能存在于极地地区的冷阱中(Fisher et al., 2017; Li et al., 2018; Williams et al., 2019; Hoshino et al., 2020),因此我们也计算了极地地区熔岩管内建立科研站加热到宜居温度所需要的时间,将整个模型初始温度设置为110 K(Fisher et al., 2017; Li et al., 2018; Williams et al., 2019; Hoshino et al., 2020 ).

对于第二阶段的模型Model 0(图2b),我们主要考虑位于赤道地区的熔岩管,由于我们关注的重点不是月表,因此上表面采用赤道地区的平均温度215.5 K(Williams et al., 2017).Apollo 15和17的月球表面热流测量值分别为21 mW·m-2和16 mW·m-2(Langseth et al., 1972, 1976; Keihm and Langseth, 1973),考虑并校正后了局部热流效应后的全球平均热流为12 mW·m-2(Rasmussen and Warren, 1985; Warren and Rasmussen, 1987).因此我们根据月球全球平均热流值12 mW·m-2(Rasmussen and Warren, 1985; Warren and Rasmussen, 1987),月表风化层热导率0.0015 W·(m·K)-1(Prasad, 2020; Lozano, 2016),赤道地区的平均温度215.5 K(Williams et al., 2017)以及玄武岩层热导率2 W·(m·K)-1(Molaro et al., 2017),利用公式(2)分别计算了风化层和玄武岩层温度随深度的变化(如表2所示)并且得到模型底部恒温边界条件的温度值(如表3所示).

表2 第二阶段模型初始温度场的设置Table 2 Models initial temperature fields setting in the second stage

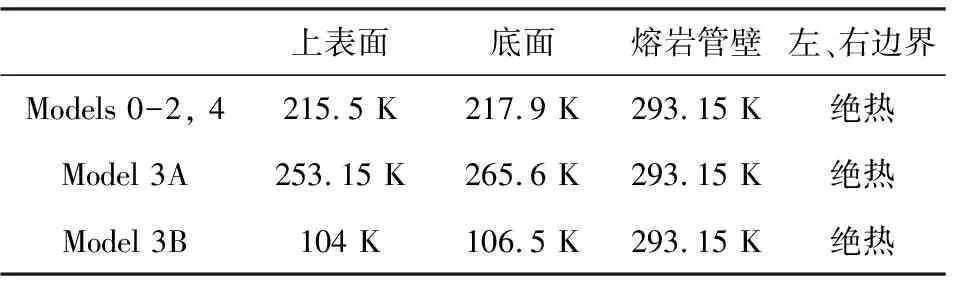
表3 第二阶段模型边界条件的设置Table 3 Models boundary conditions setting in the second stage

对于第二阶段模型除Model 0之外,我们在Model 0的基础上还设计了5个参考模型,参考模型的宽度和深度均与Model 0一致(600 m×300 m).其中,Models 1-2均位于赤道地区,其初始温度场设置和边界条件均与Model 0一致,仅仅是熔岩管的几何大小和深度与Model 0不同.具体来讲,Model 1熔岩管洞顶到表面为40 m,洞直径为20 m;Model 2洞顶到表面为20 m,洞直径为40 m.Model 3A位于赤道地区,其上表面设置为比赤道地区平均温度更高的253 K的恒温边界.Model 3B位于极地地区,上表面平均温度为104 K(Williams et al.,2017)的恒温边界.由于风化层的导热系数很低,相当于隔热层,因此我们在Model 0的基础上在熔岩管壁处增加0.5 m厚的风化层作为Model 4进行计算.参考模型的Model 3A和Model 3B与Model 0的温度场和底边界恒温边界温度值的计算方法一致,具体设置如表2—3所示.

总体来讲,在第二阶段上下表面均设置为恒温边界条件,熔岩管壁为人类宜居的293.15 K,左右边界均为绝热边界条件(表3).

3 模拟结果

3.1 第一阶段——熔岩管的加热时间

由于下边界热流密度值的大小影响熔岩管加热到宜居温度的时间快慢,因此我们给定不同的热流密度值计算了Apollo测量点初始均匀温度为250 K(Apollo 15和17测量得出月表以下深度超过50 cm处的平均温度)以及极地地区熔岩管壁在加热阶段温度随时间的演化过程(图3—4).

图3 初始温度为250 K时模型中点随时间的温度变化A—E为从熔岩管壁处沿径向方向的点,到熔岩管壁的径向距离分别为d=0 m,1 m,2 m,5 m,10 m. 具体位置如图2a红色圆点所示. (a) 底部边界热流密度为80 W·m-2; (b) 底部边界热流密度为100 W·m-2;(c) 底部边界热流密度为120 W·m-2.Fig.3 Temperature variation of five points in the model with time when the initial temperature is 250 KA—E are points from the lava tube wall to the radial direction, and the radial distance to the lava tube wall is d=0 m, 1 m, 2 m, 5 m, 10 m. The specific location is shown in the red dot in Fig.2a. (a) The bottom boundary heat flux is 80 W·m-2; (b) The bottom boundary heat flux is 100 W·m-2; (c) The heat flux at the bottom boundary is 120 W·m-2.

图3中,我们给定了初始温度为250 K的均匀温度场.随着时间的增大,底边界处的点温度首先升高,距离下边界越远温度升高得越慢(图3).在热流密度边界为80 W·m-2时大约12天就可以将熔岩管壁加热到293.15 K的宜居温度(图3a),而热流密度边界为100 W·m-2时仅需要7天就可以将熔岩管壁加热到293.15 K的宜居温度(图3b).热流密度边界为120 W·m-2时仅需要5天就可以将熔岩管壁加热到293.15 K的宜居温度(图3c).

由于100 W·m-2的热流密度相当于给定熔岩管壁恒定的加热功率,而熔岩管的加热功率是通过其热流密度乘以熔岩管壁的周长来计算的,因此单位轴向长度的熔岩管在初始时刻需要6280 W·m-1(100 W·m-2×π×20 m)的加热功率.对于直径为20 m的熔岩管初始时刻采用6280 W的加热功率大约7天就可以将熔岩管加热到293.15 K的宜居温度.由于我们没有考虑真实熔岩管的散热问题,7天的加热时间只是一个最低估计.

图4中,我们计算了当极地地区的初始温度为110 K时,熔岩管加热到可居住温度所需的时间.在热流密度边界为220 W·m-2时,1个月的时间可以将熔岩管壁加热到290 K(图4a).热流密度边界为260 W·m-2时,23天就可以将熔岩管壁加热到293.15 K宜居温度(图4b).热流密度边界为280 W·m-2时,大约19天就可以将熔岩管壁加热到293.15 K的宜居温度(图4c).

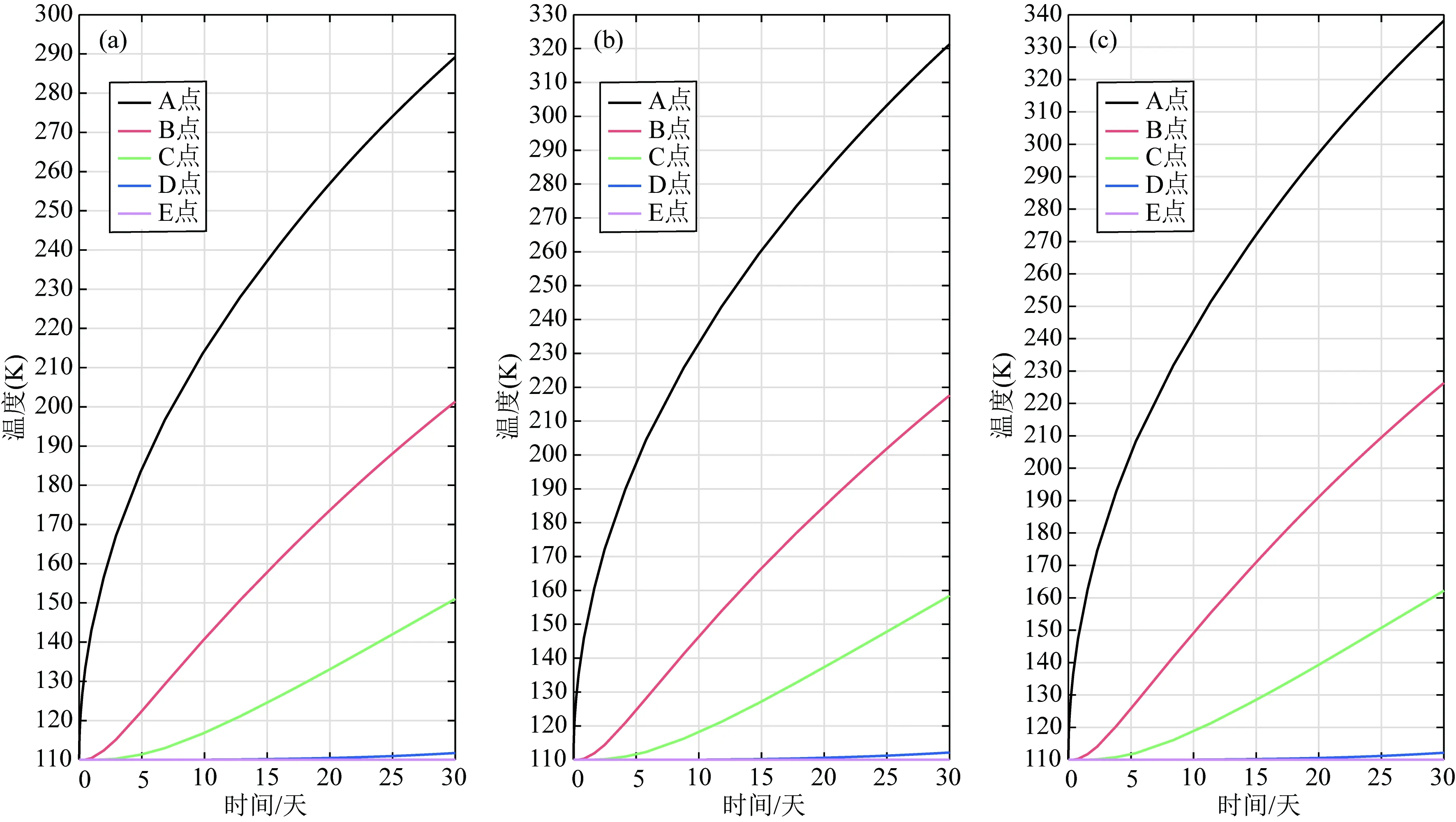
图4 初始温度为110 K时模型中点随时间的温度变化A—E为从熔岩管壁处沿径向方向的点,到熔岩管壁的径向距离分别为d=0 m,1 m,2 m,5 m,10 m. (a) 底部边界热流密度为220 W·m-2; (b) 底部边界热流密度为260 W·m-2; (c) 底部边界热流密度为280 W·m-2.Fig.4 Temperature variation of five points in the model with time when the initial temperature is 110 KA—E are points from the lava tube wall to the radial direction, and the radial distance to the lava tube wall is d=0 m, 1 m, 2 m, 5 m, 10 m. (a) The bottom boundary heat flux is 220 W·m-2; (b) The bottom boundary heat flux is 260 W·m-2; (c) The heat flux at the bottom boundary is 280 W·m-2.

因此对于位于极地地区的直径为20 m的每单位轴向长度的熔岩管在初始时刻需要16328 W·m-1(260 W·m-2×π×20 m)的加热功率,在大约23天内可以将熔岩管加热到宜居温度.

总之,下边界的热流密度越大,熔岩管壁温度升高的越快,区域温度值增大的也越快.熔岩管壁处的温度在一个月内仅仅可以向月表方向影响5 m左右,未影响到月表.

3.2 第二阶段——熔岩管维持热量所需热功率的模型演化结果

风化层在深度超过50 cm的区域的温度在～250 K时保持恒定(Langseth and Keihm, 1977; Heiken et al., 1991),非常寒冷,不适宜人类居住.因此在月球建立熔岩管内的科研基地需要考虑熔岩管热量维持所需加热功率的问题,不同于第一阶段模型给定熔岩管壁为热流密度边界条件,这一阶段的模型我们给定熔岩管壁为恒温的293.15 K边界条件.

图5展示了Model 0温度场随时间的演化结果.由于熔岩管壁是恒温的293.15 K的边界条件,熔岩管壁的温度比其围岩玄武岩的温度高,因此热量从熔岩管壁向四周传递.在第3个月到第6个月中,熔岩管四周温度显著增加的区域较小,主要是靠近熔岩管的四周温度较高,热量传递还未影响到风化层(图5a—b).当加热时间持续一年时,熔岩管附近的热量传递范围在第6个月的基础上进一步扩大,但依旧没有传递到风化层(图5c).在第10年时,熔岩管附近的热流传递到风化层附近且温度向熔岩管上方传递得更快,这主要是受到风化层的影响.由于风化层具有极低的导热系数,因此风化层相当于绝热层抑制了热流的传递,故而熔岩管上方的温度较高(图5d).在100年时,熔岩管附近的热流向四周进一步传递,温度增加区域的范围进一步扩大,但还没有到达左右边界(图5e).在1000年时,熔岩管附近的热流传递到左右边界处,且向深部传递到底边界(图5f).在第100年和1000年处,可以更明显地看出受风化层的影响,熔岩管上方的温度较四周更高(图5e—f).

图5 Model 0温度场随时间的演化图(a) t=3个月; (b) t=6个月; (c) t=1年; (d) t=10年; (e) t=100年; (f) t=1000年.Fig.5 Evolution diagram of Model 0 temperature field with time(a) t=3 months; (b) t=6 months; (c) t=1 year; (d) t=10 years; (e) t=100 years; (f) t=1000 years.

为了计算熔岩管维持热量所需的热功率,首先需要计算总热流密度.图6展示了总热流密度随时间的演化结果.第3个月时,熔岩管的总热流密度向四周传递,但熔岩管壁的总热流密度最大(图6a).到第6个月和1年时,总热流密度进一步向四周传递(图6a—b).在第10年时,总热流密度传递到风化层表面,由于风化层的导热系数较小相当于绝热层阻碍了熔岩管壁总热流密度向风化层传递,因此熔岩管壁到风化层之间的总热流密度值较小(图6d).在100年时,总热流密度进一步向四周传递(图6e),到1000年时总热流密度进一步向熔岩管壁两侧传递,并且向更深处传递(图6f).由于风化层阻碍了热流向浅层传递,因此风化层与熔岩管壁之间的总热流密度向浅部传递时逐渐减小,且熔岩管壁上方靠近风化层附近处的总热流密度比周围的热流密度小(图6f).

图6 Model 0总热流密度随时间的演化图(a) t=3个月; (b) t=6个月; (c) t=1年; (d) t=10年; (e) t=100年; (f) t=1000年.Fig.6 Evolution of total heat flow of Model 0 with time(a) t=3 months; (b) t=6 months; (c) t=1 year; (d) t=10 years; (e) t=100 years; (f) t=1000 years.

总体上随着时间的增加,熔岩管壁及周围的总热流密度虽然在向四周传递,但是其总热流密度值随着时间的增加在逐渐减小(图6a—d).

4 讨论

在第二阶段Model 0的基础上,我们设计了5个参考模型(表2—3)来讨论熔岩管的加热功率.我们还考虑了不同深度、大小和纬度的熔岩管对加热功率的影响以及维持热量及生活用电所需多少太阳能电池板.

4.1 熔岩管维持热量所需的加热功率

图7展示了单位轴向长度的熔岩管壁的加热功率值随时间的变化量.因此,在刚开始应该给熔岩管一个较大的加热功率,在之后考虑较小的加热功率供热.从图7中可以看出,加热功率随时间逐渐降低,在100年以前降低的幅度比较大,100年以后到1000年降低的比较缓慢.

图7 单位轴向长度的熔岩管壁处的加热功率随时间的变化量Fig.7 Variation of heating power with time at lava tube wall per unit axial length

图7a中,前5个月的加热功率随时间变化幅度较大,意味着初始时刻熔岩管需要较大的加热功率.在5个月之后可以考虑使用较小的加热功率.如果考虑月球科研站的使用时间是100年,熔岩管的轴向长度为L(m),对于位于赤道地区的Model 0前5年仅仅需要800L～7000LW的功率来维持熔岩管的温度,5年到100年之间考虑使用300L～800LW 的功率加热熔岩管.

Model 1和Model 0相比,对于单位轴向长度的熔岩管初始时刻Model 0需要更大的功率7000 W·m-1,但在第三个月之后二者差异不大(图7a).而且赤道地区7000 W·m-1(Model 0)的加热功率与Apollo站在初始加热阶段6280 W·m-1的加热功率值相差不大,这也说明初始阶段采用7000 W·m-1的加热功率在大约7天内就可以将赤道地区每单位轴向长度直径为20 m的熔岩管加热到室温.因此同一直径深度越深处的熔岩管在初始时刻仅仅需要较小的加热功率就可以维持宜居温度.Model 2和Model 0相比,前5年尤其是第1个月到第三个月间需要较大的功率,5年之后Model 2和Model 0所需的功率均有所减小,二者差异也有所减小,但是总体上同一深度直径更大的熔岩管所需要的加热功率比直径更小的熔岩管维持热量所需要的功率更大(图7a—b).Model 3A和Model 0相比,由于Model 3A的上表面温度为253 K比Model 0高,说明位于赤道区域温度较高处的熔岩管所需要维持热量的加热功率更低.Model 3B与Model 3A和Model 0相比,由于极地地区平均温度比赤道地区低的多,所以位于极地区域的熔岩管所需要维持热量的加热功率更高(图7).

由于风化层具有极低的导热系数,因此在Model 0的基础上如果考虑添加风化层作为绝热层,可以阻碍热量的流失.可以看出,图7a—d中Model 4所需要的加热功率很小,为了更清楚地表示其加热功率的变化,将其展示在图7e—f中.在初始时刻,Model 4比Model 0的加热功率小一个数量级(图7a和7e).由此可见,Model 4和其他模型相比仅仅需要较小的加热功率就可以维持熔岩管的宜居温度.Model 4中,前2年需要较大的加热功率,如果考虑单位轴向长度的熔岩管需要20～120 W·m-1之间的功率供热(图7e).在2年到100年之间,仅仅需要较小的加热功率,大约为13～15 W·m-1的电炉供热就可以维持熔岩管的宜居温度(图7f).

由于我们的模型为二维模型且忽略了端部的三维散热效应,我们的模型计算结果仅可以提供最低能源供应的量级.

4.2 熔岩管的单位空间加热功率

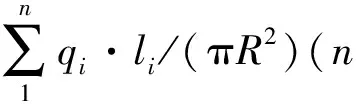
图8中,单位空间加热功率随时间逐渐减小,前5个月的单位空间加热功率普遍较大(图8a).而在5年到100年时,单位空间加热功率减少为大约第5年时的一半(图8b—c),100年之后熔岩管的单位空间加热功率进一步减小(图8d—e),因此可以考虑减小功率来供热以便节约能源.

图8 单位轴向长度的熔岩管壁处的单位空间加热功率随时间的变化量Fig.8 Variation of heating power per unit space with time at lava tube wall per unit axial length

此外,熔岩管的直径也是影响熔岩管单位空间加热功率的重要因素.Model 2和Model 0相比,深度相同、直径较大的熔岩管单位空间的加热功率比直径较小的熔岩管的单位空间加热功率小.对于含绝热层的Model 4,单位空间的加热功率相较于其他模型均较小,在前2年时单位空间加热功率随时间剧烈地减小(图8e),在大约2年之后单位空间加热功率随时间变化几乎保持恒定值(图8e—f).

总而言之,只有在前3个月,同一直径和同一深度的熔岩管的单位空间加热功率和加热功率均小于深度较小的熔岩管.在4个月后,深度对熔岩管的单位空间加热功率和加热功率影响并不显著.此外,深度相同、直径较大的熔岩管的加热功率大于直径较小的熔岩管,而直径较大的熔岩管的单位空间加热功率小于直径较小的熔岩管.在极地地区,熔岩管的加热功率和单位空间加热功率均大于赤道地区.当月表温度为250 K时,同一直径同一深度的熔岩管的单位空间加热功率和加热功率均小于赤道地区.考虑到节省能源损耗,我们建议月球研究站应该建立在位于赤道温度较高、深度较深、直径较大的熔岩管中.如果考虑进一步节省能源,我们建议在熔岩管壁上添加0.5 m厚的风化层作为隔热层,以防止热量损失.

4.3 熔岩管的电热供给

4.3.1 太阳辐射热能

在月球上建立科研基地还需要考虑电能的供给问题,由于月球上没有大气层,因此相较于地球,月球有着丰富的太阳能且太阳能可以有效节省能源,因此采用太阳能供电是我们的首选方式.

为了采用太阳能电池板供热,首先我们需要计算月球上太阳能电池板可接受到的太阳辐射光能.月表太阳吸收热量的计算公式(Hayne et al., 2017)如下:

QS=(1-A)I,

(3)

其中,QS为月表吸收太阳光照的热通量,A为月表太阳光反射率,I为有效太阳辐照度(单位:W·m-2).

由于具有绒面结构的晶硅太阳能电池的反射率为9.04%(赵燕,2020),因此我们选取A=0.09进行计算.

有效太阳辐照度I的计算公式如下(李雄耀等,2008):

(4)

其中,S0为太阳常数,Rsm为相对于1 AU的无量纲日月距离,z0为太阳天顶角的度数.S0=1361 W·m-2,Rsm=1.0 (Miller and Turner, 2009).

由于月球没有大气层,一个月球日(29.5天=2.5488×106s)内接近一半时间可以利用太阳能.如果不考虑地形的影响,采用始终保持垂直于太阳光照射的可移动太阳能电池板以接收最多的太阳辐射能量,则公式(4)中z0=0°.对公式(3)关于半个月球日的时间积分可得到垂直于太阳光照射的可移动太阳能电池板一个月球日内可获得的太阳辐射热能为1.58×109J·m-2.由于目前使用较为广泛的单晶硅太阳能电池的光电转换率为24.7%(成志秀和王晓丽,2007),因此一个月球日内太阳辐射能转换为电能大约为3.9×108J·m-2.如果考虑使用碳纤维电热板加热熔岩管,由于其电热转换率为0.948(谭羽非和赵登科,2008),则一个月球日内的太阳能电池板可获得的太阳辐射能转换为热能为～3.7×108J·m-2.

4.3.2 供热用电

在加热阶段,在Apollo测量点直径为20 m的单位轴向长度的熔岩管,如果初始时刻采用7000 W·m-1的电炉在半个月(地球日)内就可以将熔岩管加热到293.15 K的宜居温度,而一个月球日内只有一半时间可以接受到太阳辐射,因此在半个月内所产生的热能为8.92×109J·m-1(7000 (W·m)-1×半个月球日).如果考虑实际熔岩管的轴向长度为L,则直径20 m的熔岩管在半个月内所产生的热能为L×8.92×109J,需要 ～24Lm2的太阳能电池板.同样地,如果考虑到水资源的利用将科研站选在极地地区,则直径为20 m的熔岩管在一个月球日内产生的热能为L×2.17×1010J,需要60.2Lm2的太阳能电池板.

在第二阶段,赤道地区直径为20 m且洞顶深度为20 m的单位轴向长度的熔岩管(Model 0),如果要维持单位轴向长度的熔岩管在宜居温度,前5年需要的加热功率在1000～7000 W·m-1之间(图7a,b),需要3.4～24 m2的太阳能电池板.如果考虑科研站的使用寿命为100年,在5年之后,Model 0仅需要500～600 W·m-1的功率就可以维持熔岩管的宜居温度(图7c),则需要1.7～2.1 m2的太阳能电池板.因此如果要维持赤道地区直径为20 m的熔岩管在宜居温度,前5年需要3.4L～24Lm2的太阳能电池板给科研基地供电.在5年之后,仅需要1.7～2.1Lm2的太阳能电池板.

对于考虑加绝热层的Model 4,单位长度的熔岩管在前30个月需要20～120 W·m-1的加热功率维持在宜居温度,则需要0.06～0.4 m2的太阳能电池板.在这之后的100年内只需要大约15 W·m-1的加热功率,需要0.05 m2的太阳能电池板.对于实际轴向长度为L的熔岩管,需要的加热功率需要乘以熔岩管的轴向长度L,相应的太阳能电池板的面积也需要在计算值的基础上乘以L.

因此在维持人类宜居阶段,位于赤道地区直径为20 m且洞顶深度为20 m的轴向长度为L的熔岩管(Model 0)在前五年需要3.4L～24Lm2的太阳能电池板,在五年之后需要1.7L～2.1Lm2的太阳能电池板.对于位于赤道地区加绝热层的Model 4在前三年则需要0.06L～0.4Lm2的太阳能电池板,在三年之后需要0.05Lm2太阳能电池板.

5 结论

本文建立了二维瞬态热传导有限元数值模型,分别以熔岩管壁为热流密度边界条件和恒温的室温293.15 K为边界条件计算了熔岩管需要加热到室温需要耗费多长时间以及维持室温所需耗费的功率问题.由于我们的模型忽略了端部的三维散热效应,我们的模型计算结果仅可以提供最低能源供应的量级估计.模拟结果表明:

(1) 初始供热阶段,如果要将直径为20 m的单位轴向长度(1 m)的熔岩管加热到宜居温度,在Apollo测量点采用7000 W·m-1的电炉供热,7天就可以达到宜居温度(293.15 K);在极地地区采用17000 W·m-1的电炉供热,23天就可以达到宜居温度(293.15 K).如果考虑实际熔岩管的轴向长度为L(m),则直径为20 m的熔岩管在第一个月球日期间在赤道地区需要24Lm2的太阳能电池板,在极地地区需要60.2Lm2的太阳能电池板.

(2) 维持热量阶段,当熔岩管壁为室温293.15 K时,随着时间的演化热流向四周传递,由于风化层具有极低的导热系数阻碍了熔岩管壁处的温度向风化层传播,因此熔岩管壁上方的温度较高.熔岩管壁处的总热流密度在向四周传递的同时也在随着时间的增加而逐渐减小.风化层阻碍了总热流密度向浅层传递,导致风化层与熔岩管壁之间的总热流密度向浅部传递时逐渐减小.

(3) 不同纬度、不同深度以及不同大小的熔岩管所需要的加热功率以及单位空间加热功率不同.计算结果表明,月球科研站应该选在赤道地区温度较高且深度更深、直径较大的熔岩管处更加节省能源.如果考虑进一步节省能源,我们建议在熔岩管壁处增加0.5 m厚的风化层作为绝热层阻碍热量的流失.如果考虑到水资源的利用,建议将科研站选在位于极地地区的熔岩管.

(4) 如果考虑在赤道区域选择洞顶距离表面20 m、洞内直径20 m且洞壁加0.5 m厚的风化层作为绝热层的熔岩管作为科研基地,在前3年熔岩管需要20L～120LW的加热功率来维持熔岩管的宜居温度,仅需要0.06L～0.4Lm2的太阳能电池板.在3年到100年之间,仅仅需要大约15LW就可以维持熔岩管的宜居温度,只需要0.05Lm2的太阳能电池板.