正反向结合灰自助滤波法在滚动轴承性能可靠性评估中的应用

米月花, 马梦华, 庞晓旭

(1. 郑州商学院 信息与机电工程学院,河南巩义 451200;2. 河南科技大学 机电工程学院,河南洛阳 471003)

滚动轴承作为旋转机械的关键性基础部件,其性能可靠性直接影响旋转机械的寿命及性能可靠性。因此,对滚动轴承性能可靠性进行评估具有不可或缺的意义[1-3]。

滚动轴承在服役过程中受到各种影响因素的干扰,如何区分干扰信号和有效信号给轴承性能可靠性的评估带来很大的挑战。现有的滤波算法主要有滚动均值法[4]、中位值平均滤波法[5]、限幅滤波法[6]等。但是,这些算法在滤除干扰信号的同时也改变了滚动轴承的性能概率密度函数,进而可能会影响到轴承性能可靠性的精准评估。自助法[7-8]可以在不改变轴承性能概率密度函数的同时通过生成大量样本数据抑制干扰信号的影响;灰预测模型[9-10]通过连续迭代、不断更新样本,进而充分利用样本的有效信息。灰自助滤波法融合了自助法和灰预测模型的优点,而正反向结合灰自助滤波法集结了正向灰自助滤波法和反向灰自助滤波法的优势,能够对轴承性能可靠性进行更加精准地评估。

现有研究通常通过比较滤波前后两个序列的线性相关系数或者非线性灰关联度对滤波效果进行检验,并没有考虑滤波过程中轴承性能概率密度函数是否发生改变。鉴于此,本文运用概率密度函数交集法[11-12],通过计算滤波前后两个序列概率密度函数的交集面积,检验正反向结合灰自助滤波法的效果好坏。在选定性能阈值后,基于泊松过程理论[13-14]求解各个振动数据序列的变异个数、变异概率和性能可靠度,从而分析滚动轴承在服役过程中的性能变化趋势。

1 数学模型

假设在试验期间采集到的轴承振动性能序列为

S=(s(1),s(2),…,s(i),…,s(I))i=1,2,…,I

(1)

式中:S为轴承振动加速度数据样本;s(i)为数据样本中的第i个振动加速度数据;I为振动加速度数据的总个数。

1.1 正反向结合灰自助滤波模型试验方法

灰自助滤波的中心思想是运用灰自助法和振动性能序列S中与t时刻紧邻时刻的前n(n≤t)个数据(包括t时刻的数据), 生成新的数据取代当前数据,减小数据样本中粗大误差对实验分析的影响,从而达到降噪的效果。

从振动性能序列S中等概率可放回地随机抽数据,每次抽取k个数据,重复抽取g次得到G个样本,构成一个新的序列S1,即

S1=(S1,S2,…,Sg,…,SG)

(2)

式中:g为自助样本的序号,g=1,2,…,G;Sg为自助再抽样得到的第g个自助样本。

Sg=(sg(1),sg(2),…,sg(I))

(3)

根据灰预测模型[9-10],得到一次累加生成数据样本Xg,表示为

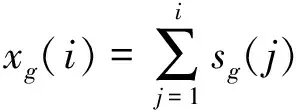
(4)

Xg=(xg(1),xg(2),…,xg(i),…,xg(I))

(5)

灰预测模型用微分方程表示为

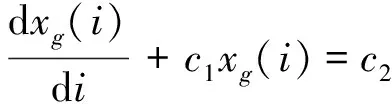
(6)

式中c1和c2为待定系数。

(7)

式中Δi取单位间隔1。

均值生成序列用Zg表示为

Zg=[zg(1),zg(2),…,zg(i),…,zg(I)]

(8)

式中zg(i)=[0.5xg(i)+0.5xg(i-1)]。

在初始条件xg(1)=yg(1)条件下,微分方程的最小二乘解表示为

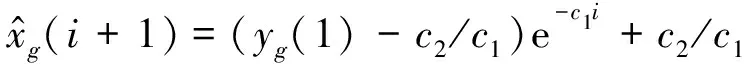
(9)

(c1,c2)T=(DTD)-1DT(Yg)T

(10)

D=(-Zg,E)T

(11)

Ε=(1,1,…,1)

(12)

累减生成数据样本用Xg表示为

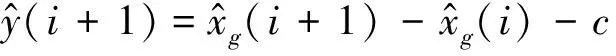
(13)

得到的正向灰自助滤波样本S1*表示为

(14)

将原序列S进行逆序排列,同样地运用灰预测模型进行处理,得到的反向灰自助滤波样本S2*表示为

(15)

融合正向灰自助滤波样本和反向灰自助滤波样本中的有效信息,得到的新的样本S*表示为

S*=S1*+S2*=

(16)

1.2 运用概率密度函数交集法检验滤波效果

基于最大熵法,计算滤波前原序列S的概率密度函数,用f0(s)表示为

(17)

式中:al0为滤波前原序列S的第l+1个拉格朗日乘子;l为原点矩的阶数,l=0,1,2,…,L,通常取L=5;q0和w0为滤波前原序列S的映射参数。

同样地计算正反向灰自助滤波样本S*的概率密度函数,用f1(s)表示为

(18)

式中:al1为正反向灰自助滤波样本S*的第l+1个拉格朗日乘子;q1和w1为正反向灰自助滤波样本S*的映射参数。

用滤波前原序列的概率密度函数f0(s)与正反向结合灰自助滤波样本的概率密度函数f1(s)的重合面积A表征该滤波方法的效果好坏。

g(s)=min(f0(s),f1(s))

(19)

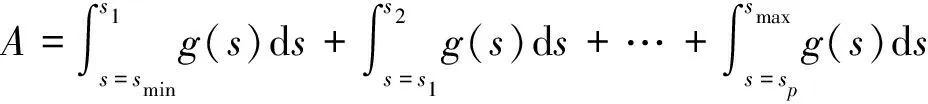
(20)

式中:smin和smax分别为性能序列的最小值和最大值;s1、s2、sp分别为概率密度函数曲线f0(s)与f1(s)的第1、2、p个交点的横坐标值。

重合面积A越大表示该滤波方法的效果越好;反之,该滤波方法的效果越差。

1.3 基于泊松过程计算性能可靠度

设定性能阈值V,记录正反向灰自助滤波样本S*中的数据落在阈值区间[-v,v]之外的个数N,进而计算数据序列对应时间段内的变异概率λ。

(21)

基于泊松过程理论,计算轴承运转过程中的性能可靠度,用R(λ)表示为

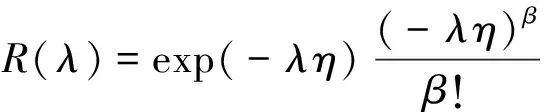
(22)

式中:η为时间变量;β为失效事件发生的次数。

因此,η=1且β=0对应轴承性能尚未失效的可靠度R。

R=exp(-λ)

(23)

λ越大表示滚动轴承性能变异程度越严重,性能可靠度也越低;反之,滚动轴承性能变异程度越轻,性能可靠度越高。

2 试验研究

2.1 案例1

实验数据来源于美国Case Western Reserve University的轴承数据中心网站,实验在专用的滚动轴承故障模拟实验台上进行[2]。实验所用轴承型号为SKF6205,在速度为1 797 r/min、采样频率为12 kHz条件下,采集滚动轴承内圈沟道磨损直径D分别为0,0.177 8,0.533 4和0.7112 mm时的振动加速度数据序列,滚动轴承振动加速度数据序列如图1所示。

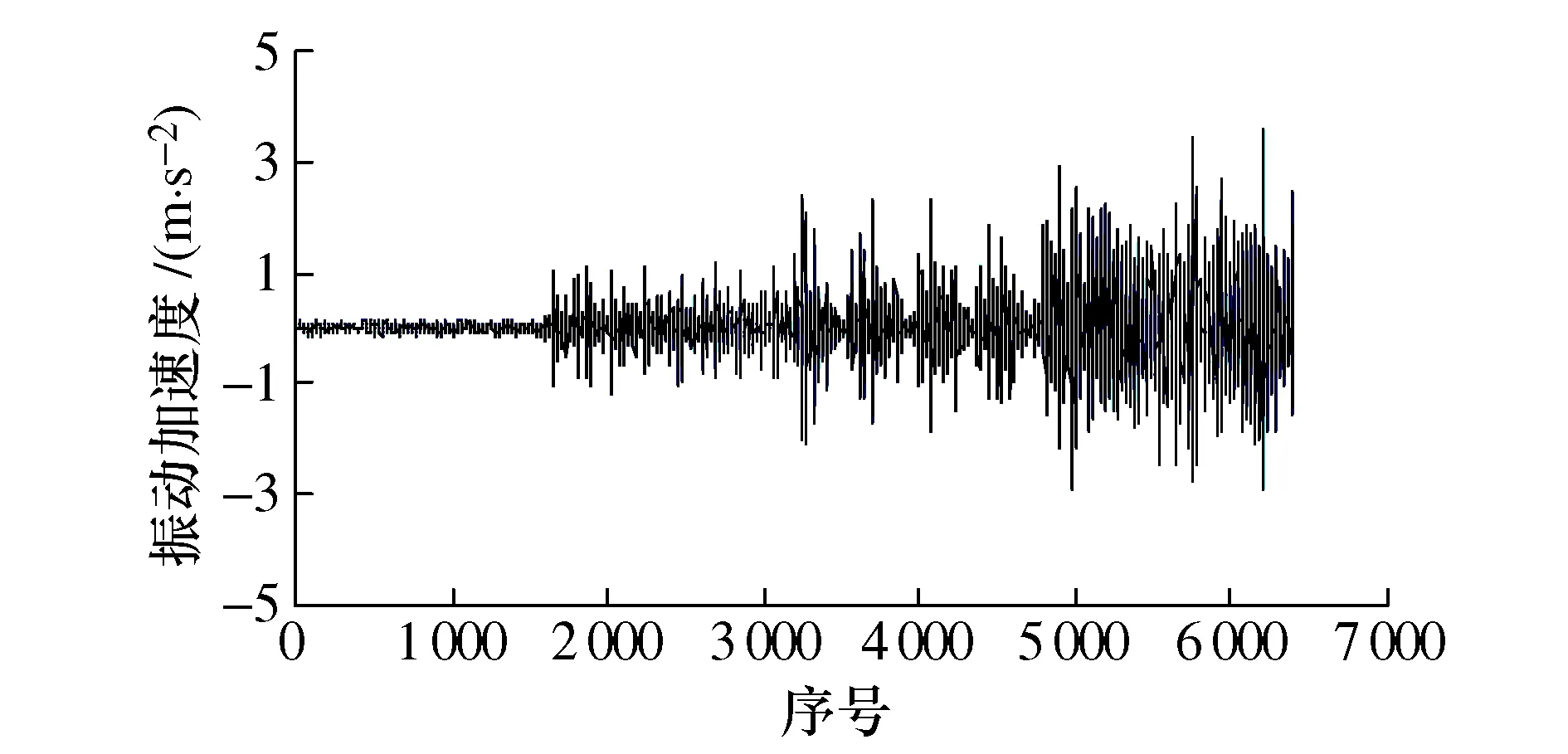
图1 滚动轴承振动加速度数据序列Fig.1 Vibration acceleration data sequence of rolling bearing

由图1可知,滚动轴承内圈沟道磨损直径D为0时(对应第1～1 600个数据)的振动数据波动最小,数值在区间[-0.175 7, 0.179 8]m/s-2内波动;磨损直径D为0.177 8 mm时(对应第1 601～3 200个数据) 的振动数据波动有所增大, 数值在区间 [-1.181 2, 1.203 8]m/s2内波动;磨损直径D为0.533 4 mm时(对应第3 201～4 800个数据)的振动数据波动又有所增大,数值在区间[-2.065 7, 2.375 6] m/s2内波动;磨损直径D为0.711 2 mm时(对应第4 801～6 400个数据)的振动数据波动最大,数值在区间[-2.941 1, 3.564 9] m/s2内波动。随着滚动轴承内圈磨损直径的增大,振动数据波动也越来越剧烈,间接表明该轴承的振动性能退化程度随着磨损直径的增大越来越严重。为了叙述方便,将磨损直径D为0时的振动数据序列记为第1数据序列;将磨损直径D为0.177 8 mm时的振动数据序列记为第2数据序列;将磨损直径D为0.533 4 mm时的振动数据序列记为第3数据序列;将磨损直径D为0.711 2 mm时的振动数据序列记为第4数据序列。

基于灰自助滤波法,对4个数据序列数据样本进行处理,结果如图2～图5所示。

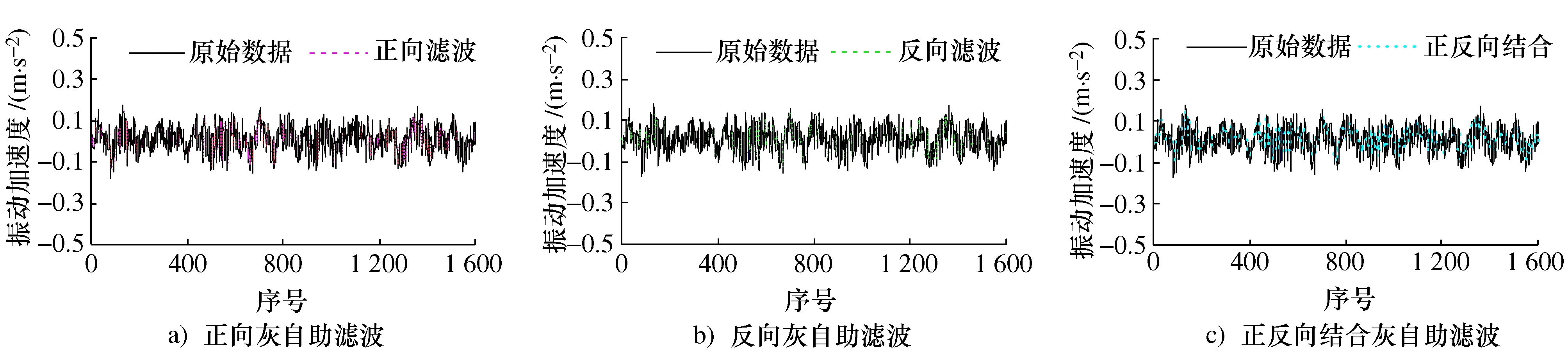
图2 第1数据序列的滤波结果Fig.2 Filter results of the first data sequence

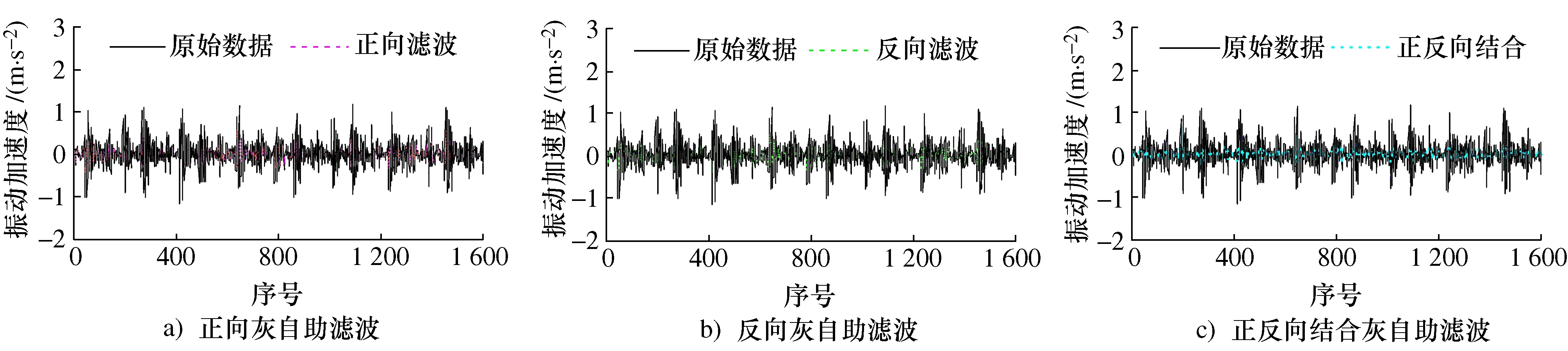
图3 第2数据序列的滤波结果Fig.3 Filter results of the second data sequence

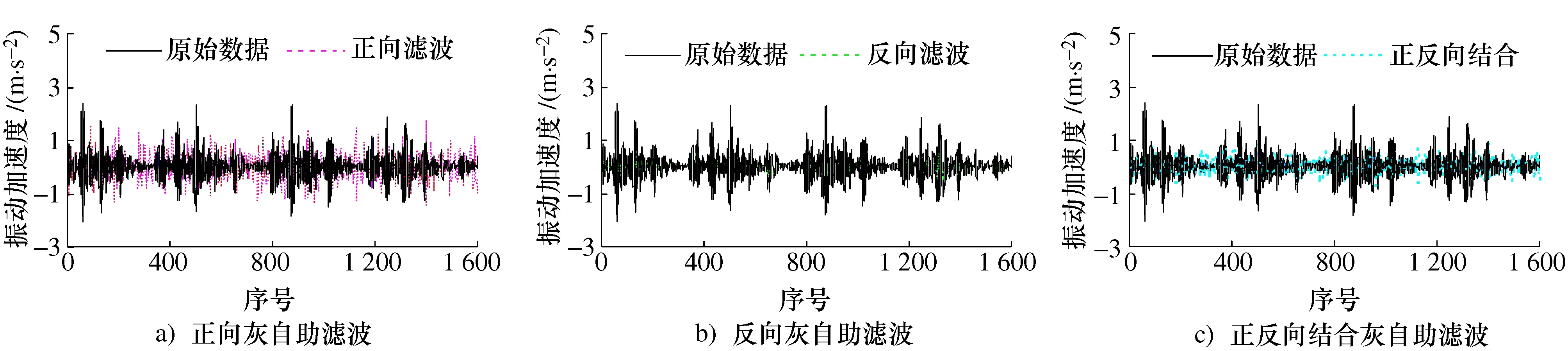
图4 第3数据序列的滤波结果Fig.4 Filter results of the third data sequence

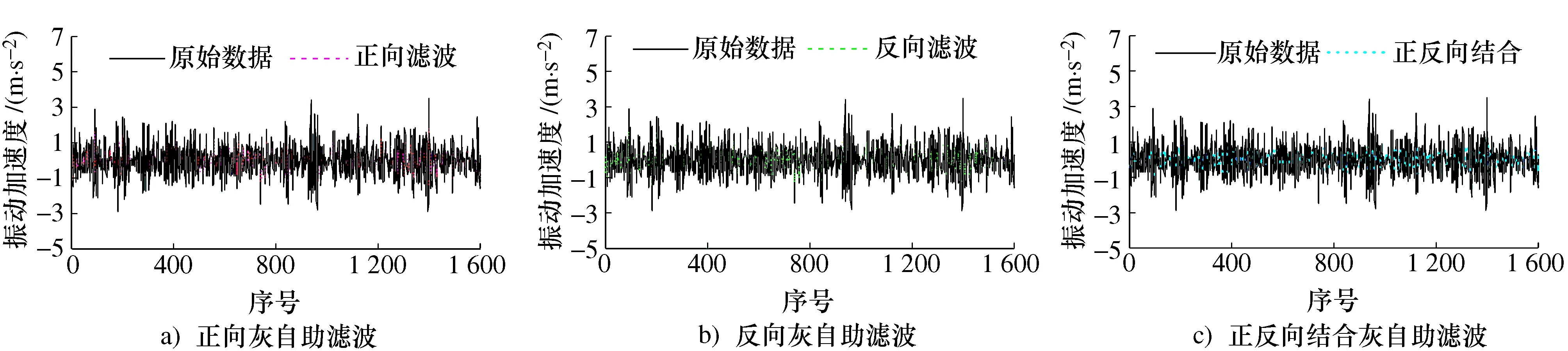
图5 第4数据序列的滤波结果Fig.5 Filter results of the fourth data sequence

以第1数据序列为例,基于最大熵法计算滤波前后该数据样本的拉格朗日乘子,如表1所示。接着,求解其概率密度函数,滤波前后第1数据序列的概率密度函数如图6所示。

图6 滤波前后第1数据序列的概率密度函数Fig.6 Probability density functions of the first data sequence before and after filtering

由图6可知,滚动均值滤波后的数据样本与滤波前数据样本概率密度函数的交集面积最小,即该种方法的滤波效果最差。正反向结合滤波方法的效果最好,正向滤波方法的效果次之。下面计算滤波后数据样本的概率密度函数与滤波前数据样本概率密度函数的重合面积,进而对滤波效果进行定量分析,结果如表2所示。

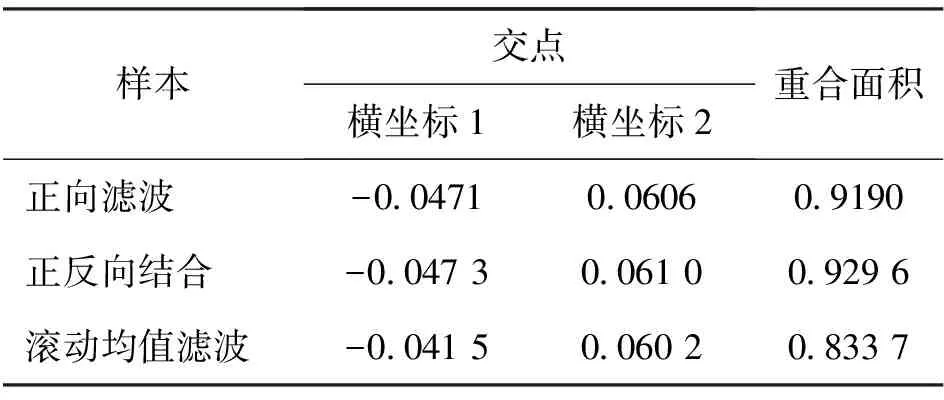
表2 滤波前后各个概率密度函数的重合面积(案例1)Tab.2 Overlapped areas of probability density functions before and after filtering(case 1)

由表2可知,正向灰自助滤波方法和正反向结合灰自助滤波方法的滤波效果均比滚动均值滤波方法的效果好很多。正反向结合灰自助滤波方法比正向灰自助滤波方法的效果要好,这是因为其融合了正向灰自助滤波方法和反向灰自助滤波方法的优点。

取振动加速度阈值为0.4 m/s,计算各个振动序列对应时间段内的变异个数、变异概率以及可靠度,结果如表3所示。

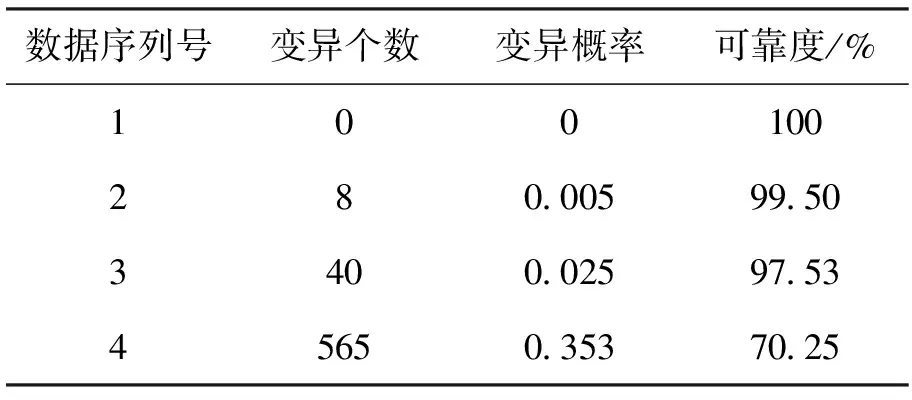
表3 各个振动序列的变异个数、变异概率可靠度(案例1)Tab.3 Variation number, variation probability and reliability of different vibration sequences(case 1)

滚动轴承振动性能可靠性随着内圈沟道磨损直径的变化而变化的具体规律,如图7所示。

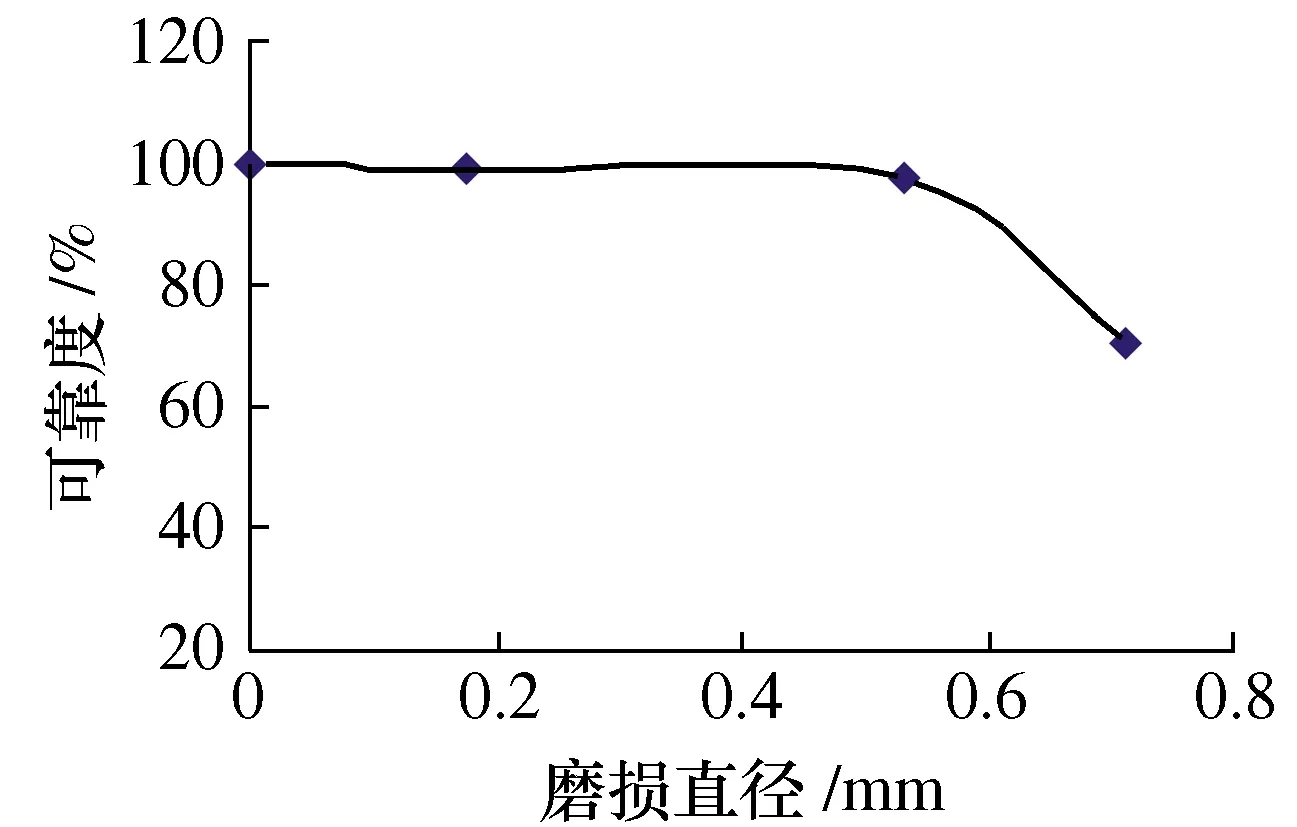
图7 振动性能可靠度与磨损直径的关系Fig.7 Relationship between vibration performance reliability and wear diameter

由图7可以看出,随着磨损直径的增大该滚动轴承的振动性能可靠性呈现非线性减小的趋势。磨损直径由0变化至0.177 8 mm的过程中,该滚动轴承振动性能可靠度从100%减小到99.50%;磨损直径由0.177 8 mm变化至0.533 4 mm的过程中,该滚动轴承振动性能可靠度从99.50%减小到97.53%;磨损直径由0.533 4 mm变化至0.711 2 mm的过程中,该滚动轴承振动性能可靠度从97.53%减小到70.25%。

在轴承振动性能可靠度降低至90%之前,应提前更换轴承或对其进行维护,安全起见,本案例中轴承应在内圈沟道磨损直径增大至0.6 mm之前进行更换,从而避免不必要的经济损失和人员伤亡。

2.2 案例2

实验数据来源于杭州轴承试验研究中心有限公司,分析滚动轴承在强化寿命实验过程中其振动性能可靠度变化过程。实验所用轴承为P2级角接触球轴承7008AC,在转速为4 000 r/min,径向力为4.17 kN、轴向力为4.58 kN条件下,每隔1 min采集一次滚动轴承外圈的振动加速度均方根值[15],滚动轴承振动加速度均方根序列如图8所示。

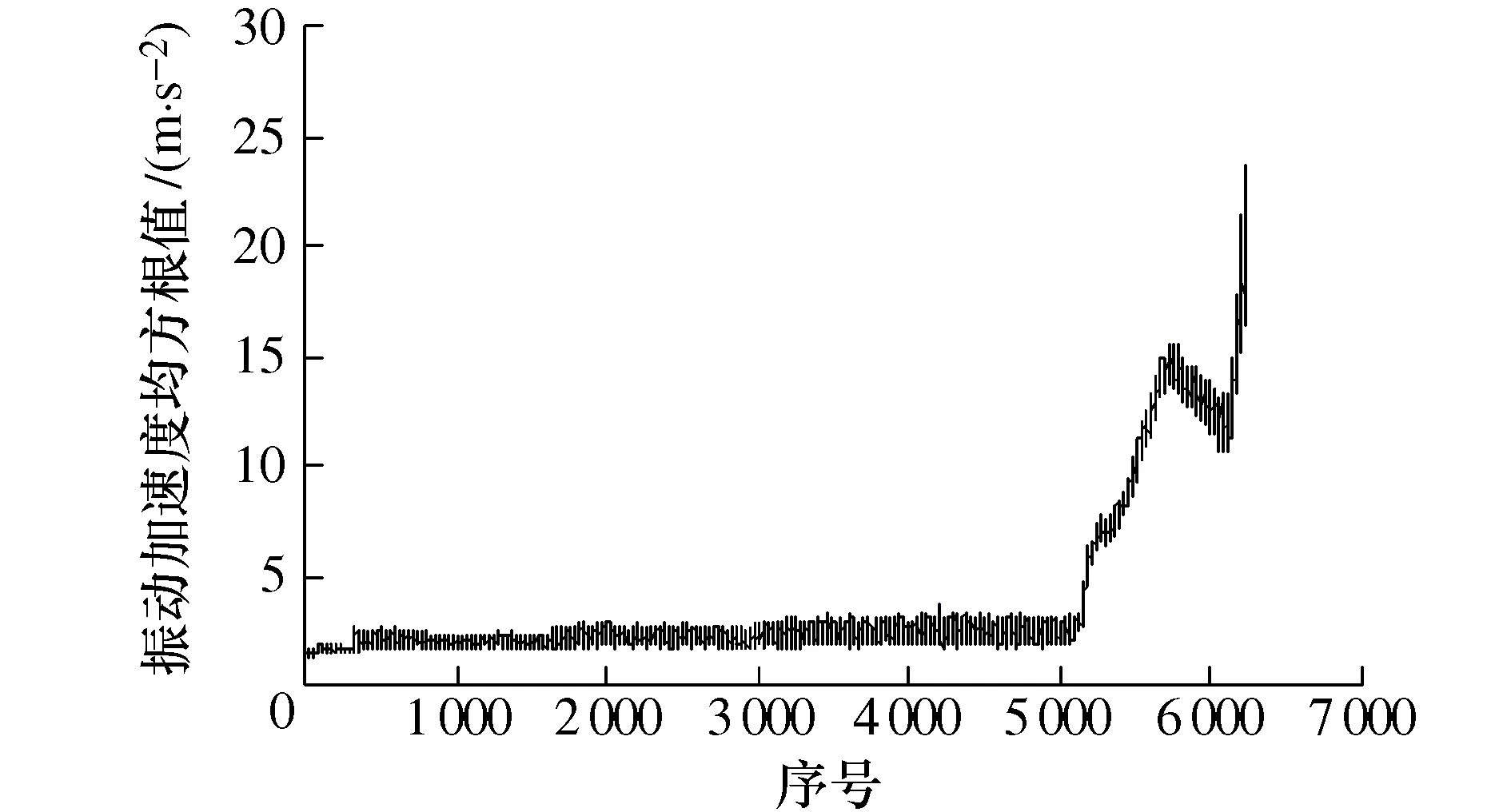
图8 滚动轴承振动加速度均方根序列Fig.8 Root-mean-square sequence of rolling bearing vibration acceleration

由图8可知,在第5 100个左右数据之前轴承振动性能相对较平稳,之后便进入迅速退化阶段,总体上呈现非线性退化的趋势。

基于灰自助滤波法,对该振动加速度均方根序列进行处理,各种滤波方法的结果如图9所示。

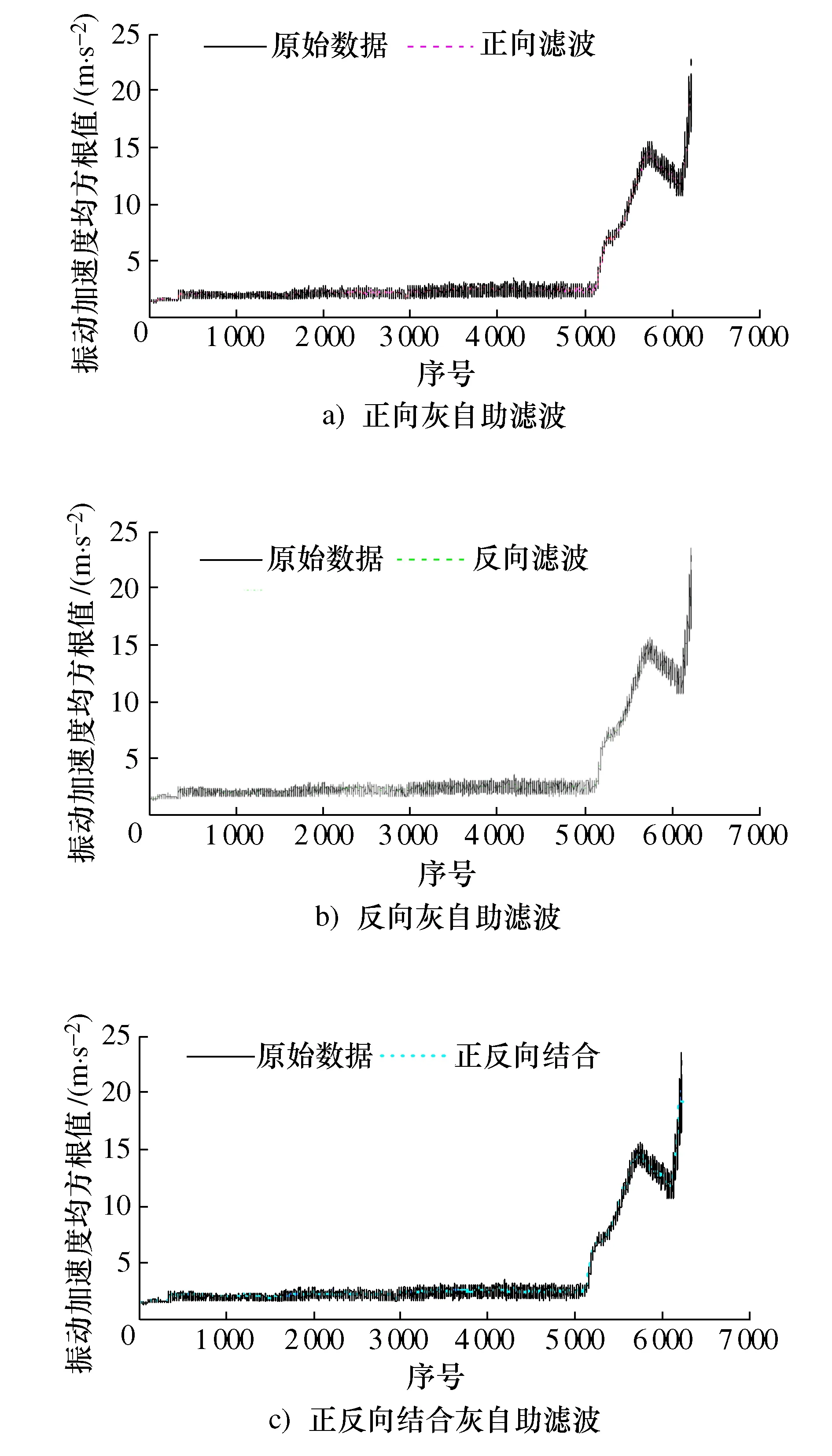
图9 各种滤波方法的结果Fig.9 Results on various filtering methods

由图9可知,各种滤波方法的效果均较好,究竟哪种方法的效果更好?下面基于概率密度函数交集法对其进行定量分析。

基于最大熵法计算滤波前后该数据样本的拉格朗日乘子,如表4所示。接着,求解其概率密度函数,滤波前后的概率密度函数如图10所示。

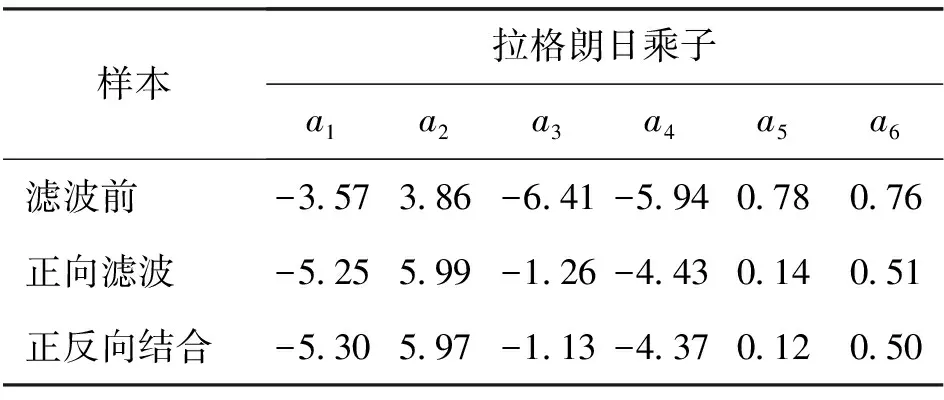
表4 各种滤波方法的拉格朗日乘子Tab.4 Lagrange multipliers of various filtering methods

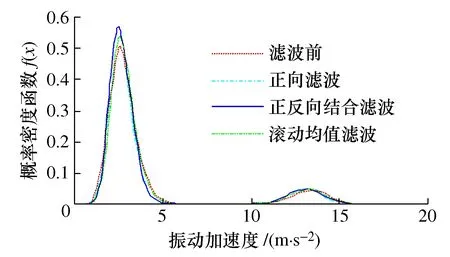
图10 滤波前后的概率密度函数Fig.10 Probability density functions before and after filtering

由图10可知,滚动均值滤波后的数据样本与滤波前数据样本概率密度函数的交集面积最小,即该种方法的滤波效果最差。正反向结合滤波方法的效果最好,正向滤波方法的效果次之。下面计算滤波后数据样本的概率密度函数与滤波前数据样本概率密度函数的重合面积,进而对滤波效果进行定量分析,结果如表5所示。

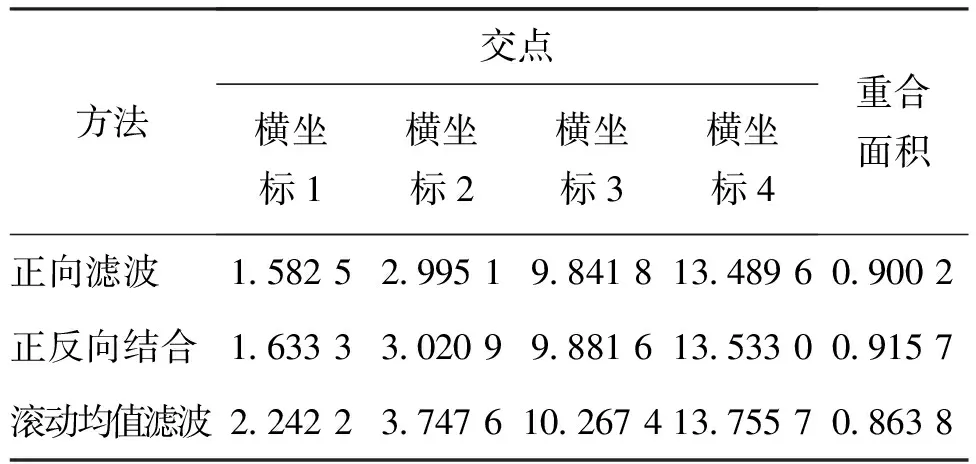
表5 滤波前后各个概率密度函数的重合面积(案例2)Tab.5 Overlapped areas of probability density functions before and after filtering (Case 2)

由表5可知,本案例中正向灰自助滤波方法和正反向结合灰自助滤波方法的滤波效果均比滚动均值滤波方法的效果好很多。正反向结合灰自助滤波方法比正向灰自助滤波方法的效果要好,这是因为其融合了正向灰自助滤波方法和反向灰自助滤波方法的优点。

将轴承振动加速度均方根序列分为10份,取振动加速度阈值为10 m/s2,计算各个振动序列对应时间段内的变异个数、变异概率以及可靠度,结果如表6所示。

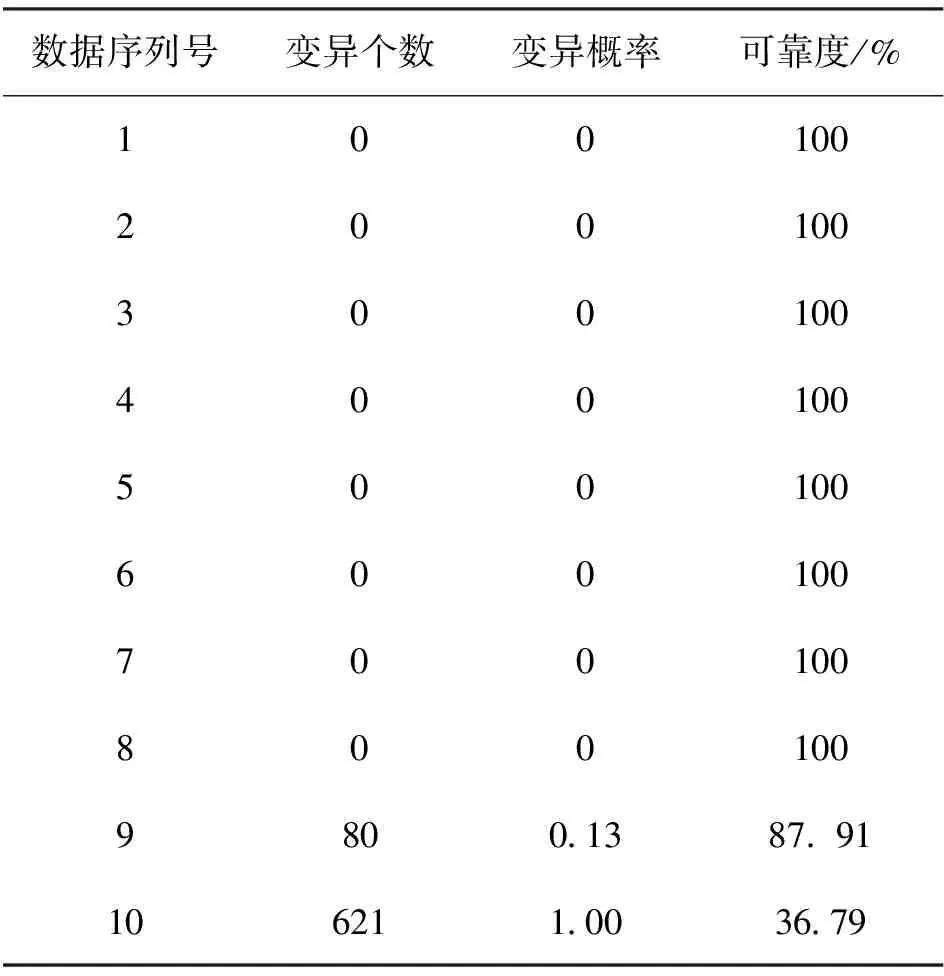
表6 各个振动序列的变异个数、变异概率可靠度(案例2)Tab.6 Variation number, variation probability and reliability of different vibration sequences (Case 2)

滚动轴承振动性能可靠性随着时间的变化而变化的具体规律,如图11所示。

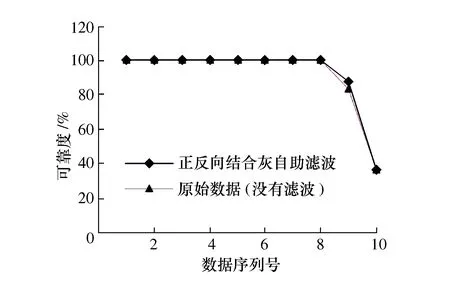
图11 轴承振动性能可靠度Fig.11 Vibration performance reliability of bearings

由图11可以看出,该滚动轴承的振动性能可靠性呈现非线性减小的趋势。在第8数据序列对应的时间点之前,轴承振动性能可靠度均为100%;在第8数据序列至第9数据序列对应的时间段之间,轴承振动性能可靠度缓慢下降,数值由100%减小至87.91%;在第9数据序列至第10数据序列对应的时间段之间,轴承振动性能可靠度快速下降,数值由87.91%减小至36.79%。而用原始数据直接计算时,第9数据序列对应的时间段内轴承振动性能可靠度更小,这是由于滤波前数据波动更大,计算出的轴承性能变异率更大。将两者进行对比可以发现,经过正反向结合灰自助滤波后,轴承性能退化曲线更光滑,即在突变点处性能可靠度变化值更小。

在轴承振动性能可靠度降低至90%之前,应提前更换轴承或对其进行维护,安全起见,本案例中轴承应在大约5 500 min之前进行维护或更换,从而避免不必要的经济损失和人员伤亡。

3 结论

结合正反向灰自助滤波法对滚动轴承振动加速度数据进行降噪,将滤波前后数据序列的概率密度函数交集面积作为定量评定滤波效果的新指标,并与其它滤波方法进行比较从而验证正反向灰自助滤波法的效果更好。

基于泊松过程,计算轴承性能退化过程中的性能可靠度。研究结果表明:为了避免不必要的经济损失和人员伤亡,案例1中轴承应在内圈沟道磨损直径增大至0.6 mm之前维护或更换,案例2中轴承应在大约5 500 min之前进行维护或更换。