低温阀门无失效数据环节可靠性建模方法研究
卢毅, 郑建明, 赵晨
(西安理工大学 机仪学院,西安 710048)
对于现在出现的越来越多的高可靠性产品,想要获得其失效数据,不但要花费相当长的试验时间,对于那些材料昂贵或者结构复杂的产品,进行破坏性试验也是不可能的,在此情形下,更容易出现无失效数据。低温截止阀具有要求高、寿命长和价格昂贵的特点,通过试验或实际调研所获取的失效数据都集中于密封面泄露失效,对其填料环节却无失效数据可寻,从而对低温截止阀的整体可靠性评估或验收条件的制定造成困扰。
无失效数据情形常出现在可靠性试验的定时截尾试验中,属于一种特殊情况。利用当前的无失效数据可靠性评估方法得到可接受的产品寿命分布的相关参数点估计并不难[1-3]。若要得到寿命分布的真值就变得十分困难,为了提高可靠性评估的效果而引入参数的区间估计是十分必要的。
对于无失效数据条件下如低温阀门等机械产品进行可靠性评估,经国内外大量学者研究其寿命分布服从威布尔分布[4-5]。无失效数据情况下,在低温阀门的寿命分布参数估计中,bayes方法因其能够充分利用产品的先验信息,可以更好的提高其可靠性评估的精度而得到广泛应用[6-7]。茆诗松等[8]通过E-bayes的方法将产品的各个截尾时间处的失效概率配处一条产品寿命分布曲线,再得到产品可靠度的点估计;Han等[9]在指数分布条件下,利用bayes法和多层bayes法估计出各个截尾时间的失效概率,进而得到无失效数据情况下可靠度的估计;刘海涛等[10]在威布尔分布条件下,利用分布函数自身凹凸性的特点,结合bayes方法得到产品的可靠性参数估计;韩明等[11-12]将beta分布作为先验分布,在bayes基础上,提出了E-bayes和多层bayes方法的求解过程;蔡国梁等[13]通过控制样本量的变化,对比分析了多层bayes和E-bayes两种方法,结果表明:在样本量足够大时,两种方法的结果极为接近;傅惠民等[14]在威布尔分布的条件下,假设形状参数已知,得出产品寿命可靠度的置信下限;Han等[15-17]在不同的寿命分布类型中,提出了最优置信限方法,并得出可靠度的单侧置信限;贾祥等[18]通过改进配分布曲线法,提高了可靠性评估结果的可靠性;罗巍等[19]运用bootstrap方法在无失效数据的可靠性分析中,得出可靠性函数的区间估计;李东兵等[20]考虑失效率的先验分布为Gamma分布,在失效率的超参数均服从一定的均匀分布时,提出了失效率的多层Bayes和期望Bayes(Expected Bayes,E-Bayes)估计方法,建立了失效率的多层Bayes和E-Bayes估计模型;结合某型装备发动机的无失效储存数据,计算了失效率的多层Bayes和E-Bayes估计值,推导了可靠度的多层Bayes和E-Bayes估计值。
综上所述,对无失效数据情形下的可靠度估计问题,现有的研究大多只能得到参数的点估计,或者只能得到参数的单置信区间,很难同时得到参数的点估计和置信区间估计。本文结合实验,利用多层bayes方法确定取值上限参数c的值,得到各个截尾时间处的产品失效概率估计,并得到低温阀门填料环节可靠度的点估计。引入bootstrap法从已经得到的产品寿命概率分布曲线中重新抽取样本,运用矩法得出低温阀门可靠度的置信区间估计,与置信限法得到的区间对比分析得出,bootstrap法抽样法得到的区间优于置信限法。
1 低温阀门的寿命分布模型
虽然低温阀门的应用广泛,运行工况特殊,但其也是机械产品的一种,根据文献[21]可知,其寿命分布的概率密度曲线既不符合指数分布的概率密度呈现函单调递减的趋势,也与正态分布和对数分布呈现单个凸起的规律不相符,所以低温截止阀的可靠性模型符合Weibull分布,其可靠度函数为
(1)
式中:m为形状参数;γ为位置参数;η为尺度参数。
式(1)所示的Weibull分布中位置参数γ决定的是分布曲线的位置,当位置参数γ为0时代表从t=0时刻对失效状态进行描述,一般引入位置参数不仅对结果的精度影响很小,而且会使求解过程复杂许多。因此将三参数Weibull分布可简化为二参数Weibull分布,即
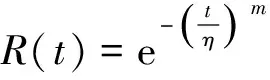
(2)
则其累计失效概率为
F(t)=1-R(t)
(3)
2 基于多层Bayes的可靠度模型建立
2.1 失效概率的多层bayes估计
失效概率pi的估计精度对产品的可靠度模型精度具有决定性的作用。目前关于无失效数据pi的估计主要方法包括经典法、Bayes法、多层Bayes法等。经典法和Bayes法都存在参数精度较差的问题。经过大量学者的研究认为,选取共轭先验分布不仅可以使计算过程简单方便,而且能提高后验分布的精度。所以本文选取与二项分布共轭的Beta分布作为pi的先验分布,其密度函数为
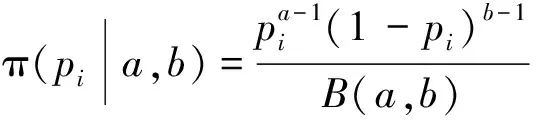
(4)
式中:a,b分别为Beta分布的未知参数;B(a,b)为Beta函数,表示为

(5)
在确定先验分布后就需要利用主观信息对先验分布进行参数区间的确定。由于机械产品在使用过程中随着时间的增加,失效率应该成递减的趋势。因此需要估算出使π(pi|a,b)递减的a、b的值。对式(4)求导可得:当0
(6)
式中c为参数b的取值上限。
多层Bayes将参数a,b视为超参数,需要对a,b进行两次积分,即需要使用两次Bayes定理,根据式(4)可知,pi的多层先验密度函数为
(7)
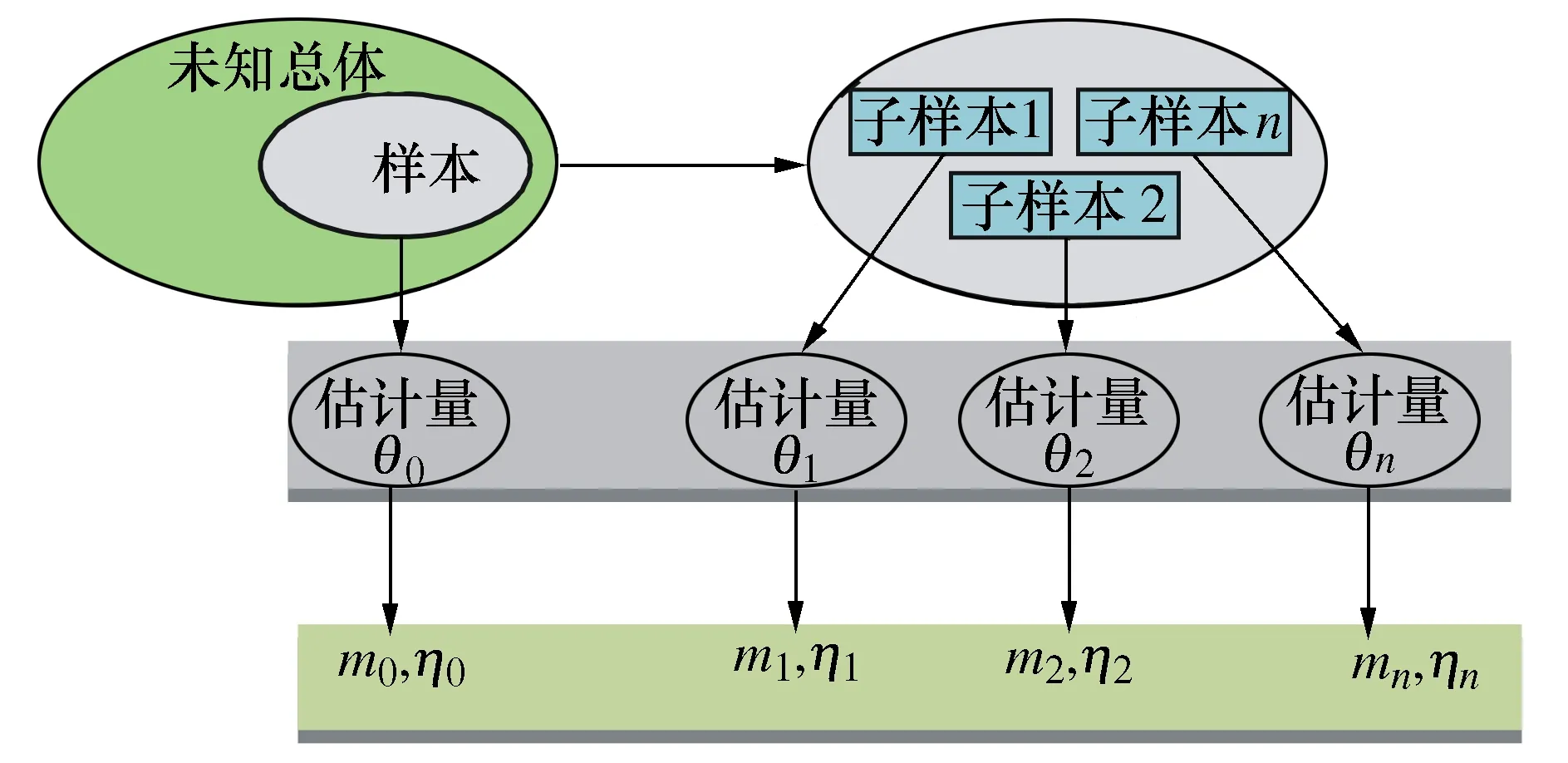
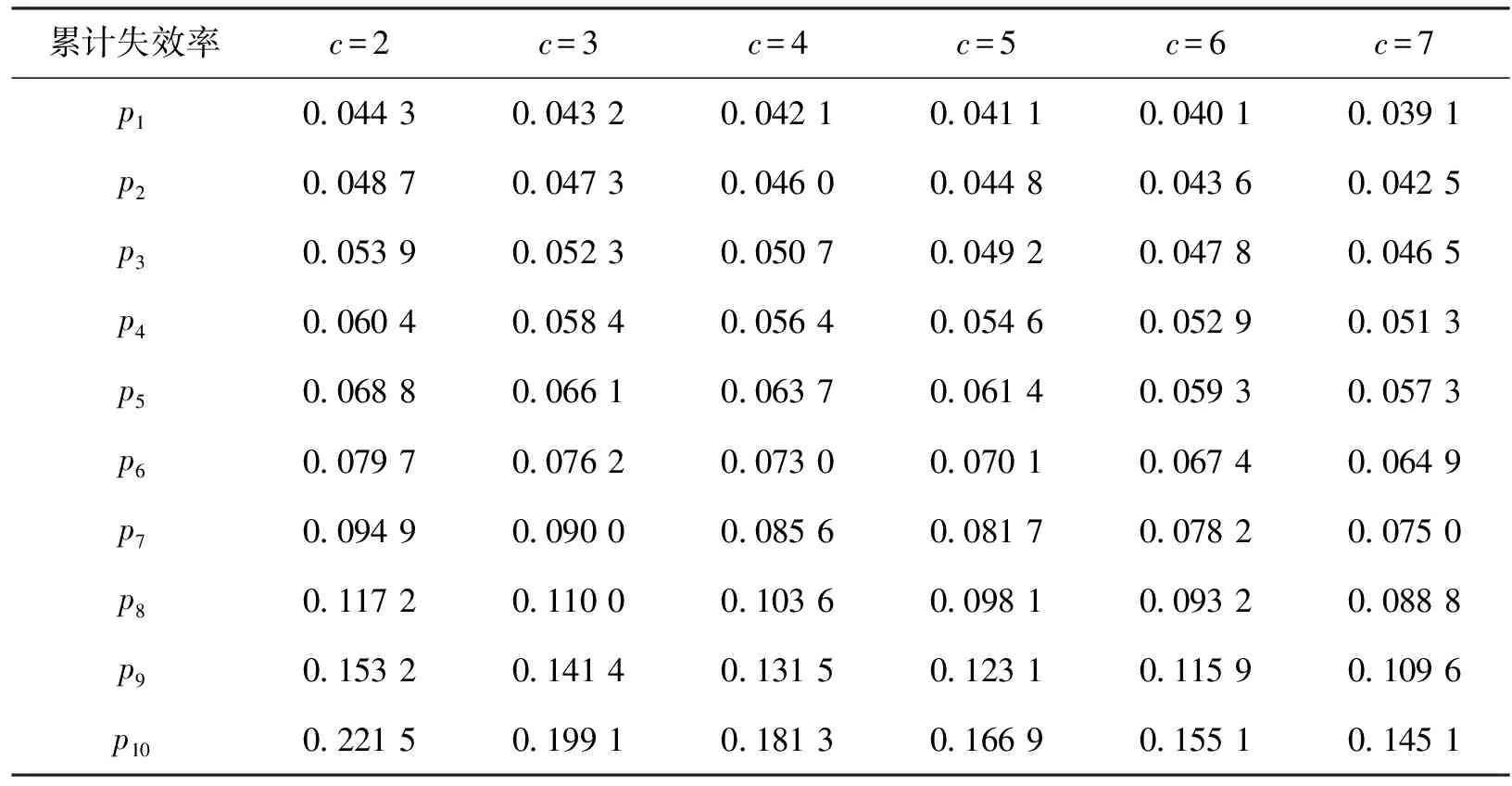
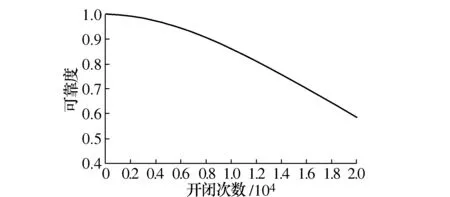
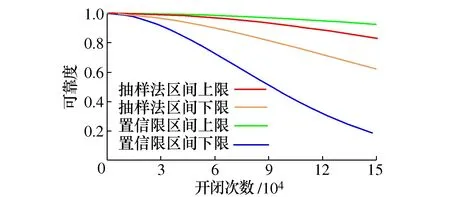
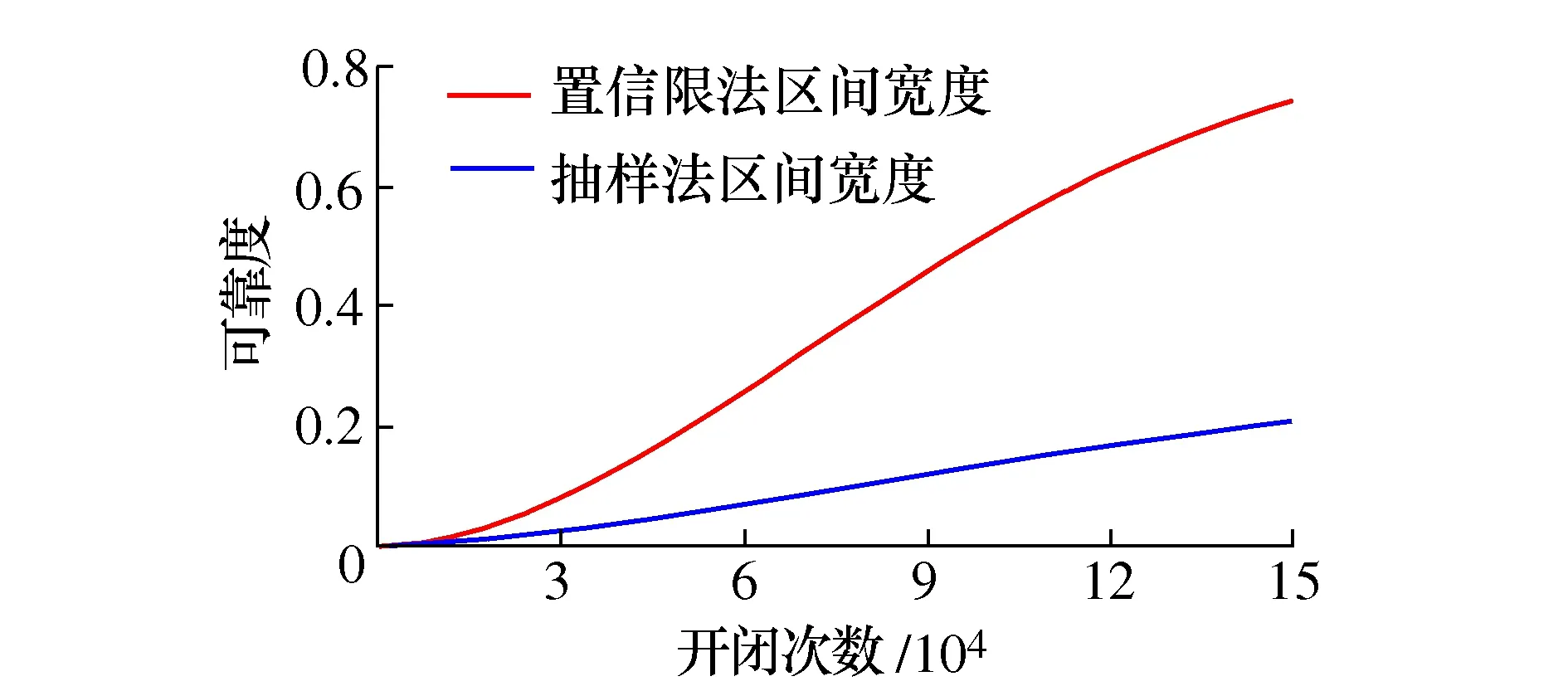
其中0 (8) (9) 对式(9)左右两边取对数可得 (10) yi=u+σxi+δi (11) 根据加权最小二乘法原理使误差δi的平方和最小求解σ和u的估计值分别为: (12) (13) (14) (15) 对于本文利用多层Bayes法所计算的结果受可靠性试验因素和求解方法的限制,只是该环节可靠度的近似模型,并不精确。因此有必要在完成点估计的基础上对建立的可靠度模型的置信区间进行研究。利用Bootstrap抽样法完成可靠度置信区间的估计,并对比不同可靠度区间评估方法的优劣性,确定低温截止阀的区间估计方法。Bootstrap抽样理论是一类虚拟增广样本计算方法[22-23],如图1所示。 图1 Bootstrap抽样原理示意图Fig.1 Schematic diagram of bootstrap sampling principles (16) 运用上述步骤需要注意的是: 1) 抽样所得的样本在进行累计失效率计算时,不能再使用多层Bayes方法,一般应采取统计理论对参数进行估计,根据文献[24]得到其分布函数估计为: (17) (18) (19) 结合现有试验条件,参照GJB899A-2009《可靠性鉴定和验收试验》与GB/T 24925-2016《低温阀门技术条件》的相关要求,对低温阀门进行低温密封性能试验与常温加压试验。 对于试验样品要满足随机抽样的原则,并根据相关标准对所抽取的样品进行强度检验和密封检验,检验合格后方可进入到低温阀门可靠性试验当中。运用阀门寿命试验台,对阀门进行常温加压试验,根据DN65低温截止阀的工况性能,试验压力为其许用压力的1.5倍。设定角度为从完全开启到达到密封扭矩所需要阀杆回转的角度,为2 160°,设定次数为阀杆启闭循环的次数,为4 100次。由于阀门开启或关闭速度不宜过快,则选取速度参数为40 °/s,并且为了防止意外造成扭矩过大的现象需要设定安全扭矩为999 Nm,一旦出现扭矩大于安全扭矩,则试验自动停止。具体试验过程如图2所示。 图2 阀门启闭与加压试验台Fig.2 Valve opening and closing and pressurization test bed 试验过程中首先将阀门通过卡盘安装在加压试验台上,连接好相应的液压系统与气路系统,最后启动启闭装置,使其通过卡具实现对阀门的开启与关闭。试验数据分为10组,其中两个试验样品为一组进行可靠性试验。根据密封填料寿命在开闭3 500次的可靠度须达到98%以上的指标要求,选取截尾次数为2 750~4 100次。而根据低温阀门启闭试验台的性能,试验开启和关闭一次大约需要1 min,每天不间断运行7 h,那么开闭4 100次则大约需要运行10 d。试验过程中,对试验样品的工作性能进行检查。试验完成后发现试验期间试验样品的密封面存在部分泄露失效,而填料环节及其他环节均与预期一致均未发生失效。 根据低温阀门可靠性试验方案步骤,当阀门在常温密封试验无失效时,则对阀门进行在低温工况下的泄露试验。该试验系统主要由气源、控制加压系统、真空系统、检测系统以及保温箱组成。其中为了将低温截止阀阀体温度保持在-163 ℃以下,采用液氮作为冷却介质模拟工况温度,如图3所示。 图3 低温性能测试系统原理Fig.3 Principles of low-temperature performance test system 低温实验用液氮作为冷却介质,用浸渍的方法达到低温试验环境,运用加压系统控制压力,提供实验所需压力,控制及检测系统用来设置试验参数,实验时,向低温试验槽中加入足量液氮,保证液氮盖住阀体与阀盖,对阀门进行降温,在阀门冷却至试验温度后,对阀门慢慢施加压力,直至达到其许用压力的1.5倍即7.5 MPa,保持30 min。待温度变化稳定在±5 ℃后,观察阀门是否泄露。 经过常温与低温密封试验以后,得出低温阀门填料环节无失效试验数据如表1所示。 表1 低温截止阀填料环节无失效试验数据Tab.1 Test data of low-temperature stop valve filling failur 通过上述对多层Bayes理论的分析与建模可知,在确定产品的似然函数与先验分布后要对可靠度参数进行求解,就首先需要对先验分布中的c值进行确定,从而得到满足产品可靠性指标要求的c值。 相关文献普遍认为,先验分布中参数b的取值会影响Beta函数的尾部取值范围,b的取值越大则导致Bayes估计的结果稳健性越差。因此b的上限值c不能过大,一般认为取2~7为宜。根据式(8)对试验所得的无失效数据c在取2~7的范围内进行计算处理,得到多层Bayes下各启闭次数的失效概率估计值如表2所示。 表2 不同c值下的多层Bayes累计失效率Tab.2 Cumulative failure rate of multilayer Bayes under different C values 由表2中的计算结果可知,填料环节在启闭3 500次的累计失效概率在c值取2~7时的失效区间为[0.064 9,0.079 7]。而根据低温截止阀的填料的指标要求,其在开闭3 500次左右的最大故障概率为pl=0.01至pu=0.02之间,显然与实际的低温截止阀的失效情况不相符。这说明按常规方法选取c值并不合适. 图4 多层Bayes下参数c与p6的关系Fig.4 The relationship between c and p6 parameters under the multilayer Bayes 结合图4可知,在满足第6次截尾时件时的累计失效概率不高于0.020的指标要求,其上限参数c的取值在多层Bayes的条件下分别为c=92。但根据Bayes估计时在参数c的值在取[2,7]时才具有良好的稳健性,因此必须对上述计算的c值进行稳健性分析。 关于c值的稳健性分析,以c值附近区间的累计失效率的极差进行度量,极差越小其稳健性越好。则根据式(8)分别求解c1±2与c2±2区间内的多层Bayes累计失效率如表3所示。 表3 多层Bayes下各截尾时刻的累计失效率Tab.3 Cumulative failure rate of each truncated time under the multi-layer Bayes 从表3可知,多层Bayes下的极差分别为0.001 0。参考相关文献极值在0.002 3附近时就代表已经有良好的稳健性,说明多层Bayes的取值都能满足Bayes估计的稳健性要求。综上,将采用多层Bayes估计取c=92对可靠度模型的未知参数进行求解分析。 (20) 因此填料环节的可靠度模型为 (21) 则低温截止阀填料环节可靠度随启闭次数变化规律如图5所示。 图5 可靠度随启闭次数变化规律Fig.5 Variation of reliability with opening and closing times 从图5中可以看出,使用多层Bayes点估计的可靠度呈单调递减的趋势,在开启次数4 000次左右,可靠度保持90%以上,随着开启次数不断增大,其可靠度减小速度增大。 根据Bootstrap抽样法求解流程,将上述所得的累计分布曲线作为总体的分布曲线对样本进行抽样。首先为了清楚的观察抽样次数B对参数估计效果的影响,在不同抽样次数时估计可靠度区间随抽样次数B的波动情况,当可靠度区间稳定时则说明B已经满足要求。其中新抽取的样本数量需与原始样本的数量保持一致,即n=20。本文选择抽样次数为0~4 000次,可得置信度为90%时可靠度区间宽度的变化情况如图6所示。 图6 Bootstrap抽样次数与区间波动关系Fig.6 Relationship between bootstrap sampling times and interval fluctuation 从图6可以看出在抽样次数在1 000次以内时,可靠度区间的上下限存在明显的波动。抽样次数在1 000~2 000次之间时,区间上下限的波动逐渐减小。当抽样次数在2 000次以上时,区间上下限基本趋于收敛。为了得到精确的可靠性评估区间,确定采取抽样次数B=2 500次。 采用上述确定的参数并利用MATLAB同时可以得到填料环节可靠度的区间估计随开启次数关系表达式和变化规律为 (22) 将式(22)得到的区间估计与多层Bayes得出的点估计进行对比,如图7所示。 图7 可靠度随启闭次数变化规律Fig.7 Variation law of reliability with opening and closing times 从图7中可以看出,随着开闭次数的增加,该环节的可靠度呈单调递减的趋势,其中在开闭次数较短时,使用多层Bayes的点估计包含于Bootstrap的区间估计之中且区间的宽度很小,即误差较小。随着阀门开闭次数的不断延长,可靠度的区间虽始终包含多层Bayes的点估计值,但区间宽度却明显变大。而造成这种问题的主要原因是可靠性试验中试验样本的数量过少所导致的,因为样本量越大则区间估计的越窄,点估计的值越准确,但该现象区间求解方法是无关的。综上,采用该方法能完全满足低温截止阀无失效数据环节的可靠性评估。 由于产品的无失效数据很难计算产品可靠度参数的真值,因此本文引入置信限法求解参数的置信区间,并通过对比置信限法与Bootstrap法所计算的可靠度区间结果的精度,确定适合填料环节的置信区间求解方法。傅惠民对寿命服从weibull分布条件的产品进行了研究,在形状参数确定的条件下,推导出尺度参数双侧置信区间的估计方法,得到可靠度区间估计。根据文献[17,26-27]可得置信限法尺度参数η的估计区间上限和下限为: (23) 根据可靠度的点估计公式,将式(23)代入式(15)可得置信水平在1-α下可靠度估计的区间上限和下限为: (24) 同样选取置信限法的置信水平与Bootstrap抽样法的置信水平相同,即取90%的置信度进行计算。两种区间估计方法的可靠度区间随开闭次数的变化规律如图8所示。并且为了研究不同区间估计方法下的区间宽度变化情况,令D=|Ru(t)-Rl(t)|,因此可得两种方法下的区间宽度如图9所示。 图8 不同模型下的可靠度区间估计Fig.8 Interval estimation of reliability under different models 图9 不同模型可靠度区间宽度的变化规律Fig.9 Variation of reliability interval width of different models 从图8可以分析得到Bootstrap抽样法的区间宽度明显优于置信限法,在开闭次数较大时,置信限估计法便失去了统计意义。同时从图9中可知,在开闭次数小于1 000次时,置信限法与Bootstrap抽样法的区间宽度均保持一致,且区间宽度小于0.05。但随着开闭次数的增加,置信限法的区间宽度为0.8明显大于Bootstrap抽样法的0.2。所以证明采用Bootstrap抽样法对填料环节置信区间的估计是比较准确的。 本文结合实验,利用多层bayes方法得到各个截尾时间处的产品失效概率估计,并得到低温阀门可靠度的点估计;并引入bootstrap法从已经得到的产品寿命概率分布曲线中重新抽取样本,结合矩法得出低温阀门可靠度的置信区间估计,最终与置信限法得到的区间进行对比分析,结论如下: 1) 分析了多层Bayes方法中先验分布中参数c值的选取,结合填料相关指标信息,给出了低温截止阀填料中参数c确定值。通过分析多层Bayes下c对应取值的稳健性,选取多层Bayes对失效率进行估计,获得了填料环节的可靠度模型。 2) 在无失效数据情况下,通过对低温截止阀的填料环节进行可靠性分析可知,通过多层bayes方法得出低温阀门填料环节的可靠度点估计,运用Bootstrap抽样法和矩法的结合得出填料环节可靠度的区间估计,使填料环节的可靠性评估更加精确。 3) 采用Bootstrap抽样法对可靠度曲线进行了多次抽样,并根据样本获得了填料环节可靠度的置信区间。通过与置信限法的参数区间估计法进行对比,确定该方法在填料环节的无失效数据可靠性处理上其精度明显高于置信限法,满足无失效环节可靠性评估的相关要求。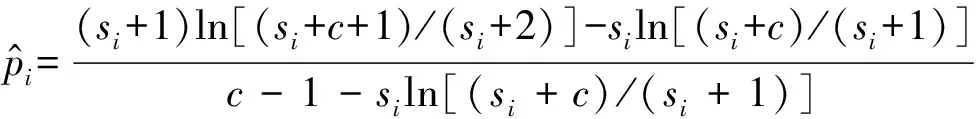
2.2 可靠度的点估计
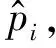
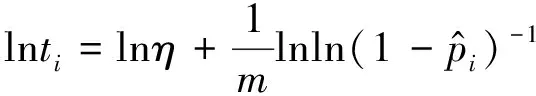
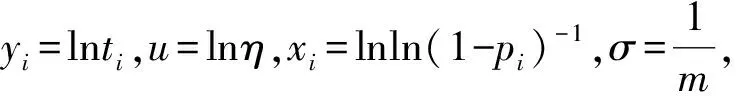

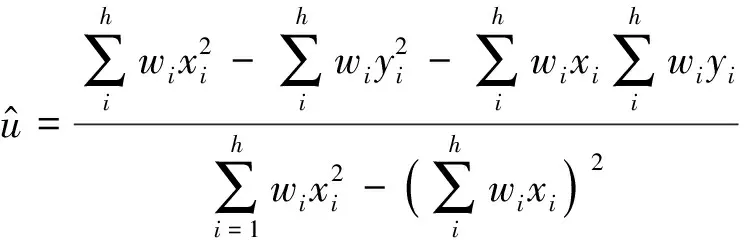
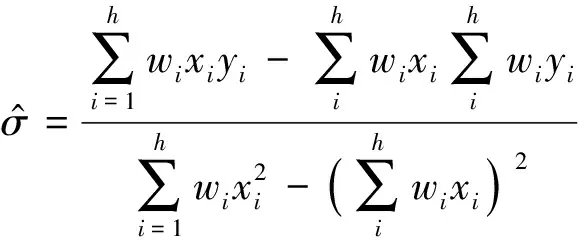
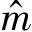
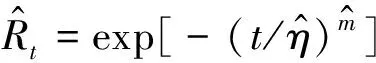
3 可靠度的置信区间估计
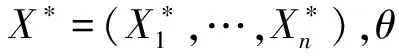
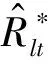
4 低温截止阀无失效环节数据分析
4.1 低温阀门的无失效实验数据样本


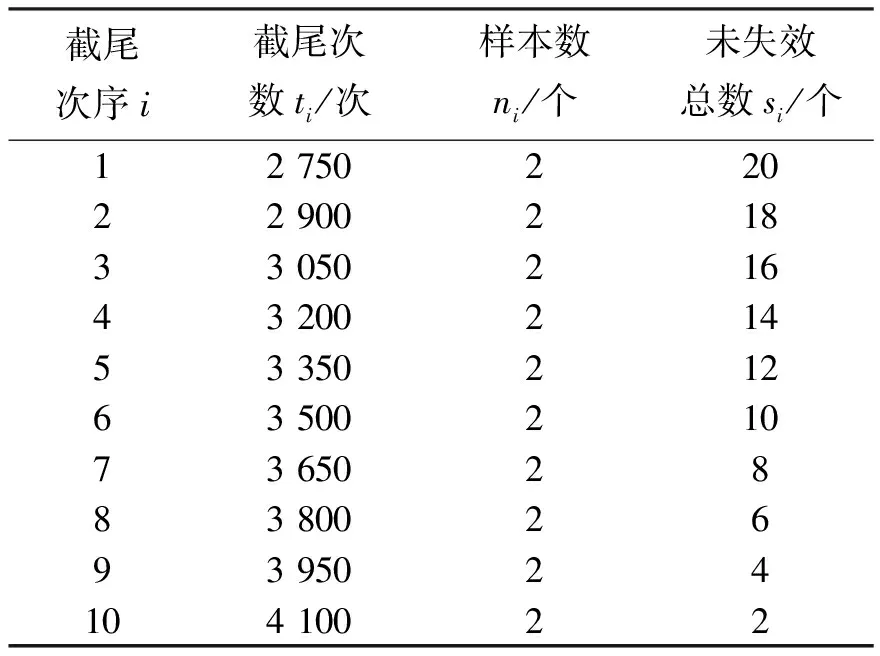
4.2 多层Bayes法取值上限参数c值及可靠度模型参数的确定
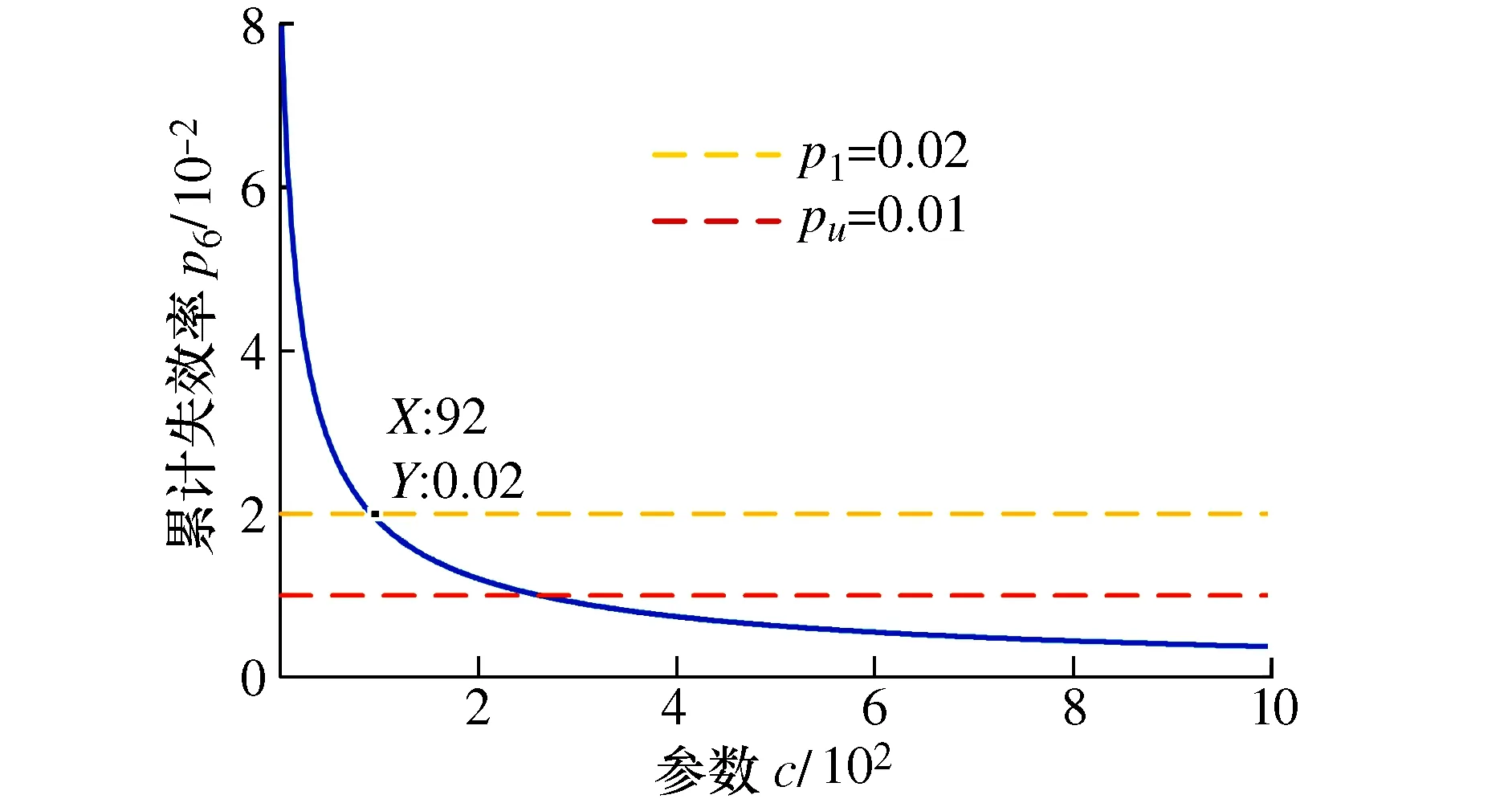
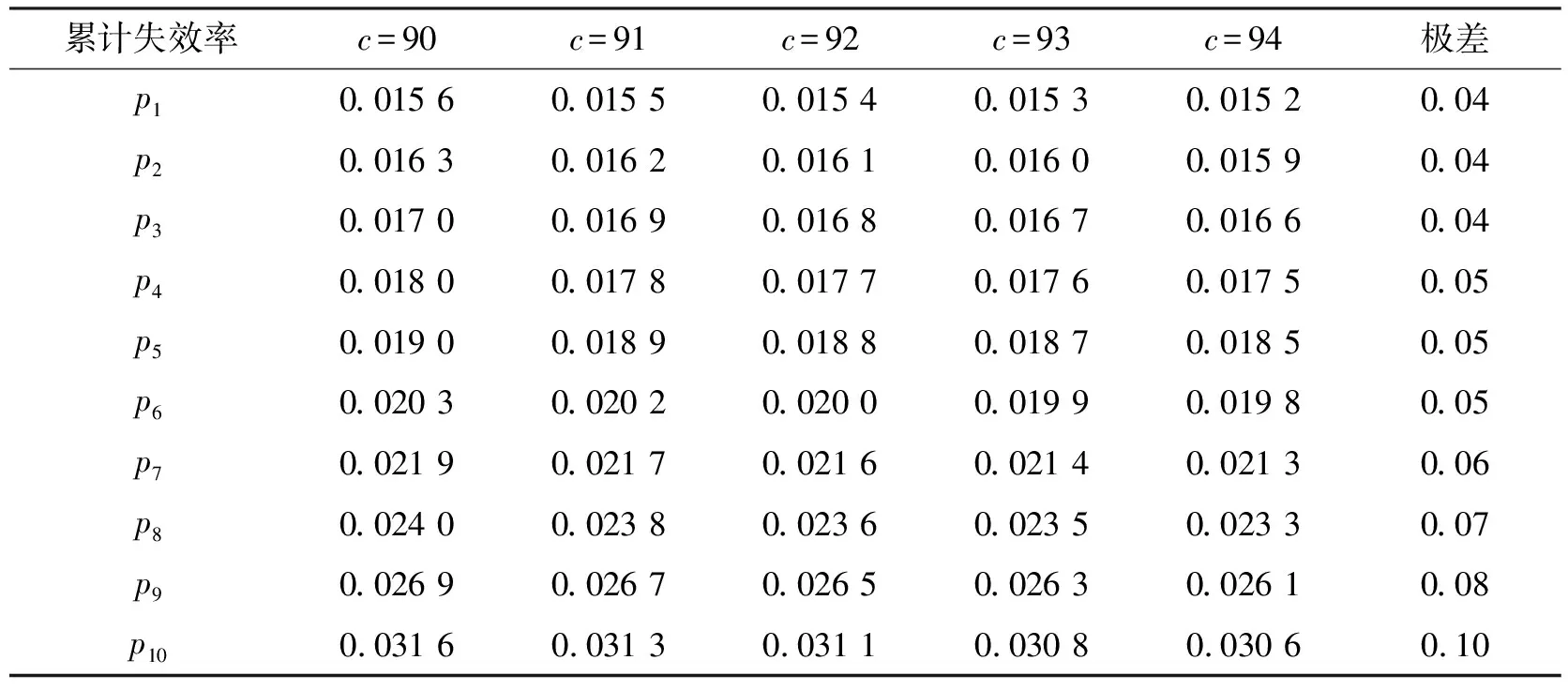
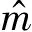
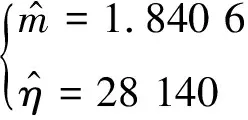
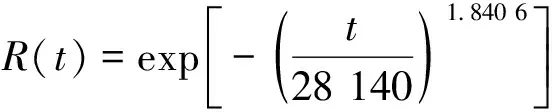
4.3 Bootstrap抽样法与置信限法可靠度置信区间对比

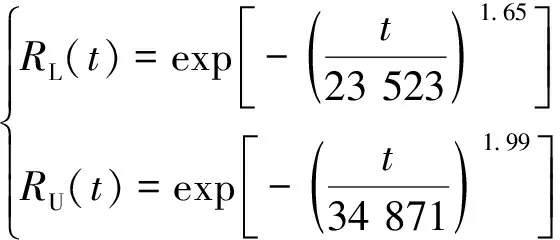

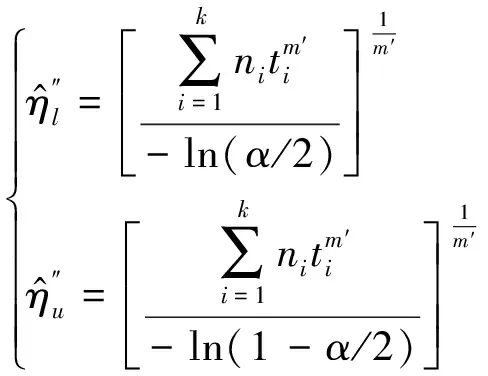
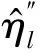
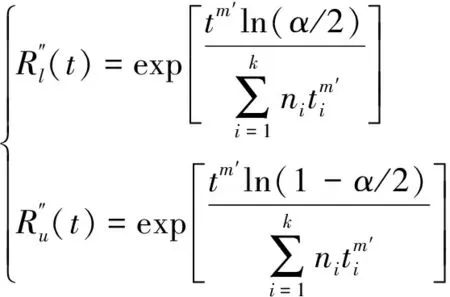
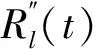
5 结论

