基于数据融合的不平衡连续手术动作分割识别
郑嘉颖, 王杰, 付攀, 李桢, 边桂彬*
(1.北京信息科技大学自动化学院, 北京 100096; 2.中科院自动化研究所, 北京 100190)
基于可穿戴传感器的动作识别是目前研究人类行为及操作的重要部分,可以应用于医疗保健、娱乐等多个领域中,目的在于识别出一段数据序列中的动作或操作构成,以方便后续的分析及研究。当前的有关利用可穿戴传感器数据的行为识别领域,需要分析的动作序列通常被拆解成单个动作进行识别,而真实情境下完成一个复杂的操作时通常需要连续完成多个动作,在连续的自然动作中,很难精密地控制每一个动作出现的频率和持续的时间长度,因此采集到的数据总体长度不一致的同时也很容易出现样本数据分布不平衡的问题。针对样本不平衡的研究由来已久,例如在疾病诊断领域[1]以及故障诊断[2]领域,往往是正例多于负例,极端情况下可能会出现负例全部被判断为正例,然而正确率依然很高的情况,这并不符合人们的期待。针对不平衡数据的问题,对数据集重采样[3]或者进行数据增强[4]是常见的处理方法,即通过修正数据集中的样本分布使其均衡,从而避免数据分布差异大引发少类数据的识别精度低于多类数据。但是重采样并不适用于所有的情况,降采样会丢失有效信息,过采样则会加重过拟合现象。另一种改进方法是通过为损失函数增加权重,增加少数类数据判断错误时的损失,如使用Focal Loss[5]或增加权重的交叉熵损失函数[6],但这两种需要使用权重的损失函数需要花费较多精力调整权重参数,为训练带来了不小的负担。
非平衡问题的出现,本质是因为少类数据中含有的信息量不及多类数据中含有的信息量丰富易得,因此在同样的训练进程中很难获得相同的学习效果。近年来的研究结果证明,数据融合的方式可以有效提高识别的准确度与可靠性[7],因此现引入数据融合算法以提升少数类数据的特征提取效果。数据融合或多传感器融合算法最早应用于军事领域,但近年来由于传感器技术的改进,该技术也被应用于导航、医疗等领域。如汽车自动行驶中各部分传感器采集数据,实时融合并获得分类或预测结果,以保障汽车在自动驾驶中的安全[8],医疗中则常用于各类穿戴设备辅助检查疾病[9],研究证实,特征融合可以提高网络的特征表达能力,如可以将行人识别任务中来自不同模块的特征进行优势互补,提升行人识别的效果[10]。
简单的数据融合算法可以将从不同数据中提取的特征进行简单的搭配,如特征拼接或特征相加等,除了这种基本融合方法外,还有以加权融合为核心的算法。Zadeh等[11]考虑充分利用各个模态中的特征,提出了一种矩阵融合策略张量融合网络(tensor fusion network,TFN),该算法首先对每个模态进行维数扩展,并对不同模态求笛卡尔乘积,其缺点是融合的维数过高,会产生较多的冗余信息,需要消耗较多的内存。Liu等[12]针对上述缺点提出了基于低秩因子分解原理的多模态数据融合策略低秩权重融合(low-rank weight fusion,LWF)。LWF将常规全连接层中的权重矩阵分解为几个维数较低的矩阵,即低秩因子,并使用低秩因子对各模态的特征矩阵进行运算,然后找到所有模态数据的点积。该融合策略充分降低了运算的复杂性,但特征长度过长时仍然会出现参数爆炸的情况。随着注意力机制的开发与应用,近年来不断有研究将注意力机制引入数据融合算法,如用于多模态情感识别[13]、行为识别[14], 语音识别[15]等领域中。自注意力和跨模态注意力通过捕捉样本的全局特征并筛选出特征中真正重要的部分从而完成特征的有效融合。
综上所述,针对连续动作的不平衡数据分类与识别问题,现设计一种基于数据融合算法的手术动作识别及分割算法。在验证阶段,因手术中的动作复杂而精细,很适合采集连续的动作数据用于验证模型的效果,利用多种可穿戴的传感器采集眼科医生进行白内障撕囊操作的动作数据,建立连续手术操作多模态数据集。利用数据采集实验中采集的连续手术动作数据对该模型进行模型效果对比验证,证明该模型能够处理小样本情境下不平衡连续时间序列数据的分割与识别问题。
1 多模态连续手术动作的识别与分割算法
所提出的基于数据融合的连续动作分割识别模型总体结构如图1所示。该模型可分为深层特征提取模块、特征融合模块和解码器网络3个部分,特征提取部分基于双向长短时记忆网络(bidirectional long short-term memory networks, Bi-LSTM)构建。长短时记忆网络(long short-term memory networks, LSTM)属于循环神经网络,是处理时间序列数据的常用算法,能够提取时间序列的时域特征,相关研究证明Bi-LSTM在人体活动识别任务中的分类效果优于LSTM[16]。因此使用Bi-LSTM作为基础,并且利用网络的多层堆叠技术充分扩充了网络容量以提升数据特征的提取效果。各模态数据输入特征提取模块后获得单模态特征,随后两两配对输入特征融合部分,获得双模态融合特征后与单模态特征拼接,输入自注意力机制模块获得最终融合特征,解码器模块对最终融合特征进行解码,将特征序列映射为动作序列作为模型输出。

A、B和C表示不同模态的输入数据
1.1 深层动作数据特征提取
为保证模型能够提取深层次的数据特征将原始数据输入堆叠的长短时记忆模块,该模块包含3层Bi-LSTM与1个残差LSTM,残差LSTM的结构如图2所示,经过Bi-LSTM后的输出数据与输入数据拼接,作为下一层的输入,单层Bi-LSTM的计算公式与LSTM相同,但会将序列反向输入再次进行计算,最后的输出是正向输入的输出与反相输入的输出的拼接,LSTM计算公式如式(1)~式(6)所示。
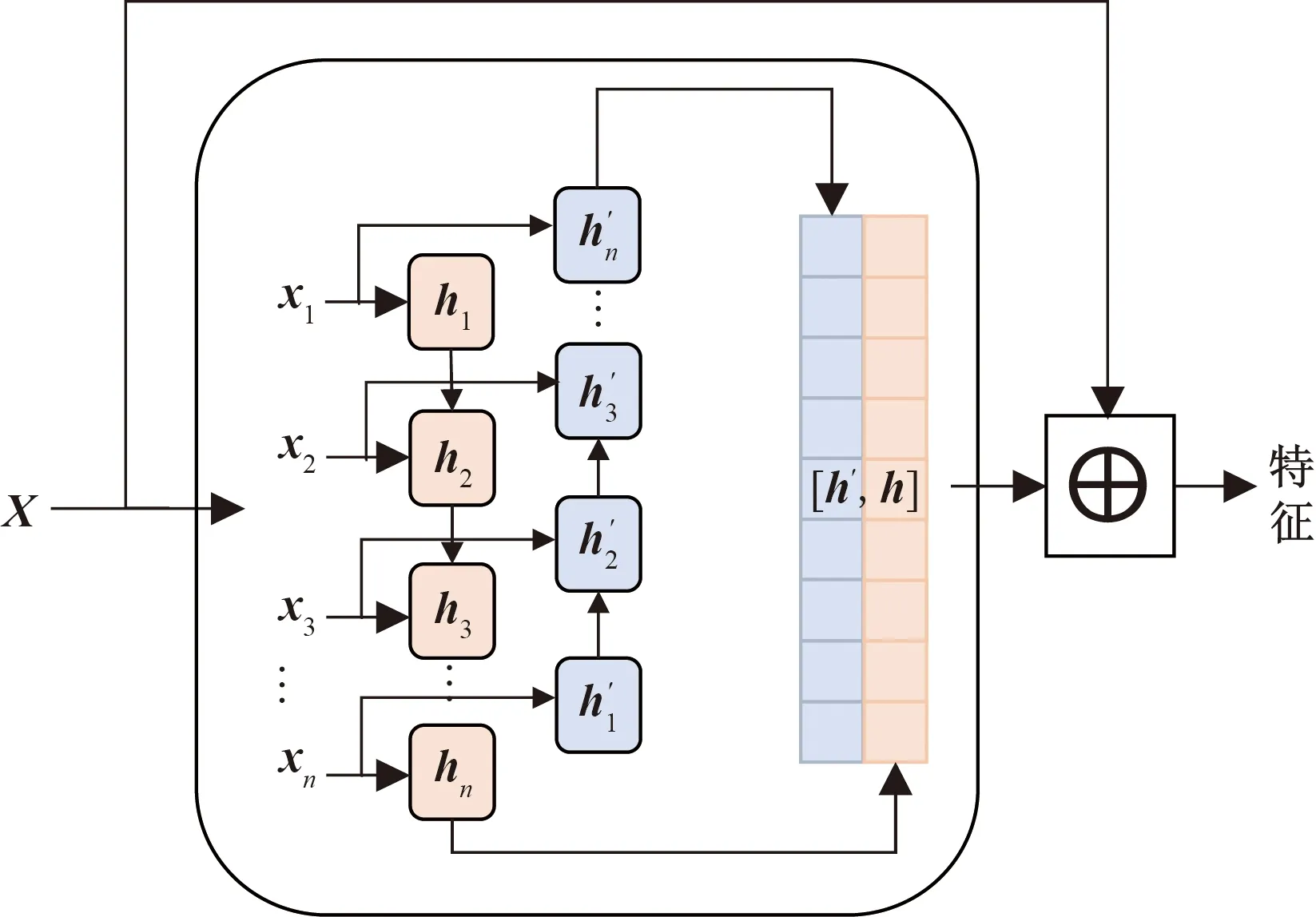
图2 残差LSTM模块结构Fig.2 Residual LSTM module structure

(1)
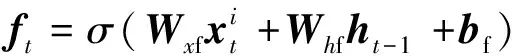
(2)
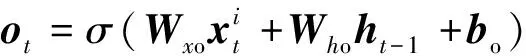
(3)

(4)

(5)
ht=ot⊗tanhct
(6)
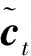
1.2 双模态特征融合模块
双模态特征融合模块结构如图3所示。交互注意力机制用于融合双模态特征,记模态α和模态β的特征分别为Zα∈RL×dα,Zβ∈RL∓×dβ。其中,由于在数据处理过程中对齐了各模态的数据,各模态的时间长度均为L,dα和dβ分别为两个模态的特征对应的维度。该模块使用模态α计算查询矩阵(Query),记为Qα,使用模态β计算键矩阵(Key),记为Kβ通过模态α和模态β的联合计算值矩阵(Value),记为Vαβ。

图3 双模态特征融合模块Fig.3 Bimodal feature fusion module
Qα=ZαWQ
(7)
Kβ=ZβWK
(8)
Vαβ=[Zα,Zβ]WV
(9)
式中:WQ∈Rdα×dq、WK∈Rdβ×dk、WV∈R(dα+dβ)×dv为线性变换的权重矩阵;dq、dk和dv分别为线性变化后的输出维度,其中dk=dq=d。模态α和模态β的交互注意力可以使用式(10)计算。
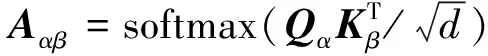
(10)
式(10)中:Aαβ为注意力分数矩阵。
最后将Value与使用注意力分数加权后的Value相加,经过层归一化(LayerNorm)后得到跨模态特征Yαβ,计算过程如式(11)所示。
Yαβ=LayerNorm(Vαβ+AαβVαβ)
(11)
数据经过两两组合输入双模态特征融合模块,得到3组初步融合后的特征,在最后的融合阶段,还需要将各个模态单独的特征向量与这3组双初步融合进行拼接,并输入自注意力[17]计算模块进行最后的融合计算。
1.3 解码器
经过提取多模态特征并融合之后,需要对特征进行解码获得最终的输出。如图4所示,解码器模块则由三层全连接层完成动作特征到动作标签的映射,采用的激活函数为线性整流单元(ReLU),并插入丢弃正则化层(Dropout)以防止过拟合。

图4 解码器模块结构图Fig.4 Decoder module structure
2 连续动作分割识别实验
2.1 数据采集与预处理
2.1.1 数据采集
为收集到能够完整反映手术操作的动作数据,选择光纤弯曲传感器、光学定位系统和压力传感器等3种传感器,分别收集医生操作时的手指关节和手腕的活动、手部运动以及医生手部与手术器械间的交互力。
数据收集实验模拟真实的外科手术设计,以生理指标与人类较为相似的新鲜离体猪眼球作为数据收集模拟实验的材料。数据采集如图5所示,新鲜的离体猪眼球通过离体猪眼球固定基座固定在手术台上,并与经过校准空间坐标的光学定位传感器保持相对固定,3枚光学标记点,6枚光纤弯曲传感器和2枚迷你型压力传感器分别安置在右手拇指、食指指尖、腕关节处,拇指、食指的近掌关节、指节关节和腕关节活动处,拇指、食指夹持手术器械的接触点处,光纤弯曲传感器安装时需要注意轴线与手指关节轴线重合,以确保数据采集系统能收集到真实的动作数据。

图5 数据采集Fig.5 Data acquisition
仅采集连续环形撕囊术操作,操作中眼科医生右手持撕囊镊,使撕囊镊前端通过角膜缘切口进入眼球前房,用撕囊镊尖端划破晶状体前囊膜并挑起可夹取的囊瓣,这一操作通常被称为起瓣,随后使用撕囊镊尖端夹紧囊瓣并牵引囊膜沿圆形轨迹裂开,在牵引囊瓣中需要在合适的位置松开撕囊镊并变更囊瓣夹取点,以确保撕囊过程中不失去对撕囊轨迹的控制,这一行为称为换手,撕囊过程中牵引囊瓣和换手需要交替数次,直至撕囊结束后撕囊镊夹持撕下的囊瓣并退出眼内空间。数据采集实验分为4次,共计130组实验,实验中使用眼科显微镜记录了手术中的图像数据作为标记运动数据的依据,将动作数据标记为进入(I)、起瓣(MC)、换手(CP)、牵引囊瓣(T)、退出(O)共5种动作类型。最终筛选出用于验证模型的数据共计29组,为17维变长时间序列。数据的构成比例如图6所示,最大类T与最少类O之间的数量差接近10倍,为非平衡数据。

图6 数据标签比例Fig.6 Ratio of data labels
2.1.2 数据预处理
1)空间坐标转换
因数据采集实验共分4次进行,每次数据采集均需要重新校准光学定位仪的测量空间,因此每次实验中的空间坐标系不一致,需要进行空间坐标的统一。利用布尔莎空间坐标转换[式(12)和式(13)]将4次数据采集中获得的手部运动数据转换到统一的坐标系下。

(12)
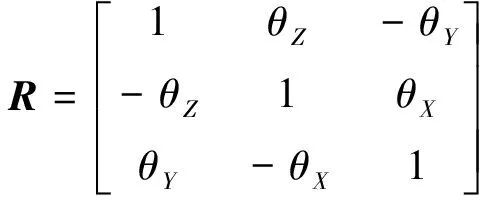
(13)
式中:(xa,ya,za)为坐标系A下某一点的三维坐标;(xb,yb,zb)为该点在坐标系B的三维坐标;(xt,yt,zt)为两个坐标系间的平移参数;θx、θy、θz分别为坐标系B转换到A时3个坐标轴的旋转角度;R为空间坐标旋转矩阵;m为坐标系转换的比例参数。
2)时间域对齐
数据采集中使用的3种传感器的采样频率接近但不一致,但是特征融合过程中必须按照时间匹配不同模态下的数据特征,因此需要建立一种时域对齐算法。光学定位传感器的采集频率为60 Hz,压力传感器的采集频率为62 Hz,光纤弯曲传感器的采集频率为64 Hz,经过时域对齐后将3种数据的采集频率统一为60 Hz,本时域算法的误差小于等于4 ms,开始时输入需要进行时域对齐的数据A与数据B各一组,数据A和数据B分别为长度为L1和L2的多维时间序列,以其中采样率更低的数据的时间戳作为时域对齐的基准,假定数据A的采样率更低,则将yti记为ti时刻的数据B,(i=0,1,…,L1)。记tj时刻的数据A为xtj,(j=0,1,…,L2)。遍历数据A的时间戳数据,计算时间戳之间的误差Δt=|ti-tj|,若Δt≤4 ms,则将xtj记录为[xtj,yti]。若4 ms<Δt≤12 ms,则记录xtj=[xtj,0.5(yti+yti±1)],若Δt>12 ms,则记录xtj=[xtj,yti±1],其中的±由ti和tj的大小决定,若ti>tj则取负号,反之则取正号。
3)归一化
为了保证数据特征的有效提取,加快训练过程中模型的收敛速度,采取标准化将原始数据规范到标准分布。标准化计算如式(14)所示。
z=(x-μ)/σ
(14)
式(14)中:z为标准值;x为原始数据;μ为平均值;σ为标准差。
2.2 模型效果验证
2.2.1 实验环境与训练策略
所提出的模型基于PyTorch平台搭建(GPU: NVIDIA TITAN XP, RAM: 4×12 G, Driver Version: 515.65.01, CUDA Version: 11.7)。训练中所有的模型中均使用Adam优化器,大小为1×10-5的L2正则化因子,dropout概率为0.2,损失函数使用交叉熵。训练中将数据集划分为训练数据集和测试数据集,超参数的选择部分使用十折交叉验证,训练数据集被划分成为10个子集,每次取9个子集用于训练模型,1个子集用于验证模型。模型对比实验中的评估指标包括分类准确度,每一类的F1分数,以及全局F1分数,全局F1分数表示模型整体的F1分数。提到的所有评估指标均由混淆矩阵计算得到。
2.2.2 基线模型与模型对比实验
选择的基线模型共计7种,其中①~③为数据层融合模型,隐藏元数量均设置为16,学习率均设置为0.001,总训练次数为150,3个模态的原始数据经过预处理及标准化后直接按照维度拼接,随后直接输入基线模型,经全连接层降维后输出分类结果;④~⑦为特征层融合模型,学习率为0.001,总训练次数为350,分为特征提取部分与特征融合部分,特征提取均由隐藏元数量为16的单层长短时记忆网络完成,融合后特征通过使用dropout策略的全连接层输出分类结果。
7种基线模型详细介绍如下:①LSTM(单层及双层);②Bi-LSTM(单层);③GRU(单层);④LSTM-CONCAT,CONCAT为拼接算子,表示经特征提取单元提取的各模态特征通过拼接获得融合后特征;⑤LSTM-ADD,ADD为带有可学习权重的加法算子,表示经特征提取单元提取的各模态特征通过求加权和获得融合后特征;⑥LSTM-TFN,TFN[11]是基于矩阵运算的特征融合算法,来自不同模态的特征矩阵的笛卡尔积作为融合后特征;⑦LSTM-LWF,LWF[12]是基于低秩矩阵分解的特征融合算法,将权重矩阵分解为低秩因子,低秩因子与特征相乘后累加获得融合后特征。
模型对比试验结果如表1及表2所示。由表1和表2中的数据可知,对比基线模型,提出的模型能够取得最高的准确率和全局F1分数,在每一类的分类中也取得了最佳的F1分数,同时对类别O的分类效果提升尤其明显,说明通过提取深度动作数据特征可以缓解样本数量少难以学习带来的分类精度不高的问题。特征融合模型由于特征提取部分完全一致,可以直观地比较融合算法的效果,带权重的加法算子优于拼接算子,LWF算法优于TFN算法。另外,由于总体数据量有限,当模型为双层堆叠的LSTM时出现了严重的过拟合现象,分类效果与单层的LSTM相比准确率下降了3%,进入(I)和退出(O)的分类F1分数下降了15%以上。说明数量有限时提升模型参数量反而会使分类效果下降,但提出的模型中使用了3层堆叠的Bi-LSTM,理论模型参数远大于基线模型,仍能取得最佳的分类成绩,充分说明了所提出的模型具备结构上的合理性。

表1 模型分类效果评估

表2 5种动作类型F1分数
2.2.3 超参数调整
为找出最适合模型的超参数组合,对学习率以及L2正则化因子两个超参数进行网格搜索,超参数搜索结果如图7与图8所示,F1分数受学习率影响较大,而准确度受超参数影响较小,学习率为0.009时,模型能取得最佳的分类准确率与F1分数。L2正则化因子为1×10-5时的准确度最高。
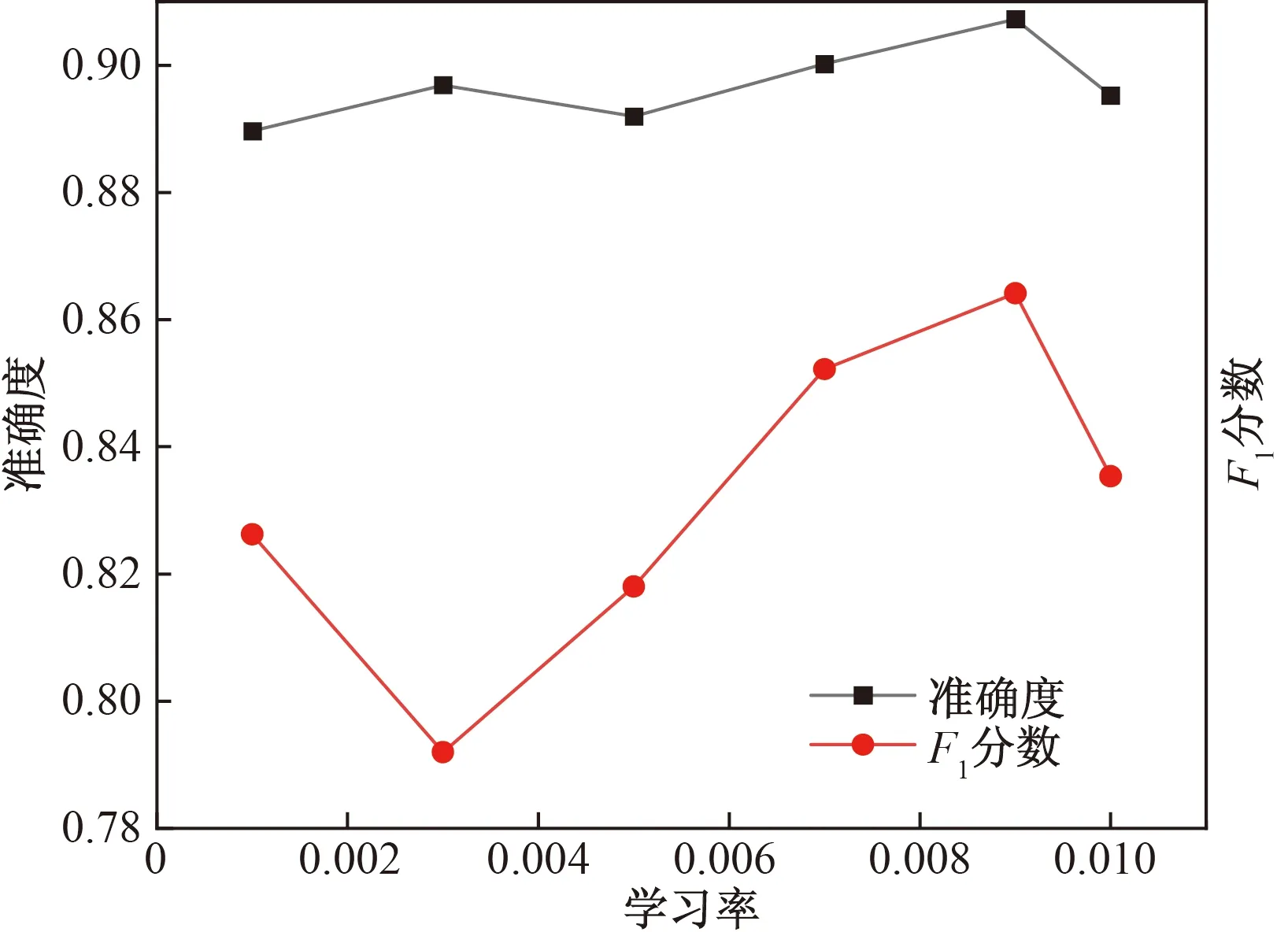
图7 学习率-分类指标曲线Fig.7 Learning rate-classification indicators curve

图8 L2正则化因子-分类指标曲线Fig.8 L2 regularization factor-classification indicators curve
2.2.4 模型输出结果可视化
对测试样例的模型输出的动作序列以及真实动作序列进行可视化对比,如图9所示,将动作标签映射为不同的色块,上侧序列为真实动作序列,下侧为模型输出的动作分类序列。对照颜色分布,所提出的模型识别出的动作序列与真实序列基本保持一致,序列中,眼科医生在此次操作中共执行了5次换手及牵引囊瓣操作,撕下囊瓣后退出眼内空间。第三次换手动作和牵引囊瓣动作以及最后一次牵引囊瓣到退出两次动作转换衔接处出现较多的判断失误,推断原因为动作转换处特征区分不大,较易误判。总体来看,提出的模型能够完成连续动作序列分割与识别任务。

图9 模型输出可视化结果Fig.9 The visualization of model’s output action sequence
2.2.5 不同损失函数下的分类效果对比
为验证提出模型使用不同损失函数时的分类效果,使用两种针对数据集不平衡开发的损失函数进行测试,测试结果如表3和表4所示,WCE能够提高模型的全局F1分数,而准确度出现轻微下降,说明带权重的损失函数确实提高了模型分类的平衡性,但不同类的F1分数却出现了较为有趣的现象,WCE和FL提高了少数类I的分类效果,但对少数类O的分类效果并不突出,其他多数类的分类效果也出现下降。
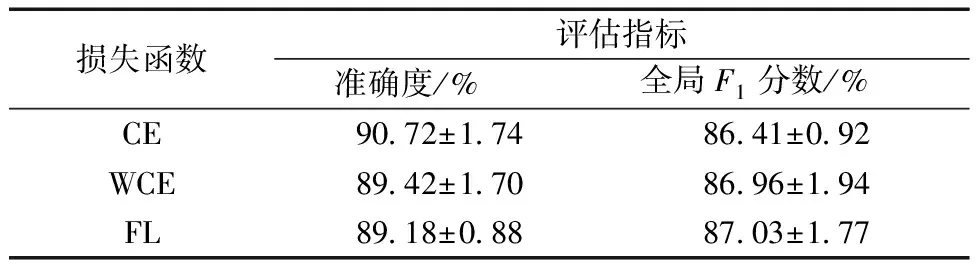
表3 3种损失函数下的分类效果

表4 3种损失函数下的5种动作类型F1分数
3 结论
针对数据集不平衡下的多分类问题与连续动作序列中的动作识别与分割问题,提出一种端到端多模态时间序列分割模型,此模型采用编码器-解码器结构,编码器用于提取数据特征并融合,解码器将融合后的特征映射到分类标签。在编码器中提出一种新的数据提取模块和一种新的双模态数据融合机制,可以有效提取多传感器数据的时域特征并进行有效的融合。同时,通过多传感器数据采集平台采集了多传感器连续环形撕囊术操作数据,利用该数据对所提出的模型进行验证,实验结果证明所提出的模型可以有效分割出连续手术操作中医生的各个动作,并且能够处理数据集标签分布不平衡情况的多分类问题,实验数据显示,所提出的模型在模型效果对比实验中取得了90.72%的准确率,优于基线模型。实验同时对比了不同损失函数下的模型分类效果,同样取得最优的分类准确率,结合可视化结果,充分证明了所提出模型的有效性。
在研究中得到以下结论。
(1)数据量较小时扩增模型参数量会导致过拟合,影响分类效果。
(2)提升特征提取的深度和粒度能够有效改善样本数量少带来的分类困难。
(3)提出的模型够有效提取并融合来自多模态数据的深度特征,有效提升分类效果。

