深部砂岩力学实验及储层开采出砂影响规律

韩忠英, 孙波, 王芸涵, 程远方, 闫传梁

(1.中国石油大学(华东)石油工程学院, 青岛 266580; 2.中国石油大学(华东)非常规油气开发教育部重点实验室, 青岛 266580)

目前中国对天然气的勘探已经不断向深层、超深层拓展[1-2]。深层、超深层气井储层温度较高、地层压力大、流体渗流机理与浅部地层差异比较大。在勘探开发过程中发现,深部储层岩石的致密性高,压实和胶结强度大,不易发生破坏,但是由于温度场、渗流场和应力场的相互作用,岩石结构破坏形式复杂,开采过程中易产生气井出砂[3-5]。

塔里木盆地克深气田是世界上罕见的深层裂缝性砂岩油气藏。近几年来克深气田的开发井均呈现不同程度的出砂现象[6-7]。特别是天然气田开发后期,储层岩石胶结强度降低,含水上升,导致开采时流体更容易携带地层砂进入井筒,使出砂程度加剧[8-11]。目前出砂问题是天然气井勘探开发的重点难题之一[12]。出砂给气井的生产产生消极影响,如:出砂会导致井下、井口设备的磨损,大大缩短设备使用寿命;中度或重度出砂可能会导致砂筒堵死,井筒积砂积液,更严重的还会导致长关井[13-14]。

近些年来国内许多外专家、学者对油气藏的出砂机理和出砂规律都进行了大量的研究工作[15],张文斌等[16]根据储层岩石的特性和生产的条件,分析疏松地层气井出砂的原因和机理,制定合理的生产方式,从而有效控制出砂;李春云等[17]针对春光油田沙湾组地层的结构特点,考虑到该储层岩石胶结强度比较低、容易出砂的特点,明确该地区的出砂机理,为后续的防砂提供良好的条件;Shabdirova等[18]针对哈萨克斯坦弱固结储层容易出砂的问题,提出一个预测模型,该模型预测与当地油田的实测砂量也比较吻合,结果表明塑性区的渗透性是预测结果中最显著的控制因素;Li等[19]提出了一种基于有限元的模拟出砂过程的方法,通过对裸眼和射孔套管完井出砂过程的模拟表明,井筒的出砂主要受塑性应变和流动速度的影响,同时压降、地应力和射孔方向,都对出砂速率有影响;Ghassemi等[20]采用一种晶格波兹曼法和离散元耦合的方法进行二维模拟,对弱胶结砂岩油藏的油井出砂现象进行模拟,结果表明,出砂量的大小很大程度上取决于流量和围压,在特定流量下累积出砂量随围压的增大而减小,对所有围压下,超过临界流速会导致出砂速率显著增加。

目前出砂的研究工作主要集中在中浅地层,对深层、超深层气井出砂的研究较少,与中浅部油气藏模型不同,深层、超深层气藏的开采模型需要考虑储层高温、高压和高应力特征。分析深层气井开采过程需要基于热-流-固耦合理论。因此,现结合中国超深层气藏的环境条件和地质特征,以克深地区致密砂岩储层为研究对象,针对深层气井开发过程中的出砂问题,结合热-流-固耦合模型,建立考虑高温、高压、高应力状态下的出砂模型,探究深层气井出砂影响因素,揭示出砂规律,为中国深部气藏开发提供开采依据。

1 力学实验

实验所用岩心取自克深区块致密砂岩储层,实验开始前,将砂岩岩心制备成直径25 mm,长50 mm的标准圆柱体试样。实验过程模拟深部储层的温度和压力,并由实验获取数值模拟所需的力学参数。

为测得不同条件下岩石破坏时的岩石力学参数,构建高温高压条件下砂岩破裂准则,揭示高温、高压下岩石的破坏机制,分别进行了不同温度和围压下的三轴力学实验,力学实验共进行12组,实验条件为:围压30 MPa和60 MPa,实验温度为80、100、120、140、160、180 ℃。

利用现场取回的岩样,进行不同温度和围压条件下的三轴实验。将制成的标准岩样用上、下施压块加紧并包裹热缩管,外面装好变形传感器,安装在高压实验筒内。给高压实验筒内充油,打开温度控制系统给实验筒内液压油加热升温,当液压油温度达到所需温度后,控制围压系统施加围压,通过轴向位移控制系统给岩心施加轴压,直至岩心破坏后停止加压,实验结束。实验所得应力-应变曲线如图1所示,其中,图1(a)～图1(f)分别表示岩心温度在80～180 ℃下,围压为30 MPa和60 MPa时的应力-应变曲线。

图1 应力-应变曲线Fig.1 Stress-strain curve

不同温度和压力条件下三轴实验得到的岩心的弹性模量和峰值强度如图2 (a)、图2(b)所示,当温度由80 ℃上升到180 ℃,围压为30 MPa时,岩石的弹性模量降低约10 GPa,峰值强度降低约 83 MPa;围压为60 MPa时,岩石的弹性模量降低约6 GPa,峰值强度降低约89 MPa。随着温度升高,弹性模量和峰值强度下降,岩石强度降低。

图2 三轴实验结果Fig.2 Triaxial test results

从实验结果看,不同温压条件下试样均发生了剪切破坏。不同温度下的摩尔圆如图3 (a)～图3(f)所示,可以看出高温下的摩尔库伦包络线呈非线性,回归得到该区块不同高温下岩石的破裂准则模型为

图3 摩尔圆Fig.3 Mohr’s circle

τ=498.55T0.54lnσ-3 873.8T0.835

(1)

式(1)中:σ为正应力,MPa;τ为剪应力,MPa;T为温度,℃。

基于摩尔-库仑破坏准则计算了不同温度下岩石的内聚力和内摩擦角,计算结果如图4所示。储层岩石的内聚力和内摩擦角都随着温度的升高而逐渐降低,当温度从80 ℃升高到180 ℃时,岩石的内聚力从43.40 MPa下降至35.11 MPa,岩石的内摩擦角从24.24°下降至18.02°。

图4 内摩擦角、内聚力Fig.4 Cohesion and internal friction angle

综合分析可知,温度从80 ℃升高到180 ℃,会导致岩石强度降低,岩石本身的微结构更易受到损伤。

2 开采出砂模型建立

2.1 热-流-固耦合基本模型

2.1.1 地层多孔介质热-流-固耦合下的温度场模型

地层骨架的热平衡方程为

(2)

式(2)中:Cs为地层骨架比热,J/(kg·K);λs为地层骨架导热系数,W/(m·K);Ts为骨架温度,℃;ρs为地层骨架密度,kg/m3;φ为孔隙度;Qs为地层骨架热产率。

基于能量守恒定律,得到温度场的控制方程[21]为

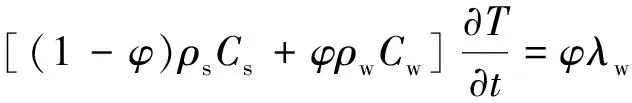
(1-φ)λs∇2T-ρwCw∇·(TwV)+Qs

(3)

式(3)中:Cw为孔隙流体比热,J/(kg·K);ρw为流体密度,kg/m3;λw为流体导热系数,W/(m·K);Tw为流体温度,℃;V为介质速度,m/s。

2.1.2 地层多孔介质热-流-固耦合下的渗流场模型

假设流体可以自由流动,骨架颗粒体积和孔隙流体体积组成的连续性方程为

(4)

式(4)中:

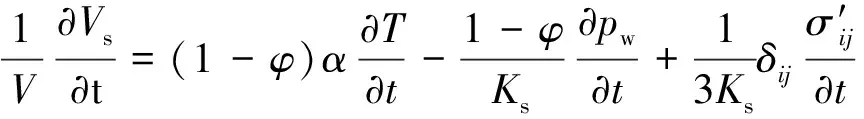
(5)

(6)

式中:Ks为地层骨架体积模量,MPa;Vs为骨架颗粒流速,m/s;Vw为流体流速,m/s;εv为体积应变;pw为流压,MPa;δij为应力张量分量;σ′ij为有效应力,MPa;qw为流体流速,m/s;αw为热膨胀系数,℃-1;Kw为流体体积模量,MPa。

将式(4)～式(6)联立得到连续方程,即

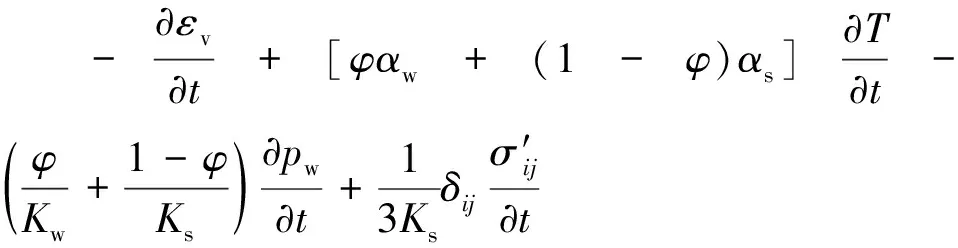
(7)

当忽略介质热渗透影响时,连续性方程表示为

qw=-k∇(pw+ρwgz)

(8)

式(8)中:k为渗透率张量。

联立式(7)和式(8),得到渗流方程表达式为

(9)

式(9)中:

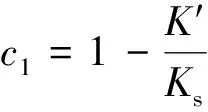
(10)

(11)

(12)

K′=[2G(1+v)/3(1-2v)]

(13)

2.1.3 多孔介质热流固耦合下的应力场模型

忽略惯性影响,动量平衡方程表达式为

σij,j+fi=0

(14)

式(14)中:σij,j为应力分量对坐标的偏导数;fi为多孔介质的体力分量。

fi=(0,0,ρmg)T

(15)

式(15)中:ρm为多孔介质的等效密度,kg/m3;g为重力加速度,9.8 m/s2。

ρm=φρw+(1-φ)ρs

(16)

式(16)中:ρw为水的密度,kg/m3;ρs为地层骨架密度,kg/m3;φ为孔隙度。

应力-应变本构关系表达式为

σij=2Gεij+λδijεv-βδij(Ts-Ts0)+

αδij(pw-pw0)

(17)

式(17)中:G、λ为弹性常数;δij为应力张量的分量;εv为体积应变;β为热应力系数;Ts为多孔介质的温度,℃;Ts0、pw0为初始参考值;α为比奥系数。

β=(2G+3λ)αs

(18)

式(18)中:αs为骨架各向同性线热膨胀系数,℃-1。

变形几何方程和体积应变的计算公式为

(19)

εv=εkk=ε11+ε22+ε33

(20)

将式(14)、式(17)、式(19)、式(20)联立,得到应力场控制方程为

G(μi,j+μj,i)j+λδijμk,kj-βδijTs,j+αδijpw,j+

ρfi=0

(21)

2.2 弹塑性本构关系

2.2.1 屈服面

剪切屈服面函数为

F=Rmcq-ptanφ-c=0

(22)

式(22)中:φ为摩擦角,(°);c为黏聚力,MPa。

Rmc的计算公式为

(23)

受拉破坏准则的表达式为

Ft=Rr(θ)q-p-σt=0

(24)

式(24)中:σt为抗拉强度。

2.2.2 塑性势面

塑性势面函数为

(25)

式(25)中:ψ为剪胀角,(°);

Rmc的计算公式为

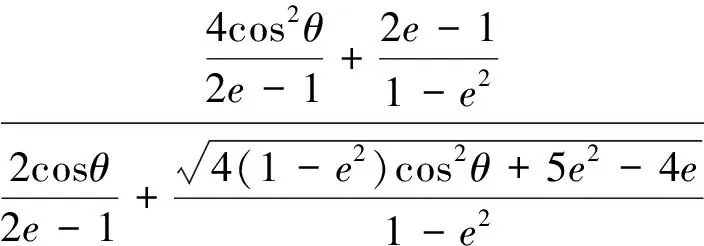
(26)

(27)

2.2.3 硬化规律

等效塑性应变为

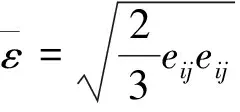
(28)

式(28)中:eij为偏应变张量。

2.3 出砂判别标准

由于在开采过程中,井眼周围的地层最容易受到破坏,从而在井眼附近出现一定范围的塑性应变。因此认为在进行数值模拟时,当井眼周围出现了塑性应变,则说明该区域有出砂的风险;反之,当井眼周围没有出现塑性应变,则说明地层不会出砂。在ABAQUS分析的过程中主要是根据塑性变形的数值大小和分布范围来确定出砂的风险大小的。主要通过等效塑性应变值(PEEQ)[22]的大小来判断出砂程度的大小。根据本构关系和三轴实验结果可得:如果等效塑性应变值PEEQ大于1%即认为地层出砂,危险性出砂的等效塑性应变临界值定为3%。当等效塑性应变值小于1%时认为地层不出砂,当等效塑性应变值在1%～3%时认为是可控出砂,即通过一定的防砂方式可以控制出砂量,当等效塑性应变值大于3%时认为地层出现危害性出砂[23]。

2.4 数值模拟模型

建立1/4的地层,设置井眼半径为0.108 m,边界尺寸为5 m × 5 m,其他边界条件和初始条件主要包括:地层初始温度,井筒温度,初始孔隙压力,井底压力,最大水平主应力,最小水平主应力,上覆岩层压力。基于建立的有限元数值模拟模型进行区块深部砂岩储层直井裸眼开采出砂模拟工作,储层基本参数如表1所示。

表1 克深区块典型砂岩储层基本参数

3 储层开采出砂影响因素分析

3.1 开采时间对深部储层开采出砂的影响

当生产压差为2 MPa,模拟开采180 d时,Mises应力最大值变化如图5所示。当生产时间为30～180 d 时,Mises应力最大值从88.56 MPa增加到97.96 MPa,可以看出井周Mises应力最大值出现在最小水平主应力方位,且随着生产时间的增大,井周最大Mises应力逐渐增加。

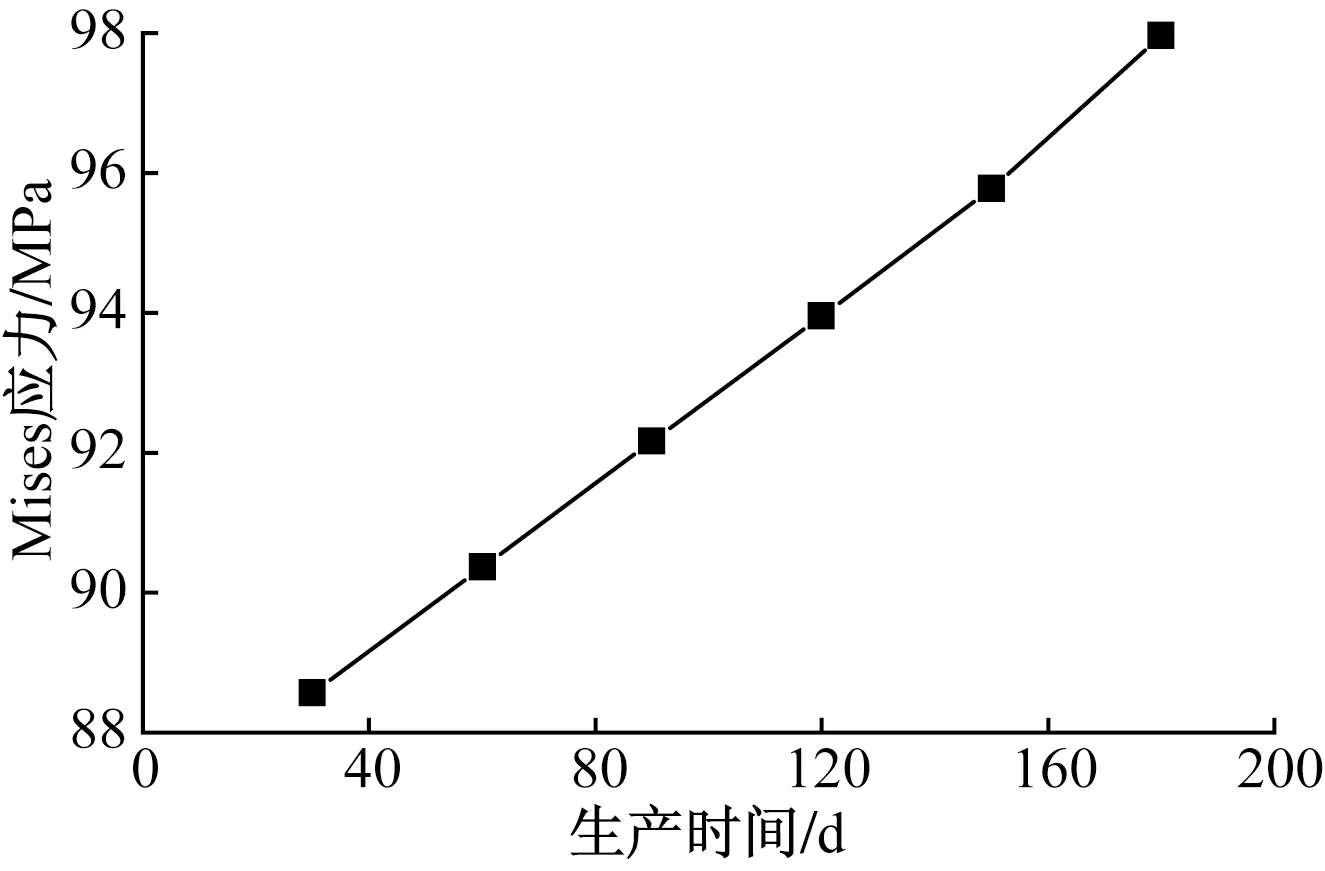
图5 Mises应力随时间变化Fig.5 Mises stress varies with time

等效塑性应变随时间的变化如图6所示,开采时间30～180 d时,等效塑性应变最大值从2.427%增加到2.939%。结果表明,开采时间越长,等效塑性应变越大,出砂风险越高。

图6 最大等效塑性应变随时间变化Fig.6 The maximum equivalent plastic strain varies with time

3.2 生产压差对深部储层开采出砂的影响

在保持其他参数一定的情况下,只改变生产压差大小,分析不同生产压差对深部砂岩储层出砂的影响。设置生产压差分别为1、1.5、2、2.5、3和 3.5 MPa,以开采时间180 d为例。井眼周围应力分布规律如图7所示。不同生产压差下的井周等效塑性应变如图8所示。模拟结果显示,生产压差越大,井眼周围最大Mises应力越大,等效塑性应变也越大,储层开采出砂风险也越大。

图7 Mises应力随生产压差变化Fig.7 Mises stress varies with different pressure

图8 不同生产压差下最大等效塑性应变Fig.8 Maximum equivalent plastic strain under different production pressure difference

根据不同生产压差下的最大等效塑性应变结果,通过回归可以得到最大等效塑性应变与生产压差之间的关系方程为

Y=0.003 2x2+0.012 3x+2.900 7

(29)

式(29)中:Y为最大等效塑性应变,%;x为生产压差,MPa。

根据等效塑性应变出砂判别标准,通过式(29)可以计算出目标区块气井裸眼开采严重出砂的临界生产压差为3.97 MPa。

3.3 地层温度对深部储层开采出砂的影响

温度是深部储层开采不可避免的影响因素之

一。高温环境会导致岩石力学性质劣化,进而影响深部储层开采出砂。利用控制变量法,在保持其他参数一定的情况下,只改变地层温度大小,分析不同地层温度下储层出砂规律。设置地层温度分别为80、100、120、140、160和180 ℃,开采时间为 180 d。井周应力分布规律如图9所示。

图9 Mises应力随温度变化Fig.9 Mises stress varies with temperature

不同地层温度下的井周等效塑性应变如图10所示。模拟结果表明,地层温度越高,井眼周围等效塑性应变越大。其结果说明地层温度越高,储层岩石强度越低,开采过程中容易发生剪切破坏,加剧出砂的风险程度。

图10 不同地层温度下最大等效塑性应变Fig.10 Maximum equivalent plastic strain at different formation temperatures

3.4 地应力对深部储层开采出砂的影响

由于深层气井可能会钻遇断层,地层构造应力的变化,以及生产动态的影响会导致水平地应力状态发生改变,从而影响储层开采出砂的风险程度,因此需要研究地应力对克深区块深部砂岩储层开采出砂的影响规律。通过改变最大、最小水平地应力来改变水平地应力非均匀程度,进而表征地应力的状态。

在保持其他参数一定的情况下,只改变水平地应力非均匀程度大小,分析不同水平地应力状态下克深区块深部砂岩储层开采出砂的规律。设置水平地应力非均匀程度大小如表2所示,开采时间为180 d。井眼周围应力分布规律如图11所示。

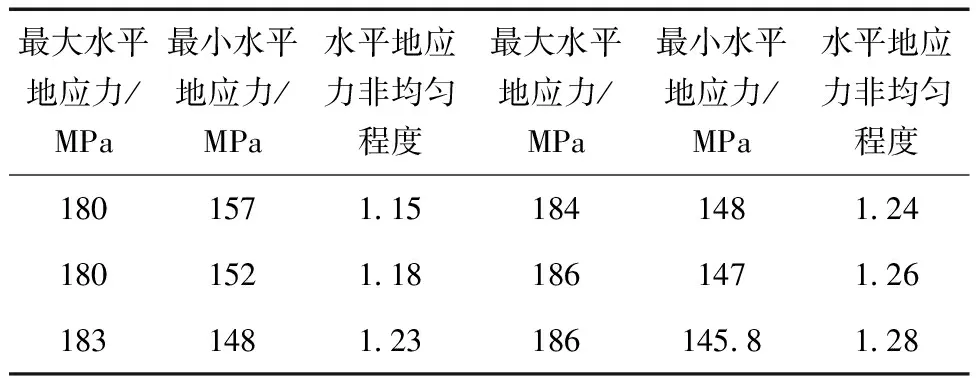
表2 水平地应力非均匀程度

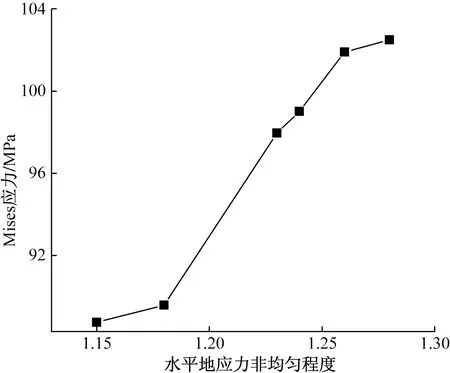
图11 Mises应力随水平地应力非均匀程度变化Fig.11 Mises stress varies with levels of ground stress heterogeneity

不同水平地应力状态下的井周等效塑性应变如图12所示。模拟结果表明,水平地应力非均匀程度越大,井眼周围的Mises应力最大值越大,等效塑性应变最大值也越大,储层开采出砂风险程度也越大。因此,需要在开发前进行地应力精确预测,了解地层地应力非均匀程度,对于该地区考虑地下生产动态等因素的影响,当水平地应力非均匀程度超过1.24时,需要提前实施防砂措施。

图12 不同水平地应力非均匀程度等效塑性应变Fig.12 Maximum equivalent plastic strain at different levels of ground stress heterogeneity

3.5 岩石胶结强度对深部储层开采出砂的影响

深层致密砂岩储层开采过程中,容易造成地层岩石胶结强度在一定程度上的降低,影响储层开采出砂的风险程度。通过内聚力表征岩石胶结强度,分析岩石胶结强度对储层开采出砂的影响规律。

在保持其他参数一定的情况下,只改变内聚力大小,分析不同岩石胶结强度对克深区块深部砂岩储层出砂的影响。根据室内实验结果,设置内聚力分别为35.11、37.25、38.11、41.04、42.61、43.40 MPa,开采时间为180 d。井眼周围应力分布如图13所示。

图13 Mises应力随岩石胶结强度变化Fig.13 Mises stress varies with cementation strength

不同内聚力下的井周等效塑性应变如图14所示。模拟结果表明,岩石胶结强度越大,等效塑性应变越小。说明岩石胶结强度越强,储层岩石破坏强度越高,开采时不容易发生剪切破坏,出砂风险程度低。随着开采过程中储层胶结强度不断下降,出砂的风险逐渐增加。

图14 不同岩石胶结强度下最大等效塑性应变Fig.14 Maximum equivalent plastic strain under different rock cementation strength

4 出砂影响因素敏感性分析

深层气井出砂的影响因素和各因素的水平数都比较多。为了判断上述影响因素对储层开采出砂的影响程度,寻找影响地层出砂的主控因素,采用正交试验设计方法进行计算。这里采用4因素3水平的正交表L9(34)进行方案设计。影响因素和水平值如表3所示,数值模拟结果如表4所示。

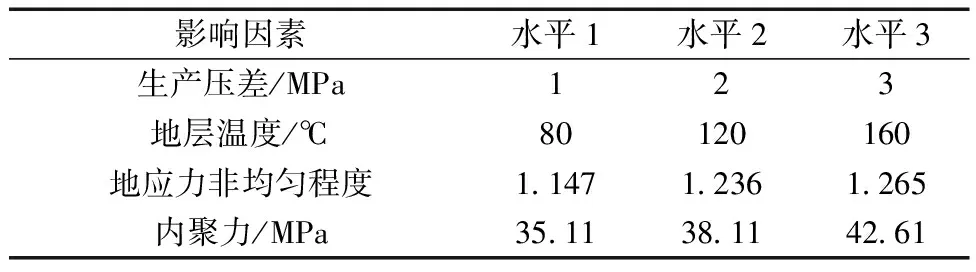
表3 影响因素和水平值

表4 正交试验结果L9(34)

用极差分析法进行出砂敏感性大小分析。其中所需的计算统计参数为

(30)

式(30)中:Kij为因素j在i水平下各次试验结果平均值;n为因素j在i水平下的试验次数;Yk为第k

个试验指标值。

各因素的极差值Rj是敏感性的评价标准,其计算公式为

Rj=max(Kij)-min(Kij)

(31)

对储层开采的出砂影响因素进行极差分析,计算各因素试验结果的平均值和极差值,得到敏感性分析的结果如表5所示。

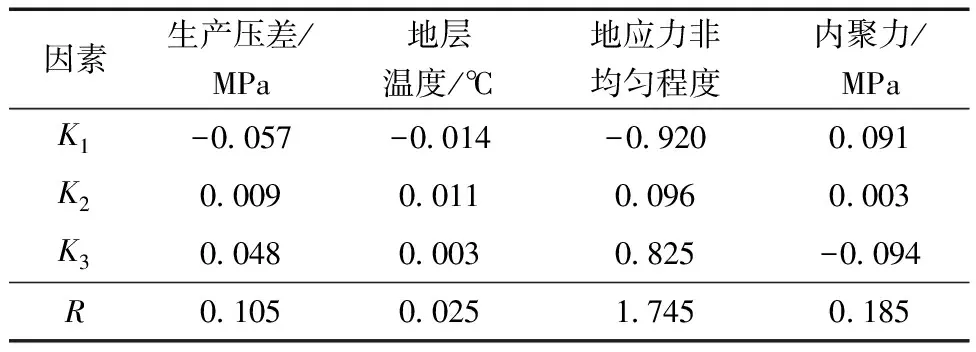
表5 影响因素极差分析结果

根据正交试验设计法,极差值越大,说明该因素的影响程度越大。由表5可知,极差值最大的影响因素是地应力非均匀程度,其次为岩石胶结强度和生产压差,极差值最小的影响因素是地层温度。因此,对于考虑的出砂影响因素中,地应力非均匀程度对克深区块深部储层开采出砂的影响最大,其次是岩石胶结强度和生产压差,地层温度对于开采出砂的影响较低。

5 结论

根据岩石力学实验得到了深部砂岩的力学参数,并依据此参数进行了数值模拟研究,得到以下结论。

(1)实验获得了深部砂岩储层的力学参数,实验结果表明:温度升高,岩石强度降低,岩石本身的微结构更易受到损伤。

(2)深层气井裸眼开采时,随生产时间增加,储层出砂风险增加;随着生产压差的增加,井眼周围Mises应力逐渐增大,应力集中现象在井眼周围明显,等效塑性应变逐渐增大,储层开采出砂的风险和严重程度增大。深层气井开采时,开采时间越长,出砂风险越大。地层温度越高,开采出砂风险和严重程度越大。水平地应力越不均匀,储层开采出砂风险和严重程度越大。岩石胶结强度越低,储层开采出砂风险和严重程度越高。

(3)通过正交试验法分析影响储层出砂的敏感性因素,表明:水平地应力的非均匀程度对储层开采出砂的影响最大,其次为岩石的胶结强度和生产压差,地层温度对储层开采出砂的影响最小。