矮塔斜拉桥分丝管索塔锚固强弱分区模型及试验研究
杜泽宇, 何磊, 王海鹏, 李佳文, 翟晓亮, 熊治华*
(1.中国铁建投资集团有限公司陕西公司, 西安 710000; 2.中交第一公路勘察设计研究院有限公司, 西安 710000;3.西北农林科技大学水利与建筑工程学院, 杨凌 712100)
斜拉桥的拉索与索塔之间的锚固区局部应力大、传力复杂,存在应力集中等现象,故锚固区设计极为重要。矮塔斜拉桥的索塔锚固区主要采用分层式索鞍,包括双套管和分丝管两种。对于分层式索鞍锚固区:刘钊等[1]研究了矮塔斜拉桥的双套管索鞍对连续通过拉索的黏结锚固性能,探讨了索鞍区的合理构造设计方法。刘尊稳等[2]研究了分丝管索鞍区混凝土应力的分布规律及其极限荷载。宋军等[3]探讨了矮塔斜拉桥分丝管索塔锚固区鞍座处混凝土的应力分布情况和索力传递分配情况。莫利君等[4]采用有限元软件,用实体单元模拟塔柱锚固区的钢索鞍分丝管,分析了塔柱索鞍区及塔柱分叉区的混凝土应力,并根据研究结果,建议在索塔分叉处的局部范围采用加强配筋等措施来改善塔柱分叉区受力。Tang等[5]分别采用有限差分法(finite difference method,FDM)和有限元法对分丝管锚固区进行了对比计算,结果表明与有限元解相比,除加载区域外,FDM的近似解可提高计算效率。但已有研究目前尚未讨论分丝管本身构造参数对结构受力性能的影响。此外,狄谨等[6]以某矮塔斜拉桥为工程背景,对耳板式索塔锚固区销铰的接触应力进行了求解,建议耳板材料用强度较高的钢材,且在销孔周围进行局部加强。李博[7]通过建立矮塔钢桁梁斜拉桥的索塔锚固区有限元模型,探究了承压板和锚垫板板厚等参数对矮塔斜拉桥锚固区力学性能的影响。另外,还有一些关于矮塔斜拉桥车-桥耦合效应等研究进展[8]。
对于常规斜拉桥,目前常用的锚固方式有钢锚箱、钢锚梁、预应力锚固等。针对这些锚固结构,开展了试验研究[9-12],分析了锚固区的应力分布与承载能力;在理论研究方面[13-16],探究了锚固区的受力特性与传力机理等力学性能;还有一些研究[17-20]为改善现有的索塔锚固结构的局限性,如施工不便、结构构造复杂等,提出了新型的锚固结构。
在工程设计中常需要对桥梁结构进行优化,以达到节省材料、造价经济的目的。拓扑优化作为结构优化方法中较常见的一种,可以根据给定的负载情况、约束条件和性能指标,在给定的区域内对材料分布进行优化。熊治华等[21]利用拓扑优化拉-压杆模型得到了斜拉桥索塔锚固区的有效传力区域退化模型;Guan等[22]对拱桥、系拱桥、斜拉桥和悬索桥的整体设计进行了拓扑优化;Li等[23]基于单一材料的双向演化结构优化(bidirectional evolutionary structural optimization,BESO)技术,提出了一种对多材料结构进行拓扑优化的方法。综上,鉴于拓扑优化方法的成熟和可靠性,将其应用于锚固区的研究中。
现以王家河特大桥为工程背景,结合现场原位试验,建立其索塔锚固区有限元模型,分析分丝管管径对索塔锚固区各构件应力情况的影响;通过建立分丝管锚固和交叉锚固有限元模型,对比两种锚固方式下构件的应力情况;采用拓扑优化得到分丝管锚固区的传力路径和优化构型。
1 工程概况及现场试验
1.1 工程概况
王家河特大桥位于陕西省铜川市,结构形式为矮塔斜拉桥,跨径组成为(125+4×230+125) m,墩和塔最高高度约为188.5 m,采用塔墩梁固结体系。其立面布置图如图1所示。

图1 王家河特大桥立面布置图Fig.1 The elevation view of Wangjia River Bridge
主塔与主梁为固结,桥面以上塔高36 m。塔柱采用实体截面,纵桥向塔柱桥面以上12 m范围内为渐变段,宽度由6 m直线变化至9 m,斜率为1∶8,上塔柱为等截面,宽度为6 m。横桥向尺寸为3.5 m。从美观上考虑,主塔4个角设(120×40) cm倒角,横桥向设20 cm深凹槽。
斜拉索为中央双索面,双排布置在主梁的中央分隔带处。塔上采用分丝管式索鞍结构,斜拉索在塔上连续通过,在索鞍一侧设置单根可换式单侧双向抗滑装置,实现拉索在索塔装置处的锚固,为与斜拉索通过鞍座相适应,分丝管中段采用圆弧形。斜拉索两侧对称锚于主梁,采用主梁侧单端张拉。每个索塔设有2×15对30 根斜拉索,全桥共150 根斜拉索,预张拉索力4 700 kN。
斜拉索采用单丝涂覆环氧涂层预应力钢绞线,单股钢绞线直径15.2 mm,标准强度fpk=1 860 MPa,每根斜拉索规格为:43股,直径15.2 mm,采用拉索群锚锚固体系。索塔结构示意及拉索布置如图2所示。索塔锚固示意图如图3所示。

图2 索塔结构示意及拉索布置图Fig.2 Structures of pylon and cables

图3 索塔锚固示意图Fig.3 Pylon anchorage zone
1.2 现场原位试验
对13号主墩索塔C4分丝管进行现场原位试验,选取C4分丝管下20 cm平面内的5个测点,利用JMZX-416AT型钢筋应力计测量钢筋应力,待中跨合龙2 d后读取测试数据。现场原位试验过程如图4所示,应力测点布置图如图5所示。4个测点位于分丝管中心线下方,1个测点位于索塔截面边缘。测点编号中的“V”表示测试钢筋为竖向钢筋,“H”表示测试钢筋为水平钢筋。

图4 现场原位试验Fig.4 In situ testing
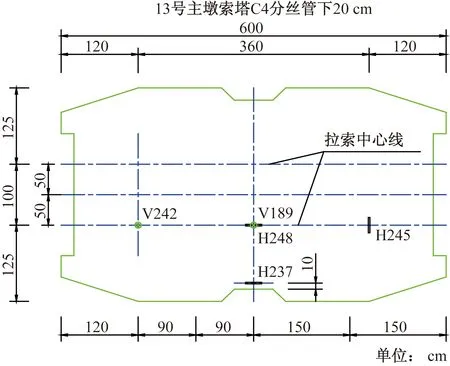
图5 应力测点布置图Fig.5 Layout of reinforcement stress measuring points
1.3 数值模拟与试验结果
通过有限元软件ABAQUS对王家河特大桥索塔锚固区试验进行数值模拟。将分丝管等效为环形曲线孔道,拉索等效为曲线圆柱体,考虑到拉索进出口抗滑装置的作用,将分丝管与拉索、分丝管与混凝土塔段接触设为绑定接触。模型边界条件为底面约束全部线位移,两个侧面只约束顺桥向位移。在塔段上下表面施加轴力及弯矩差值,索力以降温法施加在拉索等效圆柱体上。分丝管和拉索采用C3D8R实体单元和C3D10实体单元模拟,共3 990个,节点数共7 638个;索塔节段在分丝管附近区域采用C3D10实体单元,共68 687个,其余区域采用C3D8R实体单元,共22 232个,节点数共132 044个;普通钢筋采用truss单元模拟,共4 290个,节点数4 743个。构件网格划分如图6所示。

图6 网格划分Fig.6 Finite element meshing model
现场原位试验测点V242钢筋应力值为-12.15 MPa,有限元模拟结果为-12.05 MPa,误差为0.83%,校核结果较好。其余测点周围钢筋较多,由于钢筋导热特性,受测试过程中的混凝土水化热及温度梯度等影响,可能导致其他测点误差偏大。
2 分丝管索塔锚固区受力研究
2.1 分丝管管径对索塔锚固区应力的影响
以降温法施加预应力,计算公式为

(1)
式(1)中:F为预应力的幅值;αt为材料的热膨胀系数;E为材料的弹性模量;A为钢束的横截面积;T为数值计算输入的预应力等效温度。
根据实际结构,分丝管壁厚20 mm,将分丝管管径等效为360 mm,在相同的张拉索力下,对应的不同锚固区内力情况有所差异。为确保上述锚固区应力分布规律的准确性与适用性,分别取内索、中索、外索对应的锚固区塔段进行分析,其构件应力云图如图7和图8所示。

图8 分丝管主拉应力云图Fig.8 Contour plot of the strand deviating
从图7、图8可以看出,从内索区到外索区的不同索塔区段的拉索最大拉压应力无明显变化,分丝管最小压应力、最大压应力均在缓慢减小;拉索整体呈现出弧顶处受拉,然后向两端过渡到受压状态;分丝管整体受压,弧顶处压应力较小,向两端过渡时压应力逐渐增大。
由于分丝管管径的大小对拉索索力的传递、索体及索鞍周围混凝土的应力扩散均有一定的影响,故拟设计不同管径的分丝管进行分析,分丝管管径分别为280、300、320、340、360 mm,以探究分丝管管径对索塔节段各构件受力情况的影响。分别选取内索区、中索区、外索区的索塔节段进行计算,计算结果如表1~表3所示。

表1 内索区各构件应力情况

表2 中索区各构件应力情况

表3 外索区各构件应力情况
由表1~表3可知,随着分丝管外径的增大,分丝管的压应力逐渐减小;拉索的最大拉压应力先减小后增大,在分丝管外径为340 mm时,拉索最大拉压应力达到最小值;普通钢筋的最大拉应力无明显变化,普通钢筋的最大压应力在内索区时逐渐减小,中外索区时先减小后增大,在分丝管外径为340 mm时,钢筋压应力达到最小值。随着索塔节段向外推进,分丝管压应力缓慢减小,拉索拉压应力、普通钢筋拉应力无明显变化,普通钢筋压应力整体呈现减小趋势。
2.2 分丝管锚固与交叉锚固构件应力对比
交叉锚固与分丝管锚固是斜拉桥索塔锚固区常用的两种锚固方式,为探究两种锚固方式对于锚固区的受力影响,对两种锚固方式进行对比。在两种锚固方式下,保持拉索直径一致,斜拉索出入口的角度一致,边界及荷载条件一致,每层的普通钢筋等效面积一致,在此基础上探究两种锚固方式的受力特点。有限元整体模型如图9所示。两种锚固方式的构件应力对比如表4所示。

表4 两种锚固方式构件应力对比

图9 两种锚固方式有限元整体模型Fig.9 Finite element models of two anchorage zones
从表4可以看出,在不同索塔区段,分丝管锚固区的拉索应力均小于交叉锚固的拉索应力;分丝管锚固在内索区和中索区的普通钢筋应力均小于交叉锚固的钢筋应力,外索区分丝管锚固的普通钢筋应力大于交叉锚固的钢筋应力,两者数值均较小。整体来看分丝管锚固的应力情况要优于同条件下的交叉锚固。
3 分丝管索鞍强弱锚固分区构型
3.1 拓扑优化
拓扑优化的目的为寻找荷载的最有效传力路径。目前常用的拓扑优化方法有均匀化方法、变密度法、渐进结构优化法(evolutionary structural optimization,ESO法)、水平集法[24-27],采用变密度法对分丝管索塔锚固区进行优化。变密度拓扑优化法的基本原理是假设构成结构的材料密度与材料的某一个或几个物理参数存在函数关系,材料的密度在区间[0,1]取值。根据给定的优化方向(约束条件)对中间密度材料进行惩罚,使其迭代收敛于0/1材料分布。迭代后密度值为0的单元,其退化为孔洞;密度值为1的单元,即为找到的最为有效的传递荷载的单元和路径。
拓扑优化具体实施步骤为:①建立索塔锚固区的三维有限元模型,材料本构关系取为弹性材料;②对模型进行加载,将加载结果作为拓扑优化分析的初始步;③设定优化方向即约束条件(体积减小率),开始优化迭代;④利用迭代结果得出优化几何构型。
实施以上步骤,得到拓扑优化后的锚固区优化几何构型。索塔锚固区有效传力区域典型退化过程如图10所示,由此可知锚固区优化后的几何构型为分丝管附近混凝土成一度角度发散到索塔节段上下表面。由此可得出,分丝管索塔锚固区的空间传力机理为索力通过锚块传递至索塔壁,同时通过分丝管传递给周围混凝土,再传至索塔节段上下表面。
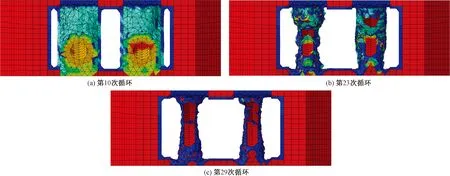
图10 索塔锚固区有效传力区域典型退化过程Fig.10 Typical degradation process of effective load transferring areas in pylon anchorage zone
根据图10绘制分丝管锚固拉索出入口周围混凝土的强弱锚固分区通用优化构型,如图11所示,优化构型被锚垫板分割为强锚压区与弱锚压区两部分,如图11(b)所示。设分丝管外径为d,通用优化区上边长s≈0.55 d,混凝土破坏角α≈56°。

图11 通用优化构型Fig.11 General optimized configuration
3.2 优化模型强度校核
得到锚固区优化构型后,对其进行强度校核,由于拉索出口处容易产生应力集中等不利现象,故对出入口处的强弱锚固分区通用优化构型混凝土进行强度校核。由于分丝管直径为280 mm时,拉索的拉应力最大,故采用该直径的索塔锚固区模型进行强度校核。分别对强锚压区与弱锚压区的应力状态进行强度校核,校核结果如表5所示。

表5 优化构型强度校核
桥塔采用C55混凝土,其圆柱体抗压强度标准值f′c= 0.79f′ck= 28.05 MPa。其抗拉强度标准值为ftk=2.74 MPa。根据表5结果可知,混凝土拉压应力均满足要求。
4 结论
以王家河特大桥为工程背景,结合现场原位试验,研究了矮塔斜拉桥分丝管索塔锚固区的应力情况,并与同等条件下的交叉锚固区进行了构件应力情况对比;对分丝管锚固区进行了拓扑优化,提出了分丝管索塔锚固强弱分区模型,得到以下结论。
(1)探究了分丝管管径对内、中、外索塔锚固区各构件的应力情况的影响。随着分丝管外径的增大,分丝管的压应力逐渐减小;拉索的最大拉压应力先减小后增大,在分丝管外径为340 mm时,拉索最大拉压应力达到最小值;普通钢筋的最大压应力在内索区时逐渐减小,中外索区时先减小后增大,同样在分丝管外径为340 mm时达到最小值。随着索塔节段向外推进,分丝管压应力缓慢减小,拉索拉压应力、普通钢筋拉应力无明显变化,普通钢筋压应力整体呈现减小趋势。
(2)将不同索塔区段下的分丝管锚固和交叉锚固受力情况进行对比,得到分丝管锚固区的拉索应力均小于交叉锚固的拉索应力;分丝管锚固在内索区和中索区的普通钢筋应力均小于交叉锚固的钢筋应力,外索区分丝管锚固的普通钢筋应力大于交叉锚固的钢筋应力,两者数值均较小。整体来看,分丝管锚固的应力情况要优于同条件下的交叉锚固。
(3)利用拓扑优化得到了分丝管锚固区的传力路径和优化几何构型,构建了拉索出入口周围混凝土的强弱锚固分区通用优化模型;并对该分区优化构型进行了强度校核,混凝土拉压应力满足要求。强弱锚固分区模型可为同类型的分丝管锚固结构提供设计理论依据。

