高速列车底部结构参数对气动噪声影响规律

陈 羽 ，柳壹明 ，毛 懋 ，李启良 ，王毅刚 ，杨志刚 ,3

（1.同济大学汽车学院，上海 201804；2.同济大学上海市地面交通工具空气动力学与热环境模拟重点试验室，上海 201804；3.北京民用飞机技术研究中心，北京 102211）

随着运行速度的提升，高速列车的噪声问题越来越显著，给环保和乘坐舒适性带来了更大挑战[1].当行驶车速大于300 km/h 时，气动噪声是列车噪声的最主要噪声源[2].传递路径分析技术发现[3]，转向架区域气动噪声的空气声传递为车内噪声最主要贡献源.

实车路试[4]、声学风洞实验[5]和数值计算[6]均表明高速列车转向架区域是列车主要的气动噪声源.Latorre 等[7]通过声学风洞试验研究了含有动力、拖车转向架以及纯空腔的转向架区域远场气动噪声，1/3 倍频程结果表明转向架本身产生的气动噪声水平很低，主要是腔体本身.

此前，高速列车气动噪声控制研究主要集中在头型的外形优化.Sun 等[8]用局部形函数法对某高速列车头型进行了参数化建模发现，影响远场噪声的关键变量在于流线型底部宽度以及车窗高度.张亮[9]基于多目标遗传算法（NSGA-Ⅱ）的优化设计和宽频带噪声计算模型指出，头车的排障器外形、头型水平最大外轮廓线与头车表面最大声功率的相关性较大.安翼等[10]采用非线性声学求解器和声学比拟法的混合算法，对不同头型长细比的高速列车远场噪声分析，发现增加长细比并不能明显提升气动噪声性能.目前高速列车转向架区域气动噪声控制主要考虑裙板控制[11]，对于转向架舱的系统参数化研究还很少，且文献主要关注远场噪声和车身表面湍流压力脉动，没有考虑降噪控制方法对近场噪声的影响[12].

从外形设计的角度，通过优化和控制列车底部的剪切层、旋涡脱落、再附着和流动反馈，能够降低气动噪声源的强度[13].本文以我国标准动车为对象，建立高速列车头车转向架区域的6 参数模型，通过计算气动声学和拉丁超立方实验设计的方法，研究底部结构参数对列车远场气动噪声、转向架舱内湍流脉动功率级和声功率级的影响规律，为高速列车的车内、外气动降噪设计提供帮助.

1 参数化模型

1.1 列车模型

研究对象为标准动车1∶8 缩比后的三车编组模型，其中头、尾车几何外形一致.模型几何尺寸L×W×H（长 × 宽 × 高）为10 200 mm × 420 mm × 506 mm，如图1（a）所示.列车模型由排障器、转向架舱、转向架、车辆连接处构成，并将模型表面部件进行了简化处理，其中拖车转向架设置在头、尾车，动力转向架设置在中间车.

图1 高速列车模型Fig.1 High-speed train model

1.2 头车底部结构参数化建模方法

高速列车头车第一组转向架区域是最主要的气动噪声源，头车底部结构由排障器、转向架舱和转向架（含轮对）构成，本文仅对底部结构参数对气动噪声影响规律开展研究.来流条件和舱几何结构是影响转向架区域气动噪声水平的主要因素[7].因此，针对转向架舱和排障器设计了6 个参数变量（转向架舱长度l、舱前缘倒角半径Rf、舱后缘倒角半径Rr、裙板高度h1、排障器厚度h2、排障器前缘夹角θ，如图2 所示），并保证车体断面形状不变.底部结构参数变化范围以我国高速列车CRH、标准动车组为参考，具体变化范围如表1 所示.

表1 参数变化范围Tab.1 Ranges of parameters

图2 头车底部结构参数模型Fig.2 Parameterization of underbody structure

1.3 基于拉丁超立方的数值实验设计

拉丁超立方抽样是一种分层随机抽样技术，由McKay 等[14]提出，能够从变量的分布区间进行高效采样.Iman 等[15]进一步发展了该方法，依照取样次数，把每个变量的取值区间均匀切割，在每个切割区间随机选取好点后再将各变量随机组合，以此来设计样本矩阵的参数，改进后只要取样次数大于变量数即可.

底部结构包含6 个控制参数，本文共设计12 次模拟，加上列车原型，共有13 个样本点.使用Isight软件的DOE (design of experiment)实验设计模块，在表1 所设计的列车底部结构参数样本空间抽选了12 个样本，如表2.

表2 高速列车底部结构参数化实验设计Tab.2 Design of experiment table of high-speed train under body parameters

2 数值仿真方法

2.1 计算模型

计算域如图3（a）所示，入口设计为距头车鼻锥1/4L，出口设计为距尾车鼻锥1/2L，车体中心线到计算域两侧的距离为1/4L，高度选择为10H.采用速度入口，来流速度250 km/h，入口湍流度为1%，湍流黏性比为10，出口为压力出口，计算域两侧和顶部为对称边界条件，其他为无滑移边界条件.

图3 计算域及网格Fig.3 Computational domian and grid

采用STARCCM + 的切割体和边界层组合方法生成空间体网格.边界层网格第一层厚度为0.02 mm，由此得到的近壁无量纲厚度y+≈1，满足数值方法的要求.一共生成12 层边界层网格，增长率为1.2.声扰动方程的求解域如图3（b）所示，体网格尺寸为3 mm，在声源和声传播过渡区采用汉宁窗处理以避免声波信号的阶跃.针对计算域设置了加密区，如图3（c）所示.可穿透声源面如图3（a）粉色区域所示，长12.64 m、宽0.84 m、高0.76 m，排障器和转向架舱内加密区体网格为3 mm，可穿透声源面上网格为12 mm，体网格总数约4 800 万.

2.2 计算方法

采用商业软件STARCCM + 进行求解.风速为250 km/h，马赫数小于0.3，非定常流场计算采用不可压大涡模拟并结合壁面适应局部涡粘模型（WALE），相比Smagorinsky 模型该模型不需要任何形式的近壁阻尼，能自动给出准确的壁面比例系数，是近年使用较广泛的湍流模型之一.使用SIMPLE 方法进行压力与速度场耦合.采用考虑声源运动和固壁效应的FW-H 方程计算远场噪声，通过求解APE 获得近场声压[16].初始化定常流动、非定常流动和气动噪声的计算方法与文献[12]相同，13 个样本点在168 核刀片服务器完成计算，总耗时78 d.

2.3 数值方法验证

在同济大学气动-声学整车风洞对1∶8 缩比三车编组的标准动车模型进行气动噪声试验，模型为可机加工树脂板材包裹钢骨架制成，车轮下部安装轨道，如图4（a）所示.设计了每个转向架舱后部薄翼型支撑，多点固定方式将模型安装在试验段地板上，以减小支撑干扰，试验风速250 km/h.选用3 个远场测点来收集试验模型远场噪声情况，测点布置在试验模型右侧.远场测点距试验模型中截面7.5 m，离地高度为0.8 m，各测点相距3.0 m，如图4（b）所示.

图4 风洞实验和远场测点Fig.4 Wind tunnel experiment and far-field measuring points

针对高速列车模型，以不同网格尺度划分了3 套不同数量的网格进行对比分析.时均气动阻力系数（Cd）作为参考，不同网格量的计算结果如表3.由表可知，当网格量大于4 900 万时，继续增大网格量对结果的影响较小，偏差在1%以内.风洞试验和数值计算得到的各测点总声压级结果如表4 所示，测点2 的总声压级量值仅相差0.3 dB(A)，靠近头车的测点1 和靠近尾车的测点3 总声压级分别与实验结果相差0.4 dB(A)和2.0 dB(A).

表3 网格敏感性验证Tab.3 Gird sensitivity verification

表4 测点总声压级Tab.4 OASPL of measureing points dB(A)

图5 给出了远场测点2 利用风洞试验和数值计算得到的声压级频谱，两者频谱变化趋势一致.2 kHz以上计算值低于试验值，是因为网格不够密导致高频能量耗散所致.结合表3 可见，远场噪声的数值仿真能获得与风洞试验相当的结果，表明远场噪声的预测合理.本文考虑列车噪声对外部环境中人[2]和车内乘客[3]的影响，因此，采用A 计权对噪声信号进行分析.

图5 测点2 的声压级频谱Fig.5 Noise spectrum of point 2

3 底部结构参数对气动噪声影响规律

3.1 底部结构参数对远场气动噪声的影响

底部结构参数会使得远场指向特性发生变化，单一测点无法客观反映参数对噪声水平的影响.高速列车气动噪声源可以认为是线声源，因此，将距离模型中心线7.5 m、高度为0.8 m 的5 个测点能量平均声压级作为降噪的评价指标，高度基准点为轨道下表面.其中，测点1 与头车鼻锥平齐，各测点相距0.564 m，如图6 所示.

图6 测点1～5 示意Fig.6 Schematic diagram of points 1-5

图7 为测点1～5 平均声压级，由图7 可知：样本点远场平均声压级的变化范围为75.4～78.9 dB(A)；相对于原型76.5 dB(A)，7 个样本点平均声压级增大，5 个样本点减小；其中，平均声压级最小的样本4较原型降低了1.1 dB(A)，平均声压级最大的样本11较原型增加了2.4 dB(A).

图7 测点1～5 平均声压级Fig.7 Mean sound pressure level of measureing points 1-5

为了分析底部结构参数对远场噪声的影响，给出各参数与远场噪声平均声压级的相关系数，如图8 所示.对于优化拉丁超立方样本点分布，其为非正态分布，采用Spearman 的秩相关系数来评估，该相关系数的大小代表了底部结构各个参数与远场噪声之间的单调关系.相关系数（式（1））取值范围为[-1,1]，相关系数为负即为负相关，表示随着参数数值增加平均声压级能量单调减小；相关系数为正与之相反.

图8 底部参数与远场噪声相关性系数Fig.8 Correlation between underbody parameters and noise in the far field

式中：x为样本点结构参数数值的等级参数；y为样本点平均声压级数值的等级参数；分别为样本点结构参数数值和平均声压级数值的等级参数的均值.

图8 为各参数的远场噪声相关性系数，由图8可知：对于远场测点平均声压级，l、h1、Rr和h2均为负相关，表明上述4 个参数取值增大，则远场噪声减小；Rf和θ均为正相关，表明其取值增大，远场噪声增大；Rf、θ、h1与远场噪声之间均具有较高程度的单调性关系；从头车转向架区域气动噪声控制的角度，减小θ、Rf或者增大h1、h2、Rr均可降低远场气动噪声水平；l的相关性系数为 -0.116，该参数为弱相关性.

图9 为远场噪声1/3 倍频程谱，由图9 可知：以原型为基准，中心频带1 250 Hz 以下时，底部结构参数可以使噪声能量减小；底部结构参数的改变主要使800～1 250 Hz 范围内的噪声能量增大，样本点11在该频带能量大幅增加，结合表2 可知增大裙板高度可以有效降低该频带的远场噪声水平；对于所有样本点，中心频带2 kHz 以上的极差值均在3 dB(A)以内.

图9 远场噪声1/3 倍频程谱Fig.9 1/3 octave band spectrum in the far field

3.2 底部结构参数对近场气动噪声的影响

3.2.1 对近场湍流脉动功率级的影响

湍流脉动压力以振动形式通过车身结构传入车内，以脉动力偶极子源形式向远场传播.通过大涡模拟计算得到大车体表面静压的时域信号，之后进行快速傅里叶变换（FFT）得到脉动压力级，参考压力为2 × 10-5Pa.

图10 给出了原型和各样本的底部湍流脉动压力级分布云图.结合表2 可知：排障器底部前缘低脉动压力级分布的样本点4、5、7、8、9、10、12 其θ均小于117°，表明排障器前缘外形为尖型时，排障器的湍流脉动压力级降低；转向架舱后缘低湍流脉动压力级分布的样本点2、4、5、7、8、9 其裙板高度均为79～98 mm，排障器厚度均为35～49 mm，增大裙板高度和排障器厚度可以明显降低头车转向架舱后缘的湍流脉动压力级水平；转向架轮对和构架下部低湍流脉动压力级分布的样本点2、4、7、8 其前缘倒角均小于6°，同时排障器厚度均为38～49 mm，转向架舱前缘无倒角和增大排障器厚度可以有效降低轮对和构架下部的湍流脉动压力级.

图10 头车底部表面湍流脉动压力级Fig.10 Surface turbulent fluctuating pressure levels at the bottom of the head car

对转向架舱前壁、顶部和后壁的湍流脉动压力级进行面积积分求和，得到转向架舱的湍流脉动总功率级，如图11 所示.由图11 可知：转向架舱内湍流脉动功率级的变化范围为121.3～124.7 dB(A)；相比原型工况122.9 dB(A)，4 个样本点增加0.5 dB(A)以上，2 个样本点减小0.5 dB(A)以上；最低湍流脉动总功率级降低了1.6 dB(A)，为样本点2，最高湍流脉动总功率级增加了1.8 dB(A)，为样本点12.

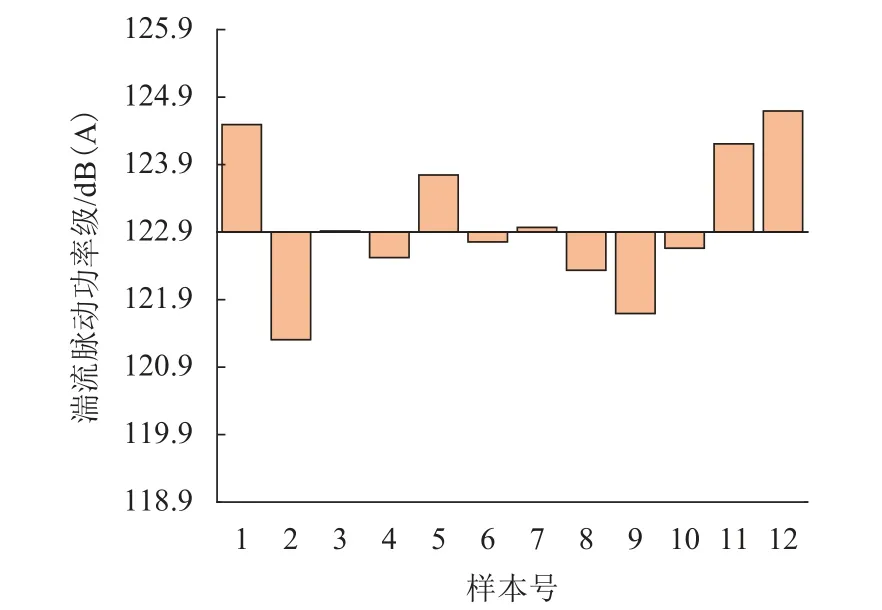
图11 舱内湍流脉动总功率级Fig.11 Total power level of turbulent fluctuation inside cavity

图12 为各参数与舱内湍流脉动总功率级的相关系数.

图12 各参数对舱内湍流脉动总功率级的相关系数Fig.12 Correlation between underbody parameters and total power level of turbulent fluctuation inside cavity

由图12 可知：h1、Rr和h2为负相关，随上述3 个参数取值增大，舱内湍流脉动功率级减小；l、Rf、和θ均为正相关，随上述3 个参数取值增大，近场湍流脉动功率级增大；随着舱长度增加，表面湍流脉动级有所减小，同时面积增大，导致转向架舱内脉动功率级与舱长度为正相关；结合3.1 节可知，h1、h2、Rf、Rr、θ的远场噪声和舱内湍流脉动功率级的相关性系数符号一致.

3.2.2 对近场湍流声功率级的影响

通过声扰动方程计算得到近场声波.声波在大部分频率范围与车体板件弯曲波的波数接近，而湍流压力的波数仅在低频区域和板件的弯曲波波数接近[17]，对于车内噪声，近场声波具有更高的传递效率.

图13 给出了原型和各样本的声压力级云图.结合表2 可知，排障器底部前缘低声压级分布的样本点2、4、5、7、8、9、10、12 其θ均小于117°，排障器前缘外形设计为尖型时，排障器上的声压级也会降低；转向架舱侧缘低声压级分布的样本点10、11、12 其裙板高度均在0～65 mm 内，减小裙板高度会降低头车转向架舱侧缘的声压级水平；转向架轮对和构架下部低声压级分布的样本点7、8、10、12 其排障器厚度均为35～49 mm，增大排障器厚度可以降低轮对和构架下部的声压级.

图13 头车底部声压级云图Fig.13 Sound pressure levels at the bottom of the head car

对转向架舱前、顶和后壁的声压级进行面积积分，得到转向架舱内总声功率级，如图14 所示.由图14 可知：转向架舱内声功率级的变化范围为111.7～116.8 dB(A)；相比原型的声功率级114.3 dB(A)，5 个样本点增加1 dB(A)以上，3 个样本点减小1 dB(A)以上；最低声功率级降低了2.6 dB(A)，为样本点12，声功率级最大的样本点增加了2.5 dB(A)，为样本点3.

图14 舱内总声功率级Fig.14 Total sound power level inside cavity

图15 为各参数与舱内总声功率级的相关系数.由图15 可知：l、Rf和h2为负相关，随上述3 个参数取值增大，近场声功率级减小；h1、θ均为正相关，随上述2 个参数取值增大，近场声功率级增大；h1的相关性系数为0.737，其与舱内气动噪声有较高程度的单调性关系；l、Rf、Rr相关系数分别为 -0.027、-0.198、0.033，这3 种参数与近场声功率为弱相关；结合3.1、3.2.1 节可知，h2、θ的远场噪声、舱内湍流脉动功率和声功率的相关性系数符号一致.

图15 各参数与舱内总声功率级的相关系数Fig.15 Correlation between underbody parameters and total sound power level inside cavity

4 结 论

1） 头车第1 组转向架区域底部结构参数对列车气动噪声水平有重要影响.对于1∶8 的缩比模型，远场噪声平均声压级变化范围为75.4～78.9 dB(A)，其舱内湍流脉动功率级变化范围为121.3～124.7 dB(A)，声功率级的变化范围为111.7～116.8 dB(A).

2） 对于远场噪声，转向架舱长度、裙板高度、转向架舱后缘倒角和排障器厚度与其为负相关，舱前缘倒角、和排障器前缘夹角与其为正相关，主要影响中心频带315～1 250 Hz 的噪声能量.

3） 对于头车转向架舱内湍流脉动功率级，裙板高度、转向架舱后缘倒角、排障器厚度与其为负相关，转向架舱长度、舱前缘倒角和排障器前缘夹角与其为正相关；对于舱内的声功率， 转向架舱长度、舱前缘倒角、排障器厚度与其为负相关，裙板高度和排障器前缘夹角与其为正相关.

4） 排障器厚度和前缘夹角与远场噪声、舱内湍流脉动功率、声功率均为负相关.裙板高度和远场噪声、舱内湍流脉动功率级为负相关，其与舱内声功率为正相关.