含双向变流装置的城轨牵引供电系统协同供电潮流计算

刘 炜 ，曾佳欣 ，马庆安 ，张 戬 ，熊 蓬 ，戚 贺

（西南交通大学电气工程学院，四川 成都 610031）

目前，国内多条地铁线路采用“整流机组 + 逆变回馈装置”供电方案，将大部分再生制动能量返回中压环网，使其得以有效利用[1].但由于整流机组的自然下垂特性，牵引变电所在整流时的直流输出电压随负荷波动较大，从而增大跨区间传输的电流，导致钢轨电位过高.双向变流装置（bidirectional converter device，BCD）具备四象限工作能力，从原理上能替代能量单向传递的二极管整流机组，提升正向牵引供电能力[2].但对城轨供电而言，要实现BCD 完全替代整流机组，需具备和原整流机组相同的容量，不仅增大投资成本，对装置效率、系统可靠性也有较高要求.故现阶段可考虑采用BCD 与整流机组协同供电的方案.

BCD 本质上为可逆变流器，在电力系统的应用已较为成熟，其控制技术、潮流计算模型可为牵引供电系统的相关研究提供参考依据[3-5].文献[6-7]均提出了一种由24 脉波整流机组（pulse rectifier unit，RU）和BCD 组成的混合型供电方案，并采用下垂控制策略，实测验证了该方案及策略的可行性、节能性及其对直流网压、越区供电等影响， 但未对该混合型供电方案在牵引供电系统中大规模应用后的潮流进行分析.

文献[8-9]建立了考虑下垂输出外特性的BCD计算模型，采用交直流一体迭代潮流算法，对含BCD 的城市轨道牵引供电系统进行潮流计算.文献[10]针对含可逆变流器的牵引供电系统，提出了一种考虑多个牵引变电所之间再生制动能量分配，具有最优潮流分层结构的直流电压下垂控制方案，并提出了基于牛-拉法的交直流顺序潮流算法， 为BCD 与整流机组协同供电时牵引供电系统的潮流计算提供了参考.

本文首先分析BCD 与24 脉冲整流机组协同供电时牵引变电所的综合输出外特性，建立其在不同运行状态下的直流等效电路模型；在此基础上，建立了计及换流装置精确有功损耗的牵引变电所供电计算模型，提出考虑滞环比较的多状态切换控制策略和交直流交替迭代算法；通过与Simulink 平台仿真结果对比，验证模型及算法的有效性及准确性；最后，结合地铁工程案例，研究协同供电方案对系统节能、钢轨电位及综合成本的影响.研究结果为BCD与RU 协同供电方案的大规模应用提供理论依据.

1 综合输出外特性分析

设RU 在协同供电时正常工作的下垂率恒为k1，空载电压为Udr；BCD 逆变、整流时的启动电压分别为Udi、Ud0，下垂率为k2，两者外特性见图1.图中：红、蓝色曲线分别表示BCD、RU 的外特性；Ud、Id分别为直流侧牵引网网压、输出电流；Ilimr（Ilimi）、Ulimr（Ulimi）分别为BCD 整流（逆变）工况下保持线性下垂特性时的最大输出电流、直流网压；I1为协同供电时牵引变电所的起始电流；I2为直流网压为Ulimr时RU 的输出电流.

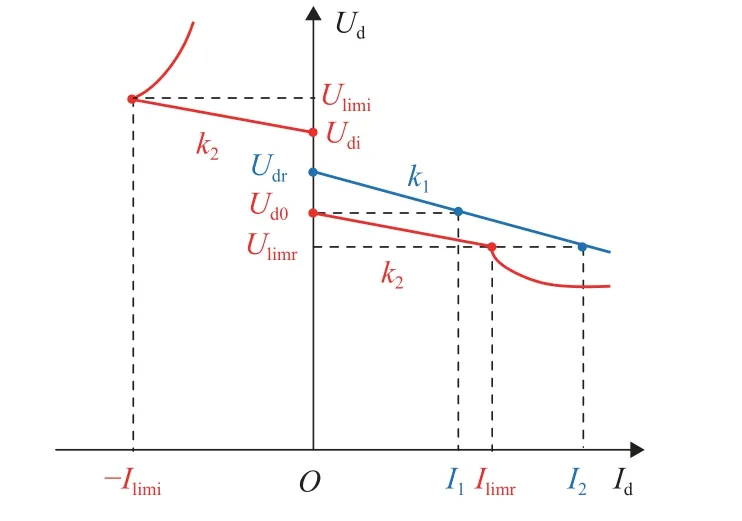
图1 BCD 与整流机组下垂特性Fig.1 Droop characteristics of bidirectional converter and rectifier unit

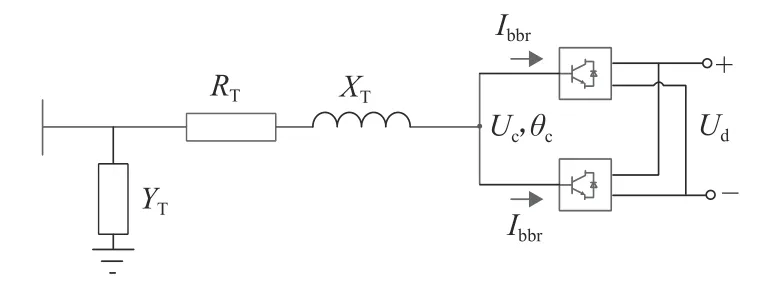
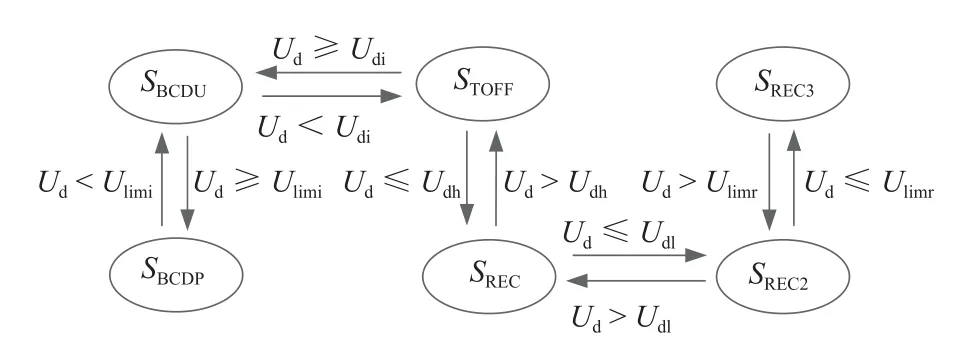
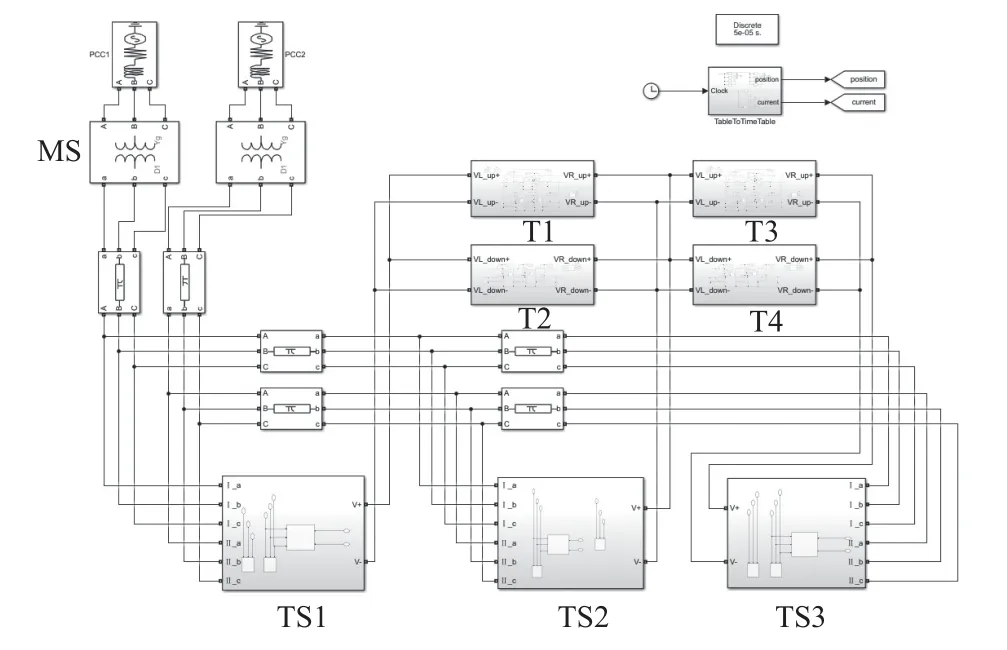
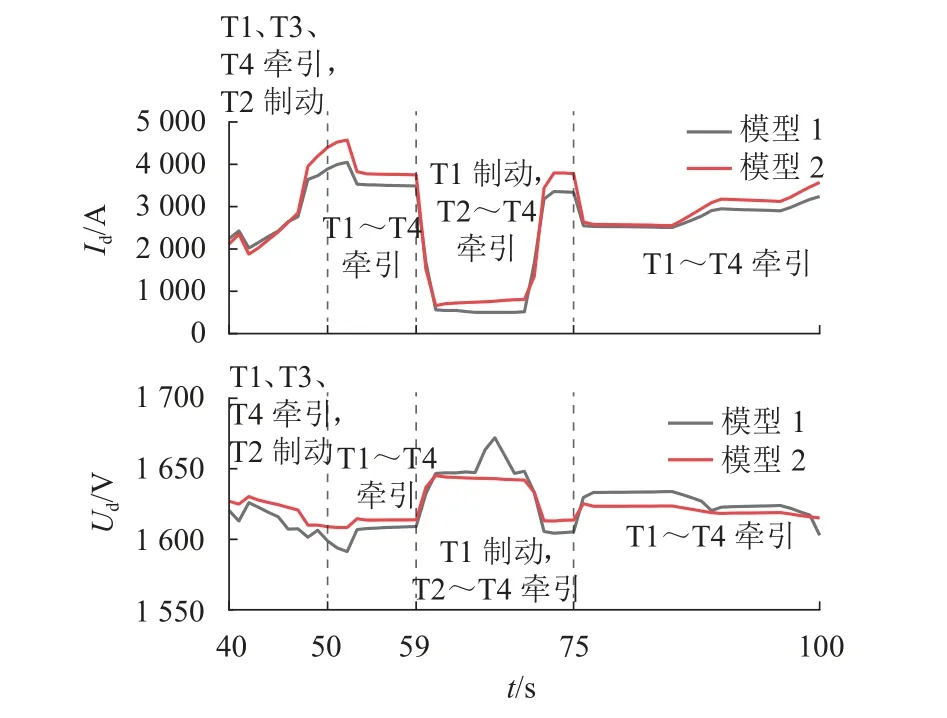
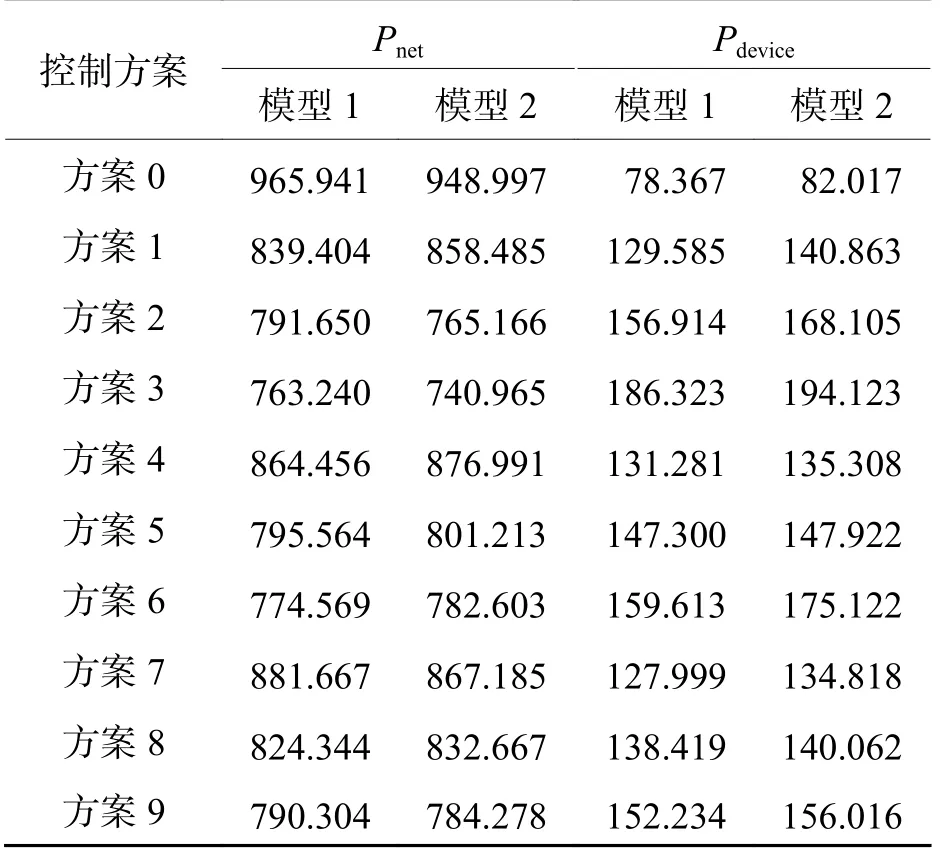
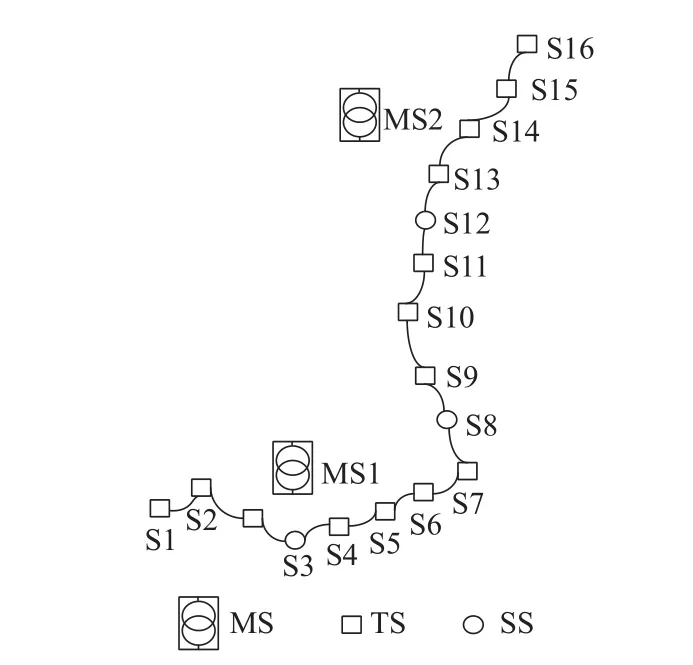
将协同控制策略分为Udr>Ud0、Udr=Ud0、Udr

图2 牵引变电所综合输出外特性Fig.2 Integrated output characteristics of traction substations

按Ud划分，牵引变电所共包含以下6 种运行状态.1）SREC：RU/BCD 单独整流，下垂率为kd0.2）SREC2：二者协同整流，下垂率恒为k.3）SREC3：二者协同整流，且BCD 保持最大功率运行.4）STOFF：关断.5）SBCDU：BCD 逆变下垂.6）SBCDP：BCD 保持最大功率逆变.特殊地，对于Udr=Ud0策略，由于BCD 始终与RU 协同供电，故无SREC.

输出外特性可用式（1）统一表示，Udr>Ud0时，kd0=k1；Udr

根据式（1）可建立牵引变电所在SREC、SREC2、SBCDU下的直流侧戴维南等效模型，等效电压源、电阻分别为Eeq、Req；经计算，牵引变电所工作在SREC3时，实际外特性近似线性，考虑到直流牵引网运行时允许的最低网压Udmin限制，可取Ud为Ulimr、Udmin对应的点计算出Eeq、Req；对于SBCDP，按SB等效为功率源模型.

2 牵引供电系统协同供电计算

2.1 计及换流装置精确有功损耗的牵引变电所协同供电计算模型

协同供电方案下，牵引变电所的交直流接口模型如图3 所示.图中：Us、θs、Is、 φs分别为系统交流侧节点电压、相角、电流、功率因数角；Ps、Qs分别为系统交流侧节点有功、无功功率；Edpos、Edneg分别为牵引变电所直流侧正、负节点电压；Idr、Idb分别为RU、BCD 直流侧注入电流.

图3 牵引变电所交直流接口模型Fig.3 AC-DC interface model of traction substations

牵引变电所整流时的供电计算模型如式（2）所示.

式中：Idpos、Idneg分别为直流侧正、负节点注入电流；Pdevice为协同供电方案下RU 与BCD 的运行损耗之和；PRT、PRb分别为RU 中变压器、三相整流桥总有功损耗；PBT、PBb分别为BCD 中变压器、换流器总有功损耗.

实际应用中，RU 由2 套12 脉波整流机组并联构成.每套机组均采用1 台三绕组整流变压器，其次边两绕组各连接1 个6 脉波三相整流桥，直流侧注入电流为Ibr.设各侧Ibr相等，则Ibr=Idr/4，如图4 所示.Z1T、Z2T、Z3T分别为变压器一、二次侧等效阻抗（均归算至阀侧），一般来说Z2T=Z3T，ZiT=RiT+ jXiT（i= 1, 2, 3）；Ym为变压器励磁导纳，Ym=Gm+ jBm；PL、UL分别为阀侧交流节点有功功率、线电压，如式（4）、（5）所示.

图4 12 脉波整流机组单相等值模型Fig.4 Single phase equivalent model of 12-pulse rectifier unit

式中：Pb为6 脉波三相整流桥的有功损耗；Nd为换流器桥数；kd为变压器电压变比；Xc为单桥换流电抗.

根据等值模型可计算出PRT，见式（6）.

由于二极管的总损耗近似等于其导通损耗，则Pb可近似表示为

式中：ns、np分别为三相整流桥桥臂二极管串、并联数[11]；nb为整流桥中二极管模块数；Pon为单个二极管的导通损耗，Pon=VFIFD，D为导通比，VF为正向导通压降，由二极管型号决定,IF为通态电流，IF=Idr/(ntnp) ，nt为整流桥个数.

则PRb为

BCD 中，以两模块并联的电压源型换流器（voltage source converter，VSC）为例，VSC 经两绕组变压器连接至中压网络，见图5.RT、XT、YT分别表示双向变流变压器及换流电抗器的等效电阻、电抗、励磁支路导纳（归算至阀侧），YT=GT+ jBT；Uc、θc分别为VSC 阀侧节点电压幅值、相角，Uc如式（9）所示.Ibbr为流过换流器内部的交流电流，设VSC 直流侧输出电流相等，则Ibbr=.

图5 双向变流装置单相等值模型Fig.5 Single phase equivalent model of bidirectional converter

式中：μs为直流电压利用率，与调制方式相关，空间矢量脉宽调制（space vector pulse width modulation，SVPWM）方式下，μs=1；Ms为调制度，0≤Ms≤1.

PBT如式（10）所示，PBb的有名值如式（11）所示.

式中：a、b、c为VSC 的损耗系数[12]；SN、VN分别为单个VSC 的额定容量、直流侧额定电压.

逆变时，牵引变电所供电计算模型为

式中： δs=θs-θc；Ys为BCD 等效并网导纳，|Ys|=

2.2 牵引变电所多状态切换控制策略

牵引变电所的运行状态由Ud确定，运行状态确定方法如图6 所示.

图6 牵引变电所运行状态确定法Fig.6 Method of determining traction substation operation state

实际算法中，为避免状态重复切换，保证切换的平稳性及快速性，在此基础上加入Bang-Bang 控制算法，对变量进行滞环比较，如式（16）所示[13-14].

式中：Sk为第k次迭代时变电所的状态；SL和SH分别为图6 中的相邻2 个不同状态；Ur为2 种状态之间的电压阈值，如Udl；W为滞环宽度.

2.3 牵引供电系统交直流交替迭代潮流计算

基于牵引变电所协同供电计算模型，以列车牵引计算结果及行车计划为输入，同时考虑加入滞环比较的牵引变电所状态切换控制策略，采用交直流交替迭代的方法[12]对含双向变流装置的城市轨道牵引供电系统进行求解.

3 模型验证

为验证算法的有效性及准确性，分别在城市轨道交通牵引供电仿真平台（模型1）及MATLAB Simulink 平台中搭建图7 所示的“3 所4 车”牵引供电系统模型（模型2），模拟协同供电方案下系统的运行情况.图中，MS 为主变电所，变电所TS1、TS2、TS3 分别位于457、4 000、6 000 m 处，且均设有同名车站，T1～T4 为列车.

图7 3 所4 车供电系统结构Fig.7 Power supply system structure of 3 stations and 4 vehicles

定义方案 0 为“逆变回馈装置（energy feedback system，EFS） + RU”供电方案.δV、δk分别为BCD的整流启动电压系数、下垂率系数.为方便表达，定义方案1～9 如表1 所示.

表1 Ud0 与k2 选取Tab.1 Selection of Ud0 and k2

设12 脉波整流机组额定容量为SR，降压所负载率为ηs，仿真参数及变压器铭牌参数分别见表2、3.列车为B 型车4 动2 拖编组，最高限速为120 km/h，发车间隔为200 s， 收敛精度ε= 10-3.

表2 仿真参数Tab.2 Simulation parameters

表3 变压器铭牌参数Tab.3 Nameplate parameters of transformer

图8 为方案5 下40～100 s 时间段内TS2 处直流电流、网压变化曲线，t为时间.

图8 TS2 直流电流、网压对比Fig.8 Comparison of TS2 DC and network voltage

取第116 s 时各节点电压、电流进行分析，该时刻计算收敛次数为 1 次，收敛误差为0.8×10-3，功率统计结果见表4 （此刻车载制动电阻未启动）.Pnet为直流牵引网损耗的有功功率.

表4 Pnet 与Pdevice 对比Tab.4 Comparison of Pnet and PdevicekW

图8 中，Id、Ud的Pearson 相关系数分别为0.98、0.89，表4 中，Pnet、Pdevice的最大误差百分比分别为3.5%、8.9%.由此可见，模型1 仿真结果与模型2 仿真结果基本一致，且算法收敛性较高.两个仿真结果的差别是由于模型2 中各装置特性更接近于实际情况，较于模型1 更为复杂，但两者均能基本反映供电系统潮流分布情况.

4 协同供电系统评估指标

由图2 知，协同控制策略会影响牵引变电所的外特性，进而影响直流牵引网的网压及列车功率的分配.为进一步量化协同控制策略的影响程度，现提出3 个评估指标.

4.1 直流牵引供电系统损耗

直流牵引供电系统损耗包括直流牵引网损耗、车载制动电阻吸收功率及牵引变电所运行损耗.

以图9 所示的单区间单列车牵引为例，列车等效为恒定功率源P，Ut为列车受电弓处直流网压；Rn、Rt分别为接触网、钢轨单位长度电阻，x1、x2分别为列车与相邻两变电所的相对距离；令区间长度为2 km，Req= 0.03 Ω，Rn、Rt分别为0.017 2、0.020 0 Ω/km，Pnet随Eeq、x1变化情况如图10 所示[15].

图9 单车牵引等效电路Fig.9 Equivalent circuit diagram of bicycle traction

图10 Pnet 随Eeq、x1 变化三维图Fig.10 Three-dimensional diagram of Pnet varied with Eeq and x1

由图可知，P相同时，Pnet随Eeq的升高而减小，且P越大，Pnet减小越多.当x1= 1 km，P= 4 MW，Eeq=1700 V 时，Pnet相对于Eeq= 1630 V 时减小8.67%.

由式（1）知，在限制Ud0不超过Udi的情况下，提高Ud0、减小k2，可提高Eeq，进而减小Pnet.

对于车载制动电阻，当列车处牵引网网压达到其启动电压Uon时，车载制动电阻启动，消耗多余的再生制动能量.

由式（11）可知，换流器损耗始终存在一固定分量a，其值由SN决定，对BCD 的效率影响较大.本文采用的BCD 及RU 额定工况下效率分别为97.5%、99.0%.由图1 可知，降低Ud0或增大k2，可让RU 更多地参与工作，从而提高牵引变电所总效率，减小Pdevice.

4.2 钢轨电位Urail

直流牵引供电系统中，当牵引负荷较大时，由于二极管整流机组无法有效抑制交流侧网压偏差对直流侧网压波动的影响，会出现功率越区分配过大从而导致钢轨电位异常升高[16].

由式（1）知，通过提高Ud0、减小k2，一方面可增大牵引变电所的牵引功率，减少跨区间传输的牵引功率；另一方面，可抑制直流网压波动，提高牵引网网压，从而降低钢轨电位.

4.3 考虑装置寿命期限时供电系统的综合成本

EFS/BCD 达到寿命期限时供电系统的综合成本包括EFS/BCD 的总成本及供电系统的总能耗电费两部分，如式（17）.

式中：SB、Udh、Udi、k2为各牵引变电所配置的SB、Udh、Udi、k2对应向量；SB,j为第j个牵引变电所EFS/BCD 的额定容量；cins(•) =pcSB，为EFS/BCD 安装成本，pc为单位容量成本；cmt(•)为EFS/BCD每年维护成本；Y为EFS/BCD 寿命期限的年数；WSTECy(•)为第y年供电系统的总能耗电度；Ey为第y年电价.

5 算例分析

某地铁工程线路如图11 所示，MS1、MS2 安装容量分别为2 × 40.0、2 × 31.5 MV•A，SS 为降压变电所，S1～S16 为车站，TS 为牵引所.列车为B 型车4 动2 拖编组，最高限速为100 km/h.全线各牵引变电所均设双向变流装置（两模块并联）.行车组织采用不同交路，高峰时段大交路（TS1—TS14）、小交路（TS1—TS10）发车对数分别为18、9 对/ h.

图11 某地铁工程线路Fig.11 Subway line

取方案0～3 下t= 155s时全线各节点钢轨电位、牵引网网压及牵引变电所输出功率（Pd）分布，如图12、13 所示，X为线路长度.

图12 t = 155 s 时全线钢轨电位、牵引网网压分布Fig.12 Rail potential and traction network pressure distribution when t = 155 s

图13 t = 155 s 时牵引变电所功率分布Fig.13 Power distribution of traction substation when t = 155 s

与方案0 相比，BCD 参与整流时，部分牵引变电所Pd增加，从而减少了跨区间传输的牵引功率；牵引网网压上升，上行钢轨电位最大值降低12.6%～15.6%，下行钢轨电位最大值降低14.7%～17.5%.当k2= 3%，Ud0= 1 700 V 时，牵引网网压水平最高，随着Ud0的降低，牵引网网压呈下降趋势，钢轨电位略有上升，但变化不大.因此，提高Ud0可以提高牵引网网压水平，但对于改善钢轨电位效果不明显.

与方案1、2 相比，方案3 策略下，TS11、TS13处网压明显升高，逆变功率大幅上升.据统计，仿真周期内方案1～9 全线钢轨电位的最大绝对值分布范围为113.19～116.06 V.由此可知，改变k2对钢轨电位影响较小，这是因为Req始终受到k1、k2中较小值的限制，变化范围较小.

图14 为算例工程平均每小时的直流牵引供电系统损耗电度WDCLOSS，图中，Wres、Wdevice、Wnet分别为车载制动电阻吸收的有功电度、牵引变电所运行损耗的有功电度、直流牵引网损耗的有功电度.

图14 直流牵引供电系统平均每小时损耗电能Fig.14 Average hourly power loss of DC traction power supply system

由图14 可知，k2一定时，WDCLOSS随Ud0的增大，先升高后降低.这是因为，Ud0较小时，直流网压水平较低，线路中制动列车产生的再生制动能量优先通过牵引网被相邻牵引列车吸收；随着Ud0增大，直流网压水平上升，Wnet减小，而由于双向变流装置更多地参与整流，Wdevice增加，同时车载制动电阻启动频率增加，Wres增加；当Ud0继续增大时，直流网压水平进一步升高，此时多余的再生制动能量优先被双向变流装置回馈至交流供电系统，同时车载制动电阻启动频率降低，Wres减小.对比方案1、4、7 可知，Ud0一定时，k2变化对WDCLOSS影响较小.

与方案0 相比，双向变流装置参与整流后，方案3、6、9 下的WDCLOSS明显降低，其中方案6 下的WDCLOSS下降约9.7%.

对算例工程进行分析，发车计划及详细参数见表5、6，其中，初、近期运营时间分别为3、7 年，综合成本如表7 所示.

表5 工程算例行车组织Tab.5 Traffic organization of cases

表6 综合成本参数Tab.6 Overall cost parameters

由表7 可知：方案3、6、9 的综合成本相比方案0 分别减少了0.30%、1.17%、0.89%，即265.25、1 034.11、788.06 万元；而对于方案1、2、4、5、7、8，综合成本均高于方案0.这说明相比方案0，在协同供电方案下，当适当提高Ud0时，可节省双向变流装置到达寿命期限时供电系统的综合成本.

6 结 论

1） 本文给出了协同供电方案下牵引变电所的综合输出外特性及直流等效电路模型，提出了考虑滞环比较的多状态切换策略，实现了含双向变流装置的城市轨道牵引供电系统协同供电潮流计算；并通过Simulink 仿真结果，验证了算法的有效性及准确性.

2） 协同供电时，部分牵引变电所输出的牵引功率增大，牵引列车从邻近牵引变电所吸收能量，跨区间传输的牵引功率减少；牵引网网压上升，全线钢轨电位最大绝对值降低.k2为3%时，算例工程全线上、下行钢轨电位最大值分别降低12.6%～15.6%，14.7%～17.5%.提高Ud0可提高牵引网网压及部分牵引变电所的逆变功率，但钢轨电位变化不大；改变k2对网压及钢轨电位的影响较小.

3）Udi一定时，随着Ud0的增大，WDCLOSS先升高后降低.与方案0 相比，Ud0为1 700 V 时，算例工程的WDCLOSS明显降低，最多降低9.7%，综合成本最多降低1.17%.k2变化对WDCLOSS影响较小.对于直流牵引供电系统，Udi一定时，适当提高Ud0可以获得更佳的节能效果.