进料浓度对模拟移动床雌马酚对映体分离效能的影响

苏木玲，余卫芳，张璐，李志雄

（温州大学 化学与材料工程学院， 浙江 温州 325035）

色谱的诞生由来已久，其初次发明并使用在20年代初期，Mikhail Tswet 用碳酸钙作为吸附剂，二硫化碳作为洗脱剂，将植物色素（叶绿素和叶黄素）进行色彩分离，并在其发表的论文将其命名为“Chromatography”,即色谱。与其他分离方法相比，色谱法具有选择性高、分离效率好、产品纯度高和操作成本低等优点，在石油化工[1]、医药行业[2,3]、生物工程[4]、精细化工和食品行业[5]应用极为广泛。特别是在手性药物拆分方面，色谱技术尤其是模拟移动床（Simulated Moving bed, 简称SMB）色谱分离技术的应用越来越受到广泛关注。

模拟移动床是一种基于色谱分离原理为基础的分离技术，最初起源于于石油行业，由美国环球油品公司（UOP）提出并应用于分离对二甲苯。与间歇式色谱相比，模拟移动床技术因其具有连续性、固定相利用率高、溶剂消耗少且生产率高等优点，在石油化工、制药工业和制糖工业应用极为广泛[6-7]。

雌马酚（equol）是大豆异黄酮的产物，在抗氧化性和雌激素活性方面优于大豆异黄酮[8]。雌马酚作为对映异构体，存在R-和S-型两种形式，这两种雌马酚对映体功能不同，应用也不同。从多种动植物产品[9]中可获得各种光学纯度的马酚，但其生产效率有限。化学合成是满足日益增长的市场需求的一种替代方法。虽然文献[10]报道了不对称合成，但据我们所知，化学法生产的马酚主要以外消旋体形式存在。因此，研究马酚对映体的高效分离具有重要意义。

本研究目的是采用模拟移动床系统，在最大消旋体浓度条件下，选取一定比例作为SMB 进料浓度，对雌马酚对映体进行多目标优化，探索SMB 系统最佳的生产性能。

1 理论部分

1.1 数学模型

本文采用平衡扩散模型（equilibrium dispersive model,ED）模型对SMB 柱内进行物料衡算,模型参数由罗云等测量[11]。该模型具有以下形式：

式中c和q分别为流动相浓度和固定相浓度（单位为mg mL-1），t 是以min 为单位的时间，F 是与柱空隙率有关的相率，表示为，uj为流动相间的线速度，z 是以 cm 为单位的轴向坐标，在固相体积上，Dapp是集合分子扩散、涡流扩散和传质影响的表观轴扩散系数，i（A 和B）和j（I，II，III 和IV）分别表示组分数和色谱柱所在区域。等式(1)需要补充二元吸附等温线来完成。Bi-Langmuir 模型广泛应用于对映体[12]的竞争吸附，已被证明适用于马酚对映体：

为简洁起见，在Eq(2)中省略了色谱柱所在区域j。Bi-Langmuir 模型有5 个参数:非选择性和选择性位点的饱和容量(qns,qs)，平衡常数(bns,bs,A,bs,B)。在雌马酚吸附的情况下，根据线性溶剂强度(LSS)模型[11]，可以假设饱和容量是恒定的，而平衡常数取决于流动相组成。

求解式（1）需要特定的初始条件和边界条件，在SMB 工艺开始时，进料在进料口处被纯溶剂取代。在每个切换结束时，端口位置沿流动相方向进行切换，如图1 所示，可通过每次切换时间开始时更新柱内的初始条件和边界条件来体现这些。因此，初始条件和边界条件如下所示：

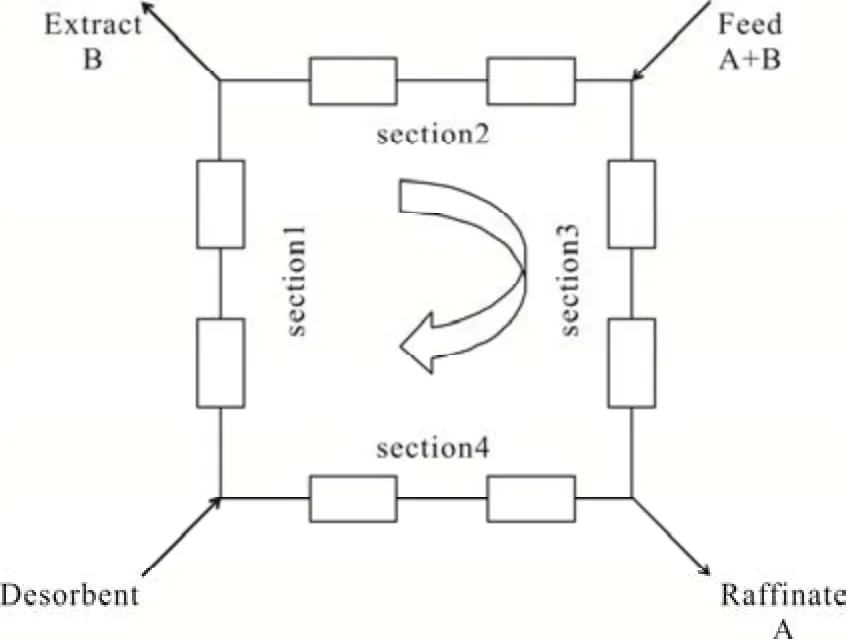
图1 4 区八柱示意图

1.2 节点模型

图1显示了本文研究中应用的SMB 系统的示意图。它由四个区组成，每个区含有两个色谱柱。各区进出口对应的节点平衡[13-14]如下：

洗脱液节点：

萃取液节点：

进料液节点：

萃余液节点：

1.3 模型参数

表1 的参数值是根据先前出版物中流动相配比为0.4 时，进料浓度按照文章中最大消旋体浓度的90%进行计算，最大流量按照压降关系式得出，该值与以往研究值保持一致[11]。

表1 模型参数

2 SMB 的多目标优化

2.1 变量定义

本文中以轻重组分作为约束条件，研究了轻组分的纯度和单位产率作为优化目标函数。为了评估SMB 分离雌马酚过程的体现，展开更为深入的讨论，定义以下SMB 的函数：

j区液固流量比：

S-雌马酚纯度：

R-雌马酚纯度：

单位产率：

2.2 优化问题描述

在接下来的讨论中，两个同时被优化。由于变量对目标的影响是相互矛盾的，因此通常会获得一组被认为等效的求解点，称为“非劣解”。 非劣解集合意味着当我们从任何一点到另一点时，至少一个目标函数变得更好而至少一个恶化。因此，在pareto 集合中的任何点都是最优的并且可以接受[15-16]。

理论上，SMB 可能有许多多目标优化配置。本文共研究了一个具有实际意义的问题，即纯度和单位产量同时最大化。将4 个独立的操作参数mⅠ、mⅡ、mⅢ、mⅣ作为决策变量。在SMB 温度固定在298 K 条件下，选取最大消旋体进料浓度c 的0.2、0.4、0.6、0.8 和1.0 倍作为进料浓度，如表2 所示。

表2 优化问题描述

本研究所有结果应用非支配排序遗传算法(NSGA-II)[17]得到非劣解。表2 还提供了使用NSGA所需的关键参数。所有计算都用FORTRAN 代码编程。

3 结果与讨论

在这项研究中，纯度PurA 和单位产率UT 同时最大化，这是中小企业研究中最关注的的优化问题之一。除了这两个目标外，还将两个组分纯度限制在0.95～0.995 之间，缩小了在实际范围内寻找最优操作条件。

PurA 和UT 同时最大化的非劣解图见图2。该图显示，从左至右PurA 上升而UT 下降，呈现如前所述的冲突趋势。根据式（10）可知，单位产率UT与总进料浓度cTF乘以(mIII-mII)的乘积成正比，与（mI+1/F）成反比关系。

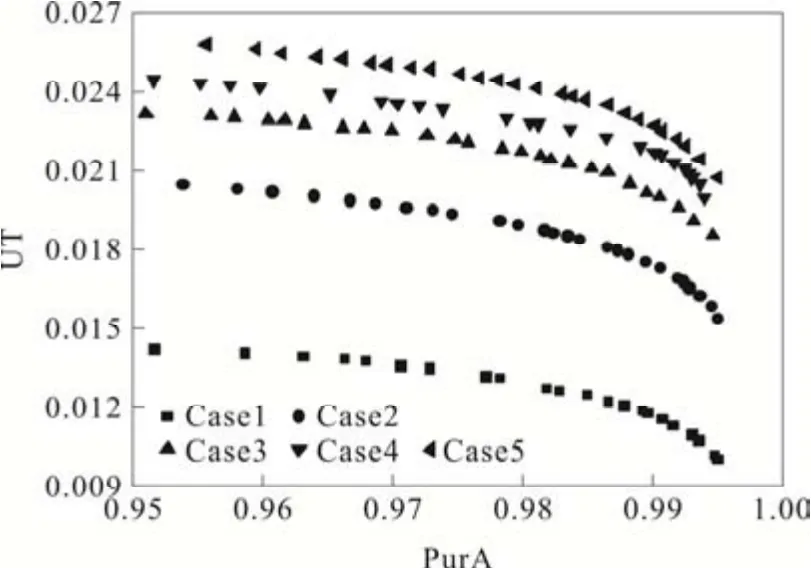
图2 UT 和PurA 同时最大化对应的非劣解图

图3a-c 显示，PurA 增加时UT 减小的原因受mI、mII和mIII的综合影响，但是5 个案例下的m1值差异较小，对于整个优化过程不起决定性作用，但该流量要足够大才能有效洗脱强吸附组分，确保固定相吸附剂的再生。mIV呈现不规则的趋势(图3d)，不规则分布但总体上要小于某一特定数值，对应在IV 区能够充分再生洗脱剂的最大流量。

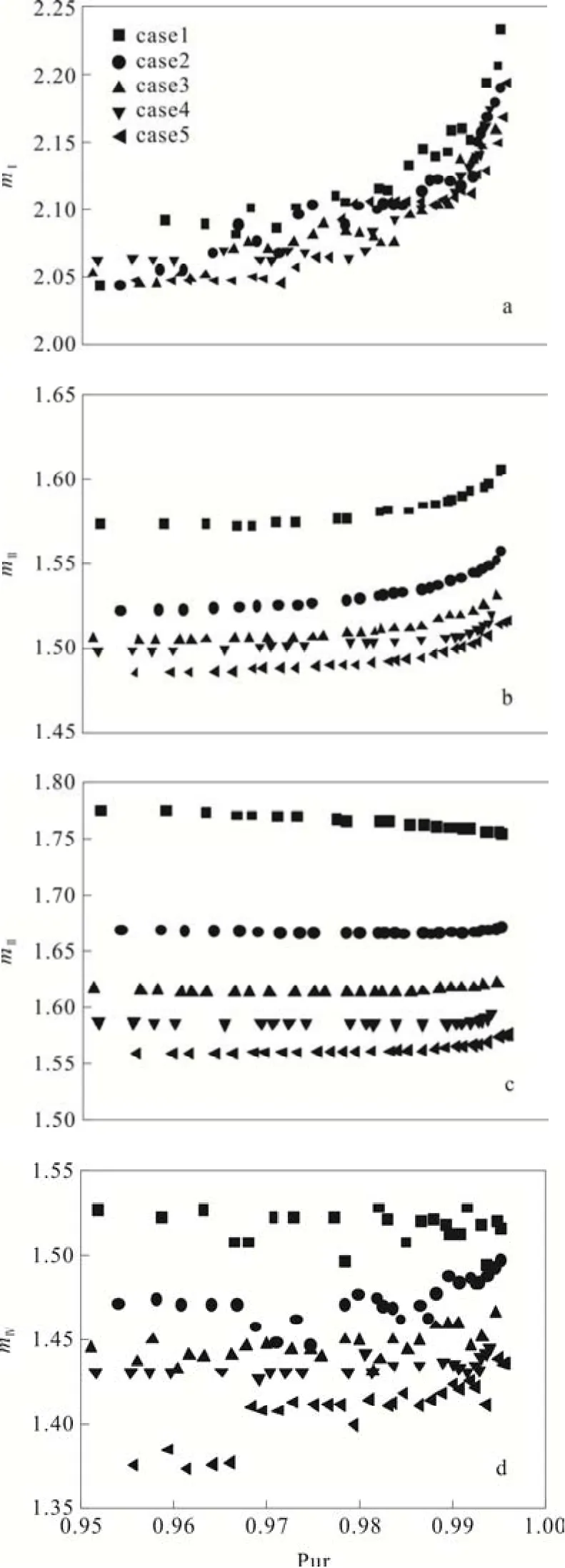
图3 UT 和PurA 同时最大化对应的最优m 值

将图2 的非劣解与图3b-c 中mII和mIII最优值分布比较可知，mII和mIII是非劣解的决定变量。再结合图3b-c 的m值和值可得，在值增加和减小的综合情况下，最大单位产率随值增加而增加[18-19]。而对于图3c 中自case2 至case5 的mIII值在纯度大于0.99 后却增加的情况，该解释为：根据三角形理论，在较低纯度时三角形域可操作性区域较大，而随着纯度增加时，操作点远离对角线，所以在满足完全分离的条件下，意味着进料流量有增加的趋势，故mIII的值在高纯度时会出现增大的趋势[20]。

4 结 论

本文以雌马酚对映体作为模型体系，基于多目标优化结果评价了5 种进料浓度cTF的设置对SMB生产性能的影响。本文就PurA 和UT 同时最大化的问题进行了研究。优化结果表明SMB 设计操作对PurA 和UT 的影响是相互冲突的，即存在一系列的非劣解。I 区的流量比mI对SMB 的影响在于保证固定相的再生。在整个优化过程中，(mIII-mII)和cTF是直接决定非劣解趋势的关键变量，优化后(mIII-mII)的随UT 的增加而增加。总进料浓度cTF对非劣解显著影响在于，在相同的产品纯度要求下，较高cTF的值可以实现更高的单位产率。