基于人工神经网络的高效电磁诱导透明超表面阵列设计

院琳，唐佳，于海洋，张城

（西南电子设备研究所，四川成都 610036）

1 引言

电磁诱导透明（Electromagnetic Induced Transparent，EIT）是通过利用三能级原子系统中的量子相消干涉，从而在宽吸收光谱上产生极窄带的透明窗口［1］。研究表明，通过合理设计超材料［2］的单元结构，可以实现主动可调的EIT效应［3］。

传统的超表面设计方法通常是基于人的直觉和工作经验。为了验证设计指标是否实现，需根据所设计的超表面结构，计算出相应电磁响应。电磁响应的获取依赖于广义理论分析方法或数值计算方法，如有限元法（Finite Element Method，FEM）［4］、时域有限差分法（Finite-Difference Time-Domain，FDTD）［5］来预测。这种传统的设计方法不仅是建立在试错的基础上，更需要丰富的工作经验和时间对多维空间中的物理或几何参数进行调整使其满足指标要求。随着超表面结构的日益复杂，该设计方法的局限性逐渐显现出来。因此，能够根据目标的电磁响应快速确定相应结构的物理或几何参数，尽可能减少人为干预程度的超表面设计方法具有重要的研究意义。

人工神经网络［6］（Artificial Neural Network，ANN）是一种受人脑生物神经元启发的信息处理系统。基于简单的数学工具和海量的分布式并行信息处理，通过自动化的训练过程，神经网络可以表征输入和输出之间的多维非线性关系，得到良好训练的神经网络能够根据输入提供非常准确和快速的输出预测。考虑到神经网络的优良特性，为了简化电磁器件的设计流程，减少对设计师经验的依赖，近年来，基于人工神经网络的软计算方法被广泛用于电磁器件的建模与设计中，如滤波器［7］、微波功率放大器［8］、超表面［9］等。一旦建立了模型，就能根据目标电磁响应，快速获取满足需求的物理或几何参数，且可以被重复使用［10］。但目前，针对EIT超表面阵列设计，基于神经网络模型的软计算方法研究还相对较少。此外，考虑到EIT超表面阵列往往工作在太赫兹［11］及更高频段，具有频带范围宽的特点，将离散电磁响应作为神经网络模型的输入将会使模型结构复杂，导致训练难度大。为此，本文提出了一种结合传递函数（transfer function）与神经网络的模型，用于EIT超表面设计。采用基于传递函数的矢量拟合技术，对电磁响应进行拟合处理，提取传递函数的极点与留数，并将其作为神经网络的输入。EIT超表面阵列的几何参数作为输出。该方法可有效降低神经网络的结构复杂度，训练好的神经网络可根据所需电磁响应快速输出相应EIT超表面阵列几何参数。以一个基于高低谐振环结构的EIT超表面为例，证明了提出方法的有效性。

2 提出模型

2.1 基于传递函数的矢量拟合

由于EIT超表面工作在太赫兹及更高频率，因此其具有较宽的工作带宽，若采用离散法对电磁响应进行良好表征，则会导致数据维度过大。为了降低数据维度，利用基于极点与留数的传递函数来表示电磁响应T与频率f的关系［1］。基于极点和留数的传递函数如式（1）：

其中，s=jω，ω=2πf，N表示传递函数的阶数，pk和rk分别称为传递函数的极点和留数。通过矢量拟合提取极点和留数，并将其馈送到神经网络中。

2.2 模型架构

所提出的模型（以下简称“提出模型”）结构如图1所示。第一层是输入层。相比采用离散电磁响应作为输入的神经网络模型，提出模型的输入将采用矢量拟合技术提取传递函数的极点和留数。模型的第二层为隐藏层，隐藏层神经元个数i采用Hecht-Nelson方法确定，即

图1 提出的基于传递函数神经网络模型

其中，m为神经网络输入层神经元个数。第三层为输出层，将产生满足EIT超表面所需的几何参数。

2.3 样本获取

以一个基于高低谐振环结构的EIT超表面［13］为算例验证提出模型的有效性。该EIT超表面如图2所示。

图2 高低谐振环超表面阵列结构

基于高低谐振环的EIT超表面阵列，考虑到其透射谱是重要的电磁特性，阵列的单元间距、单元内环高度、外环高度都对其有显著影响，因此，以透射谱为目标电磁响应，利用提出神经网络模型获取相应单元间距、单元内环高度、外环高度三个几何参数。

为了生成训练和测试样本，使用CST Studio Suite 2019软件进行全波电磁仿真，获取了130个训练样本数据以及50个测试样本数据。

2.4 建模结果

为了对神经网络模型进行训练，首先利用矢量拟合技术提取训练样本透射谱所对应的极点与留数，将其作为训练样本的输入。为了精确表征透射谱特征，采用10阶传递函数，提取极点和留数各10个，馈入到所提出的神经网络模型中，作为输入。相比对电磁响应采取离散处理的方法，采用极点和留数的传递函数进行表征，极大的减少了神经网络的输入个数，从而降低了神经网络结构的复杂度。单元间距、单元内环高度、外环高度三个几何参数作为神经网络输出。在训练过程中，Logsigmoid函数作为隐藏层神经元激活函数，并采用Levenberg-Marquardt训练算法。根据Hecht-Nelson方法计算，41个神经元组成隐藏层。训练过程如图3所示。经过训练过程，提出的模型能够根据目标透射谱生成相应几何参数。为了验证提出模型的泛化性，利用测试样本对训练好的提出模型进行测试。测试流程如图4所示。在训练和测试过程之后，为了量化所提出神经网络模型的性能，使用平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）来评估准确率。具体的数学表达式如下：

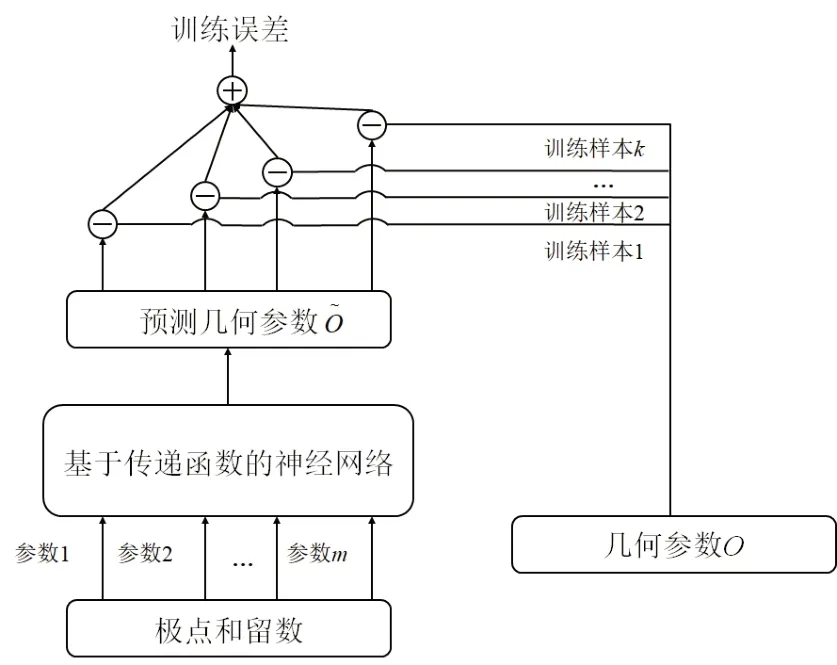
图3 提出模型训练流程

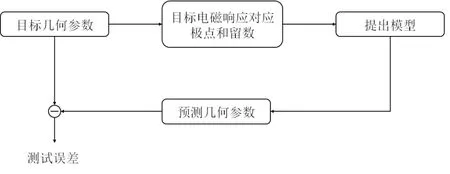
图4 提出模型测试流程

其中，n为样本个数，Ok为神经网络目标输出为神经网络实际输出。结果如表1所示。提出的神经网络模型的训练和测试误差分别为5.58%和6.60%，表明提出模型得到了较好训练且具有不错的泛化性。

为了比较，将采用等间隔频率离散后的透射谱作为输入，直接馈入神经网络模型中。此时神经网络的输入维度为250，因此根据Hecht-Nelson方法确定需501个隐藏层神经元。该模型相比提出模型具有更加庞杂的网络结构。同样采用Logsigmoid函数作为基于离散透射谱的神经网络隐藏层激活函数。在训练过程中，依然采用与提出模型一致的Levenberg-Marquardt训练算法。经过训练后，该模型的性能如表1。训练误差为14.59%，测试误差为17.19%。

通过对比发现，本文提出的神经网络模型基于传递函数对透射谱进行拟合，将极点和留数代替等间隔频率离散的透射谱，可以将神经网络模型的输入维度由250降低到20，并减少隐藏层神经元数量，由501降低为41。由于简化了网络模型结构，从而降低了神经网络模型内部的权值与阈值数量，有利于在小训练样本数量的条件下，获得更好的训练，具有更好的性能。

为了进一步验证提出模型的有效性，根据目标电磁响应，利用提出模型获取所需几何参数。希望利用该模型获得满足在0.52—0.54 THz频带内透射系数达到0.65的EIT超表面几何参数。将电磁响应所对应极点和留数输入神经网络模型，获得几何参数如下：

通过CST软件计算该预测几何参数所对应EIT超表面结构的透射光谱，如图5所示。由图可见，获得的电磁响应在频率0.52 THz与0.54 THz的透射率，分别达到0.672 61与0.700 01，并在0.52—0.54 THz频带内透射系数都达到0.65。通过对比根据提出模型获得的几何参数相应透射谱与目标透射谱，该结构较好地满足了设计目标。

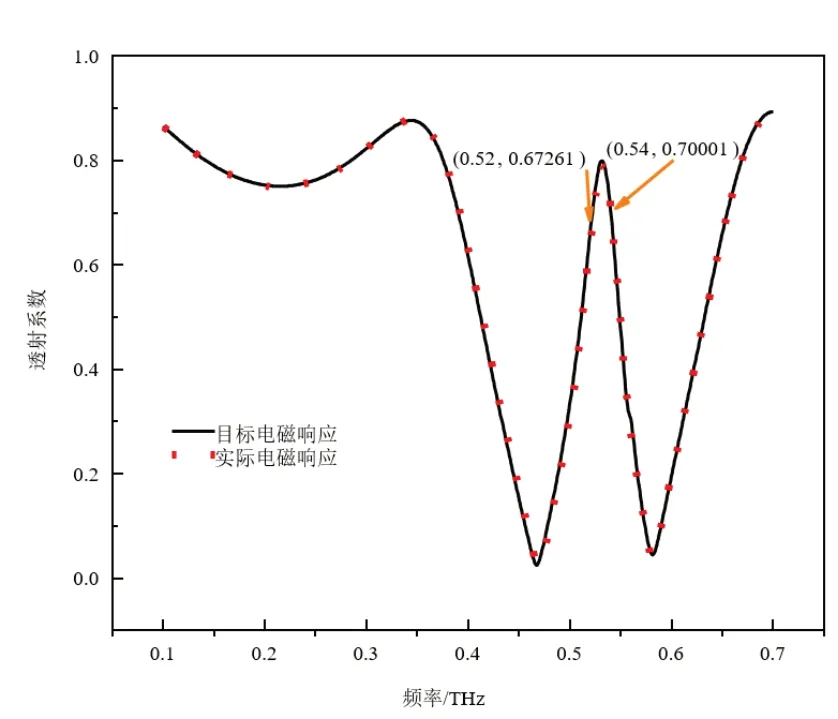
图5 提出模型获取几何参数对应电磁响应与目标电磁响应对比

3 结论

EIT超表面因其独特的性质，近年来得到了广泛研究。由于基于数值仿真的EIT超表面阵列设计方法所需计算资源大，提出了一种基于神经网络模型高效EIT超表面阵列设计的方法。提出模型旨在根据目标的电磁响应特性，确定超表面的几何参数。借助基于极点和留数的传递函数对电磁响应进行表征，显著降低了神经网络模型的输入维度，简化了网络结构。在完成良好训练后，只需输入所需的电磁响应，提出模型就可以快速输出满足要求的几何参数。以一个基于高低谐振环的EIT超表面阵列为例，验证了提出模型的有效性。这种设计方法也可应用于其他微波或光学器件。