12C16O精确的半经验势能面、 振转光谱及温度压强效应研究

陈恒杰, 方 旺, 张家伟

重庆科技学院数理与大数据学院, 重庆 401331

引 言

CO广泛存在于宇宙, 是大气中最广泛的污染物之一, 也是非常好的示踪分子, 还是各高温燃烧过程的重要产物, 其精确的谱线位置、 谱线强度等光谱参数, 对包括天体物理、 环境检测、 燃烧诊断在内的科研、 国防及工程领域具有十分重要的意义, 使其长期占据研究热点。 常温下12C16O的振转光谱已被大量报道, Coxon等及后来者对此做过详细总结[1]。 近年,12C16O的多个新泛频带被先后报道, 如: Tan等在296 K温度下, 首次对0-6振动带的32条转动跃迁进行了观测, 这是截止目前实验上获得的最大倍频带[2]; Postorek等采用时间分辩傅里叶变换红外发射谱(FTIR)对12C16O基态直到ν=30, 且Δν=1, 2的多个带进行了研究[3]。 尽管实验技术有了长足进步, 但对高振动态、 高转动态, 因其强度弱, 辐射寿命短, 同时受制于仪器灵敏度、 噪声等影响, 实验探测依然是一项挑战, 要想从实验上获得全波段任意温度任意压强下的振转光谱更是不可能完成的任务。 而另一方面, 基于振转光谱测温的现实, 急迫需要大量的、 精确的基础光谱数据以及其随温度的变化情况。 原则上, 严格的理论计算能获得直到解离极限的绝大多数光谱信息, 在实践中发挥了重要作用[4], 然而即便对低振动态的能级, 理论结果与实验值也存在较大差异, 在高振动态差异则更加明显[5]。 因此, 如何基于有限的实验数据, 建立一个高精度、 高分辨、 全局的解析势函数, 不仅可以完善分子振转光谱全貌; 还可结合偶极矩函数研究振转光谱随温度、 压强的变化, 对构建振转光谱测温测压模型有重要指导作用。

本文首先构建了CO基态精确的半经验全局势函数, 接着基于差分技术获得偶极矩面, 然后系统研究了12C16O的振转光谱, 分析其随温度的变化情况, 提出若干测温思路, 最后探讨了压强对振转光谱的影响。

1 计算方法

1.1 势能面

通过Farrenq等利用ATOMS傅里叶变换光谱仪, 基于基带和第一倍频带决定的旋转常数Bν和振动常数Gν[6], 依据Rydberg-Klein-Rees (RKR)反演方法, 产生了最大和最小核间距经典转换点Rmin和Rmax, 以及J=0时的振动能级E(ν), 在ν<41时,E(ν)与文献结果几乎一致[1], 将ν<41的转换点和E(ν)拟合到十多个常见的解析势能函数, 依据确定系数(R-Square)和均方根误差(RMSE)优选出拟合效果最佳的两种形式, 分别为SPF和Morse函数。 为了将势函数拓展至完全解离极限, 对长程上具有连续光滑特性的Morse函数进行修正, 最初的Morse势函数被修正到全局形式, 用Revised-Morse表示。

式中,y=1-e-a0(r-re)。

1.2 偶极矩面

偶极面是计算振子强度, 模拟振转光谱的基础, 多个文献报道显示, 针对CO, ACPF结合有限差分获得的偶极矩更加可靠, 鉴于此, 本文使用 ACPF方法结合有限差分技术得到CO的偶极矩面(DMs)。 计算时, 分别考虑了外加电场E=±0.005、 ±0.000 5、 ±0.000 1 a.u三种情况。

1.3 常温下的振转光谱

结合Revised-Morse势和上述DMs, 通过求解一维薛定谔方程

(1)

得到CO在常温下直到解离极限的振转能级、 离心畸变常数、 振动跃迁偶极矩、 爱因斯坦系数、 辐射寿命、 谱线强度等光谱参数。 其中:

振动态的爱因斯坦系数,

(2)

在此基础之上, 获得的辐射寿命和谱线强度分别为

(3)

(4)

1.4 高温高压下的振转光谱模拟

通过考察不同温度下的配分函数得到任意温度下的谱线强度, 将上述谱线在不同温度和压强下按一定的线型和分辨率展宽后, 最终获得具有一定轮廓、 与实验可比的光谱图。

(5)

2 结果与讨论

2.1 势能面

基于RKR反演获得的(ν<41)的核间距和振动能级数据, 将其无约束拟合到Morse解析势函数, 拟合误差见图1。 可以看出,n=15时, 在低振动能级上Morse函数的拟合误差均小于0.05 cm-1, 在高振动能级上, 误差也保持在0.1 cm-1以下, 在合理误差范围内再现了实验振动能级。 尽管在ν≤41时, 拟合的势函数性能优异, 但仅从数学上尽可能降低RMSE, 未考虑实际物理意义, 拟合的De为105 048 cm-1, 严重偏离了实验值90 674 cm-1[7], 可以预见, 当ν>41时, 由该函数预期的振动能级必然偏离真实值。 鉴于此, 我们将De固定到90 674 cm-1, 导致整体上拟合的RMSE和误差轻微增大, 但函数具有了合理的解离极限, 整体上更符合物理实际, 拟合结果见表1。 即便如此, 也不能保证在ν>41的长程上有很好的渐进趋势。 为了检验, 我们利用多参考组态相互作用(MRCI)理论在不同活性空间和基组下进行了大量计算, 扫描了相关理论水平下的势能曲线, 图2展示了RKR, MRCI和Morse结果, 可以看出, 在解离极限附近, Revised-Morse的势能曲线与MRCI(3, 0, 0, 0)/(6, 2, 2, 0) AV5Z-DK3获得的势能曲线非常接近, MRCI得到的解离能为90 717 cm-1, 与实验值90 674 cm-1非常接近, 差异仅有43 cm-1, 间接说明了Revised-Morse在长程上是可靠的, 为了进一步检查, 基于该解析函数求解包含振转项的薛定谔方程, 得到J=0时的振动能级见表2, 可以看出, 在ν<41时, Revised-Morse得到的振动能级与Coxon和孙卫国等利用代数方法(AM)得到的结果几乎一致, 在ν>41时, 当前结果与AM预测的结果也很符合[8], 随着ν进一步增大, 两者的差异略有增加, 孙卫国等共得到了78个能级, 本文预测有80个能级, 在接近解离极限时, 两者同一能级相差约100 cm-1, 但最终达到同一解离极限, 反映出在局部范围内本文的预测是合理的, 当前Revised-Morse势是一个全新的、 可行的全局解析势函势, 对于预测12C16O振动能级ν略大于41的振转光谱比较可靠, 对精确预测更高长程上的振转能级还需要进一步校正, 对研究化学反应的解离现象十分可靠。

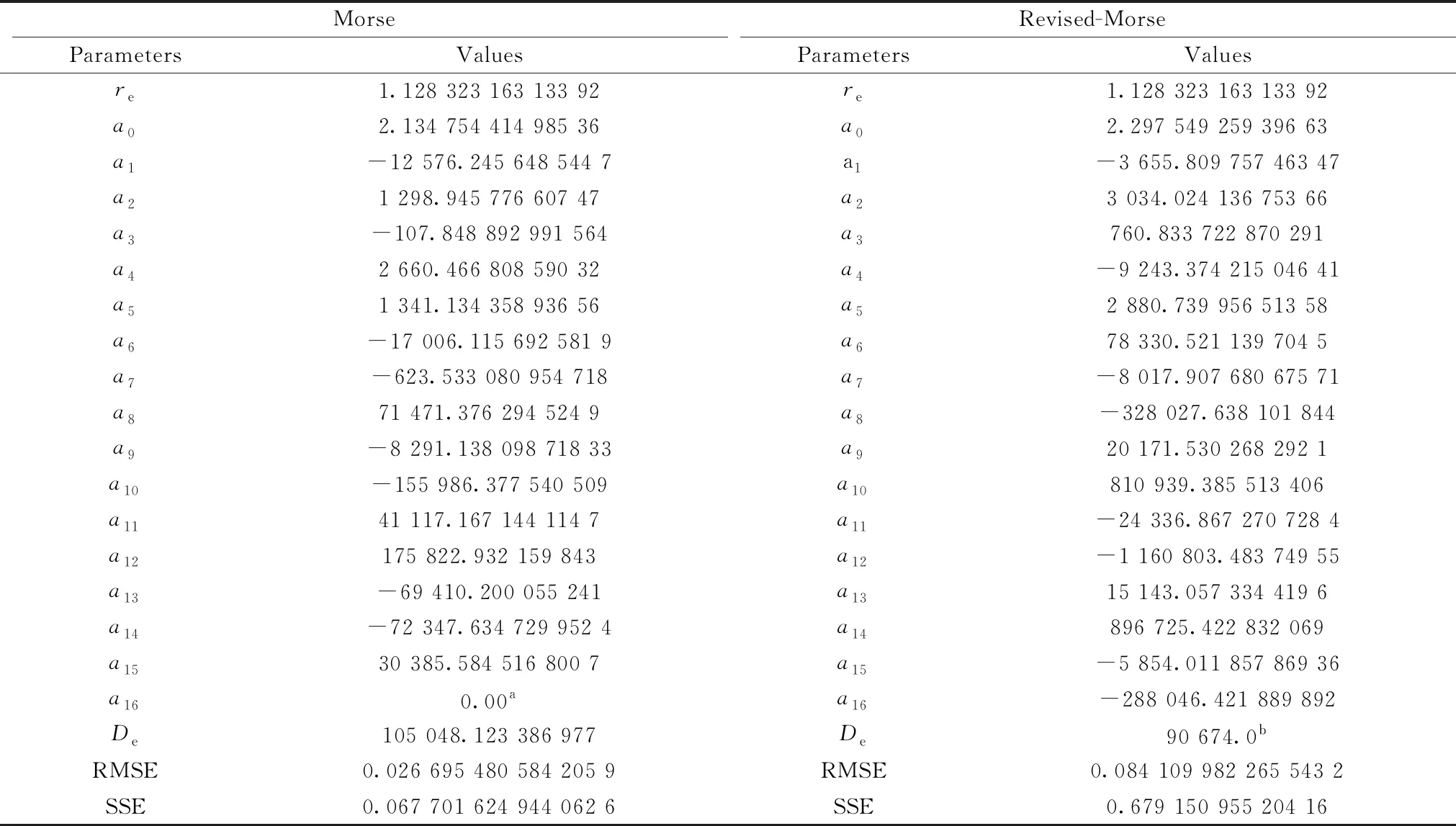
表1 12C16O的Morse和Revised-Morse势函数参数

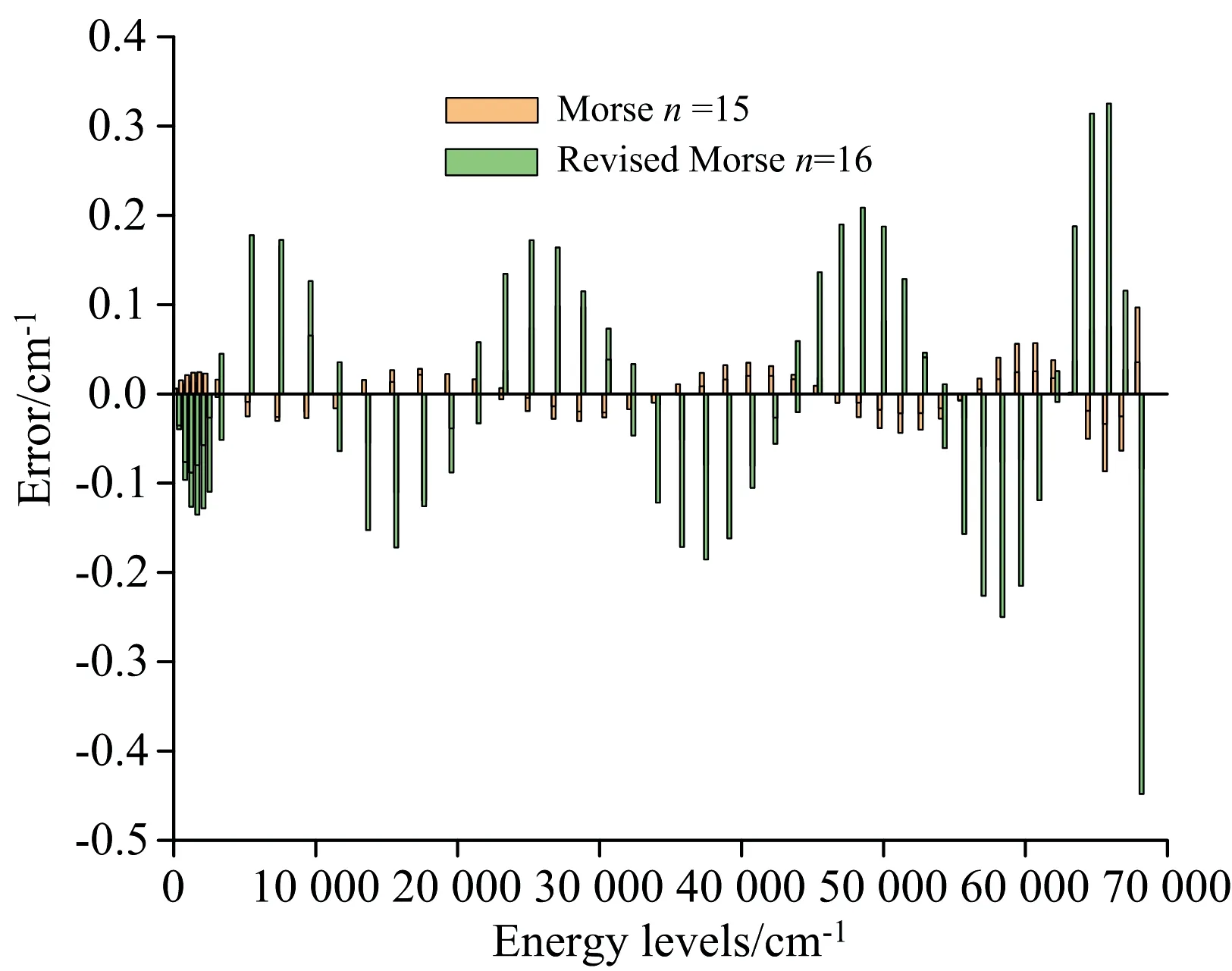
图1 Morse, Revised-Morse函数拟合误差

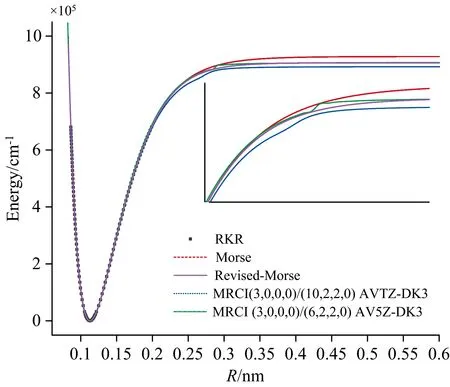
图2 势能函数图

图3给出了本文计算的直到ν=62的偶极矩, 多个文献结果也被一并列入比较, 由图可见, Kiriyama和Sidney的偶极矩在长程上发散, 其他文献结果和当前计算都有个极点存在, 在冻结核近似下, 利用CCSD(T)/AVTZ计算得到的偶极矩极点明显偏小于其他结果, MRCI、 考虑核价关联后CCSD(T)/ACV5Z以及ACPF结合有限差分计算的偶极矩相近, 各核间距下, 利用ACPF结合三种外电场下获得的偶极矩差异较小。

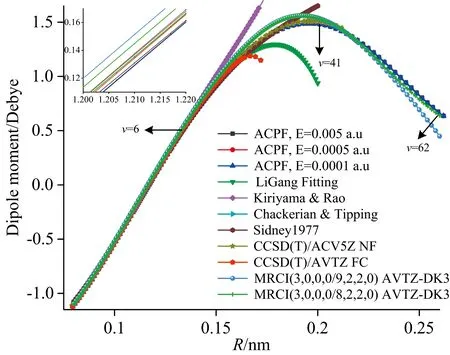
图3 偶极矩函数

基于上述分析, 我们用Revised-Morse势和E=0.000 5 a.u下获得偶极矩, 求解了包含振转项的一维薛定谔方程, 得到了直到解离极限的所有光谱跃迁线共八十多万条, 同时获得了ν<63时的线强, 在此基础上大量光谱参数也被获得, 鉴于篇幅限制, 这里不再一一列出。 截止目前, HITRAN数据库收录的最大谱线位置为14 477 cm-1共1 344条谱线, HITEMP将其扩展到22 149 cm-1, 针对12C16O也仅有19 119条, 本文报道了大量新的谱线。 作为示例, 图4给出了1个大气压下, 温度为296 K时12C16O基带谱线位置与强度的关系, 显然, 当前工作完美再现了HITRAN数据库中的P支和R支, R支的强度整体上略大于P支, 但峰宽略窄; 两支的最大强度谱线与HITRAN结果完全吻合, 当前计算的谱线强度整体上轻微大于HITRAN结果, 特别在J值较大的位置, 但两支均形成光滑的包络面, 对利用振转光谱双线测温影响不大。

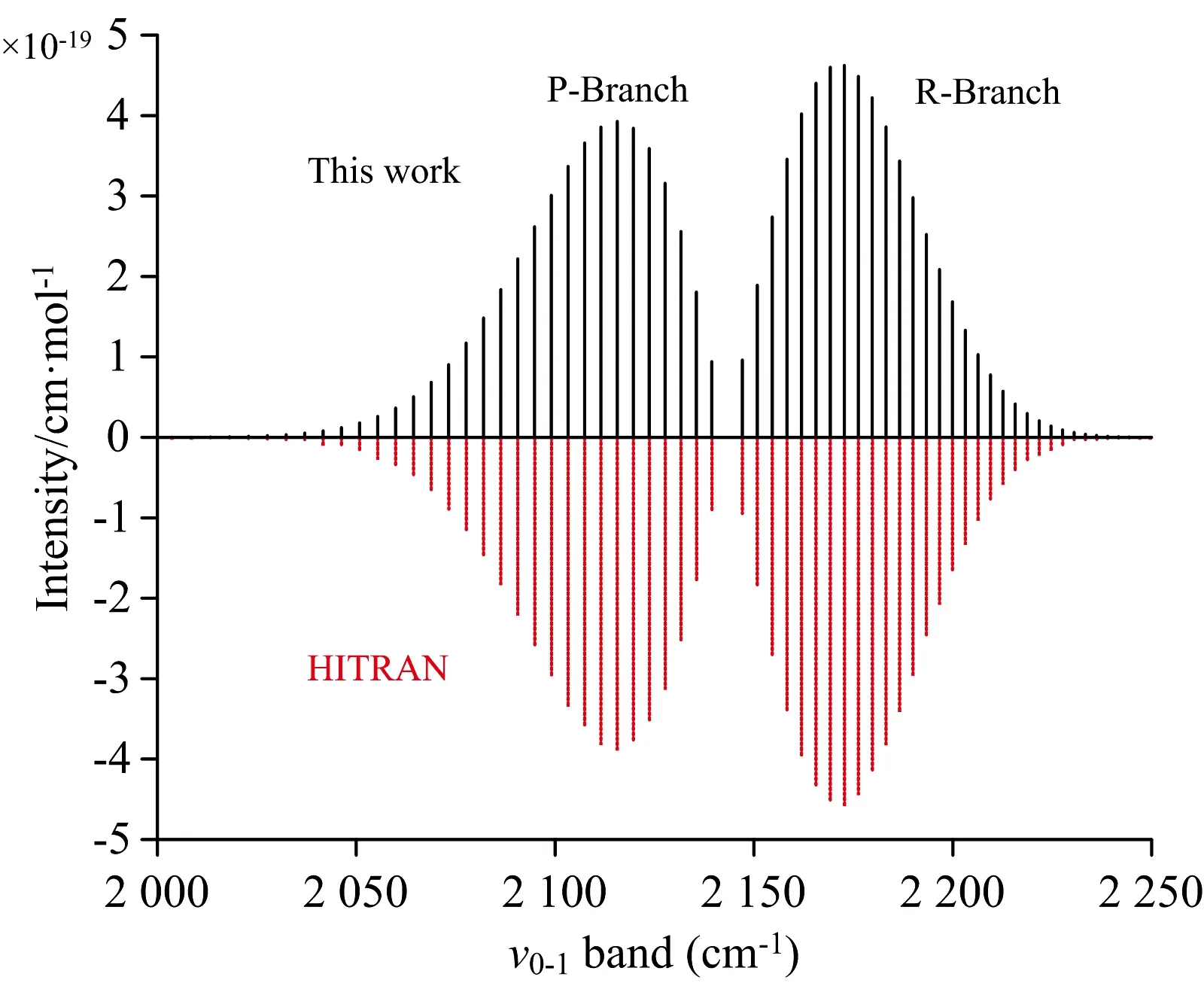
图4 计算的ν0-1带与HITRAN结果比较(1P, 296 K)

图5显示了对数坐标下Δν=1的多个带, 当前计算结果与现有的 HITRAN结果完全吻合, 一系列新的带(如:ν3-4,ν4-5,ν5-6, …)也被一并获得。 可以看出, 随着ν的增大, 带的整体强度呈级数减小, 且ν每增加一, 相应的带强下降约4～6个数量级, 另外, 谱带积分面积减小, 带头逐渐向低波数偏移。

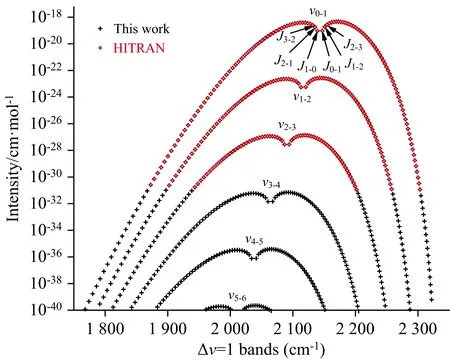
图5 Δν=1时计算的振转谱与HITRAN比较(1P, 296 K)

截止目前, 实验已观测最大Δν为ν0-6振转谱带, 为了检查泛频带的计算结果, 表3列出了ν0-6倍频带的跃迁能(E)、 爱因斯坦系数(A)和谱线强度(f), 同时HITRAN和CRDS结果也被一并列入比较[2]。 可以看出, 由Revised-Morse得到的20个P支和20个R支跃迁能级, 与HITRAN和CRDS两者的差异都在0.1 cm-1以下, 在J较大的P支完全可以转动分辨, 即便在跃迁能相差较小的R支的较大J(如J=19, 20) 处, 当前结果仍具有很好的转动分辩, 充分说明在Δν相差较大的高波段处, 由Revised-Morse势函数计算的振转跃迁能级是值得信赖的。 无论HITRAN还是CRDS, 都未给出S, 但三者计算的爱因斯坦系数和谱线强度在同一数量级, 且差异不大, 说明, 至少在该波段基于ACPF得到的DMs是准确的。

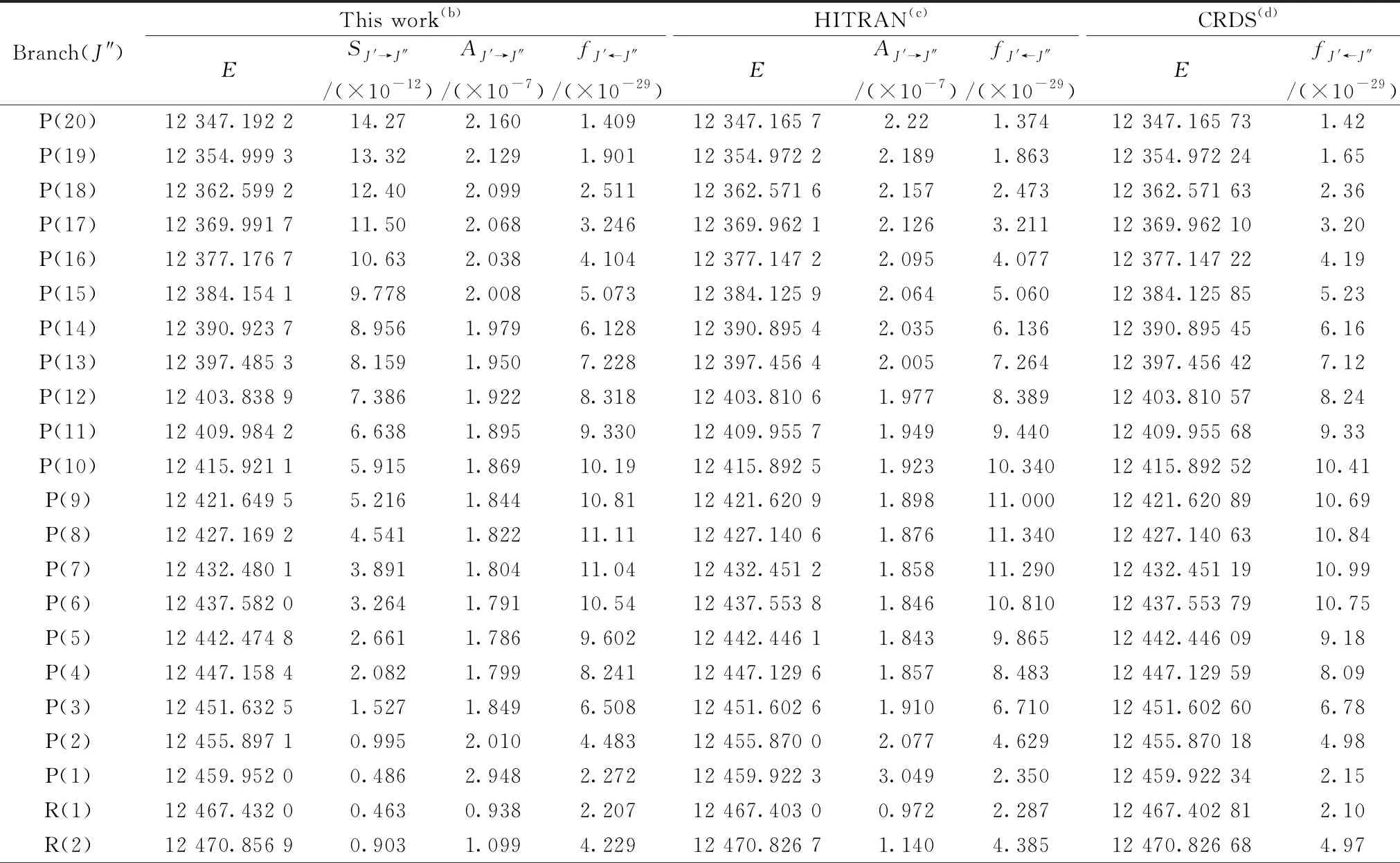
表3 296 K下0-6带的吸收线位置(cm-1)

由式(5)可见, 配分函数Q是关于温度的函数, HITEMP给出了最大温度为3 000 K的配分函数, 将其扩展到9 000 K, 由图6可见, 当前结果与HITEMP给出的Q值符合很好, 在更高的温度段Q值构成的曲线光滑, 连续, 且满足e指数形式。

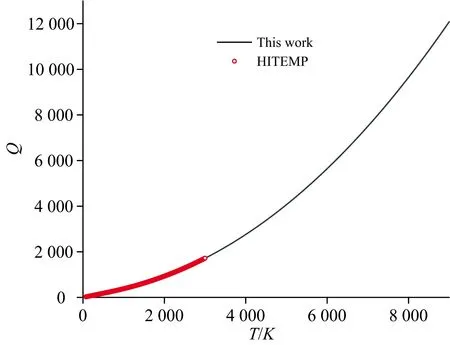
图6 配分函数

基于式(4)可知, 谱线强度随温度变化, 这是测温模型的理论基础之一。 图7给出了20 000 cm-1内, 对数坐标下谱线强度随温度的变化情况, 在低波段随温度升高, 线强减弱, 在高波段则相反。 为了更清晰地观察振转光谱随温度的变化规律, 我们以ν0-1带为例, 给出其在线性坐标下谱线强度随温度的变化情况, 如图8所示。 随温度升高, 谱线有以下变化: (1) 在中心频率附近, 一些原本强度较大的跃迁线, 其强度整体减小, 一些远离中心频率强度较弱的高J值跃迁, 线强却随温度升高而增加, 这是由于分子玻尔兹曼分布随温度不同, 导致不同能级上的占据数发生变化而引起。 我们也注意到; (2)ν0-1带整体的平均强度减弱, 即带积分面积减小; (3) 无论R支还是P支, 最大谱线的绝对强度随温度增加逐渐减小; (4) R支最大强度所对应的谱线位置进行了右移, P支相反进行了左移, 两者均逐渐远离常温下的中心频率; (5) R和P支最强谱线间的宽度增加; (6) 半峰宽逐渐增大, 谱线由“细长”向“矮胖”转换, 基于这些规律, 可以建立不同的测温模型。

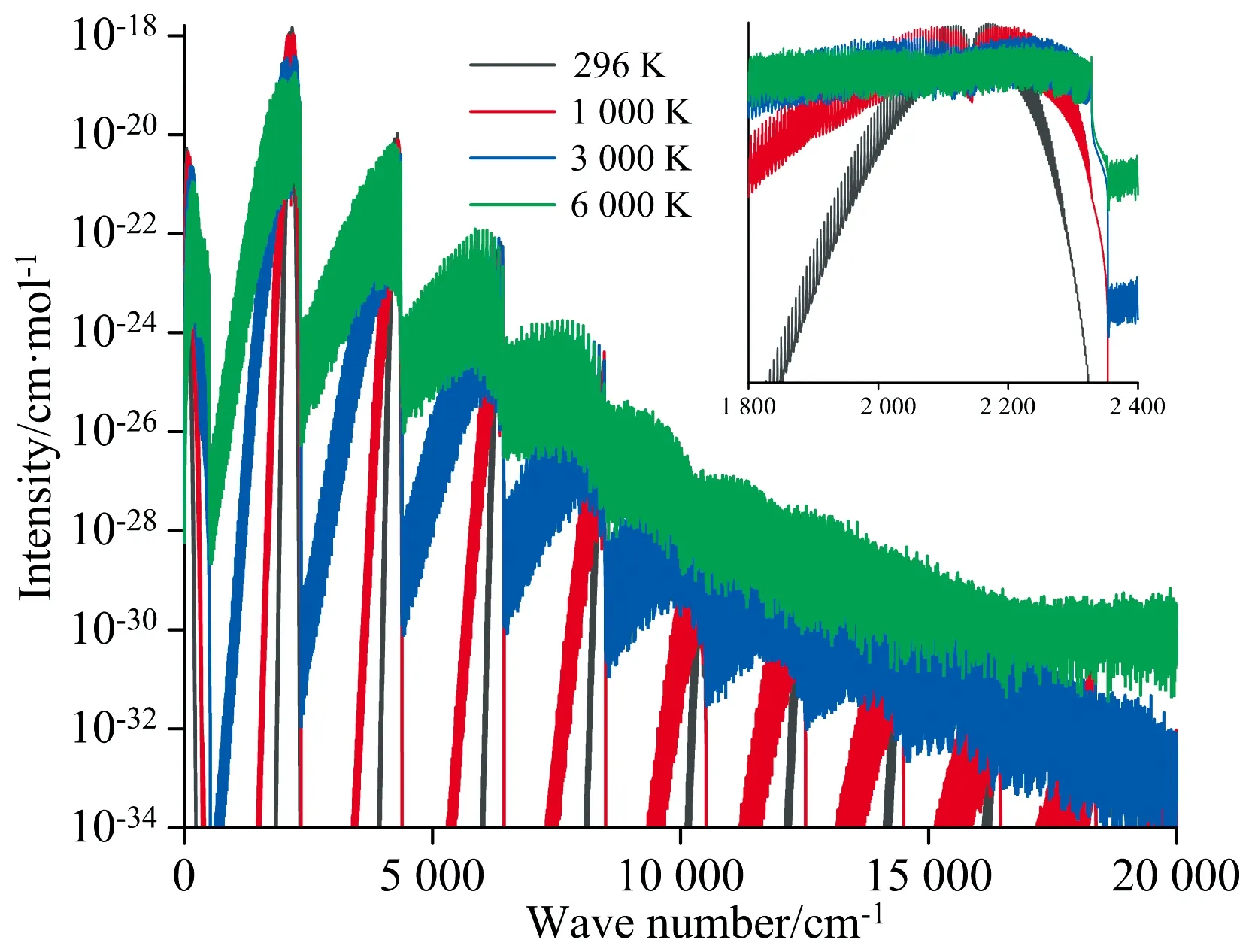
图7 标准大气压下, 不同温度下的振转光谱

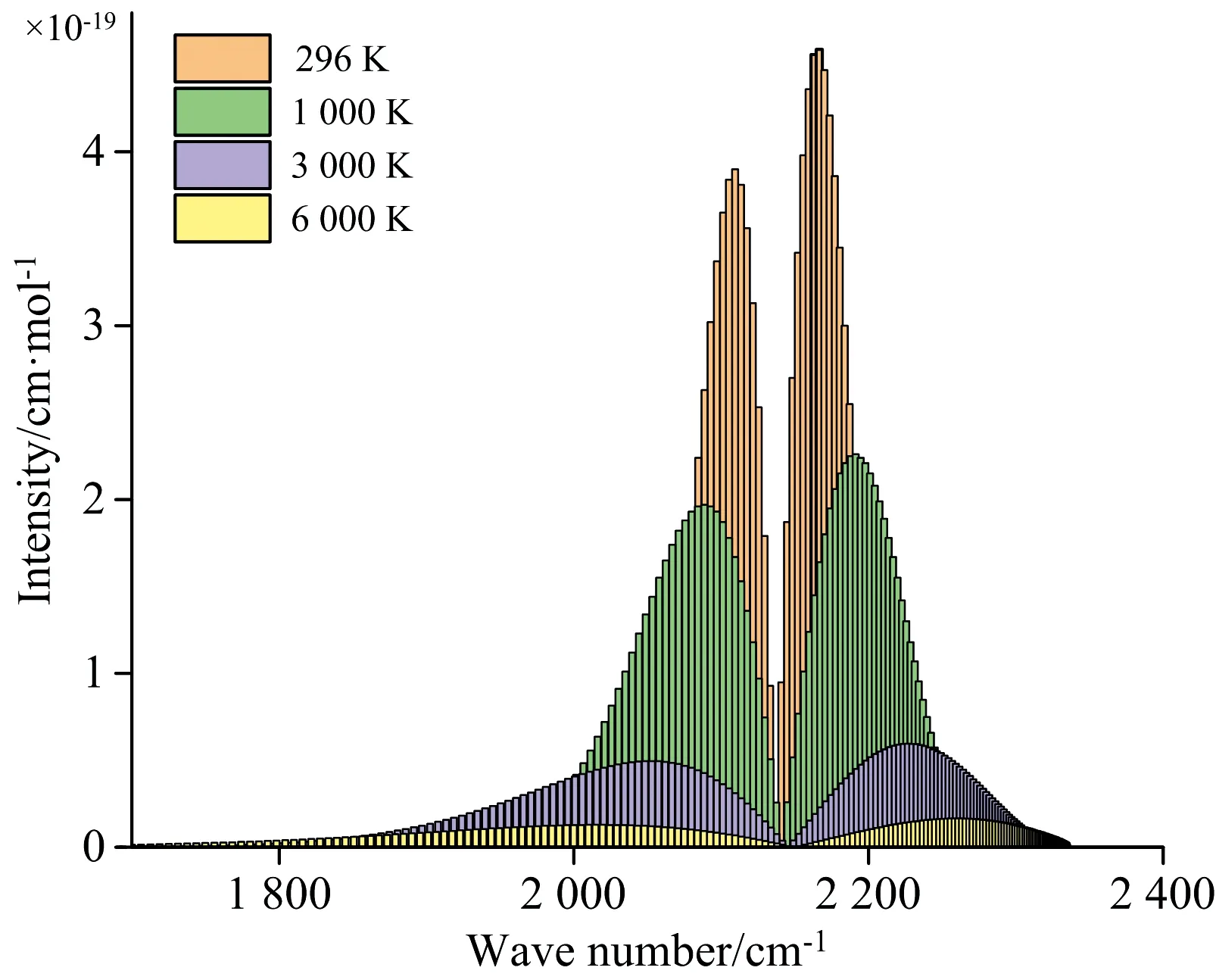
图8 线性坐标下, 不同温度下的ν0-1带振转光谱

理想的振转光谱是线状的, 但分子被激发时, 从一个能级跃迁到另一个能级, 总需要一定的时间来完成, 由测不准原理ΔE·Δt～ћ, 跃迁将发生在一定的能级间隔中, 即谱线具有一定的宽度。 静止分子系统的自然增宽由于很小往往被忽略, 当气体处于高温下时, 以Doppler增宽为主, 在有一定压力时, 气体分子相互碰撞概率增加, 形成Lorentz增宽, 两种增宽效应构成Voigit轮廓。 为了考虑这些效应, 可以对原始线状光谱进行展宽, 作为示例, 图9给出了12C16O在2 115～2 125 cm-1区间内, 0.1 cm-1分辨率下展宽后的光谱图像, 该图可与实验光谱直接比较, 能大大减少从大量繁杂的光谱中找出感兴趣光谱信息的工作量, 为实验选线奠定基础。 由图9, 在中心频率附近, 一些强度较大的跃迁线, 其强度随温度增高反而减小, 一些原本强度较弱的谱线, 线强随温度升高而增加, 部分谱带发生了分裂, 且其中心有了一定的偏移, 均可作为振转谱线测温模型的构建基础。

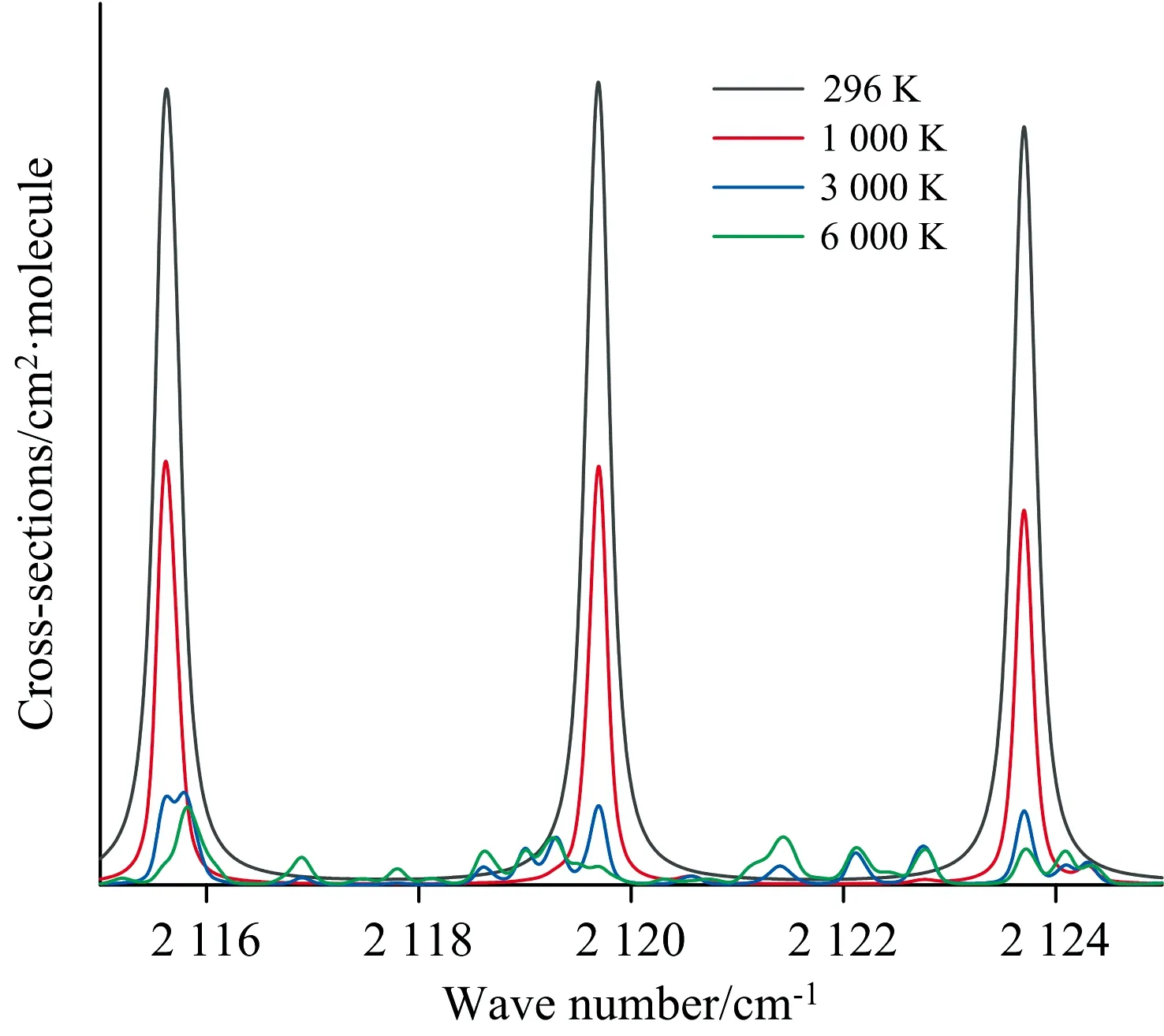
图9 展宽后的振转光谱

图10给出了296 K下, 不同压强时谱线的变化情况, 可以看出, 随着压强增大, 各带的强度整体下降, 谱线轮廓有显著的变化, 该轮廓所包围的面积也相应减小。 与高温下情况不同, R和P带中心谱线位置变化较小, 压力位移不明显。

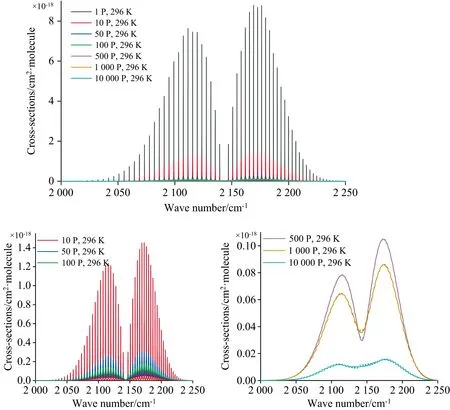
图10 常温下不同压强下的振转光谱

3 结 论

通过RKR方法, 反演获得了12C16O在平衡结构附近的离散势能点, 从十多个常见解析势能函数中, 发现SPF和Morse函数效果最好, 拟合误差均小于0.1 cm-1, Morse在长程上具有光滑性, 但解离能严重偏离实验值。 鉴于此, 将De校正到实验值90 674 cm-1后再次拟合, 进而构建出12C16O基态的一个全新、 全局、 半经验解析势函数。 在此基础上, 将其代入一维薛定谔方程, 全面计算直到解离极限的振动能级、 转动能级和光谱常数, 结果显示, 在平衡核间距附近, 该函数得到的振动能级与实验值符合很好,ν>41的振动能级与文献结果符合较好, 通过对多个MRCI结果分析和对比, 显示了该函数在长程上具有良好的趋势, 说明我们构建的Revised-Morse函数是精确的、 可信的。 之后, 利用从头算averaged coupled-pair functional (ACPF)方法结合能量差分技术获得了ν<63时的偶极矩面、 弗兰克-康登因子、 谱线位置、 爱因斯坦系数, 谱线强度等系列光谱参数被获得, 当前计算值与HITRAN结果符合得非常好。 为了考察振转光谱随温度的变化关系, 进一步计算了温度直到9 000 K的配分函数, 通过考虑展宽效应模拟了不同温度下的“真实”光谱, 多个潜在的测温机理被提出。 最后考察了振转光谱随压强的变化。