基于粒子群算法的锂电池多阶恒流充电方法

何佳琦，张春阳，周 坤

(1.河南科技大学信息工程学院，河南洛阳 471023；2.电力电子装置与系统河南省工程实验室，河南洛阳 471023)

锂离子电池具有能量密度高、循环寿命好、自放电率低等优点，在电动汽车中得到了越来越广泛的应用[1]。目前，锂离子电池充电速度不理想以及对电池寿命预测的不确定性等问题已成为其应用的瓶颈。锂离子电池快速、高效、低损、安全地充电成为电池领域研究的难点和热点[2]。锂电池的一种常见充电策略是恒流恒压充电法，但恒压阶段充电时间太长，不适合进行快速充电[3]。多阶恒流充电是一种改进的充电方法，可以减少充电时间并且控制方法简单，充电过程通常分为五个阶段。

国内外学者对多阶恒流充电进行了优化。文献[4]提出的自适应多阶恒流充电方法，仅考虑对充电时间的优化而忽略了能量损耗，限制了使用条件。文献[5]把充电时间作为目标函数，以锂电池温升和极化电压作为约束条件，使充电时间缩短了20%，但会降低电池的容量保持率。文献[6]提出一种田口粒子群算法来搜索最优四阶恒流充电模式，该方法的目标函数是充电时间和充入电量，但是忽略了充电能耗和电池温升。文献[7]采用启发式优化算法，以充电时间、充电温升和能量损耗为目标函数优化了充电过程，但是该方法计算过程较为复杂。

粒子群算法有很快的收敛速度，并且所需参数较少，计算相对简单，因此用于优化锂电池多阶恒流充电具有实际的研究价值。本文以充入电量、充电时间和充电能量效率为目标函数，提出一种将粒子群算法和五阶恒流充电模型相结合的方法，所得到的五阶充电模式可以在较短时间内提高锂电池的充电容量和充电效率。在实验室搭建了实验平台，完成了五阶恒流充电实验，与传统的恒流恒压充电技术作对比分析，验证了本文所用方法在实际工况中的可行性和优越性。

1 电池模型

1.1 五阶恒流充电工作原理

多阶恒流充电示意图如图1 所示，充电过程符合马斯充电定律。充电初期锂电池的电流接受能力比较强，所以先用一个大电流来快速补足电量，当电池端电压增加到充电截止电压4.2 V 后，充电进入下一阶段，这时使用一个新的较小的充电电流，可以减小电池的极化效应，当电池端电压再次到4.2 V 后进入第三阶段，直到第5 个阶段到达截止电压后视为充电完成。

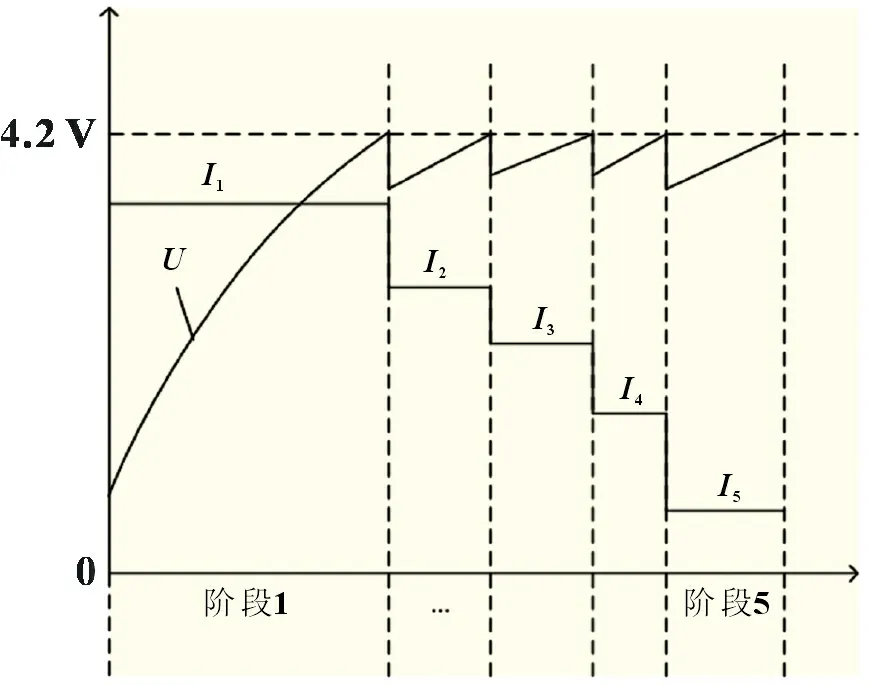
图1 五阶恒流充电原理

1.2 电池模型选择

为了优化五阶段充电模式的充电电流，必须建立一个准确的电池模型。由于二阶RC 网络相比三阶模型较为简单，方便后期的参数辨识和算法计算，相比一阶模型可以更好地描述锂电池的特性，所以本文采用锂电池二阶等效电路[8]，如图2 所示，其中，Uocv为开路电压，Ut为端电压，R0为欧姆电阻，R1、R2为极化电阻，C1和C2为极化电容。

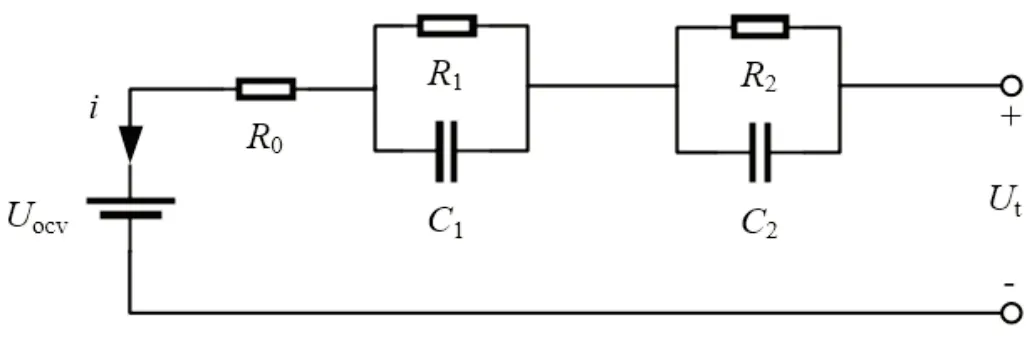
图2 锂电池二阶等效电路

根据基尔霍夫定律可得等效电路公式如下：

式中：t表示时间；i1和i2分别为通过R1和R2的电流；τ1和τ2分别为两个RC 电路的时间常数。

取步长为Δt，仿真中设置为1 s，令i[k]=i[kΔt]，i1[k]=i1[kΔt]，i2[k]=i2[kΔt]，假定充电电流在kΔt至(k+1)Δt这个时间内保持不变，将其离散化，则i1和i2离散化后的表达式为：

式中：SOC0为充电前电池的电荷状态值；C0为电池容量。

同理对式(4)离散化可得：

1.3 电池参数辨识

本文实验以天津力神电池股份有限公司生产的18650 锂电池为研究对象，该锂电池的标称容量为2.5 Ah，额定电压为3.7 V，最大可充入电流为3 A，充电截止电压为4.2 V，放电截止电压为2.75 V。充放电检测设备采用吉林硅能科技有限公司的GN-CD30V15A 电池测试仪，该设备的电流分辨率为1 mA，电压分辨率为1 mV，温度采集分辨率为0.1 ℃，并且可以进行循环控制，所得实验结果通过数据线记录到电脑端。

首先确定电池Uocv的数值，Uocv和SOC存在着相互对应的关系，但是由于电池内阻和极化电压的存在，Uocv不能被直接测量，一般认为同一电流充放电时的极化电压大致相等，但方向相反[9]，所以它们的关系可以表示为：

式中：Uch为充电时的端电压；Udch为放电时的端电压；UR为R0上的电压；UP为极化电压。

由式(6)可得：

具体实验步骤为：电池电量放完之后静置2 h；以0.05C恒定电流给锂电池充电，记录电池端电压Uch和SOC；静置1 h后，以0.05C恒定电流给锂电池放电，记录电池端电压Udch和SOC。用MATLAB 中的拟合工具箱拟合后的充放电电压和开路电压如图3 所示。

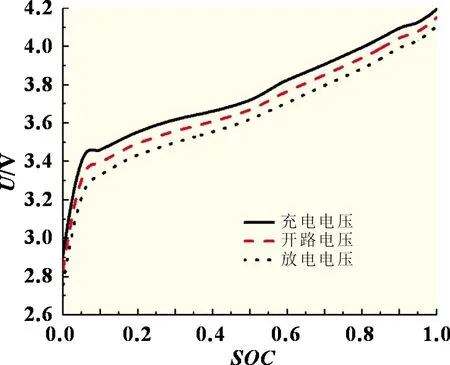
图3 电压和SOC测试曲线

由上述实验获得各个SOC阶段的电压数据，然后根据《FreedomCAR 电池实验手册》进行混合功率脉冲特性(HPPC)实验来实现对电池模型的参数辨识[10]。在MATLAB 拟合工具(cftool)中通过最小二乘法进行参数拟合，得出R1、R2、C1、C2在间隔5%SOC状态下的参数，如表1 所示。

2 充电优化方案

2.1 目标函数制定

充电目标函数是由充入电量(SOC)、充电时间(T)和充电能量效率(η)3 项指标来决定的，公式推导如式(8)所示：

为了方便粒子群算法寻优，将三项指标标准化，设F1为SOC，F2为SOC标准化后的充电时间，则F2可以表示为：

其中，SOCmin和SOCmax分别为90%和100%，Tmin和Tmax分别为2 400 和4 800 s。同样，充电能量效率也由SOC进行标准化，推导如下：

其中，ηmin和ηmax分别为90%和100%。为了在更短的充电时间内获得更大的充电容量和更高的充电能量效率，目标函数和约束条件如下：

式中：α、β和γ分别为充电容量、充电时间和充电能量效率的权重，三个权重值可以根据用户的不同充电需求来设定。本文三个权重都设置为1/3，表示充入电量、充电时间和充电能量效率的重要性是相同的。

2.2 粒子群算法充电优化

粒子群算法通过模拟鸟类捕食的行为，用于优化问题的求解，在动态、多目标优化环境中能有更快速度和更好的搜索能力。充电优化具体步骤如下：

步骤1，生成初始充电模式，根据本文所用的力神18650锂电池的特性，最大充电电流应不大于1.2C(3 A)，因此设置电流范围如下：

设置初始种群有100 个粒子，分别代表不同阶段的电流值，在电流范围内随机取值。

步骤2，建立锂电池五阶恒流充电模型，根据上文求得的不同SOC对应的电池参数建立充电模型，充电流程如图4 所示，N为充电阶数，这里把N的阶数Nstage设置为5，根据本文所用锂电池参数，截止电压U截止设置为4.2 V。

图4 多阶恒流充电流程图

步骤3，计算Pbest和Gbest，对于每种电荷模式，适应度函数可由式(11)计算，将适应度值与其Pbest值进行比较，如果适应度值优于Pbest，则成为新的局部最优值，比较所有粒子中的Pbest，得到全局最优值Gbest。

步骤4，收敛性判定，当全局最优值Gbest不再更新时，就找到了全局最优解，如果没有就进行步骤5。

步骤5，更新粒子位置，由于粒子群算法可能会在搜索过程中陷入局部最优，所以本文通过将变异机制引入粒子群算法中，使算法能够避免陷入局部最优解，找到最优充电模式。当粒子按式(14)更新其位置后，对更新后的位置Ik+1进行变异，若粒子变异后的位置优于Ik+1，则粒子位置更新为变异后的位置，否则不变异。粒子位置按式(15)进行变异，更新粒子后回到步骤2，继续模拟多阶充电求出适应度函数，直到找到全局最优解。式(16)为惯性权重更新公式。

式中：Im(k+1)为变异后的位置；δk为第k次变异时的步长；λ为步长的衰减系数，本文取0.95；2rand()为[0,1]的随机数；k为迭代次数，kmax为最大迭代次数，本文中取100 次；ΔIk为第k次迭代中5 个阶段每个阶段的变化电流；Ik为第k次迭代中所有阶段的充电电流；ωmax和ωmin为最大和最小的权值，分别为1 和0.2；r1、r2为均匀分布的随机值，其变化范围为[0,1]；c1和c2分别为个体学习因子和群体学习因子。

根据种群活动的特点，在算法运行初期，种群所获取的信息比较有限，所以此时的群体经验参考价值较低，在算法早期应当增加c1的取值，但是在算法后期，由各粒子获取了很多最优解信息，此时的群体经验具有较好的参考价值，因此后期c2应取较大的值。在本文中，通过式(17)进行c1和c2的动态取值：

3 结果

3.1 仿真结果与分析

目标函数变化曲线如图5 所示，经过40 次迭代，最佳适应度值不再更新，这意味着得到了粒子群算法的收敛性。结果表明，该优化算法能获得全局最优解，且收敛速度较快。图6 中的SOC曲线、充电时间曲线和充电能量效率曲线也具有很好的收敛特性。为了避免偶然性，进行了多次算法测试，最终得到五阶恒流充电的最佳电流组合为[1.16C,0.78C,0.54C,0.27C,0.1C]。

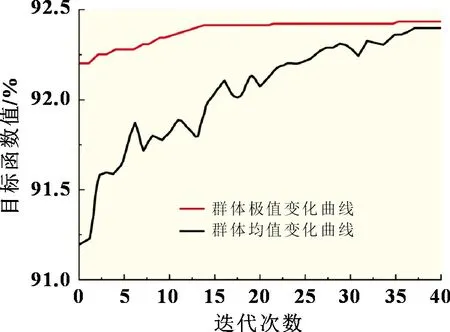
图5 目标函数变化曲线

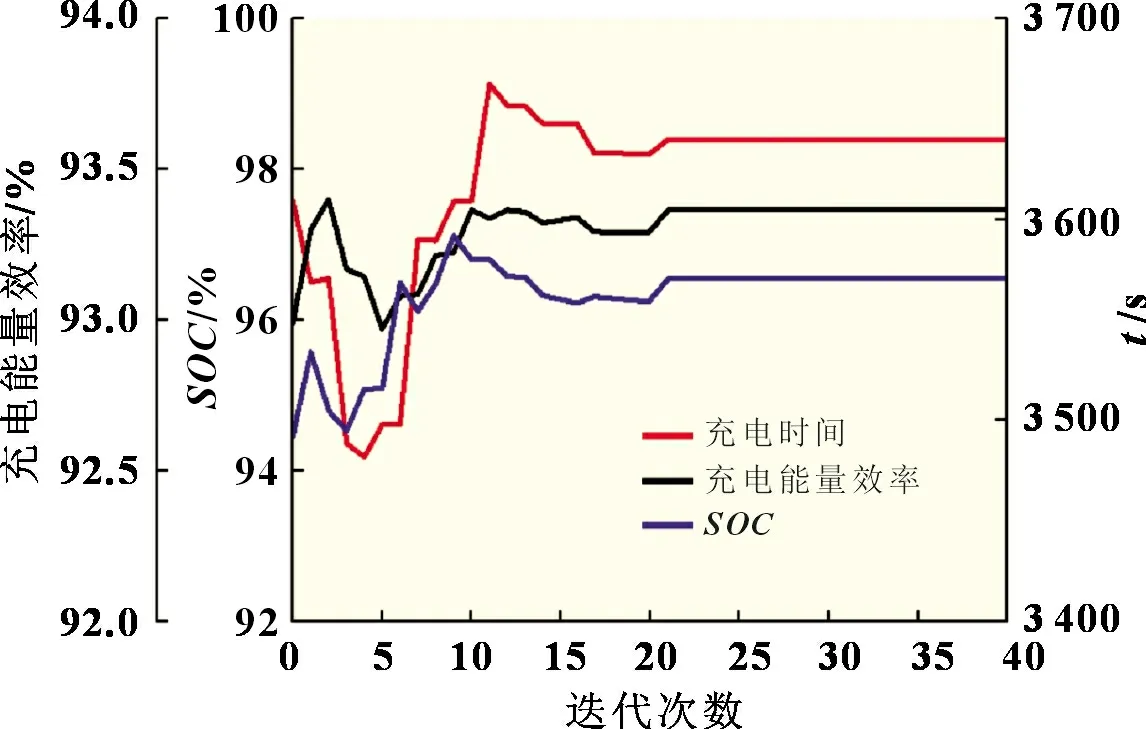
图6 充电时间、SOC和充电能量效率收敛特性曲线

为了验证本文方法的实用性，进行了实验和仿真对比。基于上述算法得到的充电模式，搭建了可以完成五阶恒流充电的Simulink 仿真模型，如图7 所示，主充电电路为Buck 电路，经过滤波后为锂电池输送稳定的直流电，并且设计了放电回路和电流控制方法，充电电源设置为30 V 直流电源，和实验所用电源参数相同，锂电池参数按照前文实验所用电池参数，额定电压设置为3.7 V，额定容量为2.5 Ah，充电截止电压为4.2 V，放电截止电压为2.75 V。实验仍采用吉林硅能科技有限公司的GN-CD30V15A 电池测试仪对前文所述锂电池进行实际工况下的五阶恒流充电实验。仿真和实验的充电结束条件均为第五阶段电池电压达到4.2 V。

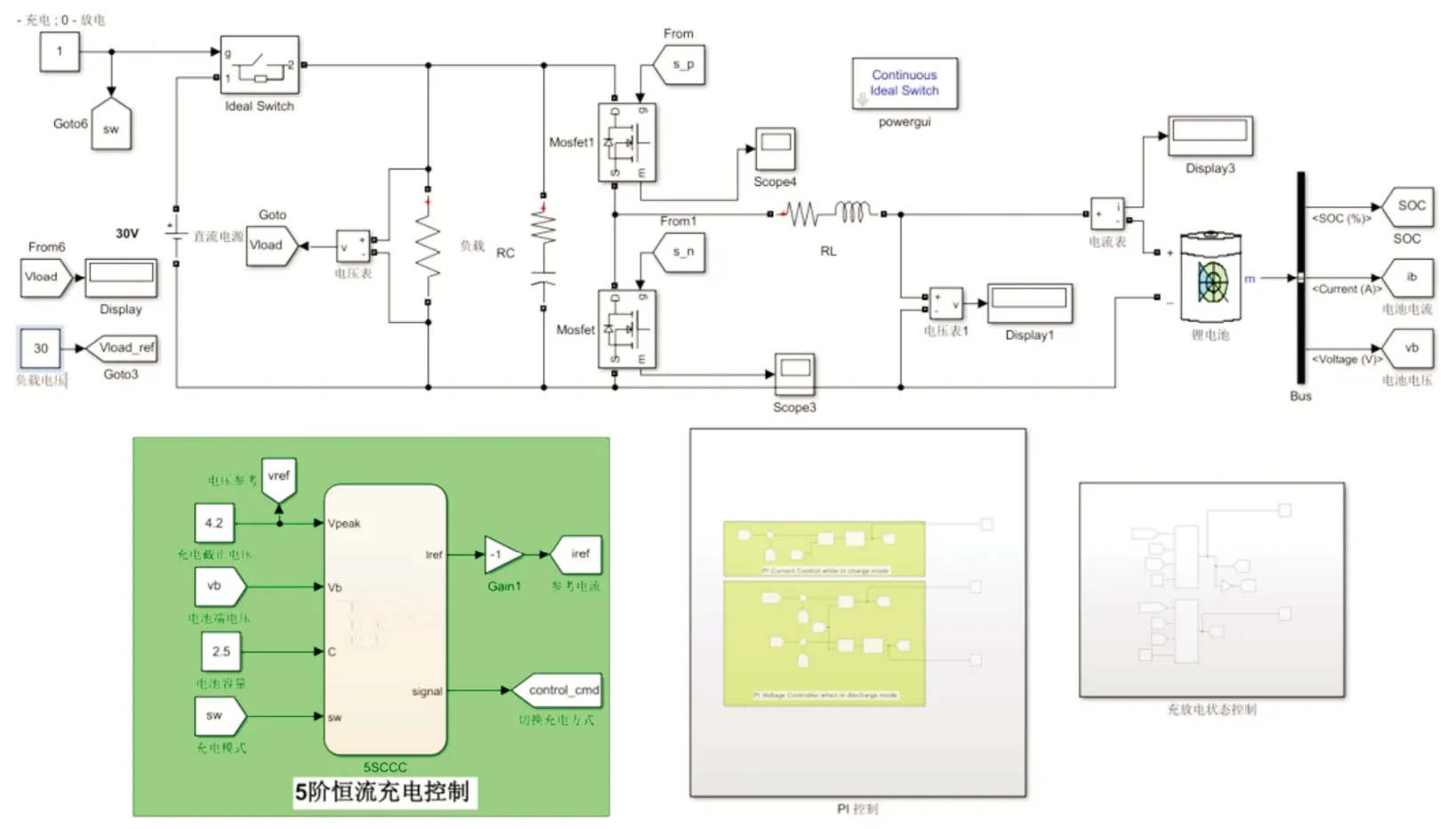
图7 五阶恒流充电仿真模型

图8 为仿真和实验得到的电压、电流和SOC曲线。在图8 中，可以看出实验结果和仿真结果非常接近，实验充电时间为3 634 s，仿真充电时间为3 592 s，两者相差42 s，误差仅为1.15%。实验和仿真SOC分别为96.32%和97.10%，误差仅为0.78%。这表明本文所采用的充电优化方法具有实用性，可以用于实际工况下的锂电池充电。

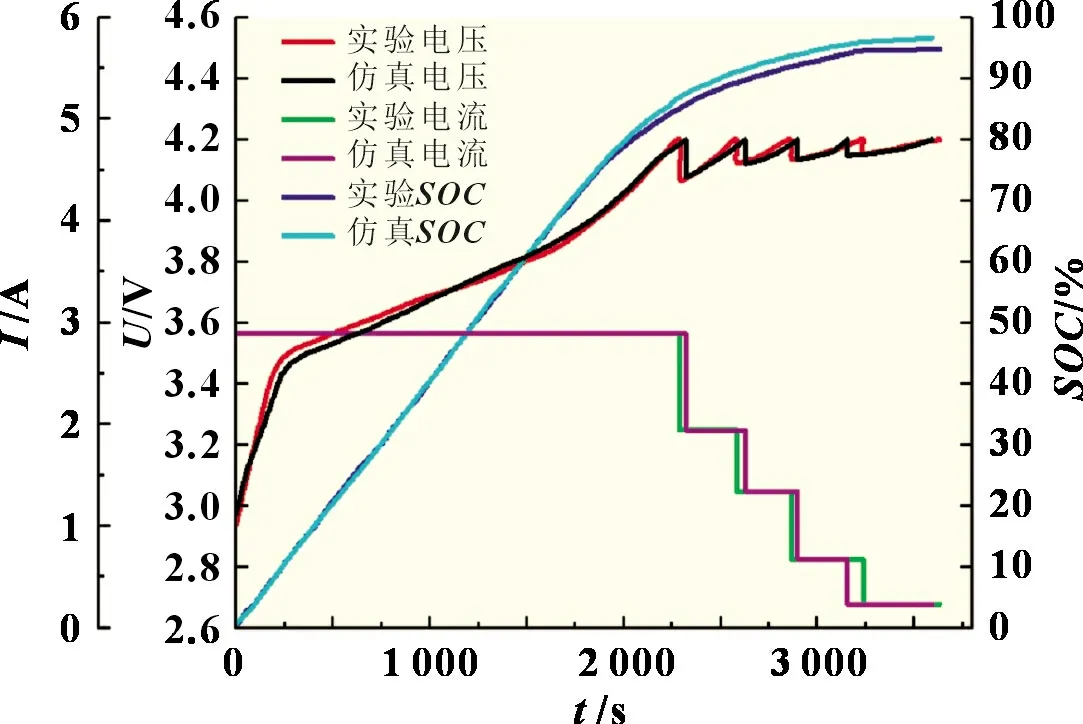
图8 五阶充电的实验结果与仿真结果

3.2 实验结果与分析

采用恒流恒压充电方法与本文所用的五阶充电方法进行了实际工况下的实验对比。实验选取充放电性能良好的力神18650 锂电池，以0.5C电流将电池充入95%SOC，静置1 h 后，同样用0.5C电流放电到截止电压，静置1 h 后，进行充电实验。

恒流恒压充电过程中，恒流阶段电流设置为五阶恒流充电的最大电流1.16C(即2.9 A)，在锂电池端电压达到4.2 V 时进入恒压阶段，在充入电量达到电池容量的95%时结束充电。五阶恒流充电中，使用粒子群寻优算法求得的电流组合[1.16C,0.78C,0.54C,0.27C,0.1C]对锂电池充电，每个阶段的切换条件为端电压升高至4.2 V，同样在充入电量为95%电池容量时结束充电。对比实验中锂电池电压、电流和温升随时间变化曲线如图9 所示，本文所用五阶恒流充电方法在充入同等电量的情况下有助于加快充电速度并降低充电过程中的温升。并且在五阶恒流充电方法中，温升在第一阶段充电结束时达到最大值。

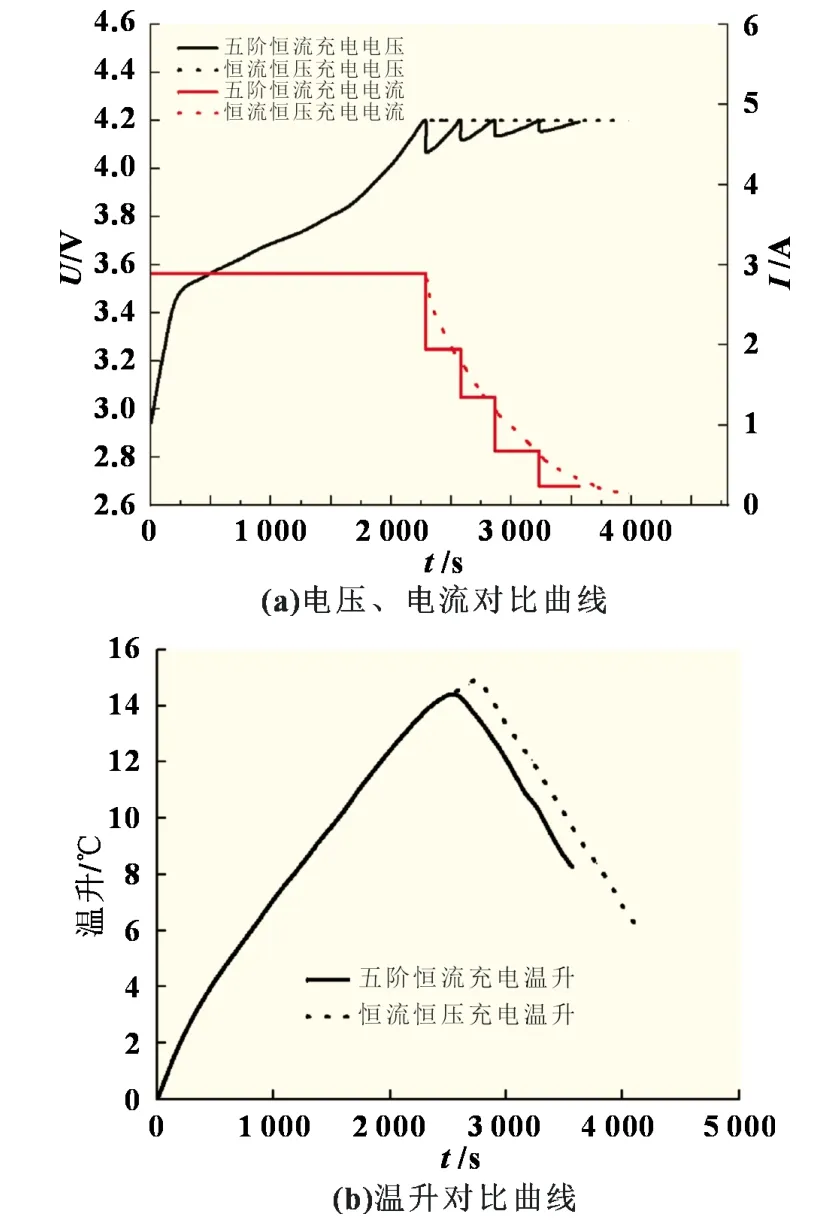
图9 充电过程中电压、电流和温升对比曲线

两种充电方法实验对比结果如表2 所示。由表2 可知，在充入相等电量的情况下，本文所用充电方法的充电时间为3 564 s，比恒流恒压充电法的充电时间缩短了415 s，而且最高温升降低了0.6 ℃，充电能量效率提高了0.37%。

表2 两种充电方法对比

4 结论

本文针对锂电池恒流恒压充电时间过长和充电过程中电池温升大等问题，提出了一种将粒子群算法和多阶恒流充电模型相结合的方法来对锂电池充电方法进行优化，使锂电池可以在给定充入电量的条件下缩短充电时间，降低电池温升。使用Simulink 仿真和实验进行对比，验证了本文所用方法获得的充电模式的实用性。与传统的恒流恒压充电法在实际工况下进行了对比，实验结果表明，与恒流恒压充电方法相比，本文所用优化充电方法在充入相同电量的情况下，可以大大减少充电时间，提高充电效率，并且降低了电池最大温升。这证实了本文所用的优化充电方法能使锂电池充电更加安全快速，对锂电池充电的研究有着重要意义。