基于软木微结构仿生的轻质多孔结构设计与力学仿真分析

李 旺 魏新莉 潘 俊 杨 冰 苏利江 马炜袁

（中南林业科技大学，湖南 长沙 410004）

结构仿生是一种对生物体巧妙的结构进行模仿，并将具有类似生物体结构的形态应用于工业制品与产品设计中的仿生学方法[1-5]。Speck等[6]研究了空芯植物的管壁结构，仿生出一种可变刚度的轻质结构。雷永鹏[7]对网状丝瓜络结构进行剖析，开发出类似泡沫金属的新型轻质多孔结构材料。Julian等[8]摹仿昆虫的表皮角质层结构，研发了高效和轻量的骨架结构。Ma等[9]设计了一种基于蜻蜓翅膀薄壁结构的轻质仿生飞机加固框架。宋文伟[10]基于甲虫鞘翅的空腔微结构，构建了一种力学性能优异的小柱孔结构模型。现有报道为软木微结构的轻质多孔结构仿生研究提供了灵感与启发。

软木又称栓皮，是栓皮栎（Quercus variabilis）或栓皮槠（Quercus suber）的外皮部分，其细胞骨架构型呈多层空间网络状、壁腔比小，具有质轻、保温隔热、消音减震等优点，兼具结构巧妙和性能优异双重特性[11-13]。鉴于此，本文以软木细胞微结构为仿生对象，利用仿生学原理开发了一种家具用轻质多孔仿生结构，并对仿生结构进行抗压与抗弯性能仿真分析，探讨其在适量载荷下仿生结构的变形模式和结构强度，以期为家具领域的材料开发提供更多选择，同时为软木木材开发和林业产业发展奉献一份力[14-15]。

1 结构仿生原理

结构仿生是将生物体优异性能应用于工业制品与产品结构的一种方法，通过对仿生原型进行类比选择和分析，综合得出最优结构[16]。相似性理论是结构仿生的基础，主要分析仿生对象与仿生结果两者间的结构形状、排列方式的相似匹配度[17]。完成结构仿生后，需对仿生结果和仿生原型进行相似度分析，以检验仿生设计是否具有合理性[18]。

相似度分析：利用模糊数学中的相似理论[19]计算软木微结构与仿生结构之间的相似度，设相似度为Q。

式中：i=1，2，…n；j=1，2，…n；uij为因素i对因素j的重要性比较结果，通过判断矩阵可计算特征向量β。

上述判断矩阵中原素uij为人为选择判断，受主观影响较大，需要对矩阵P进行一致性检验，以保证其准确性和可信度，判断矩阵的一致性准则为：

式中：CR为检验系数；CI为一致性检验指标；RI为平均随机一致性指标。

在一致性检验后，计算相似元相似度q(ui)[20]：

式中：k，l为相似要素相似特征数量；n为两相似要素共同的相似特征；dj为特征权数；rij为特征值比例系数。

计算得到相似元相似度q(ui)的值后，将其代入式（1）可得相似度Q值。Q值越趋近于1，说明两者之间的相似程度越高，即仿生设计更合理。

2 软木微结构分析与仿生设计

2.1 软木微结构分析

在软木横切面和径切面上，细胞结构特征相似。从几何学上分析，细胞皆为多边形，单个细胞形状基本为四边形，极少数细胞呈五边形和六边形。而在弦切面上，软木细胞多数情况下呈六边形，相邻的三个软木细胞壁相交于一点，只有少量细胞呈五边形、七边形。根据统计计算，弦切面上五边形、六边形、七边形的软木细胞约占细胞总量的95%[21]。根据软木微结构分析，细胞由封闭的网络状空腔结构构成，属于轻质多孔材料。如图1所示，从软木细胞的局部微观形貌图中（图1a）测得，软木细胞单体的直径D为25～35 μm，底面边长L为12～25 μm，细胞壁厚H为0.7～2.0 μm。通过离析实验提取软木单体细胞，从分离出来的单个细胞微观形貌图中（图1b）可见，软木细胞单体为类棱柱状[22]。参考软木单体细胞尺寸的测量值，对仿生单元的尺寸在测量值的基础上进行放大优化，软木单个细胞被简化定义为内部中空的正六棱柱，如图1c和图1d所示。其中，细胞弦切面（顶、底面）形状为正六边形，横切面与径切面（侧面）形状为矩形。

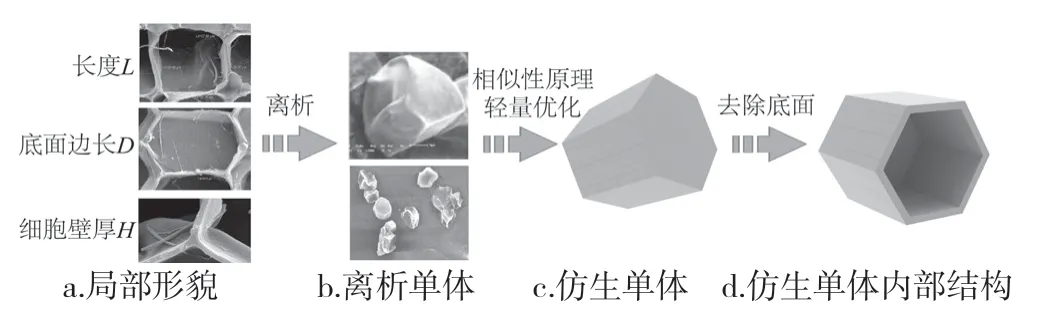
图1 软木细胞仿生单元Fig.1 Cork cell bionic unit evolution process diagram

2.2 软木仿生结构设计

以软木微结构形成的层状细胞骨架为仿生对象，通过Creo三维建模软件[23]进行仿生结构CK的设计与建模。运用结构相似性原理，设计了CK-1 型、CK-2型仿生轻质结构和对照组CK-3 型等体积实心结构，设计过程如图2 所示。 CK-1 型结构模拟软木单体细胞的结构特征，以内部中空的正六棱柱仿生单体为结构单元，并参考软木弦切面的蜂窝状结构与横切、径切面层状结构的分布特点，进行层状结构轻量化仿生[24]。CK-2 型参考树木外表皮的保护机制[25]，在结构上下两端设计了类似的结构保护层，使得CK-2 型结构具有与CK-1 型结构相同的内部结构与层状结构骨架。同时，为了消除无关变量对设计结果的影响，设计了对照组CK-3 型等体积实心结构。

图2 仿生轻质结构CK-1 型、CK-2 型和对照组实心结构CK-3 型Fig.2 Bionic lightweight structure CK-1 type, CK-2 type and control group solid structure CK-3 type

2.3 软木仿生结构与软木微结构的相似度分析

为验证以软木微结构为生物原型进行仿生设计的合理性，进行了软木仿生结构与软木微结构的相似度分析，基于上述式（1）与式（2），建立评价因素集U=｛u1，u2，u3｝={细胞直径，细胞边长，细胞壁厚}，根据比例标度代入判断矩阵中可得P的值：

通过矩阵P可得特征向量β=（0.493 4,0.310 8,0.195 8），对结果进行一致性检验。基于上述式（3）得到，CI=0.026 8，RI=0.52，则CR=0.051 6<0.10，符合一致性检验标准，说明选取的矩阵P是可信的。

通过判断软木仿生轻质结构与软木微结构两个相似系统中各相似元的特征值比值，基于式（4）得到软木仿生轻质结构与软木微结构之间的相似元相似度为：q=（0.82,0.78,0.72），则软木仿生轻质结构与软木微结构之间的相似度Q的值：Q=0.493 4×0.82+0.310 8×0.78+0.195 8×0.72=0.788。

通过上述相似度分析计算可以得出，相似度Q的值较为接近1，软木仿生轻质结构与软木微结构的相似度较好，因此进行仿生设计具有较高的合理性。

3 软木仿生结构力学性能仿真分析

3.1 抗压仿真分析

利用ANSYS Workbench对CK-1、CK-2、CK-3三种仿生结构进行静压缩，选择具有高精确度打印特点的光敏树脂作为三种仿生结构的材质，其弹性模量为E=2 700 MPa，泊松比为0.42，密度为1.15 g/cm3。图3为等效应变图（上）与应力图（下）。由图可知，在压力的作用下，CK-1结构在上层的边缘顶部出现了应变、应力分布不均，最大应变为0.296 7，最大应力为794.61 MPa。CK-2结构的中间部分表现出应变与应力集中，最大应变为0.276 5，最大应力为654.07 MPa。CK-3结构的最大应变与应力出现在模型底部边缘，应变应力分布明显，且最大应变应力小于CK-1和CK-2结构。

图3 三种仿生结构模型等效应变分布图(上)与等效应力分布图（下）Fig.3 Three bionic structure model equivalent strain distribution (upper) and equivalent stress distribution (lower)

根据载荷力-位移的变化计算仿生结构的抗压强度，再由已知仿生结构的相对密度，计算出各仿生结构的比强度值，结果如表1所示。CK-1结构的抗压强度和比强度分别为4.2 MPa和15.3 MPa/(g·cm-3)，CK-2结构的抗压强度和比强度分别为5.3 MPa和18.6 MPa/(g·cm-3)，CK-2结构的抗压强度和比强度值较CK-1结构分别提升12.7%和8.8%，说明CK-2结构较CK-1结构具有更好的抵抗压缩载荷而不失效的能力。CK-3结构的比强度小于CK-2结构，且CK-2结构的材料利用率较CK-3结构提升了72.6%。相较于家具行业常用的蜂窝纸夹芯板[26]抗压强度（0.87 MPa），木质蜂窝复合板[27]抗压强度（2.3 MPa）而言，无论CK-1还是CK-2结构均具有更好的抵抗压缩载荷的能力。

表1 三种仿生结构的抗压强度和比强度Tab.1 Compressive strength and specific strength of three bionic structures

3.2 三点弯曲仿真分析

利用ANSYS Workbench对三种仿生结构进行三点弯曲仿真分析，结果如图4所示。经过仿真计算可得，CK-1和CK-2结构的最大总形变量分别为5.16 mm和5.07 mm，最大应力分别为176.01 MPa和135.49 MPa。在整体形变方面，CK-2结构相较于CK-1结构的各层形变量更小。CK-3结构最大应力则出现在结构底部，最大应力值为102.38 MPa，在三者中最小，因而其横向弯曲适应性最好。

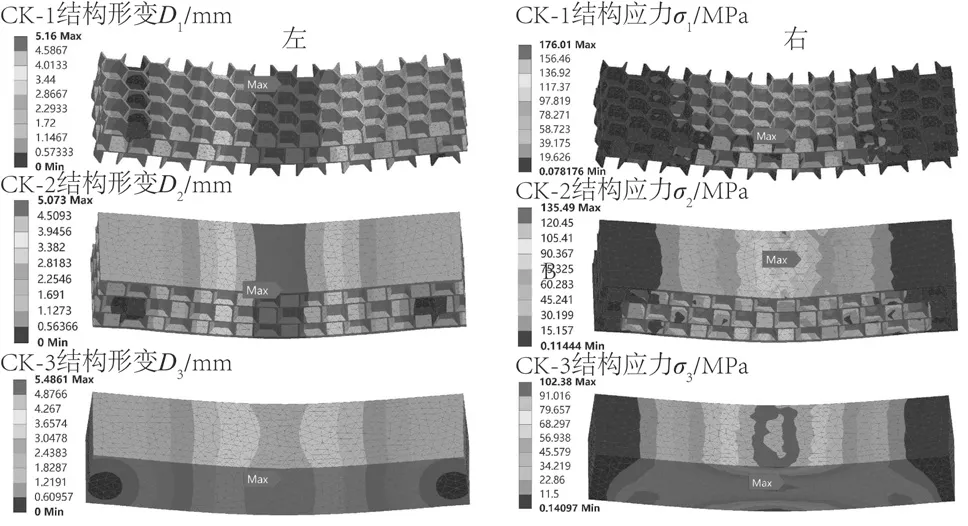
图4 三种仿生结构变形分布图（左）与等效应力分布图（右）Fig.4 Three kinds of bionic structure deformation distribution map (left) and equivalent stress distribution map (right)

根据弯曲力-位移的变化计算仿生结构的抗弯强度，再由已知仿生结构的相对密度，即可计算出各仿生结构的比强度值[28]。由表2可知，CK-1结构的抗弯强度和比强度分别为22.4 MPa和81.45 MPa/(g·cm-3)，CK-2结构的抗弯强度和比强度分别为25.5 MPa和89.47 MPa/(g·cm-3)，比前者分别提升13.8%和9.8%，这说明CK-2结构具有更好的抵抗弯曲载荷。相较于家具行业常用的蜂窝纸夹芯板[26]抗弯强度（9 MPa），木质蜂窝复合板[27]抗弯强度（2.7MPa）而言，无论CK-1还是CK-2结构均有更好的抗弯强度。

表2 三种仿生结构的抗弯强度和比强度Tab.2 Bending strength and specific strength of three bionic structures

4 结论

本文结合结构仿生相似性原理，设计了CK-1和CK-2两种软木仿生轻质结构，并进行了力学仿真分析，主要得出以下结论：

1） CK-2结构抗压强度和比强度均优于CK-1结构，较CK-1结构分别提升12.7%和8.8%，因此CK-2结构能承受更大的压缩载荷，具有更好的稳定性。

2） CK-2结构的抗弯比刚度和比强度均优于CK-1结构，较CK-1结构分别提升13.8%和9.8%，表明CK-2结构能承受更大的弯曲载荷，且不易发生结构突变崩塌的现象，抗弯能力更强。

3） CK-1与CK-2结构的材料利用率均优于对照组CK-3结构，具有更轻的重量，达到了轻量化的设计目的。

4） CK-1和CK-2结构的抗压比强度、抗弯比强度均高于蜂窝纸夹芯板和木质蜂窝复合板，且CK-2结构的力学性能最优。因此，CK-2作为家具用轻质多孔结构具有明显的性能优势。