地铁-电网磁耦合电流在电网回路中分布特性研究*

胡学永 宁晓雁 刘 骁 颜靖东

(1.中车青岛四方机车车辆股份有限公司 青岛 266111；2.西南交通大学电气工程学院 成都 611756)

1 引言

伴随着社会和经济的发展，中国各地区的地铁网络处于大面积铺设当中，地铁引起的电力变压器直流偏磁问题愈发严重，不但影响周边电位分布，腐蚀附近埋地管道等设备，而且会通过接地网侵入电力系统，造成严重的安全事故和巨大的经济损失[1-2]。通常认为由于钢轨非完全绝缘性能而泄漏的杂散电流是导致电力变压器直流偏磁的主要原因。但现场勘测却发现，新修建的地铁线路附近的电力变压器也存在直流偏磁问题，且直流偏磁曲线与地铁运行时刻高度相关，由此可知杂散电流并非导致电力变压器直流偏磁的唯一原因。

依据电磁感应原理，导体中流过交变电流时会在周边产生交变磁场，处于交变磁场环境中的导线回路受其影响，会在导线中产生感应电流。地铁列车规律性的运行方式使得接触网和钢轨中的电流规律性取流，并非时刻保持直流，因而会在空间内激发交变磁场。已有学者对地铁牵引接触网供电系统的电磁场空间分布进行了深入研究。文献[3-4]主要针对DC 750 V 和DC 1 500 V 两种典型供电方式，分析对比空间电磁场的分布特点；文献[5]对比研究了第三轨供电和架空接触网供电这两种供电系统的电磁场空间分布特点。

通常地铁产生的交变磁场会受到混凝土层的影响，但通过实际测量和仿真发现，地铁产生的交变磁场为低频磁场[6-7]，且由于土壤层相对磁导率与空气基本相同[8]，因此，交变磁场能穿越土壤耦合至附近电网回路。由地铁与电网磁耦合产生的感应电流会经由输电线路侵入电力变压器中性点，导致变压器发生直流偏磁问题，且因为输电线路形成的闭合区域面积较大，电网回路中地铁磁耦合产生的感应电流不能忽略。

有学者在针对地铁牵引电流变化产生的交变磁场的研究中提出，该磁场可能会耦合电网回路产生感应电流，即所谓的磁耦合机制，然而此研究仅通过试验监测发现地铁上方的导线回路中存在感应电流，与实际电网回路存在一定差距，并未深入研究磁感应电流特性[9]。因此，为深入探究地铁与电网回路磁耦合机制，探明感应电流对电网回路的影响情况，本文搭建地铁与电网回路耦合仿真模型和电网数值分析模型，计算分析感应电流在电网回路中的分布特点。

2 磁耦合原理

2.1 磁耦合原理分析

地铁列车规律性运行过程中，牵引接触网也规律性地进行取流，因此接触网和钢轨上的电流并非一直保持直流，其牵引电流波形及列车位移如图1所示。依据电磁感应原理，地铁接触网和钢轨上的交变电流会在空间中激发交变感应磁场，由电网输电线路、变压器与大地构成的闭合回路受交变磁场影响，在闭合回路中产生感应电流，感应电流经输电线路侵入变压器中性点，导致变压器直流偏磁问题，最终流入大地。感应电流侵入原理如图2 所示。

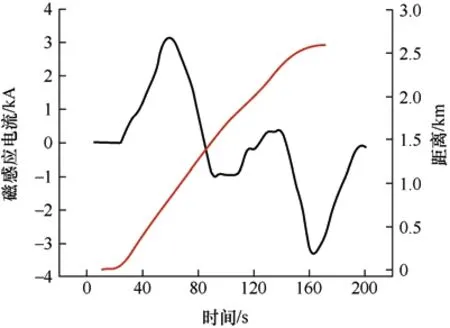
图1 牵引电流波形及位移图

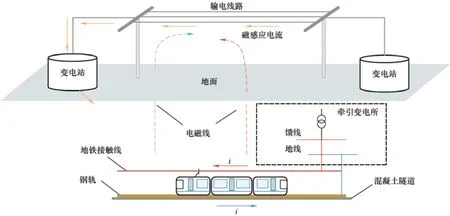
图2 地铁磁耦合感应电流侵入原理

2.2 磁耦合电流的计算

地铁牵引供电回路主要由接触网和回流轨构成，接触网悬挂线直径为毫米级，悬挂线和回流轨的直线长度远大于两变电站之间的距离，且机车运行对磁场分布的影响较小，因此分析时用两条无限长的平行载流导线等效地铁牵引接触网系统。以最简单的电网单回路与地铁线路处于同一平行平面时进行分析(图3)，图3 中L1、L2 分别表示接触网和回流轨，L1 产生垂直纸面向里的磁场，L2 产生垂直纸面向外的磁场；i为忽略杂散电流情况下接触网和回流轨流过的瞬时电流；电网输电线路与大地形成的闭合回路abcd 中，h为回路高度，L为回路并行长度，d1、d2分别为接触线和回流轨与电网回路的最近距离。依据Biot-Savart 定律，距离无限长载流为i的导线在r米处的磁感应强度为

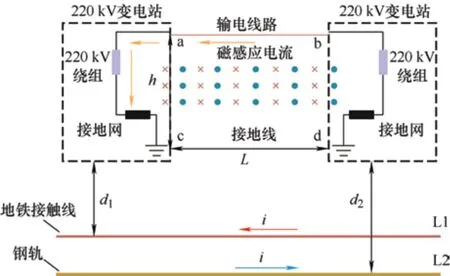
图3 磁耦合电流计算原理

分析式(1)可知，处于无限长载流导线两侧，且与导线距离相等的任意两点处的磁感应强度数值上相等，方向相反，即地铁系统激发的空间磁场对称分布。则电网回路中的总磁通量为

闭合回路中感应电压和感应电流计算公式分别为

式中，n为变压器绕组匝数；R为闭合回路等效总电阻。

观察式(3)和式(4)可知，对某一电网输电回路，感应电压和电流主要取决于磁通量的变化，而影响磁通量的主要因素为地铁线路与电网回路的并行距离(d1)和相对位置、地铁牵引电流。因此本文通过分析磁通量变化趋势，进一步研究分析感应电流在电网输电回路中的特性。

3 模型计算

3.1 磁场分布特性的仿真计算

依据《交流电气装置的接地设计规范》规定[10]，接地网的埋设深度不宜小于0.8 m，但未明确规定具体埋设深度。因此模型中设置接地网埋设深度为极限值0.8 m，等效电网输电线路总高度为40 m；地铁系统部分包括处于相同运行状态的上下行两辆车，线路取一个供电区间长度3 000 m。本文所搭建的模型成立于以下假设。

(1) 地铁牵引供电系统中不存在杂散电流，即接触网和回流轨中流过的电流方向相反，数值相同。

(2) 地铁牵引供电电流取一个周期，即地铁列车完成一次“启动-加速-惰性-制动-停止”。

(3) 周边设备和环境对地铁系统无电磁干扰影响。

(4) 仅考虑地铁系统牵引电流变化引起的空间磁场变化。

地铁与单回路耦合模型如图4 所示。由上至下依次为空气层、近地土壤层、隧道层、土壤层。其中，地铁线路位于隧道层，列车为上下行的运行方式；等效电网单回路跨越空气层和近地土壤层。

图4 地铁与单回路耦合仿真模型

3.2 平行距离对感应电流的影响

为了便于探究电网输电回路并行距离(d1)对电网中感应电流的影响，除了控制大部分变量，如导体属性、回路属性等，并保持地铁牵引回路电流始终为1.8 kA，电网回路处于地铁线路某一侧，且与地铁线路保持平行。此时，电网回路的磁通量、感应电流与并行距离之间的情况如表1 所示。随着地铁线路与电网回路之间距离的增大，磁通量和感应电流都迅速减少，由此推测，在一定距离之外，地铁线路虽然对电网回路仍存在磁耦合影响，但是由于距离较远，磁耦合影响产生的感应电流值极小，基本可忽略。

表1 并行距离与磁通量、感应电流

3.3 相对距离对磁感应电流的影响

工程实际中，地铁线路大多处于地下，电网架空输电线路都处于地上，因而两者在空间中存在重叠、交错等多重情况。本文主要分析两种典型情况：① 电网输电回路全部处于地铁线路的某一侧；② 地铁线路在空间上穿越电网输电回路。为方便进行对比，本文设置地铁线路与电网回路最近距离为定值(4 000 m)，此时电网回路中磁通量情况如图5所示。当地铁线路与电网回路距离相同时，地铁线路在空间上穿越电网回路情况下产生的磁通量更大，由此产生的感应电流幅值上最大可达0.19 A。由此说明，对于穿越电网回路的地铁线路，不论其与电网回路的距离远近，对于电网的磁耦合影响都不可忽略。

图5 不同相对位置的磁通量变化

4 示例分析

4.1 参数设置

某区域内A、B、C 三座变电站与周边地铁线路位置关系如图6a 所示。图6b 为变电站内部接线情况。由于输电线路必须依靠变压器中性点的接地，电流通过变压器的绕组，形成导通电流回路，而一次高压侧与二次低压侧不存在电路上的连接，所以只考虑一次侧的星形连接的电路模型。

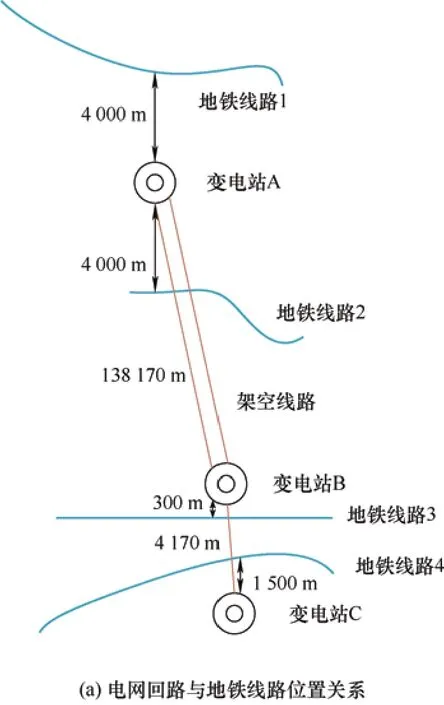
图6 某区域电网回路与地铁运营线路分布

电路按照戴维宁等效模型等效，在变压器正常运行情况下，变压器三相绕组大小相等，对称分布，可等效为直流电阻RT。在双绕组变压器中，单相变压器和三相变压器都可以用以上变压器的直流模型进行等效，变压器的直流电阻可用式(5)表示

式中，RT为单相绕组直流电阻值(Ω)；PK为单相变压器短路损耗(kW)；Un为单相绕组额定电压(kV)；Sn为单相额定容量(MV·A)。输电线路等效直流电阻参考文献[11]，设置为0.03 Ω/km。

4.2 单回路仿真结果

在区域空间内，地铁线路1 未穿越任何电网回路；线路2 穿越AB 回路；线路3 和4 穿越BC 回路。各个地铁线路对电网单回路磁耦合影响下，回路面积内磁通量的仿真结果如图7 所示。图7 中AB回路主要受地铁线路2 和3 的影响，BC 回路主要受地铁线路3 和4 影响；地铁线路1 对两个单回路的影响都不大，基本可以忽略。基于此，计算各单回路内的磁通总量变化及感应电流情况如图8 所示。图8 中AB 和BC 回路的感应电流幅值最大分别为1.94 A、0.71 A。

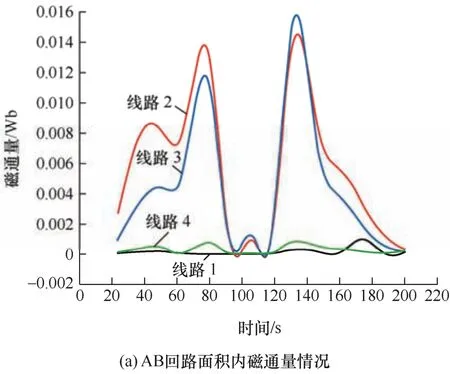
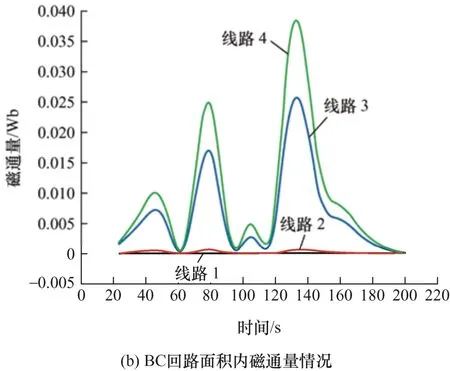
图7 电网单回路磁通量变化情况

图8 单回路磁通总量变化及感应电流

4.3 多回路仿真结果

运用Matlab 搭建双回路电网数值分析模型，模型中分别在AB 和BC 回路添加等效受控电压源。此时变压器中性点电流曲线如图9 所示。

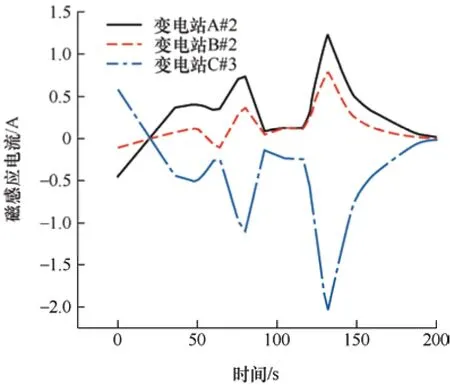
图9 变压器中性点电流波形

图9 中变压器中性点电流最大幅值分别为1.23 A、0.79 A、2.03 A，与单回路模型时的感应电流明显不一致，这表明两回路之间电流在相互传播。

4.4 波形分析

在实际工程中，导致变压器中性点的偏磁电流的因素主要包括雷击、地磁暴感应电流、高压直流输电线路接地极入地电流和地铁电磁耦合电流[12-15]，目前对于前三个因素的研究已经较为成熟，分别有避雷器、地磁暴预测系统、隔直装置对其进行防护[16-20]。而对于地铁电磁耦合电流暂时缺乏有效防护，且当前主流认为杂散电流是导致电力变压器直流偏磁的主要原因，加之在实际测试过程中无法确定周边地铁线路上的各个列车运行位置、运行状态等信息，因而无法直接通过对比仿真和实测结果验证感应电流。

基于此，本文对实测和仿真结果进行频域分析，对比研究电流频率分布，进一步选取数据进行相关性分析，以此论证仿真结果的正确性。同时查阅相关标准，对感应电流的影响程度做出大致评估。

4.4.1 频域分析

图10a 为变电站A#2 号变压器实测波形结果，图10b 为频域分析结果。图10 中感应电流直流分量占比为4.56%，感应电流以0～0.1 Hz 频率分量幅值占比为主。

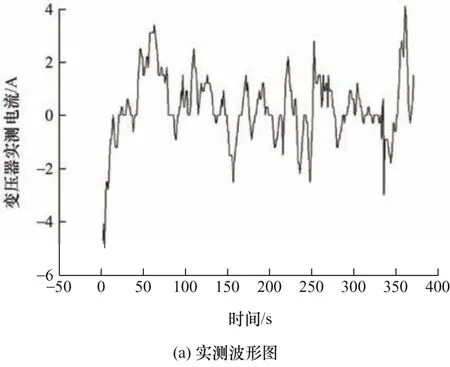
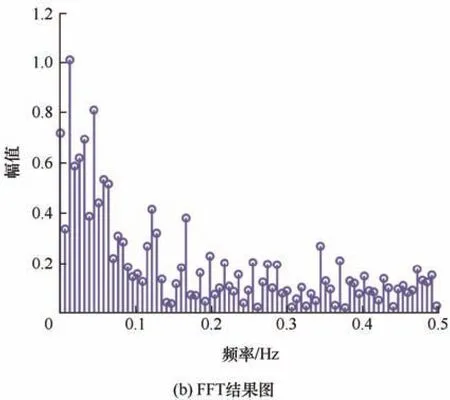
图10 实测结果分析

图11 为变电站A#2 号变压器仿真数据频域分析结果，感应电流以直流分量为主，占比为16.5%，感应电流以0～0.02 Hz 频率分量幅值占比为主。

图11 仿真结果频域分析

4.4.2 相关性分析

综合实测和仿真数据的频域分析结果，选取0～0.02 Hz 内的特征数据进行FFT 结果相关性分析，相关系数C的计算方法如下

式中，COV(x,y)表示x,y向量的协方差，D(x)表示x的方差。根据相关系数划分标准：当相关系数Cxy=1 时，x与y完全相关；当相关系数Cxy=0时，x与y不相关；当相关系数Cxy<0.3 时，微弱相关；当相关系数0.3

表2 相关性分析结果

4.4.3 幅值分析

目前国内外对于变压器直流限值尚无定论，对于额定电流为IN的三相变压器，导则[21]规定直流偏磁时每相绕组的IDC应小于0.7%IN，算例区域内变电站中变压器额定容量均为240 MW，额定电流为630 A，则直流偏磁时每相绕组的IDC<4.41 A。基于该规范，变电站A#2 的感应电流占直流偏磁限值的27.89%；变电站B#2 的占比为17.91%；变电站C#3的占比为46.03%。算例中B 变电站距离地铁线路最近，但磁耦合影响相对A、C 两变电站没那么严重。由此推测，感应电流的流向一般是从靠近地铁的一侧流向远处接地变压器。

5 结论

本文通过搭建地铁与电网回路耦合仿真模型和电网数值分析模型，分析计算了感应电流在电网回路中的分布特点，并通过相关性分析验证了仿真模型与实测结果的数据准确性与相关性，得出了以下结论。

(1) 若地铁线路与电网回路不存在空间上的交错，则随着两者距离的增大，回路磁通量和感应电流不断减少。若地铁线路在空间上穿越电网回路，则不论其与变电站距离远近，回路中感应电流均不可忽略。

(2) 地铁线路对于各个变电站变压器的磁耦合影响依据实际情况不同存在差异。对电网回路而言，靠近地铁线路的变压器受到的磁耦合影响小于远离地铁线路的变压器。地铁磁感应电流存在通过电网回路向远处传播的可能性。