一种接收信号强度的室内定位稳健估计方法

冯阳,杜顺季,叶锦锋

(广州市城市规划勘测设计研究院,广东 广州 510060)

0 引 言

随着工业4.0的推进,越来越多的智能化设备出现在室内场景中,这些室内智能设备的工作都依赖对自身位置的感知,离不开室内定位技术的支持。传统的室外定位技术GNSS、手机基站定位等受建筑物遮挡、室内环境复杂等因素的影响,已经不能满足人们室内定位需求,因此室内定位技术已经成为当前测绘领域的重要研究方向。

目前应用于室内定位的技术主要包括红外、蓝牙、WiFi、ZigBee、射频识别(RFID)和超宽带(UWB)等,其中蓝牙、WiFi、zigBee是基于接收信号强度进行定位[1,2]。红外线室内定位技术的原理是红外线标识发射调制的红外射线[3],通过安装在室内的光学传感器接收进行定位;蓝牙技术则是通过测量信号强度来设置定位的,是一种能量消耗慢,应用与近距离环境下的无线传输技术[4,5];WiFi室内定位技术[6]采用在区域内安置无线基站,根据待定位WiFi设备的信号特征,结合无线基站的拓扑结构,综合确定节点位置;ZigBee室内定位技术[7],通过若干待测节点和参考节点与网关之间形成组网,利用网络相互通信进行位置定位;射频识别(RFID)室内定位技术[8,9]利用电磁感应原理,通过无线激发近距离无线标签,实现信息读取;UWB技术通过发送和接收纳秒级及以下的极窄脉冲传播数据,从而具有GHz量级的带宽,脉冲信号具有穿透能力强、抗多径等优点[10]。

本文介绍了基于测距的常用无线定位方法,详细分析基于接收信号强度(Radio Signal Strength Indicator,RSSI)的测距模型[11,12],提出一种接收信号强度的室内定位稳健估计方法,并通过实验对模型参数进行求解,分别采用最小二乘方法和本文方法进行室内位置解算,并对定位精度进行对比分析。

1 几种基于测距的室内定位方法介绍

目前室内定位的方法有基于测距的无线定位和非测距的无线定位,非测距的无线定位算法主要有:质心算法、凸规划定位算法等。基于测距的无线定位精度相对较高,主要方法有到达时间法(Time Of Arrival,TOA)、到达时间差法(Time Difference Of Arrival,TDOA)、到达角度法(Angle Of Arrival,AOA)以及接收信号强度法等[13]。

1.1 到达时间法

到达时间法(TOA)通过测量信号的传播时间实现测距,利用信号在节点间的传播时间乘以信号传播速度求取节点间的距离。TOA测距分为单向测距和双向测距两种模式,单向测距模式发射器和接收器需保持严格的时间同步,根据信号发射时刻和接收时刻确定信号传播时间,如图1(a)所示。双向测距模式通过在发射器处计算发射器发射和接收器返回信号的时间差,从而计算距离,无须发射器和接收器之间保持时间同步,如图1(b)所示。通过计算信号在参考节点和标签之间的距离,利用三边定位算法求解未知节点的坐标,从而实现室内定位,如图1(c)所示。

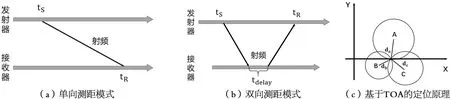
图1 到达时间法定位

1.2 到达时间差法

到达时间差法(TDOA)与到达时间法(TOA)相比,降低了对时间同步的要求。TDOA是通过检测未知节点信号到达两个参考节点的时间差,根据几何原理,未知节点在以两个参考节点为焦点、所测得的距离差为长轴的双曲线上,由三对及以上双曲线相交求取交点即未知节点的位置,基于到达时间差法定位原理如图2所示。

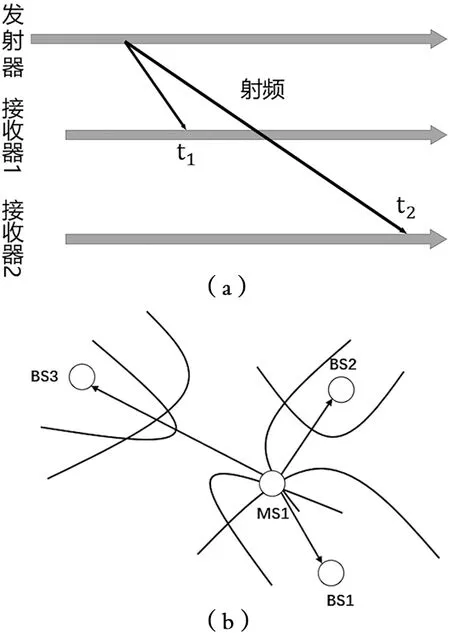
图2 到达时间差法定位

1.3 到达角度法

到达角度法(AOA)定位利用测量信号到达角度的原理,通过参考节点处的天线阵列测量未知节点发射信号的角度信息,由三角测量方法获得未知节点的位置估计。基于到达角度法定位原理如图3所示。

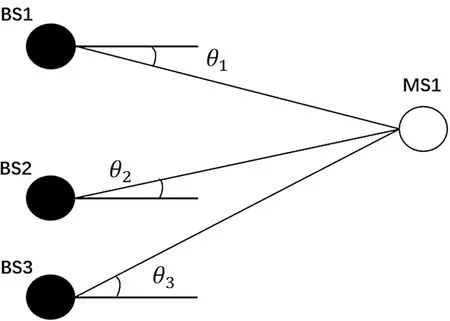
图3 到达角度法定位

1.4 接收信号强度法

基于RSSI的测距是利用无线信号在传播过程中的衰减,根据接收信号强度RSSI值来确定发射器和接收器之间的距离。与上述几种方法不同,RSSI法测距不需要复杂的时间同步和相应的数据交换,不需要额外的硬件辅助设备,是一种简单易行的无线测距方法。接收信号强度法定位如图4所示。

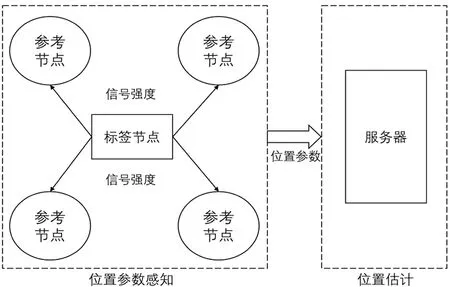
图4 接收信号强度法定位

2 接收信号强度测距的室内定位稳健估计方法

2.1 接收信号强度法测距模型

接收信号强度测距模型分为经验模型和确定性模型,确定性模型有基于求解麦克斯韦方程的时域有限差分法、基于几何光学射线追踪法等,经验模型有线性测距模型、多项式测距模型等。本文采用对数路径损耗测距模型[14],该模型简单实用,是最常用的基于接收信号强度的无线室内测距模型,是一个以理论为支持的经验模型。

在理想环境中,距离d处的接收功率Pr(d)服从Friis传播公式:

(1)

式(1)中Pt为发射功率,Gt和Gr分别为发射器和接收器的天线增益,λ为发射信号波长。

假设各节点的天线增益相同,并考虑衰落效应的影响,根据式(1)可得基于接收信号强度的室内测距模型为:

(2)

式(2)中Pr(d)为距离发射器d处的接收信号强度,单位为dbm,P0(d0)为距参考距离d0处的接收信号强度,n表示信号路径损耗指数,Xσ为衰落效应引起的均值为0,方差为σ2的服从高斯正态分布的随机变量。

取d0=1 m,并设P0(d0)=A且路径损耗指数n已知时,可得Pr(d)的条件概率密度为:

(3)

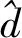
(4)

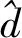
2.2 接收信号强度测距模型误差方程

由2.4节中接收信号强度法的测距模型可得,接收信号强度可以转化为距离,通过测定未知节点接收多个参考节点的接收信号强度,可反算未知节点到多个参考节点的距离。本文采用距离后方交会的稳健估计方法求解未知节点的坐标进行室内定位,稳健估计的原则是要充分利用有效数据,限制利用可用数据和排除有害数据[15]。其观测方程可表示为式(5):

(5)

其中,di为由接收信号强度反算的距离,(xr,yr,zr)为未知节点坐标,(Xi,Yi,Zi)为参考节点坐标。

将式(5)按照泰勒级数展开线性化,可得线性观测方程为式(6):

di=d0+aidxr+bidyr+cidzr

(6)

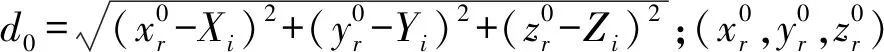
由式(6)可得误差方程为式(7):

(7)

2.3 室内定位稳健估计方法

(8)

在不等权独立观测情况下的稳健估计准则为:

(9)

(10)

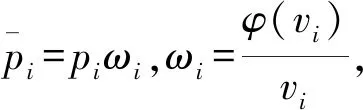
(11)

或

(12)

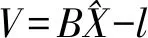
(13)

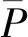
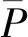
(14)

2.4 稳健估计选权迭代过程

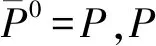
(15)

(16)

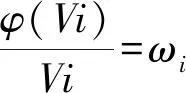
(17)

(18)

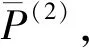
(5)最终的解算结果为

(19)

(20)

在平差计算中,权函数总是随改正数变化而发生变化,且ωi与vi大小成反比,vi越大,ωi,pi就越小,经过多次迭代,含有粗差的观测值的权就会不断降低,从而削弱其在平差过程中的作用,通过平差过程中不断改变权阵最终实现参数稳健估计。

3 实验分析

3.1 模型参数求解

由式(4)可得,基于对数路径损耗接收信号强度测距模型,未知参数为 1 m处的接收信号强度值A和路径损耗指数n,本文实验环境选择在会议室,以发射器为圆心,分别以 1 m、2 m、3 m、4 m、5 m为半径,分别在0°、60°、120°、180°、240°、300°方向依次测量RSSI值30次。A值的获取方式有两种,一种以 1 m处各角度测量RSSI平均值作为A值,实验结果如图5所示,不同方向实际测定的A值均值为-45.1。另外一种将A值和路径损耗指数n当作未知参数,分别在1～5 m半径处,取各方向RSSI平均值作为发射器在1～5 m处的RSSI值,通过对数曲线拟合求取A值和路径损耗指数n。实验结果如图6所示。由实验结果可得,对数曲线拟合求取的A值与直接测量求取的A值基本保持一致,也间接证明了通过曲线拟合法求取模型参数的正确性。

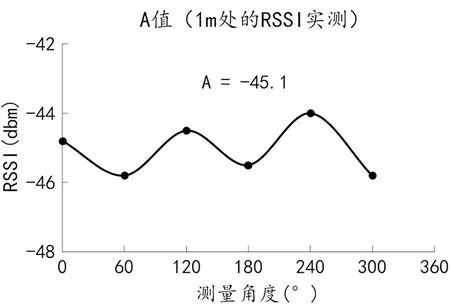
图5 A值实测

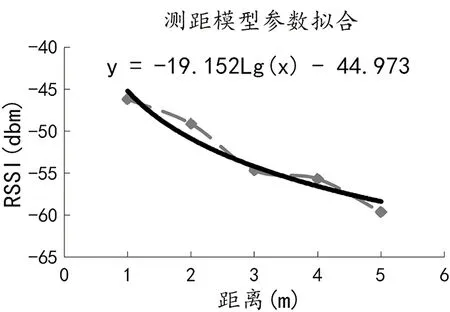
图6 测距模型参数拟合

3.2 定位精度统计

本文选取会议室为实验环境,测试环境具体参数为长 8.8 m,宽 8.0 m,高 3.0 m,自由坐标系定义以会议室西北角为坐标原点,南方向为x轴方向,东反向为y轴方向,向上为Z轴方向。分别在会议室四角及会议室中心布设9个参考节点,参考节点坐标分别为(0,0,0),(8,0,0),(0,8.8,0),(8,8.8,0),(0,0,3),(8,0,3),(0,8.8,3),(8,8.8,3),(4,4.4,1.5)。

在测试环境中随机选取30个未知节点,按照所定义的自由坐标系,事先测定选取的随机未知节点的坐标,通过测定未知节点到参考节点的信号强度反算未知节点到各参考节点的距离,最后分别采用经典最小二乘算法和本文的稳健估计方法解算未知节点定位坐标。

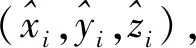
(21)

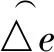
(22)

本文分别采用经典最小二乘和稳健估计方法进行定位解算,两种方法所求得的点位真误差结果如表1和图7所示,实验结果表明同等观测条件下,文本提出的稳健估计定位解算方法结果优于经典最小二乘法。

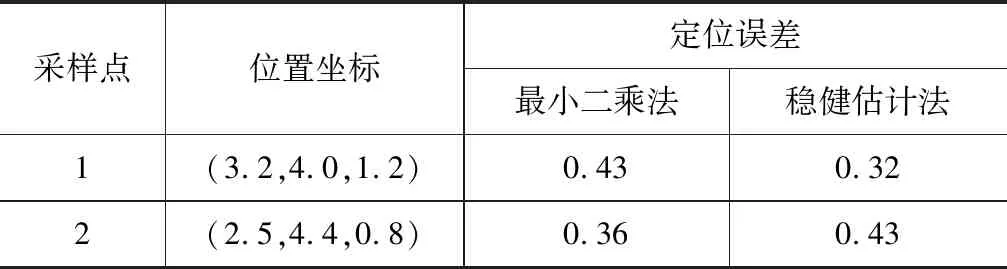
表1 不同方法定位粗差统计

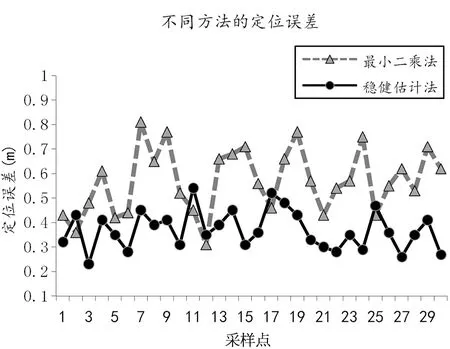
图7 不同解算方法定位误差

4 结 语

本文以接收信号强度(RSSI)的对数路径损耗测距模型为切入点,提出一种室内无线定位稳健估计方法。通过实验求解测距模型参数,并在此基础上,采用距离后方交会实现室内定位解算,最后对比经典最小二乘法和本文方法的定位精度,实验结果表明本文方法定位精度更高,鲁棒性更好。