爆破影响下巷道振速及位移变化规律分析

何 峰,杨 松,王富强,李 彬

(1.辽宁工程技术大学力学与工程学院,辽宁 阜新 123000;2.神华神东煤炭集团,内蒙古 鄂尔多斯 017209)

爆破技术作为一种常规工程手段被广泛应用于矿山的开采以及隧道开挖等各个领域[1-2]。巷道围岩在爆破地震波的作用下会受到不同程度的影响,当巷道围岩质点的振动速度大于巷道围岩最大允许安全振动速度时,巷道将被破坏,尤其是当新建巷道靠近既有巷道时,振动对既有巷道的影响更为突出[3-4]。由此可见,研究地下矿山回采爆破振动效应对地下采场巷道围岩的影响,得出能有效降低爆破振动危害的控制措施是亟需解决的问题。

为了解爆破振动对巷道的影响,国内外学者进行了一系列的研究。Siskind D E等[5]讨论了无限大、均匀、弹性介质中的球形空腔受爆炸时的压力问题;吴波等[6]结合强度折减动力分析法和数值模拟,对隧道中隔岩进行动力安全系数分析;Spathis A T[7]运用FLAC3D软件模拟了炮孔压力函数,并运用该函数得到了围岩振速的计算公式;Coursen D L[8]提出了一种减少延迟爆破地面振动的拟议方法;赵晓等[9]通过FLAC3D对爆破振动作用下巷道的稳定性进行了分析,发现距爆心越远,质点峰值振速衰减得越明显;徐振洋等[10]结合岩石的性质以及装药量与爆心距对公路爆破测振的信号进行了HHT分析,得到了爆破振动的主要能量频带大致分布在10～60 Hz;皇民等[11]采用FLAC3D软件对不同方向的爆破地振波作用对巷道稳定性的影响程度进行分析,发现爆破地振波对巷道水平方向的影响最为明显;张继春[12]通过对三峡工程的基岩进行爆破试验,发现在试验中所得到的基岩质点的振动速度要比采用萨道夫斯基的经验公式估算的值要小,并且在爆破近区的误差更加明显;乔宪队等[13]通过FLAC3D运用耦合柱状的装药形式爆破,对邻近隧洞的影响进行了数值模拟研究;王振毅等[14]运用了ANSYS/LS-DYNA软件,建立有限元模型来模拟研究硐室的应力场以及位移场和速度场的特征;夏昌敬等[15]运用ANSYS/LS-DYNA软件对爆炸产生的冲击波在岩体巷道中的传播和能量的损耗进行了数值模拟,发现在爆炸近区,爆炸应力波衰减会较快。

以上研究表明,爆破振动对巷道稳定性影响明显,但前人研究对象都比较广泛,没有细致地对爆破振动影响下巷道质点的振速和位移变化规律进行分析。基于上述问题,以某露天矿爆破开采对相邻煤矿巷道的影响为研究背景进行数值模拟研究,并且对现场监测结果进行位移收敛分析,对爆破振动影响下矩形巷道质点的振速和位移变化规律进行更深入的研究,为保证巷道稳定、矿山安全高效生产有着重要意义。

1 工程概况

内蒙古某露天煤矿基本形态为单斜构造,煤层倾角为1°～3°,开采深度为50～240 m,属非深部矿井,顶板相对稳定,岩性为较软岩。井田分为4个盘区,主要开采1-2、2-2、3-1煤层。目前回采的1-2煤三盘区,集中回风巷、主运巷及三盘区辅运大巷,布置于井田南界。由于相邻煤矿巷道自西向东主要受到露天煤矿504区、404区下、405区下、305区和406区爆破振动影响,影响长度达1 400 m左右,加之巷道支护设计之初没有考虑动荷载影响,已对相邻煤矿三盘区安全高效回采造成威胁。在此露天煤矿爆破开采过程中,通过合理的爆破设计、测试分析、数值模拟,采取切实可行的爆破减振措施,在保证矿山正常生产和安全生产的前提下,有效降低爆破振动的动力效应和损伤效应,确保巷道安全的爆破最小安全距离,减小爆破振动对邻近边坡的危害,避免边坡的破坏、失稳滑移,开展露天煤矿开采过程研究以及开展爆破振动效应对邻近煤矿辅运平硐的影响,具有十分重要的理论意义和经济价值。

2 数值模型建立

论文运用Auto CAD以及南方Cass软件绘制出巷道与采区位置及爆破点的剖面图,如图1所示。

图1 地质平面Fig.1 Geological plan

由图1可知,模型左侧高143 m,右侧高39 m,左侧巷道高4 m,宽6 m,中间巷道宽度较左右侧的小,宽度为5 m,右侧巷道宽6 m,高4 m。炸药埋在2 m以下的深度,长度为5 m,封堵为2 m。第一个巷道顶面与爆破点的水平距离为68 m,竖直方向与离爆破点的距离为18 m;第二个巷道右侧顶点与爆破点的水平距离为98 m,因为巷道都在同一直线上,所以竖直方向与爆破点距离与右侧巷道相同,均为18 m;最左侧巷道右侧顶点与爆破点的水平距离为128 m,竖直方向距离为18 m。

将图1导入到ANSYS/LS-DYNA中,通过ANSYS软件构建有限元模型,并进行网格划分,划分出巷道、炮孔区域以及炮孔区域填塞和岩石材料的位置,如图2所示。模型各个边界设置为无反射边界,隧道已开挖区设为自由边界。

图2 网格划分后的模型Fig.2 Model after meshing

定义二次黏度系数为1.5,线性黏性系数为0.06,建议刚度系数不超过0.14,沙漏系数为0.1,时间步长控制为0.9,计算时间为0.05 s,定义好各项参数后,输出文件类型为LSDYNA,输出k文件。由于ANSYS/LS-DYNA中没有空气及混凝土和炸药的材料模型,采用线弹性模型,利用软件Textpart对炸药、混凝土以及空气的材料参数进行修改,修改完成后,运用ANSYS/LS-DYNA软件进行求解,将计算结果导入LS-PrePost后处理程序进行数据处理。得到的炸药和空气域以及封堵的模型,如图3所示。

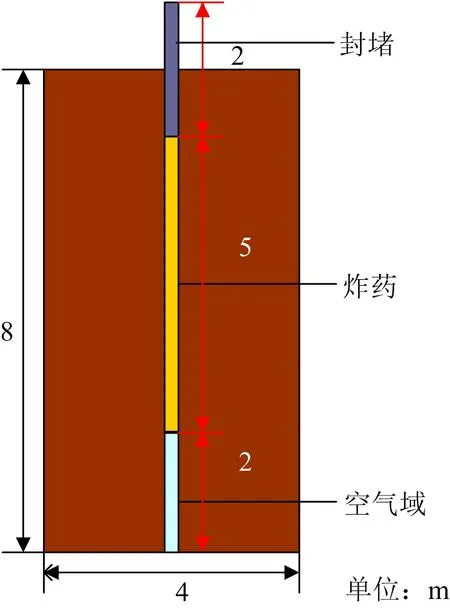
图3 炸药和空气域以及封堵的模型Fig.3 Explosives and air domains and blocking model

由图3可知,炸药选取质量为150 kg的乳化炸药,埋在2 m深的地下,高度可达5 m,周围被空气域包裹,空气域宽度为4 m,高度为8 m,封堵高度为2 m,基本符合剖面建模图形。

3 模拟结果

爆破振动所产生的地振波会对岩层及巷道周围造成极大的破坏力,在爆破振动的影响下,爆破地振波由爆源处向周围扩散,使巷道周围各质点都会产生相应的位移和速度,当爆破引起巷道围岩内质点的振动速度大于巷道围岩允许的最大安全振速时,巷道会被破坏。所以在爆破振动影响下,巷道周围各质点振速大小的变化情况也是衡量巷道变形的标准。

3.1 巷道周围质点的速度分析

将计算结果代入LS-PrePost进行后处理,导出位移速度云图后,在巷道周围取质点,导出各质点的位移和速度随时间的变化曲线,对其变化规律进行分析,各质点编号及位置如图4所示,爆破前、中、后期速度矢量云图如图5、6、7所示。

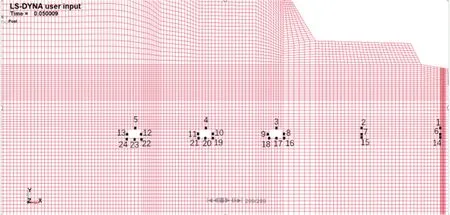
图4 取点的位置Fig.4 Location of the point

图5 速度矢量云图-爆破前期Fig.5 Velocity vector cloud map-early stage of blasting

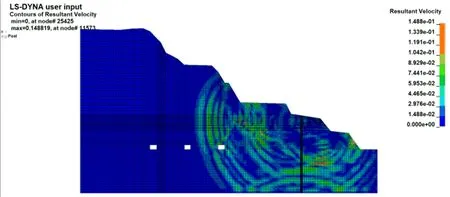
图6 速度矢量云图-爆破中期Fig.6 Velocity vector cloud picture-medium blasting period

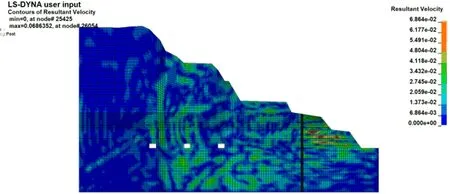
图7 速度矢量云图-爆破后期Fig.7 Velocity vector cloud map-late blasting

通过观察爆破前中后3个时期的云图,可以得到各个质点速度的大致分布情况。在LS-PrePost后处理模块中,分别选中模型中的1～24号质点进行计算,导出各个质点的最大振速值,如图8所示。

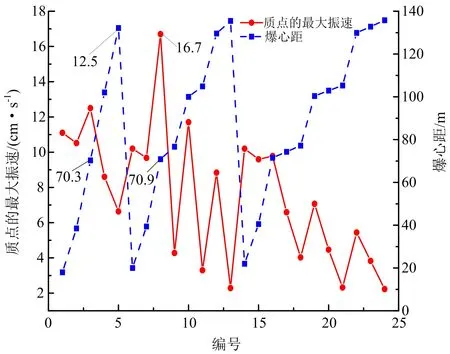
图8 巷道上各质点的最大振速和爆心距Fig.8 The maximum vibration velocity and blasting center distance of each particle on the roadway

巷道拱顶决定了整个巷道的稳定,巷道拱顶质点为3～5号质点,其中5号质点爆心距最大,所以对5号质点进行分析。在爆破开始至0.029 8 s时,其速度达到最大值6.64 cm/s。位于同一水平面上的1～5号质点,与爆破点的竖直方向距离相同均为18 m,水平方向距离由1～5号质点依次增加。1～5号质点的最大速度分别为v1=11.1 cm/s,v2=10.52 cm/s,v3=12.5 cm/s,v4=8.6 cm/s,v5=6.64 cm/s。所呈现的规律是v1>v2,v3>v4>v5,其中3号质点、4号质点和5号质点位与3个巷道拱顶,爆心距依次递增,振速依次递减。

在最右侧巷道,8号质点的爆心距小于3号质点,而8号质点的振速明显大于3号质点的振速,这是由于8号质点位于巷道右侧边墙中部,为迎爆侧,3号质点位于此巷道拱顶中部,迎爆侧振速比拱顶要大,说明两点的约束条件对振速有一定的影响。在同一巷道迎爆侧,8号质点振速大于16号质点,10号质点振速大于19号质点,12号质点振速大于22号质点,说明迎爆侧质点振速分布规律沿轴向递减。根据近似约束条件,对各质点的振动速度进行分组对比可知,巷道周围各质点的最大振速随爆心距的增大而减小,爆心距越小的质点,越容易受到爆破振动的影响,但是巷道周围某些特殊位置的约束条件不同,会较容易受到爆破振动的影响。依照矿山巷道爆破振动安全允许标准为15～30 cm/s,为了安全起见,安全振速应取15 cm/s,除了最右侧巷道边墙右侧中部的8号质点振速为16.7 cm/s之外,模型中所取各质点振速均低于这个标准,符合安全准则,需对最右侧巷道边墙右侧中部加强支护,并适当减少炸药的用量。

3.2 巷道周围质点的位移分析

在爆破振动效应的影响下,各质点的合位移测试也是分析巷道变形规律的一个参量。运用LS-PrePost后处理软件导出各质点位移发生时间及爆心距曲线,如图9所示。

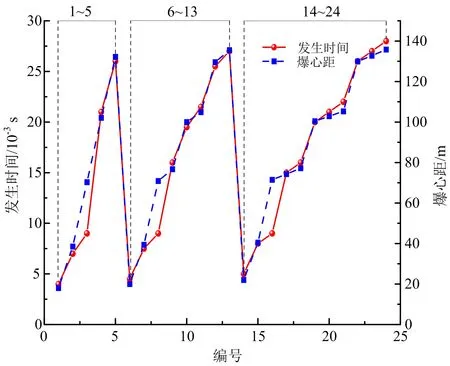
图9 各质点位移发生时间及爆心距Fig.9 The occurrence time of each particle displacement and the explosion center distance

由图9可知,所取的24个质点中,1～5号质点位于同一水平面,6～13号质点位于同一水平面,14～24号质点位于同一水平面,且爆心距逐渐增大,位移发生时间随爆心距的增大呈现递增趋势,说明爆破振动对质点位移的影响与爆心距相关,爆心距越小,位移发生时间越短。各质点的爆心距及爆破振动影响下产生的最大位移如图10所示。

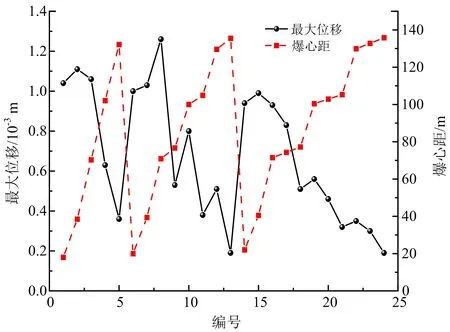
图10 各质点的爆心距及最大位移Fig.10 Blasting center distance and maximum displacement of each particle

由图10可知,3、4、5号质点分别位于模型右侧巷道、中间巷道、左侧巷道拱顶的中间位置,最大位移随爆心距的增大而减小。8～13号质点位于巷道边墙两侧的中间位置,绝对位移依次增大,但由于约束条件的不同,最大位移随着爆心距的增大,并非呈现递减趋势,而是间隔式递减。当约束条件相同的情况下,取8、10、12号质点为一组进行比较,9、11、13号质点为一组进行比较,结果显示,最大位移均随爆心距的增大而减小。16至24号质点位于巷道底板,根据约束条件,将其分成3组:16、19、22号质点为一组,17、20、23号质点为一组,18、21、24号质点为一组,可知当约束条件相同时,质点的最大位移依旧随爆心距的增大而减小。而且,在3个巷道边墙两侧的中部,迎爆侧的质点位移会明显大于背爆侧的质点位移,例如8号质点和9号质点,10号和11号,12号和13号,在巷道底板的18号点和19号点,21号点和22号点等。由此可知,在爆破振动开始之前,需要加强巷道迎爆侧的支护,保证爆破过程中的安全。尤其是巷道边墙两侧的中部位置,产生的影响较大。

4 现场收敛位移监测结果分析

随着煤矿爆破作业距离逐渐向巷道推进,将引起围岩力学性能变化,如围岩变形、巷道的稳定性受到极大威胁。巷道收敛量测对于了解围岩稳定情况、支护系统的作用效果以及支护系统与围岩之间的相互作用规律,监测矿山巷道稳定性、保障矿山安全生产均起着重要的作用,因此,巷道收敛量测作为井巷工程中的一项主要测试内容,不仅成为巷道掘进和采场回采过程中重要的安全监视手段,而且为调整支护设计和选定合理的支护时间及综合评价围岩稳定性提供科学信息。

现场采用数显收敛计对煤矿回风巷道围岩进行收敛观测,在巷道中设置观测断面共有8个断面,每个断面埋设3个测点,分别位于巷道拱顶中间和两帮距离巷道底板以上1.0 m处,用其观测巷道围岩在露天爆破振动作用下其围岩位移变化情况。为了掌握收敛随时间增长变化情况,将监测数据进行累计收敛值-监测时间作图,同时还绘制出单次收敛值-监测时间图,方便掌握巷道在某阶段时间的变化情况,如图11～14所示。

图11 巷道迎爆侧围岩监测截面收敛值变化趋势Fig.11 Trend of convergence value of surrounding rock monitoring section on blasting side of roadway

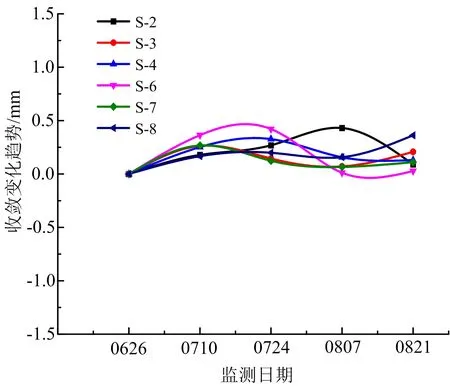
图12 巷道迎爆侧围岩监测截面单次收敛变化趋势Fig.12 Single convergence trend of surrounding rock monitoring section on blasting side of roadway

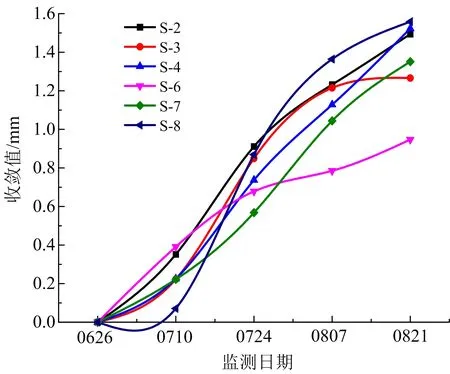
图13 巷道背爆侧围岩监测截面收敛值变化趋势Fig.13 Trend of convergence value of monitoring section of surrounding rock on back burst side of roadway

图14 巷道背爆侧围岩监测截面单次收敛变化趋势Fig.14 Single convergence trend of monitoring section of surrounding rock on back burst side of roadway

监测数据表明,相邻巷道围岩在原始支护作用下的水平收敛值变化依然较小,最大收敛值依然出现在监测截面中的S-2截面,两个多月时间内巷道两帮收敛值为0.97 mm;最小收敛值出现在监测截面中的S-7截面,两个多月时间内巷道两帮收敛值为0.57 mm;各截面的平均收敛值为0.80 mm,且各截面收敛变化率平均小于0.2 mm/d,该收敛速度变化不会导致巷道的破坏,因此可以判断该巷道围岩基本处于稳定状态。

从相邻巷道背爆侧围岩的收敛值监测数据表明,巷道背爆侧围岩的收敛值仍较小,收敛值最大出现在监测截面中的S-8截面,两个多月时间内巷道两帮收敛值为1.58 mm;收敛值最小出现在监测截面中的S-6截面,两个多月时间内巷道两帮收敛值为0.96 mm;各截面的平均收敛值为1.38 mm,且各截面收敛变化率平均小于0.2 mm/d,由此可以判断该巷道围岩基本处于稳定状态,该收敛速度变化不会导致巷道的破坏。

随着爆破区域逐渐靠近煤矿巷道,且爆破作业次数逐渐频繁,因此巷道收敛变化值逐渐增大,在今后巷道近区进行露天爆破作业时应加强爆破振动的控制,严格按照近区减振爆破方案实施爆破作业,与此同时应加强巷道稳定性变化的监测,防止巷道失稳而发生安全事故。

5 爆破振动模拟中合速度衰减方程

对质点的振速和位移分析之后,运用萨道夫斯基公式[16]对振动模拟中合速度的衰减方程进行计算。

萨道夫斯基提出的经验公式如下:

v=K(Q1/3/R)α

(1)

式中:v为质点振动速度,cm/s;Q为炸药量,kg;R为质点爆心距;K是介质相关系数;α为衰减系数。

以比例距离跟质点的最大振速为变量,依据萨道夫斯基公式及回归原理找出合速度v跟比例距离R/Q1/3的值,反演得到K、α的值。采用最小二乘法原理对公式(1)进行转化换算,得K、α的计算公式分别如下:

(2)

由于考虑到约束条件的影响,应该选取同一约束条件的质点最大振速代入上述公式中,测试选取右侧巷道边墙中间位置质点的最大振速代入公式(2),其中xi=ln(Q1/3/R),yi=lnv,参数反演结果如表1所示。

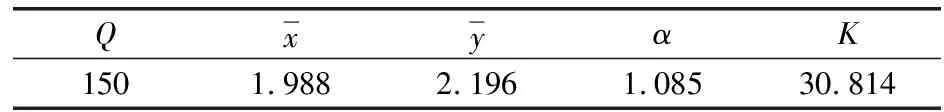
表1 反演参数

由此得到本次模拟爆破振动测试合速度的衰减方程为

(3)

6 结论

1)巷道周围各质点的最大振速随爆心距增大而减小,距离爆源越近的质点,越容易受到爆破振动的影响。右侧巷道边墙中部质点振速高于标准,需加强支护,适当减少炸药的用量,或者增大爆心距。

2)位于同一水平面的质点,位移发生时间随爆心距的增大而增大。位于右侧巷道、左侧巷道拱顶中部的质点,其位移随爆心距的增大而减小。巷道两侧边墙中部的绝对位移依次增大,但由于约束条件的不同,最大位移随着爆心距的增大,并非呈现递减趋势,而是间隔式递减。当约束条件相同的情况下,质点的最大位移依旧随爆心距的增大而减小。

3)收敛监测结果表明爆破振动作用对巷道的稳定性造成的影响仍处于稳定变形阶段,不会导致巷道的破坏。

4)采用最小二乘法回归原理反演得到煤矿爆破的萨道夫斯基公式中的K值及α值分别是30.814及1.085,计算得到的经验公式对于预测露天矿爆破中质点振速以及爆破地振波对巷道的影响具有一定的参考意义。