针电极曲率半径对微间隙空气放电击穿特性的影响
伍凤娟,刘树林,王党树
(西安科技大学 电气与控制工程学院,陕西 西安 710054)
0 引 言
开关变换器发生故障(如输出短路和内部分断放电)可能会引燃爆炸性气体。根据国家强制性标准要求,本安开关变换器须在IEC安全火花试验装置上进行短路、分断放电爆炸性试验,检测其本安性能[1-2]。由于本安开关变换器输出短路放电可以等效为电容短路放电,该放电属于低压微间隙放电。不同电极结构通过影响微间隙放电机理提供不同的本安判据,该判据为大功率本安开关变换器设计提供了理论参考。因此,基于IEC安全火花试验装置的电极结构建立二维针-板电极几何模型,探究电场强度、曲率半径、电极间距与击穿电压之间的关系,对开关变换器电容输出短路放电机理研究及大功率本安开关变换器设计意义重大。
目前对电极结构的研究多集中在阴极表面微凸起及场增强因子[3-4],主要通过曲线拟合、数学模型等研究场增强因子数值计算方法[5-8]以及通过建立相关模型研究微凸起几何形状对间隙击穿特性关键参数的影响机制[9-10]。由于电极几何形状尤其是曲率半径决定间隙电场分布,而电场强度是衡量介质能否被击穿的关键因素,因此,部分学者基于场增强因子,研究了曲率半径对电场强度分布的影响。何彦良等建立了SF6/N2混合气体二维轴对称针-板几何模型,得出针电极曲率半径决定电场的畸变程度,会影响针尖附近的电场及带电粒子的漂移扩散[11];王佳通过对场畸变型间隙电场分布进行研究,得出场增强因子在间距较小时,受曲率半径的影响大,且曲率半径变化比电极间距变化对场强的影响更为显著[12];MA等通过对交直流电压下小曲率电极电晕起始特性进行试验研究,得出小曲率电极下起晕电压受电极间距的影响大于曲率半径的影响[13];LI等通过对绝缘油流注放电进行数值模拟,得出曲率半径影响针电极电场分布,小曲率半径增强电场,产生更多的空间电荷,使电场更易发生畸变,利于流光的正向传播[14];何寿杰等研究了低气压氧气环境中针-板放电结构产生的Trichle脉冲放电特性,其中电极间距为1 cm,电极曲率半径为0.1 mm[15];柴钰等建立了常温常压下N2-O2混合气体在微米间隙-纳米尖端场域的二维空间放电模型,通过分析空间电子输运机制阐明了该场域下空间放电的动态发展过程[16]。
上述研究均基于高压、长间隙放电理论,而基于IEC安全火花试验装置的放电则属于低压、微间隙放电,该领域放电机理研究鲜有报道。王党树等基于粒子法建立了3种不同电极模型,阐述电极结构对电场分布的影响,得出相同情况下,锥形电极击穿电压最小且相对于球形和柱形电极最易击穿[17],但并未研究曲率半径对击穿场强的影响机制。常泽洲等利用PIC/MCC法建立了二维物理模型,对微间隙击穿过程的电场分布、带电粒子分布及击穿路径进行了研究[18],但未对曲率半径与击穿电压之间的关系进行定量计算。
因此,为探究低压、微间隙条件下电极曲率半径对击穿特性的影响,综合考虑场增强因子β及曲率半径,采用坐标变换法定量计算针尖处非均匀电场强度。基于流体-化学动力学理论建立了微米级间隙下二维轴对称针-板电极几何模型,模拟常温常压不同针电极曲率半径下空气负直流放电过程,通过正负离子、电子的连续性方程与泊松方程耦合研究针尖处电场分布情况,进一步揭示低压、微间隙放电机理,最后通过微纳程控放电试验平台对试验进行了验证。
1 曲率半径及场增强因子协同作用下非均匀电场强度数值计算
非均匀电场强度的定量计算对于进一步探究电场中带电粒子运动、揭示放电规律具有重要意义[19],尤其是低压微间隙放电领域非均匀电场强度的数值计算。由于电场计算的基本问题是在适当边界条件下求取满足拉普拉斯方程的电势值,而坐标变换法即把拉普拉斯方程假定为变量分离的形式去求解的一种方法,对于旋转椭球面、旋转双曲面依靠适当选取参数即可根据电极形状计算电场强度。因此,建立旋转椭球坐标系(ξ,η,θ),采用坐标变换法定量计算综合考虑场增强因子β及曲率半径的针尖处非均匀电场强度[20]。图1为针-板电极旋转椭球坐标系1/4剖面。

图1 旋转椭球坐标系1/4剖面Fig.1 1/4 cross-section of rotating coordinate system
旋转椭球面方程为
(1)
与旋转椭球面正交的旋转双曲面方程为
(2)
直角坐标系中有
(3)
式中θ为方位角,且0≤θ≤2π。
对其进行坐标变换可得
(4)
针-板电极中电势φ满足拉普拉斯方程为
(5)
为求解式(5),采用分离变量法,将其分解为仅含坐标量为常数项与另一函数的乘积形式,最终通过求解勒让德多项式得出针-板电极系统中电势的通解。
设针电极表面以η=η0的旋转双曲面予以逼近,板电极与η=0的旋转双曲面相重合,针-板电极间距为d。此时,该针-板电极系统可归结为以下边值问题。
(6)
根据边界条件及上述求出的通解形式推导得
(7)
针-板电极体系下位于针尖处的最大场强为

(8)
式中η0取决于针电极实际形状。
为简化分析,将针电极尖端近似为半径为r的局部球面(假设与η=η0在尖端处的曲率半径相等),根据旋转双曲面方程,空间曲面曲率半径计算式为
(9)
(10)
由φ0=u0,利用式(10)且考虑r≪d则有
(11)
从式(11)可知,不同针电极曲率半径会改变电场分布使得电场发生畸变。相同间距下,击穿电压随曲率半径的减小而减小,曲率半径越小,电场畸变越严重。由于阴极表面存在微凸起,会增强电极表面局部电场,因此引入场增强因子描述不同曲率半径下电场畸变程度。此外,局部电场大小影响场发射电流,而曲率半径通过影响场发射电流大小来影响击穿电流。场发射电流密度可由Fowler-Nordheim公式计算,其速度符合Maxwell分布,计算式为
(12)

场增强因子β(6≤β≤30)[21]与微凸起高度h、曲率半径r、电极间距d之间关系式为[22]
(13)
(14)
从式(11)~式(14)可知,击穿场强受曲率半径和场增强因子共同影响,场增强因子越大,击穿场强越小,击穿电压越低。此外,曲率半径和电极间距共同影响电场畸变程度,且两者对电场强度的影响存在一个临界间距,不同间距下,曲率半径对电场畸变的影响程度不同。以下将从数值仿真及试验两方面共同验证上述理论分析。
2 低压微间隙针-板电极放电模型
2.1 针板电极几何模型
基于流体-化学动力学理论采用有限元分析软件建立如图2(a)所示的简化空气二维轴对称针-板几何模型。其中,气压为1 atm,温度为293.15 K,针-板电极间距为8 μm,针电极曲率半径r分别设置为0.1 μm、0.5 μm、1 μm,针电极通过R、C电路(R=1 kΩ,C=1 pF)接负电压(-200 V),平板电极接地。由于针电极曲率半径极小,电极尖端处电场强度梯度非常大,因此该区域附近采用极细化网格,具体针电极边界网格剖分遵循最小单元尺寸小于最窄宽度的十分之一原则,具体参数为:最大单元尺寸为0.03 μm,最小单元尺寸为0.001 μm,如图2(b)所示。
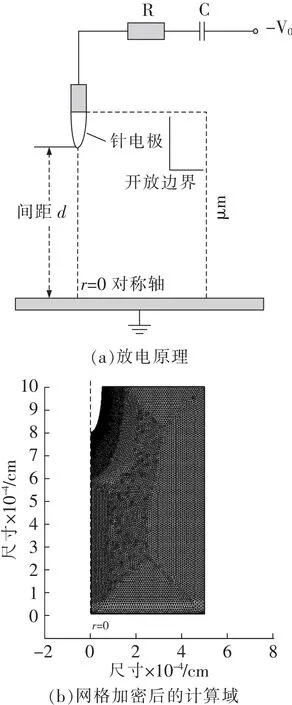
图2 针-板电极模型示意Fig.2 Sketch of needle-plate electrode
2.2 控制方程
流体模型主要包括:电子连续性方程、电子能量守恒方程、动量守恒方程以及泊松方程。电子连续性方程用于计算电子数密度,电子能量方程和动量守恒方程用于计算电子能量系数与离子动量系数,并分别将结果传递给连续性方程,最后通过泊松方程进行耦合[23]。
电子连续性方程为

(15)
Γe=μeneE-Dene
(16)
式中ne为电子数密度,m-3;Γe为电子通量,1/(m2·s);Se为源项,表示等离子体微观反应模型产生电子的净速率,m-3·s-1;μe和ne分别为粒子的迁移率和扩散率,cm2/(v·s);D为粒子的扩散系数;E为电场强度,V/m。
电子能量守恒方程为
(17)
式中KB为玻尔兹曼常数;ψe为电子能量通量,eV;me为电子质量,kg;ne为电子数密度;M为气体平均分子质量;vel为弹性碰撞频率,Hz;Tg为气体温度,K;ri为第i次反应的速率;Δεi为由非弹性碰撞引起的能量损失。
动量守恒方程为
式中m为电子质量;u为电子漂移速度;P为电子压力张量,Pa;vm为电子动量碰撞频率。
泊松方程为
(19)
式中φ为电势,V;ε0为真空介电常数;εr为气体相对介电常数;q为电荷量,C;zi为粒子带电量。
在针电极和板电极处,电子通量Γe和电子能量ψe满足以下边界条件
(20)
ξ(Γt·n)
(21)

对于求解域边界,所有粒子及电势满足
(22)
2.3 等离子体化学反应
研究针电极曲率半径对空气放电击穿特性的影响时,不涉及某一种带电粒子的具体反应及变化过程,因此采用简化的空气反应,统一以物质A作为代替(即物质A可以电离成正离子A+,也可以吸附电子变成负离子A-)。表1中“-”表示对该参数无需进行单独设置,碰撞电离与附着反应的反应速率可以直接采用汤森系数。

表1 等离子体化学反应
合适的初始粒子数密度可以提高收敛性,且不会改变仿真特性。设置初始条件为:电子初始数密度为1×1010m-3,离子数密度为1×1016m-3,初始正负离子数密度遵循电中性原则。简化的空气放电等离子体化学反应见表1。
2.4 仿真结果分析
放电过程受电极影响主要体现在以下两方面:一是带电粒子与电极表面碰撞发生表面反应并伴随二次电子发射;二是放电过程中电极表面形成电荷积聚,导致电场分布不均匀。二者共同作用,推动放电过程持续发展[26]。
电子是外加电场与重粒子能量传递的主要载体[27],从电子数密度的变化图中可直接看出放电的发生、发展过程;电场强度是判断该模型是否放电的重要依据,是电极间距与击穿电压之间的纽带。因此,为了进一步研究曲率半径、电极间距与击穿电压之间的关系,揭示微间隙放电机理,对固定电极间距d=8 μm处不同时刻、针电极曲率半径r分别为0.1 μm、0.5 μm、1 μm时电子密度与电场强度分布进行仿真分析,结果如图3所示。

图3 不同时刻、不同曲率半径下电子密度分布及针尖处场强分布Fig.3 Distribution of electron density and electrical field intensity at needles under different radius of curvature at various moments
t1=0.1 ns时刻,从图3(a)可以看出,针电极曲率半径r分别为0.1 μm、0.5 μm时,针尖处电场强度已至105V/m,此时虽未放电,但电子数密度已开始增加,隐约可见电荷在阴极表面出现积聚现象。随着电场强度的增大,电极表面电荷积聚效应加剧,尖端处电子数密度不断增加,从而使电子与气体分子碰撞加剧,阴极表面开始发生表面反应且产生二次电子发射,曲率半径较小的电极尖端处电场强度迅速增107V/m,由于阴极表面存在场增强因子,此电场强度足以击穿空气间隙促使气体发生放电。而同一时刻下曲率半径越大,阴极表面电子数密度增加越缓慢,电场强度亦未达到放电阈值,如图3(b)、图3(c)所示。随着放电时间的推移,尖端处强电场形成的空间电离速率不断加强,使得电子数密度迅速增加,如图3(d)所示,t4=80 ns时,r1、r2对应的电子数密度最大值分别为5×1015m-3、3×1015m-3,电场强度最大值分别为-3.7×107V/m、-1.48×107V/m;而r3对应的最大电子数密度为2×1013m-3,电场强度最大值为-8.96×106V/m。由此可见:曲率半径越小,同一时刻电子数密度增加越快,电极尖端电场强度越大。随着电场强度趋于稳定,电子数密度维持不变,如图3(e)所示,针尖处形成的电晕逐渐向阳极移动,这是由于随着阴极附近电子密度增加,由电子附着反应产生的负离子不断累积,电子在阳极因复合而消失的速率增大。此外,由于空间电荷效应会削弱电极尖端附近电场强度,进而抑制场发射过程,最终使得电极尖端电子密度向阳极移动,直至正负离子的产生与消耗达到动态平衡。
图4为放电达到稳定状态时轴向电子数密度分布,可以看出曲率半径越小电子数密度越大,且电子数密度的峰值位于距离阳极1 μm附近的鞘层区,这是空间电荷效应和场增强因子共同作用的结果。

图4 轴向距离电子数密度分布Fig.4 Distribution of electron density in axial direction
图5为不同曲率半径下电场强度随时间变化曲线。从图5可以看出,t<10 ns时,由于电子数密度小,气体电离程度低,电荷仍处于不断积聚状态,曲率半径对放电的影响不太明显;t≥10 ns时,曲率半径越小,电场强度变化越快,直至t=80 ns时,电场强度趋于稳定,且随着放电过程的推进,电极曲率半径越小,电场强度越大,放电时间越短。

图5 不同曲率半径电场强度随时间的变化Fig.5 Variation of electric field intensity with time under different radius of curvature
由上述分析可知,当电极间距d=8 μm时,场致发射为主,曲率半径对电场强度的影响较大。以下将采用程控微纳间隙放电试验平台,通过改变电极间距获取击穿电压与曲率半径之间的关系。
3 试验验证
3.1 试验平台
采用程控微纳间隙放电试验平台进行试验验证,系统框图如图6所示[28]。主要包括:程控系统、光学平台、电源、示波器、探头、源表、计算机。程控系统通过控制步进电机移动针电极向平板电极靠近,最小步进为10 nm;光学平台用于减小误差、提高测量精度;试验电源为Itech IT8818可调直流电源;示波器为采样频率2.5 GHz的RIGOL DS4024,主要用于采集极间电压和电流信号;源表为Keithley 2634B用于测量回路中的电流值(电流测量范围为0.1 nA~10 A),如图7所示。
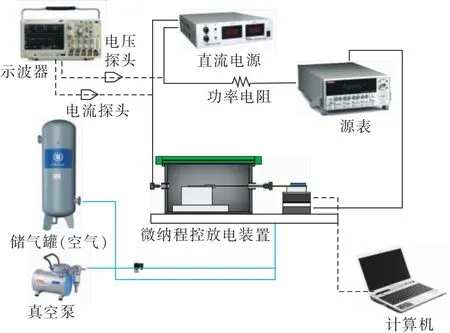
图6 程控微纳放电试验系统Fig.6 Test system of program-controlled micro-nano discharge

图7 程控微纳放电试验平台Fig.7 Test platform of program-controlled micro-nano discharge
具体试验过程中给阳极施加1 V电压,将阳极作为移动电极逐步向阴极靠近,直至电流发生突变(判断电极短路),此时立即停止移动阳极并将该电压撤去,记录此位置为零点,随后将电极回移直至试验所需电极间距(d1=6 μm、d2=8 μm、d3=10 μm)。选取不同曲率半径下的试验电极分别对不同极距下击穿电压进行测量,并用示波器采集电压、电流波形。
3.2 试验结果分析
为了说明曲率半径、电极间距与击穿电压之间的关系,基于微纳程控放电试验平台进行了相关试验。通过该平台测得电极间距从1~15 μm变化时击穿电压,多次重复试验取平均值并对其进行拟合,如图8所示。从图8可以看出,当d≤8 μm时,随着电极间距增大,击穿电压也逐渐增大,该间距下测得的曲线偏离帕申曲线,表明该间距下的放电机制为场致发射;d>8 μm时,击穿曲线与帕申曲线高度一致,表明该间距下放电机制为汤森放电。此外,相同电极间距下,曲率半径越小,击穿电压越小。
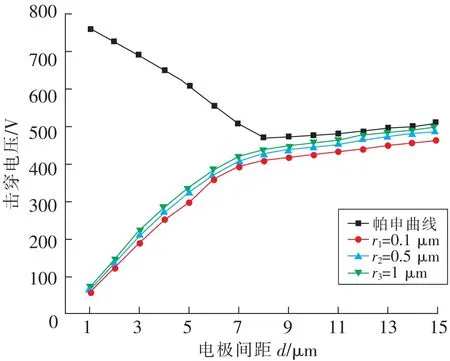
图8 不同曲率半径击穿电压与电极间距曲线Fig.8 Electrode space curves of breakdown voltage under various radius of curvature
图9为固定曲率半径、不同电极间距下击穿电压随时间变化的实测波形。从图9可以看出,d=6 μm和d=8 μm时,电压下降2次最终降到维持电压,这是由于电极两端电压达到一定值后,阴极表面存在场增强因子,一旦电场强度达到107V/m就会引起场致发射,从而击穿间隙诱导放电。随着放电持续进行,电极尖端温度升高,极间金属液化形成金属液桥,使得极间电压迅速降低直至接近于零,这说明场致发射在该放电过程中起主导作用;而当d=10 μm时,电压直接降至维持电压,说明场致发射对该放电过程的影响很小,电极间距变化对电场强度的影响远小于针电极曲率半径对电场畸变的影响,且该试验结果与仿真结果十分吻合。
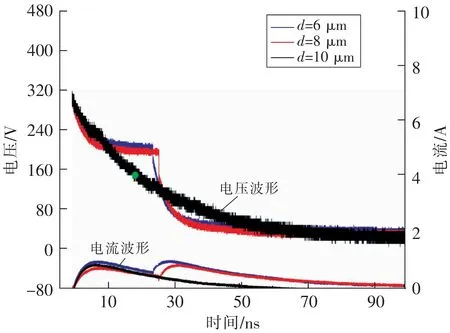
图9 不同电极间距下电压和电流波形Fig.9 Waveforms of voltage and current at different electrode spaces
4 结 论
1)结合场增强因子定量分析了低压微间隙下电场强度、曲率半径、电极间距与击穿电压之间的数学关系,得出针电极曲率半径和场增强因子共同影响击穿电场,场增强因子越大,击穿场强越小,击穿电压越低;相同电极间距下,击穿电压随曲率半径的减小而降低。
2)建立了二维轴对称针-板电极几何模型,分析了曲率半径对电子数密度、电场强度的影响规律,得出同一时刻,曲率半径越小,电子数密度增加越快,尖端处电场强度越大,越容易放电。
3)曲率半径和电极间距共同影响电场分布,电极间距d≤8 μm时,曲率半径对畸变电场的影响较大;d>8 μm时,电极间距对畸变电场的影响较大,二者共同作用最终影响微间隙放电机理。为大功率本质安全开关变换器设计提供了理论参考。

