水流作用下裂隙内沉积颗粒起动临界流速研究

胡东亮,问小江,郑玲娜,刘应科,方飞飞,王凤超

(1.贵州盘江精煤股份有限公司,贵州 盘江 553500;2.中国矿业大学 安全工程学院,江苏 徐州 221116;3.中国矿业大学 低碳能源与动力工程学院,江苏 徐州 221116)

0 引 言

瓦斯灾害是限制矿井安全高效生产的重要因素[1-3]。瓦斯抽采是防治瓦斯灾害的根本措施[4-7],其中,煤岩内裂隙的畅通性是影响瓦斯抽采效率的重要基础[8-10]。然而,瓦斯抽采气流中会不可避免地携带一些煤岩颗粒,这些颗粒在运移过程中会沉积在裂隙底部并形成颗粒沉积床,甚至完全堵塞裂隙,增大了裂隙的局部阻力系数,严重影响瓦斯抽采效果[11-13]。该问题在采动裂隙场中的离层裂隙内更加突出。在离层裂隙内,由于瓦斯流动方向和煤岩颗粒沉积方向不一致,使得颗粒悬浮运移的难度系数增大,颗粒更容易在裂隙内形成沉积床[14-15]。

水力冲刷技术是解决颗粒阻塞裂隙的有效手段[8]。该技术的原理为通过向裂隙注入大量清水,利用清水的冲刷作用减少裂隙内的沉积颗粒数量,进而提高阻塞裂隙的畅通性。可见,裂隙内注水量是影响水力冲刷效果的关键因素。然而由于对裂隙内颗粒起动临界流速变化规律不清楚,工程上水力冲刷工艺的注水量往往根据技术人员的经验确定,这样会造成极大的水资源浪费[16]。为优化阻塞裂隙的水力冲刷工艺参数(注水量),亟需开展裂隙内沉积颗粒起动临界流速的变化特性研究。

在水流中颗粒起动方面,很多研究者已开展了大量研究。汤碧辉等建立基于滚动起动的颗粒起动数学模型,研究了粘性泥石流中大颗粒的起动特性[17]。蔡蓉蓉等推导明渠流下颗粒临界起动流速的半经验公式,并通过物理试验表明该公式具有良好的适用性[18]。赵东伟等建立颗粒滚动的力矩平衡方程,推导了考虑颗粒起动随机性的临界流速公式[19]。宋洵成等建立颗粒运移临界流速的数学模型,提出了倾斜井眼临界环空返渣流速的计算方法[20]。陈烨等基于颗粒随机分布特征建立颗粒起动流速数学模型,研究了钻柱偏心度、颗粒密度等因素对颗粒起动临界流速的影响[21]。LAN等运用水动力理论,建立煤粉颗粒起动的力学模型,提出排采阶段的临界排水速度,并对不同情况下的煤粉产出量进行了预测[22]。綦耀光等建立裂隙内煤粉脱落、运移和阻塞的孔隙度和渗透率模型,得到了裂隙内煤粉颗粒发生滚动的临界流速[23]。马子普等以指数律流速分布公式,基于Einstein假设推导得到了同时适用于明渠流的统一的非黏性泥沙颗粒起动流速公式[24]。ZEEHAN和SUBHASISH分析无黏性颗粒在紊流光滑区、过渡区和粗糙区的受力特征,并以滚动为起动形式分析了颗粒在不同流态下的起动规律[25]。然而,目前对裂隙内颗粒起动临界流速的研究还很不充分。

为了优化阻塞裂隙的水力冲刷工艺参数,采用物理试验和理论分析相结合的方法研究裂隙内沉积颗粒的起动方式以及颗粒粒径、流体密度和裂隙高度对裂隙内颗粒起动临界流速变化特性的影响,为提升采动裂隙的疏通性提供理论指导。

1 试验方法

1.1 试验颗粒

采用425～1 400 μm焦炭颗粒作为试验颗粒。颗粒密度为1.8 g/cm3,部分颗粒形状如图1所示。

图1 颗粒形状Fig.1 Particle shape

根据标准筛分类标准,将425～1 400 μm颗粒共分为7组,见表1。为了便于分析颗粒起动规律,后续研究中将各组颗粒的粒径算术平均值作为粒径值。

1.2 试验系统

试验系统主要由水流发生单元、裂隙单元和数据采集单元组成,如图2所示。

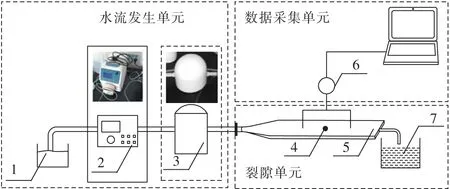
1-水箱;2-蠕动泵;3-阻尼器;4-沉积颗粒;5-矩形裂隙;6-压差传感器;7-颗粒收集盒图2 试验系统Fig.2 Experiment system

水流发生单元主要由水箱、蠕动泵和脉冲阻尼器组成。蠕动泵为齐力BF600-蠕动泵,能够实现无极调节水泵流量,流量可调范围为0～1 000 mL/min。脉冲阻尼器能够确保进入裂隙单元的水压恒定,试验中水压均为0.25 MPa。

裂隙单元为由亚克力材料制成14 mm×2 mm(宽×高)的矩形通道。整个通道分为充分发展段、试验段和出口段,总长310 mm。充分发展段总长70 mm,试验段总长200 mm,出口段总长40 mm。数据采集单元为压差传感器,压差传感器测点布置于试验段的进、出口位置,测点间距200 mm。

1.3 试验设计

根据试验目的,共开展11组裂隙内沉积颗粒起动试验。其中11组试验被分为粒径组和流体密度组。粒径组编号为1#～7#,粒径组中流体密度均设定为997 kg/m3。流体密度组编号为2#和8#～11#,流体密度组颗粒粒径均为925 μm。裂隙内沉积颗粒起动试验参数见表2。

表2 水力冲刷试验参数

1#～7#的试验工况中流体为水,8#～11#的试验工况中流体为不同浓度的丙三醇溶液,丙三醇浓度依次为0.03 g/mL、0.06 g/mL、0.11 g/mL和0.19 g/mL。

1.4 试验步骤

裂隙内沉积颗粒起动试验步骤如下:

1)开启蠕动泵向裂隙单元内注水至满管状态,然后关闭蠕动泵;

2)将单个颗粒放置在试验段进口位置处;

3)开启蠕动泵,多次缓慢增大蠕动泵流量直至颗粒发生起动,并运移出裂隙单元。随后关闭蠕动泵,完成一次颗粒起动试验。值得注意的是,蠕动泵单次增大流量不超过5 mL/min(流速0.3 cm/s);

4)为减小试验误差,回收步骤3)中的颗粒,并进行重复试验,重复试验次数为3次。

2 采动裂隙内沉积颗粒起动方式

随着裂隙内水流速度的增大,沉积颗粒经历了静止、间歇运动和持续运动3个阶段。前人的研究中颗粒起动状态主要通过视觉观察来定义[26-28]。为了定量分析沉积颗粒的起动规律,将沉积颗粒由间歇运动状态转变为持续运动状态的临界状态定义为颗粒起动临界状态。

颗粒形状对颗粒起动临界状态的起动方式具有重要影响。由第1.1小节分析可知,颗粒形状具有极强的不规则形,因此尽管颗粒粒径相同,但颗粒起动方式不完全相同。以925 μm颗粒起动试验为例(2#),不同形状颗粒的起动方式如下。

2.1 近圆颗粒

根据流体力学知识可知,颗粒在水中主要受到曳力作用[29-30]。如图3所示[31],由于颗粒起动过程中近圆颗粒与裂隙底面为点接触,曳力能够以该接触点为转动中心产生转动力矩。因此当近圆颗粒发生起动时,颗粒的起动方式为滚动。

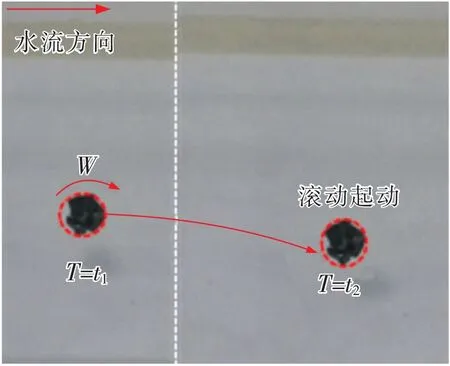
图3 近圆颗粒的起动方式Fig.3 Incipient behavior of near-circular particles

2.2 椭球形颗粒

从图4可以看出,颗粒起动过程中,椭球形颗粒与裂隙底面为线接触,颗粒所受曳力能够以该接触线为转动轴产生转动动力矩。因此与近圆颗粒起动方式类似,椭球形颗粒发生起动时,颗粒的起动方式为滚动。

图4 椭球形颗粒的起动方式Fig.4 Incipient behavior of ellipsoidal particles

此外,试验中可以观察到,椭球颗粒在滚动过程中,颗粒还会以颗粒长轴中点为转动点发生自转,如图5所示。这是因为当颗粒长轴与水流方向的夹角小于90°时,受颗粒右侧尾涡影响,颗粒左侧的流体作用力大于颗粒右侧的流体作用力,因此前者以颗粒长轴中心为转动点产生的力矩大于后者,促使颗粒发生自转。

图5 椭球形颗粒长轴转动示意Fig.5 Schematic diagram of the rotation of the long axis of ellipsoidal particles

当颗粒长轴与水流流动方向垂直后,颗粒将不再自转,并保持该姿态滚动出裂隙。这是由于当颗粒长轴垂直于流体流动方向时,颗粒左右两侧流体的作用力近似相等,二者以颗粒长轴中点为转动点的力矩达到平衡状态。

2.3 扁平颗粒

如图6所示,颗粒起动过程中,扁平颗粒与裂隙底面为面接触。因此,当水流对颗粒的曳力大于颗粒与裂隙的滑动摩擦力,颗粒以滑动方式起动。

图6 扁平颗粒的起动方式Fig.6 Incipient behavior of flat particles

3 颗粒起动临界流速的变化特性

为便于分析,将颗粒起动临界状态下对应的裂隙内流体速度定义为颗粒起动临界流速。

3.1 粒径对颗粒起动临界流速的影响

颗粒形状对颗粒起动方式具有重要影响,且试验中颗粒为随机采样,因此同一粒径组下不同形状的颗粒起动临界流速仍具有较大差异性。为了进一步减小粒径组(1#～7#)的试验误差,同一粒径下随机选取50个颗粒,并测试每个颗粒的颗粒起动临界流速。图7中纵坐标代表在50组试验中颗粒起动临界流速在某一范围的出现频率。测试结果表明同一粒径下不同形状颗粒的起动临界流速服从正态分布(图7)。

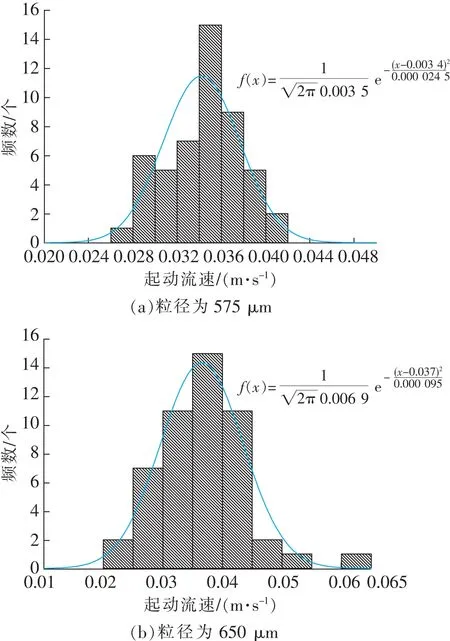
图7 颗粒起动临界流速测试结果Fig.7 Test results of threshold velocity of particle incipient motion

某一粒径下的颗粒起动临界流速应对该粒径下不同形状的颗粒具有普遍适用性。因此将能使同一粒径下90%以上的颗粒发生起动的流体速度定义为该粒径对应的颗粒起动临界流速。值得注意的是,某一粒径对应的颗粒起动临界流速采用统计学方法计算得到,具体计算方法如下:

1)测试某一粒径下形状不同的50个颗粒的起动临界流速;

2)拟合得到该粒径下颗粒起动临界流速正态分布曲线及其概率密度函数;

3)将步骤2)得到的颗粒起动临界流速正态分布转化为标准正态分布;

4)查询标准正态分布表,得到Y值90%对应的X值,X值为该粒径对应的颗粒起动临界流速。

不同粒径颗粒的起动临界流速如图8所示,从图8可以看出,颗粒起动临界流速随颗粒粒径的增大呈对数增大的趋势,且随着颗粒粒径的增大,颗粒起动临界流速的增长速率逐渐减弱。

此外,当裂隙内沉积颗粒发生起动时,裂隙内雷诺数为73.76～292.06,此时裂隙内流体流态为层流[14]。因此1#～7#试验中颗粒均在层流状态下发生起动。

3.2 流体密度对颗粒起动临界流速的影响

为降低颗粒粒径和形状对流体密度组的试验误差,流体密度组试验工况使用的颗粒均为同一颗粒。流体密度对应的颗粒起动临界流速为3次重复试验的平均值。

颗粒起动临界流速随流体密度的变化如图9所示。从图9可以看出,颗粒起动临界流速随流体密度的增大而减小,当流体密度由997 kg/m3提高至1 041 kg/m3时,颗粒起动临界流速由4.35 cm/s减小至2.61 cm/s,降低幅度高达40%。曳力是促使裂隙内颗粒发生的起动的重要动力。对于同一颗粒而言,提高流体密度能够显著提高水流对颗粒的曳力,使得颗粒在更小的流速下发生起动。

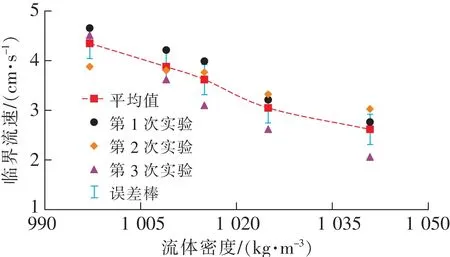
图9 颗粒起动临界流速随流体密度的变化Fig.9 Variation of threshold velocity of particle incipient motion with fluid density

综上所述,提高流体介质的密度能够在减少水力冲刷工艺中用水量的同时,有效促使粒径较大的颗粒在裂隙内发生起动,提高水力冲刷工艺的实践效果。

流体密度组试验中颗粒发生起动时,裂隙内雷诺数为50.12～121.26,表明试验中颗粒仍均在层流状态下发生起动。

3.3 裂隙高度对颗粒起动临界流速的影响

采用理论分析的方法研究裂隙高度对颗粒起动临界流速的影响。根据第3.1小节和第3.2小节分析可知,裂隙内沉积颗粒均是在层流状态下发生起动的。

水力冲刷工艺中裂隙内水流是在压力梯度驱动下流动的,且在实际施工过程中该压力梯度基本保持恒定。考虑到实际中裂隙在宽度方向的延展性,同时忽略裂隙表面粗糙度的影响,将裂隙内流动简化为常压力梯度下2个无穷大平板内的流动。如图10所示,假设裂隙内流动为2个无穷大平板之间的层流流动,上下平板的坐标分别为y=±h,坐标原点位于中心位置。流场流动方向为x方向,平板在x和y方向无线延展。

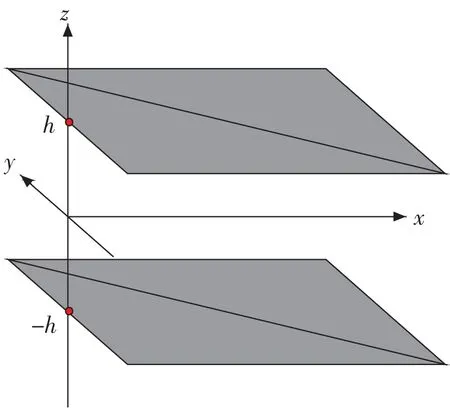
图10 裂隙物理模型Fig.10 Fracture physics model

根据流体力学知识可知,上述裂隙内的流动为泊肃叶流动,则裂隙内流速分布公式为[32]

(1)

式中 ΔP/L为驱动裂隙内水流流动的压力梯度,N/m3;h为裂隙高度H的一半,m;μ为水流的动力粘度,Pa·s;z为裂隙内任意一点在重力方向的坐标,m。

裂隙内的平均流速计算公式为

(2)

式中um为裂隙内水流平均流速,m/s。

水流作用下裂隙内颗粒发生起动时,本质上仅颗粒表面流速对颗粒起动是有效的。在此基础下,提出了颗粒起动过程中水流有效作用流速ul,并在裂隙内流速分布公式基础上,通过积分的方法得到了该有效作用流速。

为了便于分析,忽略颗粒形状对颗粒起动的影响,将颗粒简化为圆球模型。如图11所示,以颗粒球心O′为圆心建立球坐标系。

图11 球坐标系Fig.11 Spherical coordinate system

颗粒表面上任一点P可表示为P(R,θ,φ),由公式(1)可知,颗粒表面上P点的流速分布方程为

(3)

则颗粒起动过程中水流有效作用流速ul计算公式为

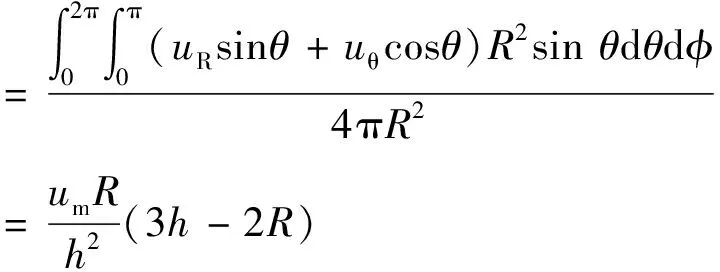
(4)

式中R为颗粒半径,m。

公式(4)可化简为

(5)

式中H为裂隙高度,m;Dp为颗粒粒径,m;um为裂隙内水流平均流速,m/s。

根据公式(5)可知,当颗粒粒径和裂隙内平均流速一定时,作用于颗粒表面的有效作用流速将随裂隙高度的增大而减小。

为了便于分析,将颗粒起动临界状态下作用于颗粒表面的水流有效作用流速定义为临界有效作用流速。此外,颗粒起动临界状态下裂隙内水流平均流速即为颗粒起动临界流速。则根据公式(5)可知,临界有效作用流速与颗粒起动临界流速、颗粒粒径和裂隙高度直接相关。

颗粒起动应满足的基本条件为水流作用于颗粒的有效作用流速大于临界有效流速,且颗粒粒径一定时,临界有效作用流速是固定的。

当颗粒粒径和裂隙内平均流速一定时,作用于颗粒有效作用流速随裂隙高度的增大呈减小的变化规律(式(5))。这将意味着颗粒粒径一定时,随着裂隙高度的增大,裂隙内应提供更高的平均流速以满足沉积颗粒发生起动的基本条件。因此,颗粒临界起动流速将随裂隙高度的增大而增大。当水力冲刷工艺运用至裂隙发育的地带时,应该适当提高水力冲刷工艺的注水量,促使沉积颗粒发生起动,提高堵塞裂隙的水力冲刷工艺效果。

4 结 论

1)颗粒形状对颗粒起动临界状态的起动方式具有重要影响。扁平颗粒主要以滑动方式起动,而近圆颗粒和椭球形颗粒的起动方式为滚动。除此之外,椭球形颗粒在滚动的同时还将绕颗粒长轴中心自转,直至自转至颗粒长轴与水流流动方向垂直。

2)裂隙内颗粒起动均发生在层流状态下。颗粒起动临界流速随颗粒粒径的增大呈对数增大的变化趋势。颗粒起动临界流速随流体密度的增大而减小,因此提高流体介质密度是降低颗粒起动临界流速的有效手段。裂隙内颗粒起动均发生在层流状态下。颗粒起动临界流速随颗粒粒径的增大呈对数增大的变化趋势。颗粒起动临界流速随流体密度的增大而减小,因此提高流体介质密度是降低颗粒起动临界流速的有效手段。颗粒起动临界流速随裂隙高度的增大而增大。因此,当水力冲刷工艺运用至裂隙发育的地带时,提高水力冲刷工艺的注水量是提高堵塞裂隙的水力冲刷工艺效果的有效手段。

3)建立水流作用下颗粒起动有效作用流速数学模型,提出了颗粒起动临界有效作用流速。研究表明,颗粒起动临界有效作用流速与颗粒起动临界流速、颗粒粒径和裂隙高度等因素直接相关。进一步地,颗粒表面的有效作用流速随裂隙高度的增大呈负相关的变化趋势。