以“造型数学”设计理念为主导的科技期刊版面构成形式研究

蔡顺兴 王慧娟

【摘要】为消弭国内科技期刊版面构成长期存在的设计弊端，文章应时提出改进思路，着力推动国内科技期刊与国际一流水准并肩看齐。欲实现此目标，一是需运用“造型数学”设计理念，精确设置版面构成网格比例，提高图文对位精度，力促版面布局统一规范，秩序井然。二是需通过计算、制式、秩序三维度，综合提升科技期刊版面构成质量。其中，计算是以数列运算为手段的网格构成原则；制式是以系统化、统一化、标准化为核心的网格营造样式；秩序则是体现网格构成数列级差韵律的审美保障，三者相辅相成，互为表里，使得科技期刊版面构成实用与审美兼具。

【关键词】“造型数学” 版面构成 计算 制式 秩序

【中图分类号】G230 【文献标识码】Ａ 【文章编号】1003-6687（2023）8-079-10

【DOI】10.13786/j.cnki.cn14-1066/g2.2023.8.012

出版史表明，任何种类的出版物，为赢得市场，无不明确出版方向，选择与之内容相协调的版面构成形式。如传统诗书文学类卷帙，多以谦和、儒雅的书卷气著称；时尚、艺术类期刊，向来以前卫、新潮的先锋性为长；而哲学、社科类读物，则以庄重、严谨见胜。[1]据此，以数理化内容为主体的理工类科技期刊，多把抽象、逻辑的设计形式作为版面构成取向，与科学出版内涵相统一，表里相符，以此彰显办刊特色。

一、国内科技期刊版面构成状况

科技期刊不仅担负着服务科技、提高社会生产力的传播任务，还承担交流科技信息、探讨前沿学术问题、普及科普知识等重任。[2]目前，国内科技期刊出版事业，处在平稳的发展阶段，然若要达到国际水平，实现与世界同步，必须全方位提高出版质量。仅就版面设计而言，仍存在着很大的提升空间。尽管国内科技期刊版面构成一向以条块分割简洁明了、图文布局清晰醒目立足于出版市场，然而在版面设计方面，与《自然》《科学》《新英格兰医学杂志》等世界一流科技期刊相比，仍存有明显差距。其因在于，中国科技期刊版面设计长期缺乏运用严谨、系统的“造型数学”网格构成方法精妙建构杂志版面实践，导致科技期刊理性、秩序审美品位不足。

“造型数学”设计思维对中国期刊出版业的影响，始于20世纪改革开放之初。彼时，以国内少数留欧精英为代表的归国专家，竭力将此设计观念和方法推广至设计界，并贯彻到教学实践中。如邱承德于20世纪80年代先后刊发了与“造型数学”设计方法相关的《开本、版心、插图与整体设计》《书籍版面与网格体系》等重要文章，对网格设计的目标、方法、手段等内容进行了详细阐释。同期，余秉楠系统地出版了《网格构成》《版面设计》《现代网格设计的科学性艺术性》等论著。由是，赋有“造型数学”内涵的网格构成理念开始在国内设计界出现，与书刊出版结伴同行，渐趋普及。

20世纪80年代中期，时任三联书店美术编辑室主任的宁成春，先后两次东渡日本求学。[3]1984年，宁成春被中国出版工作者协会委派赴日本讲谈社美术局研修一年。在日期间，其师从于受过德国乌尔姆造型大学理性主义设计教育的杉浦康平，移樽就教地向其请教网格构成。1986年，宁氏再赴日本，跟随横滨国立大学的真锅一男先生继续研修。[4]回国后，宁成春在“造型数学”设计理念的牵引下，运用网格构成法，不断尝试书籍整体设计，从封面到内页，从体例到结构，无不精心建构。《宜兴紫砂珍赏》设计（见图1），便是这一时期探索成果的体现。该作品“获得一九九二年香港印刷协会评出的编辑、设计制作、印刷等八项大奖，并荣获全场总冠军”。[3]继宁成春之后，国内也有少数专家获得了赴日本、欧洲研修网格设计的机会。如《书艺问道》（见图2）、《中央美术学院优秀毕业设计作品集》（见图3）、《汉字海报》（见图4）等，皆属研修者归国后完成的代表作。

尽管宁成春深谙“造型数学”网格构成之道，然而，国内如宁氏一般的实践者，仍屈指可数。由于当时出版界真正掌握这一设计方法的职业设计师人数有限，大部分从业者或从未接触过，或一知半解，皆缺乏足够的专业训练等，所以该设计方法与设计观念并未引起业界的足够重视。即使少数设计师掌握了这一方法，具体实施时，因工作繁杂辛劳，既费时耗神，又要求高，与快速高效的出版要求相悖，结果往往吃力不讨好，难被单位管理者理解和接受。不仅如此，部分从业者的工作积极性也不高。凡此种种，初期施行，成效并不显著。近年来，随着国内经济的快速发展，设计业取得了长足进步，以“造型数学”为主导的版面网格构成越来越受到人们的重视，但总体上仍逊于西方工业化国家。主要问题有以下几点。

1. 条块分割，精确不足

当前，国内科技期刊版面設计，普遍使用分栏法安排图文，粗看上去，并不觉得版面构成有何瑕疵，但若仔细审视，便会发现这类设计与运用“造型数学”方法求取网格分列精度的要求相比，存在一定的差距。诸如大小重叠网格之间的比例关系，分栏尺寸，图与图、图与文，正文与说明文，脚注间距，版心与页边距离等环节，并没有按照严格的数列倍率关系付诸精密计算，精准对位。甚至有些杂志“在边空留白时，时宽时窄，使人感觉太过拥挤或者太空”，[5]多显自由、即兴，整体性、统一性不足。对此，有专家指出：“长期以来，通过对国内杂志世界的观察，笔者发现一个很特别的现象，随便到书摊上买一本杂志，浏览一遍，大概都可看到不少具有创意的版式设计，但仔细观察之下，大多禁不住推敲。原因在于大家对栅格（网格）系统还缺乏足够的重视。”[6]无疑，此类构成形式仅为仿拟网格设计，与真正意义上需要运用“造型数学”运算之法，严格计算版面比例尺度之内涵无关。这一做法必会降低科技期刊的“造型数学”设计含量，有损严谨规范的秩序感、比例感，这也是国内科技期刊出版质量不及西方同类产品的重要原因之一。

需要说明的是，科技期刊版面实施不同层级的板块组合、栏目划分，并不等同于“造型数学”设计。大小有别的栏宽，固然由条块分割的方格组合构成，成为置入图文的基本架构，生成一种审美秩序，然而，并非所有网格组成的方格分栏，均具有“造型数学”的设计属性。只有那些经过严格的数列计算，相互间形成倍数关系，比例不等、设计创意独特的格子，才能体现出现代“造型数学”所赋予的网格构成内涵。

2. 套用模板，陈陈相因

据调查，“在数字时代，互联网上设计模板、设计素材等非常丰富，有的美编直接采用拿来主义，导致期刊版式设计雷同现象突出，缺乏创新”。[7]如此看来，国内期刊版式普遍套用电脑软件程序设计固定模板的做法，已成常态。然而，这一做法不仅让许多从业者失去了版式创新动力，还会使人误把概念化的模板条块罗列当成理所当然的合理化设计。如此版式构成缺乏欧美一流同类期刊设计所特有的新颖、丰富，及赏心悦目的审美品相，也就不难理解了。设计贵在创新，使用“造型数学”网格构成法设计科技期刊版面属于一种艺术创造活动，必须拒绝雷同，彻底摒弃缺乏差异性变化的电子网格模板。

事实上，网格设计十分珍视网格灵动组合带来的新颖变化，鼓励利用生动活泼、具有创造性的设计手段，追求多姿多彩、变化丰富的网格构成样式。采用“造型数学”设计方法，着眼于创新，为的是利用网格级数变化，获取赋有倍数律动的节奏感。这一设计方式本身并不会妨碍网格组合求新图变，其难点在于，既要使网格级数变化有序，整体连贯，又要避免布局单一、形式陈旧。套用固定模板的最大坏处，就是缺乏设计含量，否定了设计师的创造作用，成为敷衍了事、应付差事、流于形式的庸俗品。

3. 呆板乏味，随性轻率

目前市场上许多出版物版面的网格构成形式，明显存有两种弊端：其一，仅刻板地画格子填图文，缺乏创作激情，无意变更表现手法，寻找新的审美机遇；[8]其二，不愿在网格数列倍率计算方面下功夫，仅凭感觉随性位移，任意置放图文。这两种现象均是造成呆板、随性的主要原因。

“造型数学”网格构成，仅作为版面设计的辅助要素和设计手段，运用得合理，能够产生变化丰富、多姿多彩的视觉效果；反之，则会出现上述两种不良现象。囿于网格设计带有“羁绊艺术”的属性，[9]分割后的图文区域易受网格规矩约束，规矩本身含有标准、限制、呆板成分，但这并不是造成网格构成出现呆板、僵化的理由。恰恰相反，如若网格构成比例得当，制图规范，对位精准，可呈现出别具一格的机械美学审美魅力。

不可否认，网格规矩与限定、束缚相伴，强调借助大小不一的网格用于约束版面设计要素，使分割的版面依照网格倍率严格缩放，产生抑扬顿挫的节奏变化，以形成富有审美情趣的韵律感。网格设计一旦抛开了含有规矩、限定等因素的数学计算，必会丧失有规律的级差节奏变化。与规矩、限定相反的是，那种过于自由散漫，任意置放格子的做法，同样无涉网格设计本意，属于仿拟网格构成，抑或归为随性而动的自由版式设计之列，二者皆与科技期刊严谨的“造型数学”版面设计要求相悖。

正是由于网格构成具有规矩、限定特性，同时也存在呆板、僵化因素，这就需要针对局部网格进行必要的破网处理，以突破其规矩、限制的束缚，充分发挥网格的灵活性。同时还应当避免因网格过分灵活起不到应有的规矩、限制作用，而导致其功能丧失。显而易见，限制与灵活是一对矛盾，要想恰当确立二者的主从地位，妥善调和相互间的对立关系，需要具备深厚的艺术修养和敏锐的版面平衡眼光。同时需要恰当掌握“造型数学”网格构成之法，克服呆板、僵化的弊端，以及松散、放任等不足。如此，尚需设计师匠心独运，心智工巧地投入。

基于上述分析，要想推动国内科技期刊版面设计朝着高品质方向发展，须确立以“造型数学”为主导的网格设计方向，通过计算、制式、秩序三个维度，提升设计水平，消弭现有的缺陷，确保期刊版面构成实用与美感兼备，以彰显杂志办刊特色，筑牢市场生存根基。

二、计算——版面构成的数列运算维度

在以数列运算为手段的版面网格构成维度中，开本的确定便意味着运用数学计算求得版面网格级数比例程序的开启，接着，设计师按需将正文、注释、图形、符号等版面构成要素，纳入精心设置的网格结构中，意在获取良好的版面构成比例。这一设计方式，既是科技期刊基本功能的实际需要，也是现代理性主义设计精神的现实反映。在此，计算所依据的理性主义设计理论，主要涉及现代“造型数学”艺术观与西方传统数理认识两方面。

1. “造型数学”艺术观

“造型数学”一词，[10]源自荷兰“风格主义”运动的精神导师、通神论哲学家苏恩梅克尔，①其于1915—1916年先后出版了《世界的新形象》（The New Image of the World）和《造型数学原理》（Principles of Plastic Mathematics）两本书。苏恩梅克尔认为：“现实能够很好地表达一系列两极相反的力量——水平轴、垂直轴，以及各种原色之间的并置。”他还指出，“新的世界形象，就是要用一种可控的精确，一种对现实有意识渗透和精确的美去表现”。[11]

“‘造型数学从创造者的观点看，意味着真正的有条不紊的思想’……暗示如下的创作法则：我们现在研究着把我们想象中的现实转变成可以为理性所控制的结构，以便随后在‘一定的’自然现实之中重新发现这些相同的结构，从而凭借造型视觉去洞察自然。”[12] “风格派提倡数学精神，凡是缺乏明晰与秩序的表现，都被他们看作是‘巴洛克’的，统统予以反对。”这一理论的实质，即是把研究对象视为由“数”构成的比例世界，一切人化自然的和谐比例，均可凭借人的主观意志，通过级差倍数进行有序排列获得。在苏恩梅克尔看来，运用“造型数学”理论，“这种方法大约可以发展出一种大部分是建立在数学思维基础上的艺术来”，[13]（236）是放之四海皆准的真理。同为通神论信徒的蒙德里安十分赞同苏氏的观点，深刻地感悟道：“艺术如同数学，成为精确地表达宇宙基本特征的直觉手段”，并坚信“组成现实性結构的不是物体本身，而是它们之间的关系……所谓表达结构关系，便是用抽象的垂直线和水平线来组成简略的几何形体”。[12]

“造型数学”理念与期刊版面设计的结合，由《风格》（De Stijl）杂志创刊号设计引发，其中间过渡环节，是将“造型数学”理念转化为方格构成作品，再由方格形式精练为纵横交错的纯粹网格。蒙德里安作为先行实践者，运用等比数列方法分割矩形画面，把原色填入横竖交叉的黑色线框内，成功完成了大量极具抽象风格的画作。

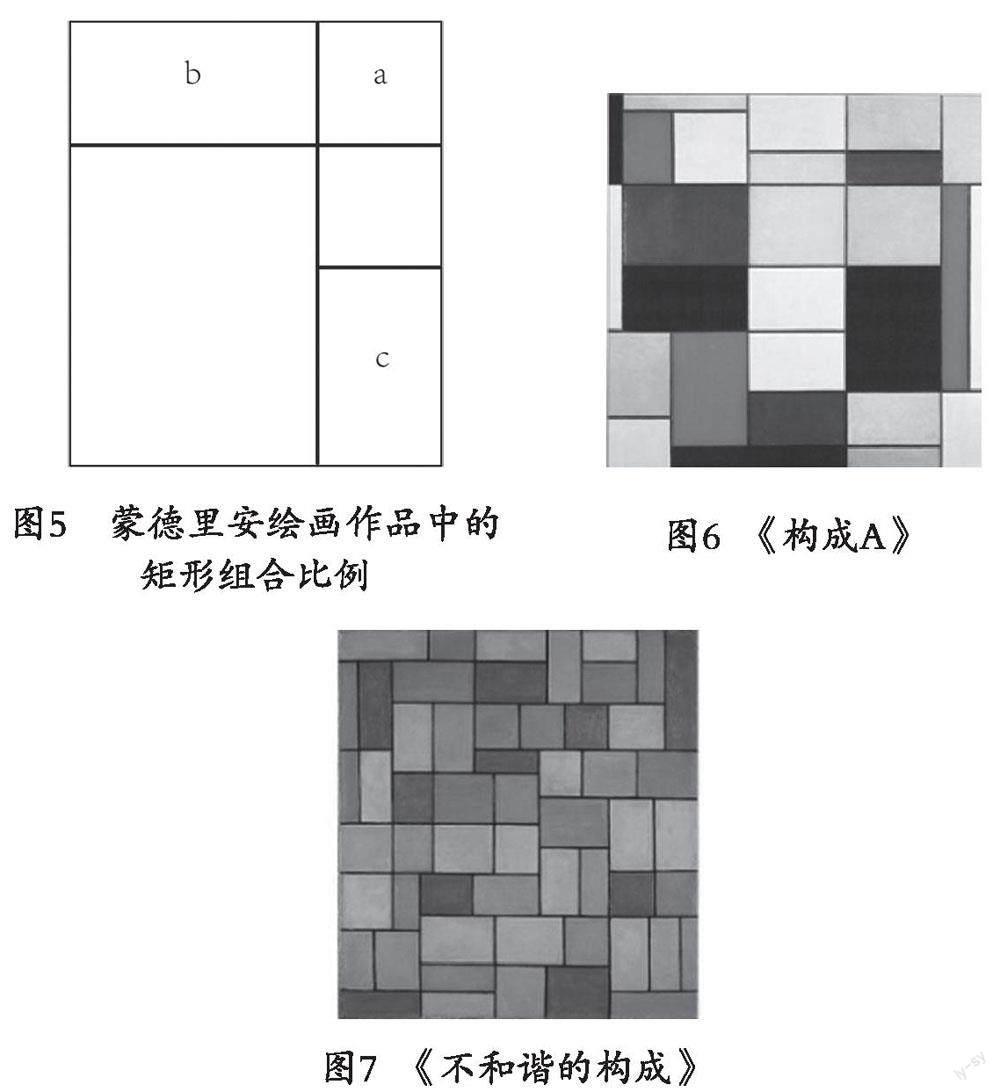
“在蒙德里安的绘画中常常能看到一些基本的形式，如图5中的a为正方形，b为双正方形，c为黄金长方形。”[14]案例中的矩形组合，选择几何级数递进方式，结合正方形求取黄金比，寻求不同矩形的比例变化。这一做法在蒙氏的画面构成中司空见惯，如《构成A》（见图6）。[15]不仅如此，彼时，一些受蒙德里安绘画的影响，持有相同艺术观念的艺术家，如范·杜斯伯格的《不和谐的构成》（见图7），循着同样的数学计算思路，创作了许多纵横黑色直线、拼合原色方块的抽象作品，与蒙德里安的画作形式相类，如出一人之手，理性程度达到了登峰造极的地步。[13]（183）

从这些大师现有的存世之作来看，“造型数学”艺术理念和以数列运算见长的现代网格构成体系，有着内在的紧密联系。如下页图8即是现代网格设计普遍采用的基本方法。图例“每一个网格单元由两种同等长度的平行线和垂直线组成几何级数的递进线。线与线之间的距离每次都增加一倍：X，2X，4X，8X，16X，依此类推”。[16]这一方法委实就是“造型数学”艺术理念应用的现实体现。科技期刊版面构成择此设计方法，与期刊的理性主义办刊内容、出版方向如出一辙。

2. 西方传统数理观

计算维度内所含有的“造型数学”审美内蕴，其本质与西方传统理性主义思想主张的数理观有着异曲同工之妙。学脉上，苏恩梅克尔的“造型数学”理论受新柏拉图学派的影响，此学派属于毕达哥拉斯思想体系范畴，蒙德里安的新造型主义艺术观正来源于此。

历史上，欧洲从公元前六世纪开始，审美的比例标准就已形成。当时“‘数’对毕达哥拉斯学派来说，是一个基本的观念”，他们认为“数为自然中最首要（第一位）的东西”，[17]因此，“数”作为万物之始基，与比例的关系十分密切，“没有一门艺术的产生不与比例有关，而比例正存在于数之中，所有一切艺术都产生于‘数’”。[18]执持这一观念的柏拉图同样认为，“数是一切美好的事物的源泉，它代表着秩序和谐，而一切无序混乱、无节奏、不和谐以及一切与恶相关的东西，都是因为数的缺乏”。[19]如古希腊城邦规划、神殿建造使用的黄金比例，即是毕氏理论的代表。经现代人测量，帕特农神殿的台基至山墙顶端的比例为1：1.618（见图9），千百年来，这一数值始终被人类社会公认为最合理、最美观的数学比例之一。[20]

文艺复兴以后，西方社会把数学计算应用于印刷出版领域几近常态。如《人体比例四书》的作者阿尔布雷希特·丢勒，于1525年出版的《艺术课上的尺规测量法》文集中，收录了一篇名为《论字母的正确造型》的文章，具体讲述了如何为字母构造提供正确的网格计算方法，即是典型的例证。这表明，当时的许多艺术家、建筑师将字母安排在网格内（见图10），以不同比例的圆形、矩形表现罗马字母细节，努力塑造字形之美。[21]

事实证明，自古典时代起，直到近现代“造型数学”理论的出现，西方审美认识从未离开过数学计算。有必要说明的是，古典时期人类运用数学对于客观对象审美规律的探索，强调的是形体结构之间形成的数理逻辑关系，而对于宇宙基本特征（本质结构）的认识，并没有给出明确的答案，故而，有别于新柏拉图学派理论，对于“造型数学”以一种“积极的神秘主义”，[22]将纵横直线交叉结构作为对宇宙基本特征认识的看法。[23]

由此来看，把握版面构成的数学计算维度，不仅是“造型数学”艺术主张的客观体现，也是西方传统理性主义之光投射在科技期刊设计上的反映。借助数列运算，极易得出和谐、恰当的网格比例，正如爱因斯坦所言：“正是由于这么一个比例尺度，它使人做好容易而做坏难。”[24]对于以传播科学知识见长的科技期刊来说，运用“造型数学”设计方法，既可合情合理地体现理性之美，又十分契合期刊的办刊目标。

三、制式——版面构成的统一标准维度

制式，即是将“造型数学”的具体表现方法施用于科技期刊版面构造，使横竖直线交叉产生的网格成为版面构成的组织要素，结合一定的骨架结构，形成系统化、统一化、标准化的网格营造样式。网格系统由矩形方格发展而来，本身并没有特殊的个性，只是版面构成普遍使用的基本元素而已，不过其可拼合组成千变万化的网格构成形式，一旦这一形式发展成为组织严密的设计系统，有了规范、标准的实用价值，制式化网格便得以形成。

制式化网格设计十分讲究利用比例原则，高妙分割版面，突出版面级差次序，注重使用纯粹理性的简约方法，把图文的排列位置，依照比例、力场、方向、节奏等形式法则规律合理规划，以达到和谐条理、赏心悦目的设计目标。如排版上一律使用简约、规整的纵横结构，选择无饰线体作为主要字体，“得到的平面效果非常公式化、标准化和规范化，因此自然具有简明而准确的视觉特点”。[13]（234）这一高度理性化、系统化的设计方式，不仅是现代主义设计的重要理论基础，同时也是出版界科技期刊的重点选择。

1. 现代制式化网格设计之始发

毋庸置疑，网格使用，古已有之，却有别于现代体系化、制式化的网格设计系统。现代网格设计的产生、发展，乃至波澜壮阔的制式化网格设计艺术潮流的涌现，一是发端于范·杜斯伯格亲手创办、维尔模斯·胡札设计的《风格》期刊（见图11）；二是与模数设计理论密不可分。

与蒙德里安一样，同为苏恩梅克尔哲学思想的拥趸，范·杜斯伯格始终高举“造型数学”理性主义大旗，不遗余力地推广传播风格主义艺术理念，最终使得这一设计主张全面朝着抽象、理性、纵横直线交叉结构方向发展，为制式化网格设计体系的诞生奠定了基础。

（1）风格派对于网格设计的探索。制式化网格最初的先行探索者，多为受“造型数学”精神驅动的风格派成员，之后，通过所有参与者的不断实践和努力，持之以恒地坚持纵横直线交叉构成理念，大大拓宽了“造型数学”设计的影响力。然而，真正将直角网格转化为成熟的设计体系，主要由秉持风格主义精神的包豪斯一派以及瑞士巴塞尔高等美术学校的师生共同完成。换言之，至20世纪50年代，沉浸在“造型数学”氛围中的瑞士网格设计探索，经不断发展，逐渐形成制式化的设计体系，慢慢波及全球，发展成声势浩大的国际主义设计潮流，“国际主义设计”一词也因之而起。[25]

（2）模数理论对于网格设计的贡献。制式化网格设计体系走向成熟，是多重复杂的社会文化和设计力量合力促成的结果，其中，模数设计理论尤为突出。模数理论，即“勒氏模数”，由法籍瑞士建筑设计师勒·柯布什耶创立。此设计理论的核心内容，与“造型数学”艺术主张存在着类似之处，二者皆强调运用数列方法，按比例分割矩形版面。模数设计凭借数学计算，把单体矩形作为模数构成基本单元，依据数列分列原则，对单元方格按比例进行网格分割。

柯布什耶的模数理论来源，重点以古希腊太阳神雕像黄金比的测量数值为依据，用尺度分析法，“实现了数学秩序和人体比例尺度的对应”。[26]在此基础上，勒氏先把一个矩形方格作为标准单元，按需复制44个（见图12），后逐一对每个单元矩形版面按比例施以纵横直线划分，最后将所有单元整体组合在一起，便形成了统一、标准的制式化网格。马赛公寓即是勒氏根据该制式化网格设计方案实施的成功典范，此作品的诞生具有划时代意义，不仅在建筑领域影响甚大，也为期刊使用制式化、标准化的网格设计手段，提供了理性表现的新思路。

2.完善的制式化网格设计系统

制式化网格设计系统，常用的普遍类型有：单一矩形网格设计系统、混合矩形网格设计系统、纵向竖排网格设计系统等。此类网格系统不仅适用于科技期刊版面建构，同样也适用于其他类别的书刊设计，只不过相较于其他出版物，理性、抽象、制式化的网格构成形式，更符合科技期刊的内容需要和杂志形象展现。

（1）单一矩形网格设计系统。科技期刊采用制式化单一网格设计的关键在于，一是先用水平垂直交错直线构成网格，满版铺陈后，再以独立网格作为基本模数单位，与底层网格形成倍数关系，通过单元组合，将矩形方格合并为功能不等的二栏至三栏，如美国的《科学》杂志版式设计（见下页图13）。版面上正文采用的双栏结构，简单明了，与通栏主标题一致，均由较小的矩形网格合并而来，以便直观、高效地传达纯文本信息。

（2） 混合矩形网格设计系统。许多情况下，科技期刊的版面编排，除正文外，还须配合文中内容，安排大量的图表、图像、符号、注释等要素。在此前提下，运用单一矩形网格不足以解决布局困难，故而应根据实际需要，将版面设计成大小矩形混编的网格系统，通过一层、二层、三层，甚至四层网格，形成条理清晰、井然有序的图文布局，便于读者阅读。如《生物科学》内页版面设计（见图14），左页整体结构由矩形网格合并成一大栏、二小栏；右页在二小栏的基础上，再细分为更小的四栏，为的是繁而不乱地安排成分不同的插图、符号、数据、注解等内容。尽管图文复杂、构成繁复，但因梳理清晰、层级有序，读来使人明了易懂。此类混合矩形网格系统，经长期演进，已逐渐发展成制式化设计形式，成为科技期刊常用的版式结构。

（3）纵向竖排网格设计系统。随着西方现代“造型数学”网格构成的普及，至20世纪50年代，此方法渐渐演变成国际主义设计潮流，虽然20世纪70年代曾一度式微，但很快又活力焕发，直至当下。[13]（234）现代网格设计，为适应竖版文字编排的需要，日韩等国及我国港台地区的科技期刊版式，大量采用直列竖排网格样式，尤其是与汉字同属表形文字的日文期刊，更加重视对直列竖排网格构成方法的研究，通过深入探索，结合“造型数学”原理，汲取中国古籍传统竖排精华，创造出能够满足现代表形文字编排需要，符合制式化纵向竖排网格构成标準的设计系统。如日本《真知》杂志版式构成（见图15），[27]由杉浦康平亲自设计，其正文、注释排版，均采用直列竖排网格与插图栏横排文字相配合，呈现出直列竖排为主，水平横排为辅，主次分明，重点突出的布局样式。

简言之，上述三种制式化网格设计系统，仅为常用的主流式样，现实中远不限于此。实际上每一种独具审美创意，符合统一化、标准化设计要求的网格构成系统，均赋有制式化网格设计之属性，将其巧妙应用于科技期刊版面设计，不仅是理性主义设计精神的物化体现，也是科技期刊图文内容与设计形式高度统一的反映。

四、秩序——版面构成的审美欣赏维度

在秩序维度中，“美作为有意味的形式”，[28]深藏于网格级数变化的节奏律动中，仔细品味才能有所感悟。版面构成对于秩序的追求，不仅是为解决条理清晰的信息传达问题，还包括建构节奏明快、版面和谐的形式美。一方面，布局谨严、章法规范、穿插有序的网格系统，可通过秩序彰显隐藏在网格构成背后的“有意味的”级差韵律美；另一方面，能够使版面图文布局具有思路清晰、层次分明的使用价值。正如鲁道夫·阿恩海姆所指出的那样：“人所具备的认识能力（其中也包括艺术创造能力）寻求的是秩序。科学的使命是在多样化的现象中提炼出有规则的秩序，而艺术的使命则是运用形象去显示这种多样化的现象中所存在的秩序。”[29]无疑，艺术运用形象去显示秩序指的就是形式美，也是版面构成谋求的重要核心要素之一。

蕴含“造型数学”理性内涵的科技期刊版面设计，图文排列整齐划一，归因于秩序使然。有序的版面构成能够引导读者沉醉于文本阅读的享受中，陶冶性情。确切地说，版面上大小不等的网格，条块分割、疏密有致、层次丰富，形成有节奏的美妙变化，读者玩味，可从中获得悦目娱心的美感满足。显然，有条不紊的网格营造是秩序形成的必要条件，而韵致迷人的秩序则是网格构成形式始终不变的向往，故而，秩序美感存在与否，取决于大小网格之间是否分列着恰当的级差比例。

1. 级差比例形成秩序美

科技期刊版面设计运用“造型数学”的主要目的之一，就是通过有规律的网格级差变化获得秩序美，《风格》杂志第一期的封面版式设计即为这一苦心构思的体现。其表现手法以开拓性的艺术创意，有序组合面积不等的黑色矩形，把参差错落、疏密有度的长方形图式设计成正负构形精妙、黑白分布平衡的逻辑整体，以造型独特、抽象理性的视觉符号享誉世界，充分体现出风格主义秩序之美的创作理念。《风格》杂志版式构成，之所以看上去理性、秩序，是比例不等的矩形条块采用数列等比分割，井然布局的结果。对此，有兴趣的数学家对这一现象进行了科学探索，试图使用数列方法找出风格主义版式设计秩序之规律。

数学家曾将蒙德里安画作中存在的数学现象作为有趣的数学难题展开深入研究，[30]专门对尺寸为n×n的正方形网格进行划分，由此发现了秩序美的形成规律。具体为：在n×n的正方形内（见图16），运用网格划分方法，将正方形版面分割为数量不等，形态、面积均不相同的长方形与正方形，把最大和最小的矩形面积相减后所得出的数值，就是长方形和正方形的最佳组合比例。即是说产生的这个比例，无论长方形和正方形如何自由组合，组合后的版面形态皆能形成具有最佳级数比例的秩序美。图16中的10×10方格解决方案，得分为8，即是最优值，产生的网格级差比例为：12、14、16、18、20，体现出秩序之美。

2. 体验欣赏秩序之美

科技期刊版面构成对于秩序的追求，主要是为通过有规律的网格数列级数变化获得赏心悦目的韵律感，阅者尽心体会，可从中领略秩序之美的形式魅力。

（1）网格促成秩序美。运用“造型数学”设计理念精心构建的网格，大体分为简单、复合、重点三类，通过分割、排列、重叠组织要素，以收获和谐的版式结构。如简单网格结构单一、纯粹，主次分栏明确，简约精练。复合网格结构着力解决科技期刊繁复、纷乱、种类驳杂的内容安排，使主体正文、注释参考、图表符号、插画说明等要素，纳入标准规范的大小栏目中，生成条块鲜明、层次清晰、秩序井然的版面系统。而重点网格则表现为同一版面不同网格间的多层组合，必须遵循主次分明的原则，依照版面内容的先后顺序，重点突出，如此，秩序之美随之而生。

（2）线性欣赏秩序美。数字时代，纸媒体式微，读者阅览纸质杂志追寻的是重温过往温暖的读书回声，阅读欣赏尤显珍贵，赏阅方式与线性秩序编排共生并存。换言之，按内容先后顺序线性排列图文，是所有类别纸质媒体的共性，科技期刊概莫能外。读者依照排版次序，审视起伏律动的图片、图表、符号，品读参差交错的正文、注解、图释，聚精会神地线性欣赏繁而不乱的要素排列形成的秩序之美。美文佳作，力透纸背，按序阅读，能为读者带来怡情养性的快乐，快乐即是美，故而，真实现实的在场，依序线性阅览，力求主线明确，始终是纸质科技期刊静态图文不变的属性，表明线性阅读离不开秩序，秩序引发美感。

（3）悉心体验秩序美。版面能否产生独出机杼的秩序之美，归根结底取决于阅读者对于网格构成美感的真切体验。就现代国际著名的科技期刊版面构成来说，别具匠心的艺术创意，其条理、秩序的表现形式，或以简约、凝练的符号呈现，或以混沌、繁复的图式出场，抑或二者同时展示。无论属于哪一种类型，都需要阅读者细细品味，才能体会到版面秩序之美的绝妙。

综上，秩序之美不仅仅是将版面构成要素共置于统一的网格框架内，以获得条理清晰、便于阅读的版式功能，还包括将“复杂的排版变得方便简洁”，[31]使无序混乱的图文要素，在协调共生中呈现出超越知识信息的视觉美感。

结语

出版市场竞争激烈，任何种类的期刊若想站稳市场，必须明确自身的办刊特色，其中包括择取与办刊方向一致的版面设计形式。科技期刊素来把理性、抽象的设计表达作为版面的构成取向，竭力满足办刊所需，以赢得市场。当前，国内科技期刊出版事业正处在欣欣向荣的稳定发展中，现有的杂志版面设计多以图文编排明晰达意，栏目布局理性简约蜚声出版界，然而，若与世界一流科技期刊设计水准相较，多有不及。要想缩小差距，力争赶超，国内科技期刊须以“造型数学”设计理念为主导，着力实施理性主义网格构成。

运用水平垂直交叉直线建构期刊版面，始自倡导“造型数学”理念的《风格》杂志设计，这一方法具有普适价值，尤其适用于那些重视抽象思维、演绎推导、数据分析类别的学术刊物。为此，以逻辑、理性著称的科技期刊，运用“造型数学”网格设计方法营造版面，不仅与杂志本身的办刊理念十分吻合，同时也与期刊所承担的科技信息传播使命协调一致。其版面构成主要涵盖计算、制式、秩序等三维度。

首先，计算是科技期刊版面网格构成的基本维度。其既是构建版面网格比例的具体运算方法，也是现代“造型数学”数列内涵的实际体现。其次，制式是统一化、标准化的科技期刊版面网格营造维度。在此维度中，要求别具意匠地使用系统规范、整体统一的网格构成形式，强调设计表现必须简约抽象、有序条理。最后，秩序是科技期刊版面网格构成的审美维度。在秩序的维度里，“美作为有意味的形式”，隐含在网格布局的级差比例中。受倍率不等，井然排列的网格控制，大小不同的版面图文可产生富有节奏感的级差秩序美。现实实践中，三类维度互相依存、相得益彰，力促版面网格构成实用与审美兼具。

參考文献：

[1] 张莉. 浅谈杂志版式设计[J]. 编辑学刊，1999（5）：48-49.

[2] 郝秀原. 论科技期刊的社会责任[J]. 中国科技期刊研究，2013（4）：628-630.

[3] 汪家明. 设计有道——宁成春的书籍设计[J]. 读书，2022（7）：168-175.

[4] 深圳书籍设计论坛[EB/OL].[2023-04-20].http：//www.333cn.com/graphic/hyzx/127023_3.html.

[5] 周琼. 期刊版面设计中存在的问题及对策[J]. 美术教育研究，2012（9）：101.

[6] 严汉钦. 杂志版式设计中的栅格设计[J]. 视听，2012（7）：73-75.

[7] 潘越. 期刊版式设计的时代演变意义及工作思路[J]. 传播与版权，2022（12）：35-37.

[8] 李雪枫. 学术期刊版式设计现状的调查分析[J]. 编辑之友，2007（6）：74-75.

[9] 林文霞. 雷圭元谈图案美学[J]. 新美术，1986（3）：55-57.

[10] Art Movements in Art History-Mondrian and De Stijl， Drawn from Notes Compiled by R. Becker for the University of South Africa[EB/OL].[2022-12-02].https：//www.the-art-world.com/history/de-stijl3.htm.

[11] De Stijl， New Media， and the Lessons of Geometry by Jessica Helfand[EB/OL].[2023-01-12].https：//www.typotheque.com/articles/de_stijl_new_media_and_the_lessons_of_geometry.

[12] 邵大箴. 论抽象派艺术[J]. 文艺研究，1988（1）：126-143.

[13] 王受之. 世界现代平面设计史[M]. 北京：新世纪出版社，1998.

[14] 余璐. 余秉楠——世界设计大师丛书[M]. 郑州：河南美术出版社，2004： 254-255.

[15] Mondrian & His Later Years， Posted by Matt Knight. Masterpieces of Art[EB/OL].[2023-01-12].http：//blog.flametreepublishing.com/art-of-fine-gifts/bid/77772/Mondrain-His-Later-Years-Masterpieces-of-Art.

[16] 余秉楠. 网格构成[M]. 天津：天津人民美术出版社，1986：20.

[17] 叶秀山. 毕达哥拉斯学派和希腊科学精神[J].社会科学战线，1993（2）：106-114.

[18] 闫伟. 理性与非理性——古代文明影响下的毕达哥拉斯美学思想[J]. 文学界（理论版），2012（12）：253-255.

[19] 毕祖曜. 柏拉图对话中的德性和数学知识[J]. 西南交通大学学报（社会科学版），2020（2）：136-143.

[20] Geometria ed Arte： il quadrate[EB/OL].[2022-12-15].http：//www.didatticarte.it/Blog.

[21] 扬·米登多普. 文本造型[M]. 杨慧丹，等，译. 北京：中信出版集团，2017：42.

[22] 中国科学院物理所. 方格中藏匿的数学与哲学[EB/OL].[2022-12-12]. https：//www.sohu.com/a/478730766_119097.

[23] Summary of De Stijl[EB/OL].[2023-01-20].https：//www.theartstory.org/movement/de-stijl.

[24] Richard Hollis. Graphic Design——A Concise History[M]. London： Thames Hudson Ltd， 1994： 130.

[25] 余秉楠. 现代网格设计的科学性艺术性（上）[J]. 中国出版，1993（8）：40-43.

[26] 唐露嘉. 理性·秩序·比例 ——勒·柯布西耶的模度理论与应用探究[J]. 建筑技艺，2022（S1）：217-221.

[27] 杉浦康平. 疾风迅雷——杉浦康平杂志设计的半个世纪[M]. 杨晶，李建华，译. 北京：生活·读书·新知三联书店，2006：61.

[28] 李泽厚. 美的历程[M]. 北京：中国社会科学出版社，1984：22.

[29] 鲁道夫·阿恩海姆. 艺术与视知觉[M]. 滕守尧，朱疆源，译. 北京：中国社会科学出版社，1984：196.

[30] The （Mathematical） Problem of Mondrian's Paintings， Logic， Mathematics[EB/OL].[2023-02-01].https：//www.bbvaopenmind.com/en/science/mathematics/the-mathematical-problem-of-mondrians-paintings.

[31] 王璐. 版面编排的网格形式[J]. 编辑之友，2015（4）：90-93.

① 作为一位数学家和通神论者，苏恩梅克尔奠定了“风格主义”运动的哲学基础，规划制定了“造型数学”的艺术原则。

The Layout Composition of Scientific and Technical Journals Dominated by the Design Concept of  "Plastic Mathematics"

CAI Shun-xing， WANG Hui-juan（School of Art， Southeast University， Nanjing 210096， China）

Abstract： In order to eliminate the long-standing design shortcomings in the layout composition of domestic scientific and technological journals， this paper timely proposes ideas for improvement， and vigorously promotes domestic scientific and technological journals to be on par with international top-class standards. In order to attain this goal， firstly， we need to use the design concept of "plastic mathematics" to accurately set the grid proportion of layout composition， improve the accuracy of the alignment of graphics and text， and promote the uniformity， standardization and orderliness of layout. Secondly， we must improve the quality of layout composition of scientific and technological journals through three dimensions， including calculation， format and order. Among them， calculation is the principle of grid composition by means of series operation; format is the style of grid creation centered on systematization， unification and standardization; order is the aesthetic guarantee embodying the differential rhythm of grid composition sequence. Mutually complementary and supportive， the three dimensions make the layout composition of scientific and technological journals both practical and aesthetic.

Keywords： "plastic mathematics"; layout composition; calculation; standard format; order

基金項目：国家社会科学基金艺术学项目“中国现代平面设计艺术观念史”（17BG126）

作者信息：蔡顺兴（1962— ），男，江苏南京人，博士，东南大学艺术学院教授、博士生导师，主要研究方向：设计学、艺术学理论；王慧娟（1982— ），女，山东潍坊人，东南大学艺术学院博士研究生，主要研究方向：设计学、艺术学理论。