无磁轭轴向磁通风力发电机多目标偏好优化设计
曹永娟, 顾迪, 冯亮亮, 张伟, 李康, 毛瑞 ,2
(1.南京信息工程大学 自动化学院,江苏 南京 210044; 2.江苏省大气环境与装备技术协同中心,江苏 南京 210044)
0 引 言
轴向磁通永磁电机(axial flux permanent magnet machine,AFPM),也称盘式永磁电机,具有轴向尺寸短、效率高和功率密度大等特点[1-2],适用于风力发电、航空航天及电动汽车等领域[3]。文献[4]对比分析了2种不同永磁结构AFPM的气隙磁密和电压谐波含量,发现采用Halbach永磁阵列的发电机电压波形正弦性更好,但其转子背铁为金属材料,成本高,转动惯量大,启动困难。文献[5]提出一种PCB(printed circuit board)盘式发电机的不等宽分布式绕组,降低了铜耗,但定子无铁心导致气隙较大,电机的效率和功率密度不高。文献[5]设计了一种电动汽车用分块铁心AFPM,定子无磁轭,降低了电机的损耗和重量,电机具有较高的效率和功率密度。文献[7-8]将3D打印技术应用于电机设计,利用其自由度高、无需模具、材料利用率高、生产周期短的优点设计磁阻电机转子,减少了漏磁,提高了电机的制造效率。
为了高效设计输出性能优异的发电机,将电机设计与多目标偏好优化(multi-objective preference optimization,MOPO)相结合。文献[9]采用响应面法优化分析了单边盘式发电机的磁钢厚度与形状,降低了波形畸变率(total harmonic distortion,THD),提高了电机的效率,但优化目标仅是二维。文献[10]采用响应面法和改进粒子群算法优化设计了无轴承永磁同步电机的转矩和悬浮性能,建立了二阶响应面法(response surface method,RSM)模型,但没有对比评估其与高阶RSM的拟合效果,优化目标之间无偏好差异。文献[11-12]结合了响应面法与多目标遗传算法对电机进行优化设计,前者没有体现出目标偏好,后者虽然在磁能利用因子中给出了权重系数,但没有针对全局优化目标做偏好优化。文献[13]优化设计了磁极径向组合AFPM,采用加权优化目标组合获得了偏好平均转矩的优选方案,但没有对比分析不同偏好与无偏好的优化方案。文献[14]为了得到一种较好的变压器参数优化设计方法,对遗传算法(genetic algorithm,GA)、差异进化算法(differential evolution algorithm,DEA)、多目标遗传优化算法(non-dominated sorting genetic algorithm II,NSGA-II)进行比较,结果表明NSGA-II提供了更好的方案。文献[15]采用NSGA-II对无轴承永磁同步磁阻电机的转子拓扑结构优化设计,并做了样机实验,验证了NSGA-II的有效性。文献[16]采用改进的遗传算法NSGA-II-M对轴向磁场永磁记忆电机优化设计,结果表明NSGA-II-M在求解带约束条件的多目标优化问题上具有较好的优势。
结合混合Halbach永磁阵列的优点以及3D打印的技术特点,本文提出一种无磁轭模块化轴向磁通风力发电机(yokeless segmented axial-flux wind generator,YSAFWG),一方面推导了尺寸设计公式,提出了初始设计方案,另一方面,基于电机的功率尺寸方程选取优化变量,确定偏好优化目标,对参数进行灵敏度分析,采用响应面法和经改进的NSGA-II对电机进行多目标偏好优化设计,评估二阶和高阶RSM的拟合模型,最后,对比2种方法的偏好THD优化结果,确定电机的结构参数,并通过样机实验验证电机性能。
1 YSAFWG拓扑结构与设计要求
本文设计的YSAFWG采用双外转子、中间单定子的对称结构,电机受力均衡,其基本结构如图1所示,包括模块化定子铁心、双侧对称磁钢盘,以及温度使用范围宽、高机械强度赛钢塑料(polyformaldehyde,POM)材料所构成的定转子支架和机壳。定子采用分数槽集中绕组,模块化铁心由带状硅钢沿径向正反叠压而成,增大了机械应力,由定子支架固定在机壳上。转子磁钢盘由N-S极相对的2个混合Halbach永磁阵列构成,无需转子磁轭,可以增大气隙磁密幅值,改善波形正弦性,永磁体表贴在两侧转子支架的内嵌环中,提高了运行稳定性。

图1 YSAFWG的基本结构Fig.1 Topology of YSAFWG
图2为电机的等效磁路图,其中:Fm为永磁体磁动势;Rm为永磁体磁阻;Rσ为永磁体漏磁;Rδ为气隙磁阻;Rt为定子齿磁动势;Fa为定子绕组磁动势;定、转子轭部磁阻均为0,减少了铁耗,简化了电机磁路结构。

图2 电机等效磁路图Fig.2 Equivalent magnetic circuit of YSAFWG
无磁轭模块化轴向磁通风力发电机可用于小型风光互补路灯、家用电器等场合,综合考虑电机的性能以及空间安装尺寸,确定了如表1所示的电机设计要求。

表1 YSAFWG的设计要求Table 1 Design requirements of YSAFWG
2 YSAFWG轻质节约设计
2.1 电磁特性
YSAFWG定子无磁轭,主磁通沿两侧永磁阵列闭合,电机效率高,根据文献[17],其电磁功率可表示为
Pem=mKpErmsIrms。
(1)
式中:m为电枢绕组相数;Erms为相感应电动势有效值;Irms为相电流有效值;Kp为电磁功率波形系数。
相感应电动势有效值表达式为
(2)
式中:Ke为感应电动势波形系数;N为每相串联匝数;Bav为气隙磁通密度平均值;Sa为每极磁通的有效面积;p为极对数;n为电机的额定转速。
每极磁通有效面积为
(3)
式中:αs为单个模块化定子铁心气隙侧面积与一个齿距内定子面积的比值;z为模块化定子铁心个数;Di为定子内径。
单相平均电负荷为:
(4)
(5)
式中:a为电枢绕组并联支路数;Dav为定子的平均直径。
将Erms、Irms代入式(1),定义λ=Do/Di,为定子外径与内径之比,化简可得
(6)
(7)
2.2 初始结构设计
YSAFWG为小型风力发电机,额定功率PN=30 W,额定转速n=600 r/min,由文献[1]可知,一般AFPM的定子直径比在1.5~2.2之间,本文选取λ=1.85。为了充分利用风能,极槽配合选取14极12槽的多极结构;极弧系数小可以减少漏磁,但极弧系数过小会引起每极磁通量降低,导致绕组匝数增加、气隙增大,一般选取极弧系数为0.8左右。YSAFWG为双气隙结构,气隙越小,气隙磁密越大,但受加工工艺的约束,气隙不易过小,本文初选单边气隙长度为0.8 mm。考虑定转子支架的机械支撑作用,转子支架厚度取为磁钢厚度的两倍,定子支架厚度近似为定子轴向长度,保证电机的稳定运行。基于以上分析,采用与传统轴向磁通电机相似的设计方法[17],得到如表2所示的YSAFWG初始结构尺寸参数。
2.3 主要材料分析
2.3.1 磁钢选择
为了提高工作磁通,轴向充磁磁钢材料选择高磁能积的钕铁硼N35,而周向充磁磁钢并不是磁路主要磁势源,为作最适选择,周向充磁磁钢材料Mcpm初步选择铝镍钴9、钕铁硼N25、钕铁硼N35三种常用永磁材料,利用有限元仿真得出YSAFWG采用不同材料时的平均气隙磁密Bav、相感应电动势幅值(electromotive force,EMF),结果如图3所示。当Mcpm采用AlNiCo9材料时,Bav、EMF相对较小,采用钕铁硼N25的结果与N35相接近,而N25的成本较N35低了超三分之一,因此,本文Mcpm选用钕铁硼N25。
2.3.2 不同材料的重量比较
电机一般采用金属材料,本文采用3D打印POM技术,POM材料机械强度高,满足小型发电机应用要求。图4为电机不同结构采用3D打印POM与金属材料的重量对比,单位为千克。可以看出,3种结构采用POM的重量远小于金属材料。YSAFWG初始参数采用金属材料的重量为3.34 kg,远超电机的设计要求,而采用POM材料的方案与其相比,重量减少了56.89%,满足设计要求,降低了电机的转动惯量。
2.4 多目标偏好优化设计
由式(6)可知,YSAFWG电磁功率受电磁功率波形系数、感应电动势波形系数、电机外径、气隙磁密平均值、永磁体极对数、每相串联匝数、模块化定子铁心气隙侧面积等因素影响。电机的初始设计方案并不能使其性能达到一个相对最优值,为了具有更好的输出性能,选取极弧系数、单边气隙长度、定子槽宽为优化变量,相感应电动势幅值、相感应电动势的总谐波畸变率、齿槽转矩峰峰值为优化目标。考虑到风力发电应用场合,本文以表征发电质量的THD为主要偏好目标,EMF和Tcog为次要偏好目标,此外,加入目标约束,保证优化后电机的性能符合设计要求。
YSAFWG采用了Halbach阵列,αp的取值既要为周向磁钢留有余量,也要考虑到工作磁通;hap过大会影响电机性能,过小则使电机装配困难,工艺上也难以实现;ws过大会使铁心过饱和,过小则难以放置绕组;综上考虑,优化变量及其3个水平的取值如表3所示。

表3 优化变量及其3个水平的取值Table 3 Optimization variables and values at three levels
本文采用响应面法和改进后的NSGA-II对YSAFWG进行偏好THD优化,为了提高优化的精确度,评估了二阶和高阶响应面拟合模型,并对比2种优化方法,优化流程如图5所示。各个因素在不同阶段对同一个目标的灵敏度方向可能不同,将优化因子对目标的灵敏度分为-1~0、0~1两个水平阶段,参数灵敏度分析如图6所示,优化目标之间相互制约,例如,极弧系数在-1~0阶段,随着极弧系数的增大,EMF增大,THD和Tcog减小,而在0~1阶段,EMF和Tcog减小,THD却增大,体现优化参数选取的正确性。为了表征不同目标之间的偏好差异,加入偏好函数,多目标偏好优化数学模型为:
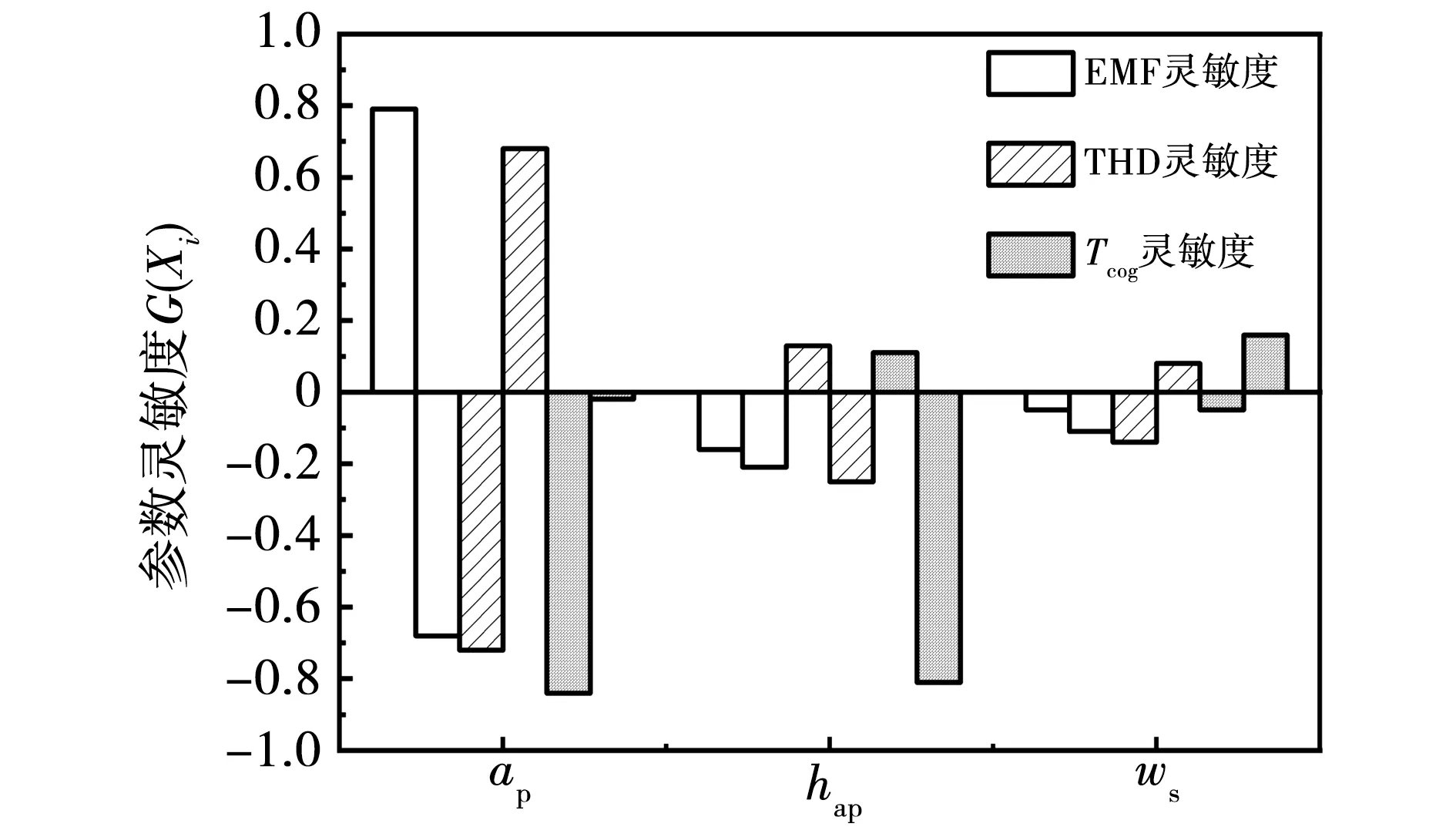
图6 参数敏感度分析Fig.6 Parameter sensitivity analysis
(8)
式中:fn(Xi)为优化函数;ft(Xi)为偏好函数;Xi为优化变量;k1、k2、k3分别为3个优化目标的偏好系数,k1+k2+k3=1,考虑到各个目标对电机性能的影响,取主要偏好目标的系数为0.7,次要偏好目标系数均为0.15。
3 带目标偏好的RSM优化设计
3.1 RSM多目标实验设计
一般在电机优化方面采用多项式RSM模型,三阶RSM数学模型如下式,去除三次项后即为二阶RSM模型:
(9)
式中:ε表示拟合误差常量;β为回归系数。
最常用的RSM主要包括中心复合设计(central composite experiment design,CCD)和BBD设计(box-Behnken design)[18]。本文为三因素三水平设计,若采用CCD设计一般需要20次实验,而采用具有旋转性的BBD设计只需要15次实验。为了保证模型拟合精度,减少实验成本,本文选取BBD设计方法,实验安排与数据结果如表4所示。

表4 BBD试验设计表及其仿真结果Table 4 BBD design table and simulation results
3.2 RSM模型评估
分别对2个模型进行修改,抑制P值大于0.05和信噪比小于4 dB的不显著项后,模型对比评估结果如表5所示,高阶RSM模型的P值、信噪比明显优于二阶模型,并且高阶模型的失拟项均为不显著,而二阶模型的THD与Tcog的失拟项显著,高阶RSM模型较二阶表现出更高的可信度,下面采用高阶RSM模型进行偏好优化。

表5 二阶、三阶RSM模型的对比评估
极弧系数和槽宽对EMF的高阶响应曲面如图7所示,图7(a)与图7(b)分别为hap在低、高水平时的响应面,随着hap的增加,曲面下移,但其凸形形状没有改变,可以看出,αp在0.6附近时的EMF最大,此时ws变化对EMF影响很小。
图8为不同槽宽时αp和hap对THD的高阶响应曲面,2个曲面的形状和位置相似,当αp在0.6附近,单边气隙长度为1或0.6 mm时,THD最小。αp和ws对Tcog的高阶响应曲面如图9所示,随着单边气隙长度的增大,响应面在降低,曲面的弯曲程度也减小,当ws在9.5 mm附近,αp在0.6附近时,Tcog最小。

图9 优化参数的Tcog响应面Fig.9 Tcog response surface with optimized parameters
3.3 不同偏好对多目标优化结果的影响
将目标约束设为电机的设计要求阈值,表6为不同偏好目标与无偏好的优化方案,其有限元仿真结果如图10所示,均满足设计要求,偏好EMF方案的次要偏好目标皆逊于其它方案,而其他方案的EMF表现大致相同,偏好THD方案的Tcog优于无偏好,偏好Tcog方案的THD比无偏好的表现稍差,并且与无偏好方案相比,带偏好方案的主要偏好目标均更优异,体现了多目标偏好优化设计的优越性。

表6 不同偏好目标与无偏好的优化方案

图10 不同偏好方案与无偏好的有限元仿真结果对比Fig.10 Comparison of finite element simulation results between different preference schemes and non-preference schemes
4 NSGA-II偏好优化设计
4.1 NSGA-II优化
NSGA-II算法具有良好的全局搜索能力,已被广泛应用于多目标优化问题的求解[19]。本文采用文献[15]的加入随机罚函数与目标约束的NSGA-II对电机进行多目标偏好THD优化,加入偏好函数,设置偏好系数,初始种群数量为50,最大迭代次数为100,求出Pareto解和最优解,优化结果如图11所示。Pareto解虽然不满足目标约束,但具有良好的多样性,已明显偏向于设计要求。可行解与最优解均满足YSAFWG设计要求,两者相比,最优解的偏好目标THD表现最优异,可见采用该遗传算法进行多目标偏好优化设计的有效性。
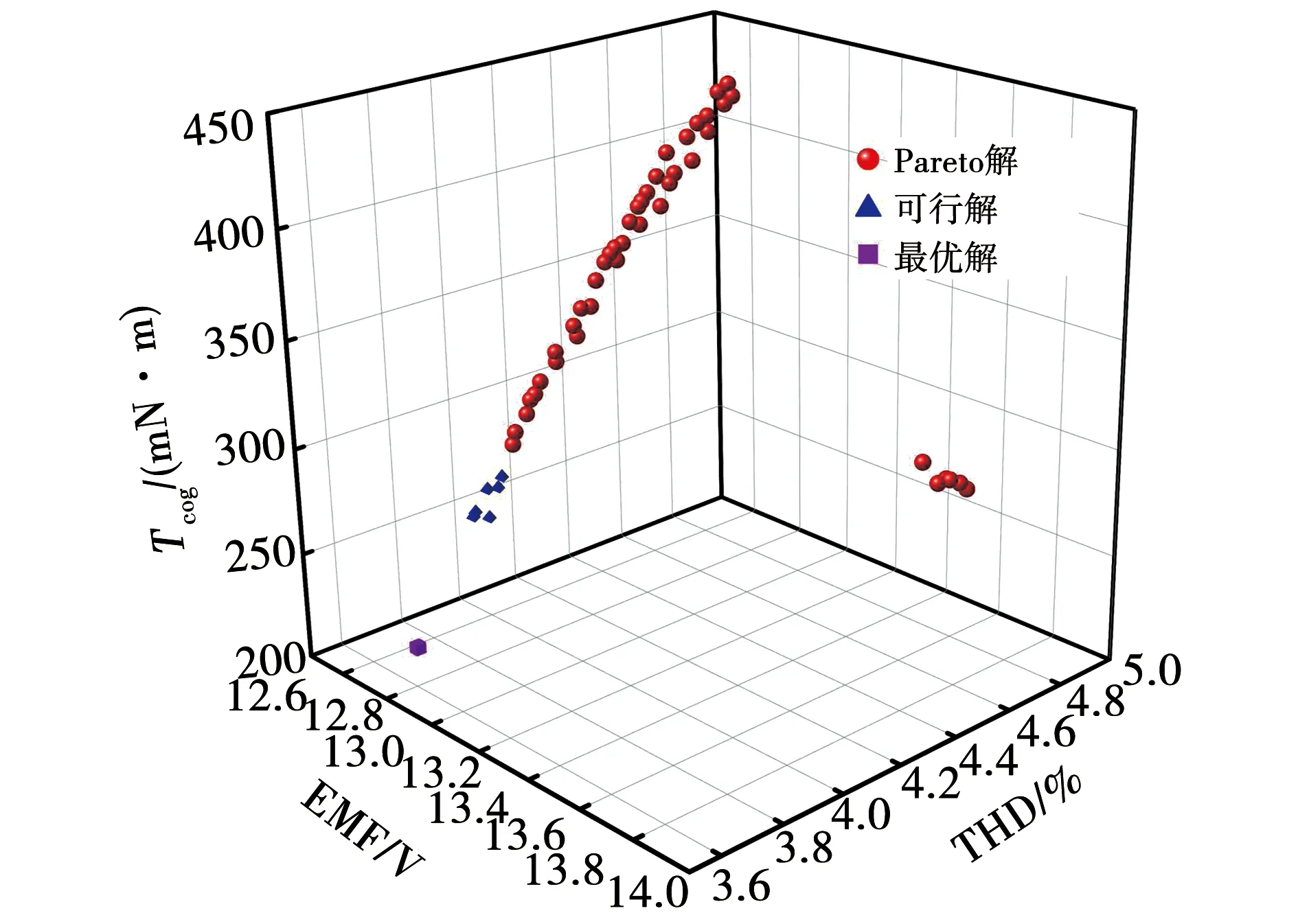
图11 经改进的NSGA-II优化结果Fig.11 Optimization result of improved NSGA-II algorithm
4.2 2种方法MOPO方案对比
结合高阶响应面和多目标遗传算法,得出以THD为主要偏好目标的优化方案如表7所示。利用有限元软件仿真验证,并计算电机的重量,结果对比如表8所示。

表7 2种优化方法的优化方案与优化前参数比较

表8 优化方案与优化前的有限元仿真结果比较
由表8可见,3个方案的重量相近,这是因为电机尺寸小,永磁体N25的密度与N35相近,电机的重量在优化中变化不大,均满足YSAFWG设计要求。原模型的电磁性能并没有达到设计要求,优化中加了目标约束,使得2种优化方法给出的方案均满足设计要求,并且方案2的各个目标值均比方案1优异,体现了改进后的NSGA-II在YSAFWG偏好优化设计上的优越性。
4.3 优选方案与原模型电磁仿真结果对比
根据分析,选择方案2作为最终优选方案,其与原模型的感应电动势谐波分布、齿槽转矩对比如图12、图13所示。优化后的EMF比原模型增大了8.45%,THD减少了74.59%,Tcog减少了38.92%。可见,优化后的电机性能大幅提高,以主要偏好目标THD表现最凸出,优化后仅为2.97%,体现了偏好优化设计的有效性。

图12 优化前后EMF谐波次数对比Fig.12 Comparison of EMF harmonics before and after optimization

图13 优化前后Tcog对比Fig.13 Comparison of Tcog before and after optimization
4.4 样机实验
根据优选方案制作样机,其定转子如图14所示,样机实验平台如图15所示。图15(a)为空载反电势测试平台,原动机拖动样机至额定转速600 r/min,测得一相空载反电势波形如图16所示,幅值为12 V,提取波形数据作傅里叶分析,谐波分布如图17所示,三次谐波占主要部分,其他高次谐波不明显,计算THD为4.09%。采用HBM扭矩传感器测试样机的齿槽转矩,该实验平台如图15(b)所示,得到结果如图18所示,齿槽转矩峰峰值为218.57 mN·m。对比实验结果与表8中优选方案的有限元仿真结果,两者吻合度较好,验证了YSAFWG理论分析和偏好THD优化设计的合理性。

图14 样机定转子结构图Fig.14 Topology of prototype

图15 样机实验平台Fig.15 Prototype experimental platform

图16 样机EMF测量波形Fig.16 EMF measurement waveform of prototype

图18 齿槽转矩测试曲线Fig.18 Test curve of cogging torque
5 结 论
本文采用高阶响应面法和经改进的NSGA-II优化设计了偏好THD的无磁轭模块化轴向磁通风力发电机。分析了YSAFWG的结构特点和电磁关系,通过有限元法分析了电机采用不同Mcpm的平均气隙磁密和相感应电动势,确定了周向充磁磁钢材料;与采用金属材料相比较,发现电机使用3D打印POM材料的重量减少了56.89%。在高阶RSM优化中,利用有限元仿真分析了不同偏好与无偏好的优化结果,体现了多目标偏好优化的优越性。最后,采用NSGA-II的偏好优化方案,与原模型相比,EMF增大了8.45%,THD减少了74.59%,Tcog减少了38.92%,通过有限元仿真与样机实验验证了YSAFWG多目标偏好优化设计的有效性和分析的正确性。

