基于参数在线辨识的高速永磁电机无差拍电流预测控制
刘刚, 张婧,2, 郑世强,2, 毛琨,2
(1.北京航空航天大学 惯性技术重点实验室,北京 100191; 2.北京航空航天大学 宁波创新研究院,浙江 宁波 315800)
0 引 言
随着稀土永磁材料的开发,基于矢量控制技术的永磁同步电机(permanent magnet synchronous motor,PMSM)以其优良的性能广泛应用于工业伺服驱动、电动汽车、新能源发电等领域[1]。永磁同步电机的高精度控制需要准确的转子位置信息和速度信息,但机械式传感器的使用具有安装维护困难、成本高、极高转速下响应速度有限等问题,因此,基于观测器的无传感器控制在高速永磁同步电机中得到了极大的发展[2],其中,滑模观测器(sliding mode observer,SMO)以计算简单、对外部扰动鲁棒性强等优势备受关注[3]。
永磁同步电机矢量控制一般为电流速度双闭环结构,电流环的动态和稳态特性是影响系统整体性能的关键因素,目前常见的电流环控制策略有滞环控制、比例积分(proportional integral,PI)控制和预测控制[4]。滞环控制具有电流响应速度快、鲁棒性强、易于计算等优点,但开关频率易受负载影响且电流纹波大[5]。相比之下,PI控制电流纹波小,可以有效降低稳态误差且开关频率固定,但数字控制的固有滞后特性会限制系统响应速度的提升,难以获取最优电流环带宽响应[6]。而基于离散模型的预测控制显示出良好的动态性能,能够在当前控制周期预测出下一周期的控制指令,提升系统带宽[7]。
预测控制通过系统模型来预测状态变量的未来行为,直接预测控制和无差拍预测控制是研究较为广泛的两种预测控制方法[8]。其中,直接电流预测控制通过最小化表示系统期望行为的成本函数来定义控制动作,电流动态响应最快,但开关频率可变,产生的电流纹波也最大[9]。无差拍预测控制具有固定的开关频率和良好的动态性能,无需开关状态评估和成本函数计算,计算负担大大降低[10-11]。但无差拍预测控制是基于离散模型的控制方法,需要准确电机模型参数和电机运行状态,而实际电机高速运行时,受温度升高、磁饱和等因素影响不可避免地会造成定子电阻、定子电感、永磁体磁链发生变化[12]。一方面,电机参数失配会导致电流谐波、电流跟踪偏差等问题,影响系统电流环的控制性能[13],另一方面,转子磁极位置估计的准确性决定PMSM无传感器控制系统的性能,电机参数失配会降低转子位置估计精度[14]。目前解决无差拍电流预测控制电流跟踪误差问题的常见方法有扰动观测器和参数辨识,为同时解决由于电机参数失配造成的电流跟踪误差和转子位置观测误差,对永磁同步电机进行多参数在线辨识并依次更新滑模观测器与无差拍电流预测控制器参数,是提高电流环控制性能和转子位置估计精度的重要策略[15]。
参数辨识是解决电机模型参数偏离原始设计值问题的一个重要手段,目前较为成熟的在线辨识方法有递推最小二乘法(recursive least squares,RLS)、模型参考自适应法、扩展卡尔曼滤波法等[16]。针对上述表贴式永磁同步电机无差拍电流预测控制器的参数不匹配问题,文献[17]提出一种基于模型参考自适应系统参数辨识的无差拍电流预测控制方法,解决磁链和电感参数不匹配的问题,然而未考虑定子电阻的识别,且寻找使辨识参数收敛的自适应律较为困难。文献[18]提出了一种改进的具有参数识别的PMSM无差拍电流预测控制方法,通过电流注入扰动观测器重构特征向量辨识定子电阻和定子电感,减小了计算负担却未考虑磁链参数的影响。上述方法只辨识了部分电气参数,不满足多参数在线辨识的要求。
针对基于反电势法进行转子位置估计易受参数摄动影响的问题,文献[19]运用扩展卡尔曼滤波器在线辨识内置式永磁电机的转子磁链和交轴电感,但未辨识电阻参数。文献[20]将电阻、电感辨识策略集成到位置观测器中,在αβ轴上施加高频正弦电压以识别d、q轴电感,在α轴上注入直流电压以识别电阻。对于表贴式永磁同步电机,文献[21]通过向d轴注入电流脉冲获取参数辨识所需数据,可以估计逆变器非线性引起的电阻误差、电感误差及永磁体磁链,但需要求解一个多元非线性回归问题。上述方法采用分时分步手段解决多参数在线辨识欠秩问题,但只考虑观测误差而未考虑到系数矩阵误差,忽略了参数之间的耦合影响。在实际应用中系数矩阵误差普遍存在,采用总体最小二乘法(total least squares,TLS)进行参数辨识可以同时考虑系数矩阵误差和观测误差,得到更精确的参数估计值,但直接求解TLS问题计算复杂,目前可以通过兴奋和抑制性神经元学习方法(excitatory and inhibitory learning, EXIN)进行在线迭代求取[22]。在TLS EXIN辨识电机本体参数的基础上,利用辨识结果更新电流环预测控制器和转子位置观测器参数,降低电机参数失配的影响。
针对表贴式永磁同步电机参数不匹配导致的电流跟踪偏差及转子位置观测误差,本文提出一种基于多参数在线辨识的无传感器高速永磁电机无差拍电流预测控制方法。首先推导出永磁同步电机的无差拍电流预测方程和基于反电势法的滑模观测器转子位置估计方程,分析电机模型参数误差引起的电流跟踪静差和转子位置估计偏差问题。为提高系统鲁棒性和稳态精度,采用基于TLS EXIN神经元求解的总体最小二乘法对电感、电阻及磁链参数分步辨识,在解决多参数在线辨识秩亏问题的同时,考虑观测误差和系数矩阵误差。根据辨识结果实时更新无差拍电流预测控制器和转子位置观测器参数。最后基于高速电机系统进行实验验证,结果表明本文所述方法能有效增强系统的鲁棒性,优化系统动态特性并提升系统控制精度。
1 无差拍电流预测控制
1.1 电流预测模型
本文以表贴式永磁同步电机为研究对象,为简化分析,假设三相PMSM为理想电机,在忽略电机的铁心饱和,不计电机涡流和磁滞损耗,转子上无阻尼绕组且相绕组中感应电动势波形为正弦波的前提下,PMSM在同步旋转坐标系下的电压方程为:
(1)
式中:ud、uq分别是定子电压的d、q轴分量;id、iq分别是定子电流的d、q轴分量;Ld、Lq分别是d、q轴电感分量;R是定子电阻;ψf是转子永磁体磁链;ωe是转子电角速度。
选定子电流为状态变量,对表贴式永磁同步电机有Ld=Lq=L,由式(1)可得PMSM的状态方程为:
(2)
使用前向差分对电流状态方程离散化,采样周期为T,得到永磁同步电机电流预测模型为:
(3)
1.2 无差拍电流预测控制原理
无差拍电流预测控制的结构框图如图1所示,将电流指令值i*(k+1)作为下一周期的电流预测值,与电机当前运行状态下的电流采样值i(k)一起代入式(3),计算使电机实际电流精确跟随指令值所需的电压矢量u(k),通过空间矢量脉冲宽度调制,生成所需要的开关信号作用于逆变器。速度外环仍采用经典的PI控制,所以无差拍预测控制系统依旧是双闭环系统,且与传统矢量控制结构接近,易在原有控制基础上实现。
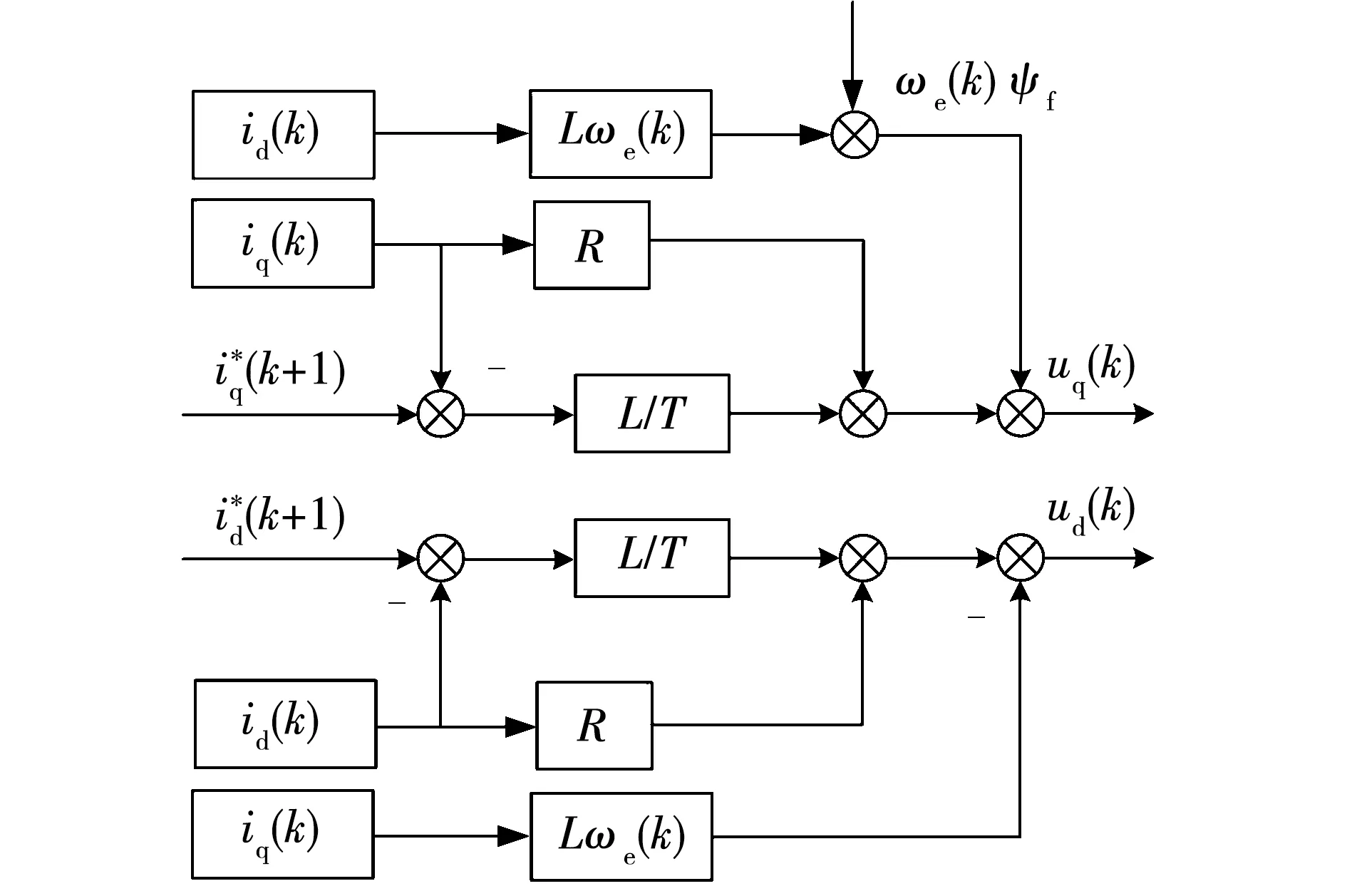
图1 PMSM无差拍电流预测控制结构框图Fig.1 Structure block diagram of PMSM deadbeat predictive current control
根据式(3),无差拍电流预测控制的输出电压矢量方程表示如下:
(4)

在2个连续的控制周期中,控制器在第1个控制周期根据当前电机的运行状态,使用控制器电机模型参数,计算出下一控制周期需要作用的电压矢量,其过程可以用式(4)表示。在第2个控制周期中,上一时刻计算得到的电压矢量作用于实际的电机模型,产生新的d、q轴电流,其过程如下:
(5)
其中R0、L0、ψf0分别代表电机实际电阻、电感和磁链参数。
将式(4)代入式(5),得到控制器电机模型参数偏离原始设计值时电流响应与给定的关系为:
(6)
式中ΔL、ΔR、Δψf分别为控制器电机模型参数与实际参数的差值,ΔL=L-L0,ΔR=R-R0,ψf=ψf-ψf0。
1.3 无差拍电流预测控制参数敏感性分析
无差拍预测控制是一种基于电机模型的预测控制方法,这意味着无差拍预测控制器具有参数敏感性,预测模型的精度将直接影响控制性能。
1.3.1 稳定性分析
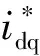
(7)
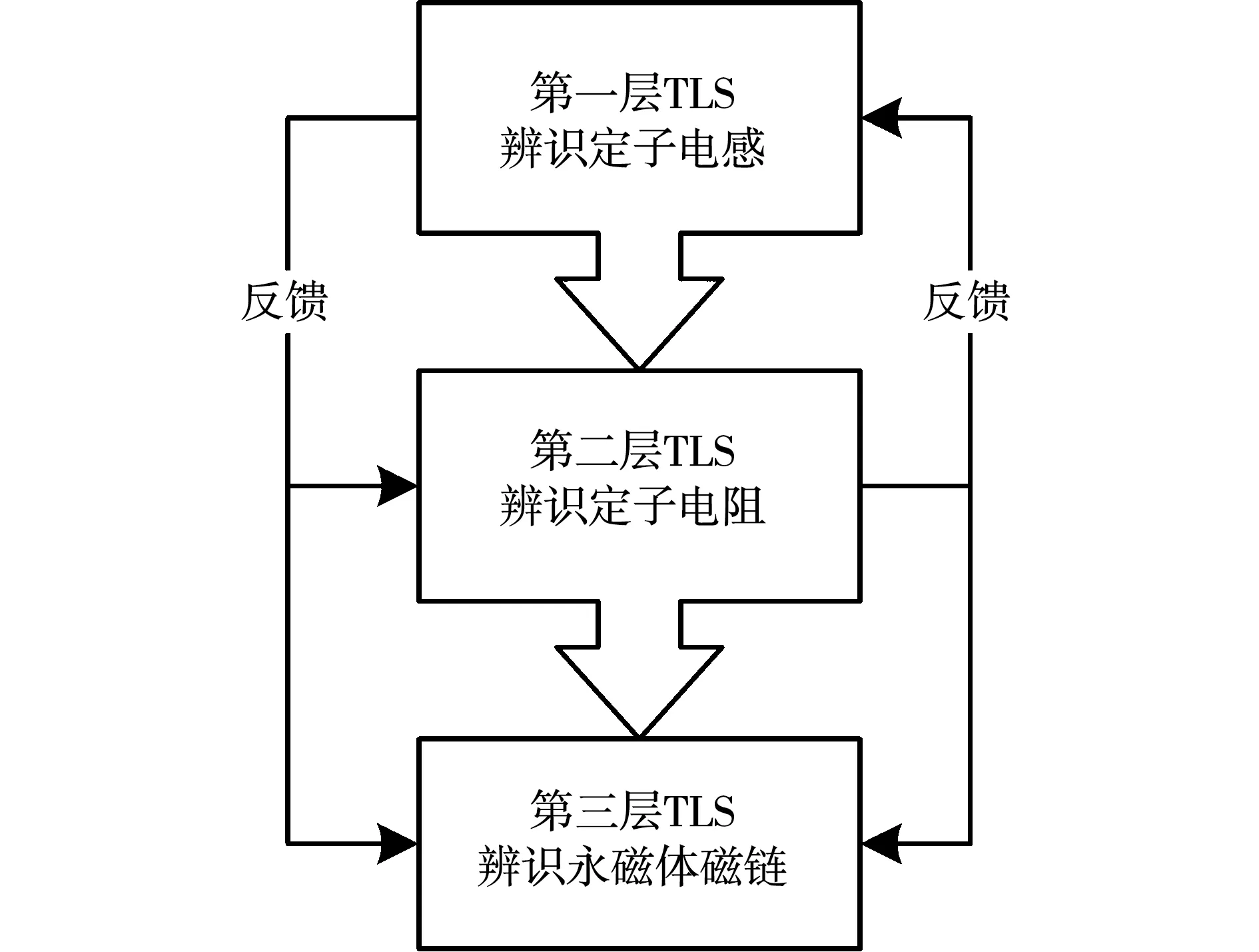
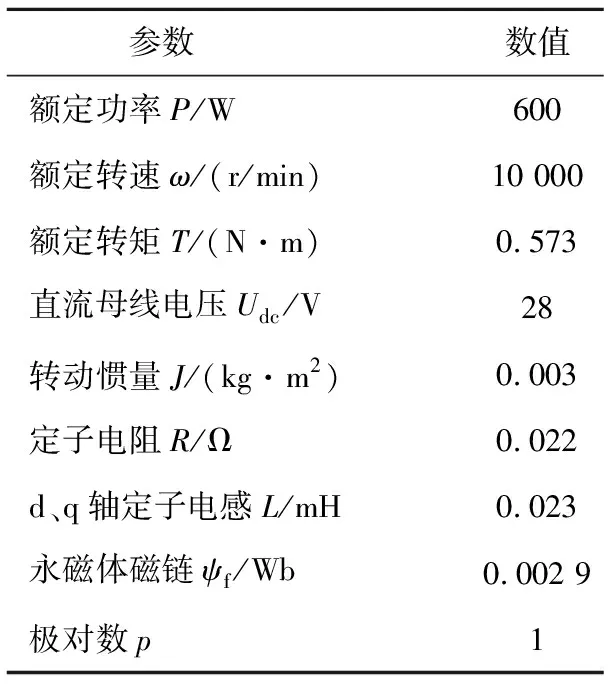
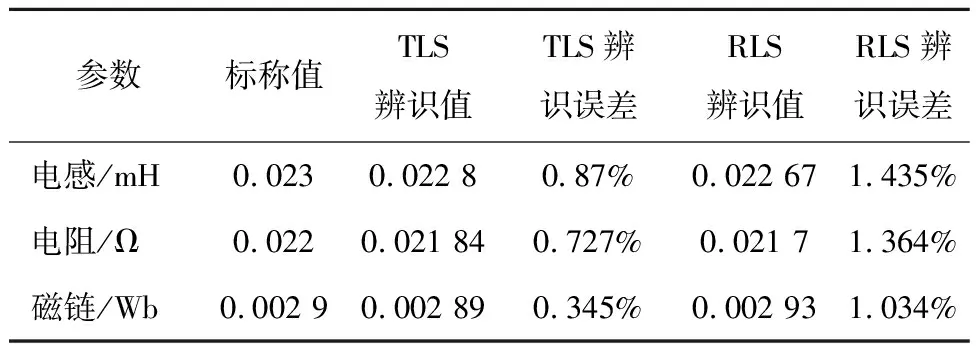
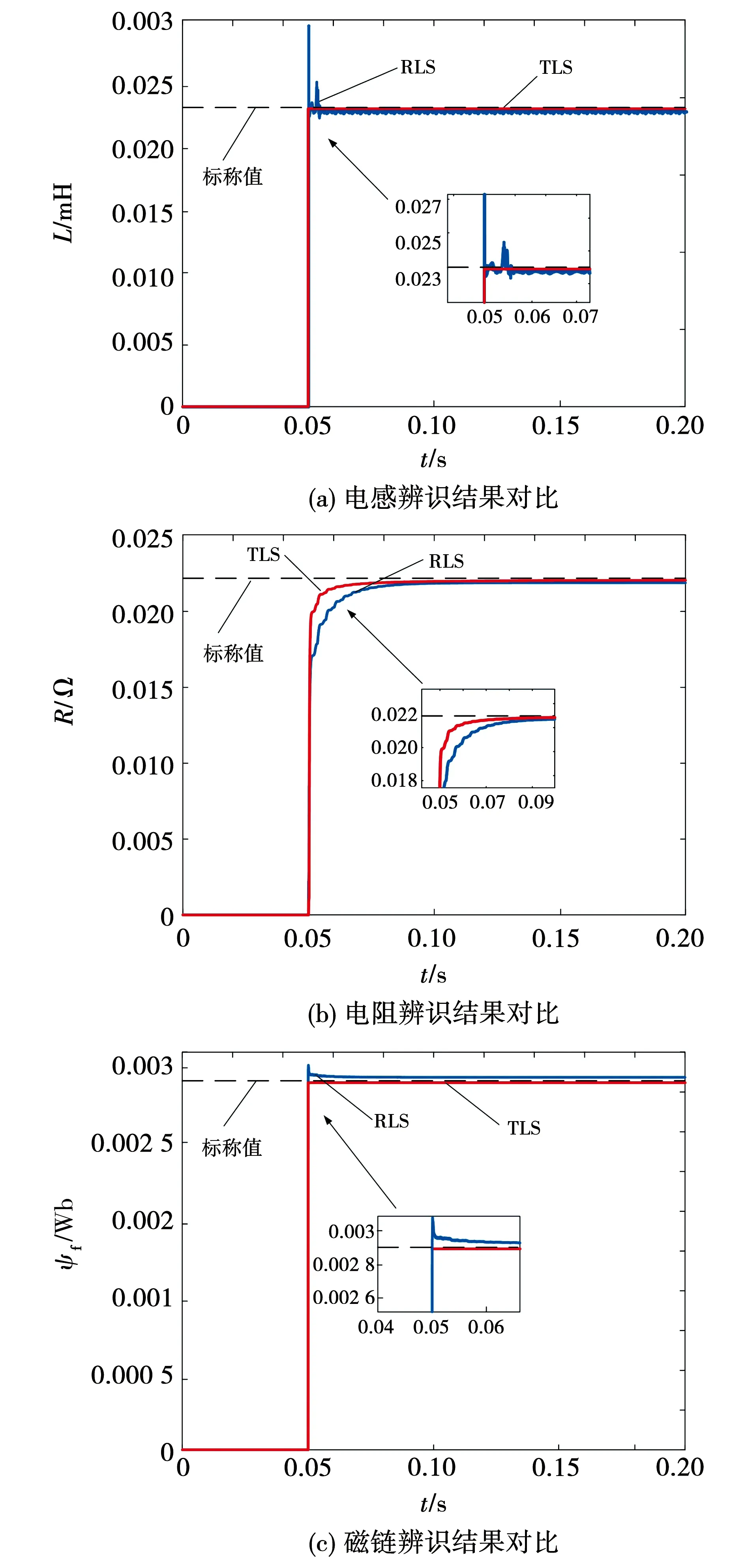
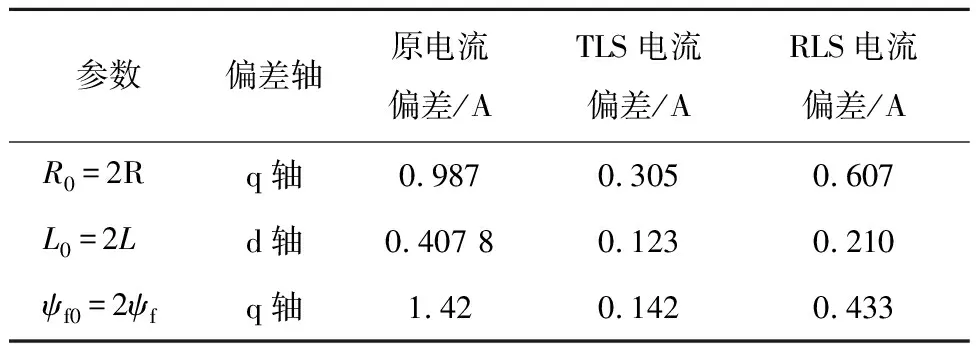
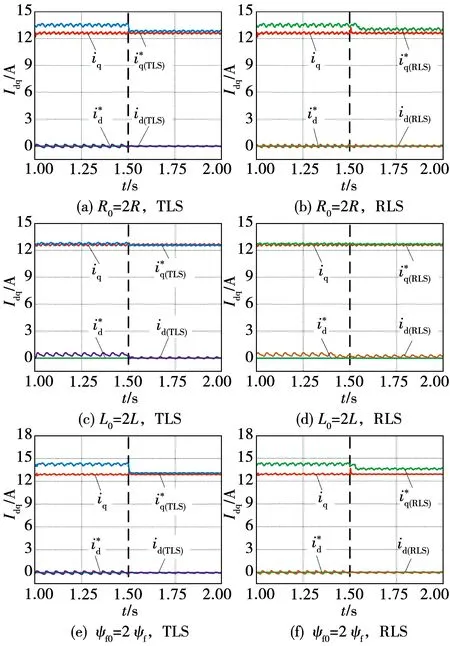
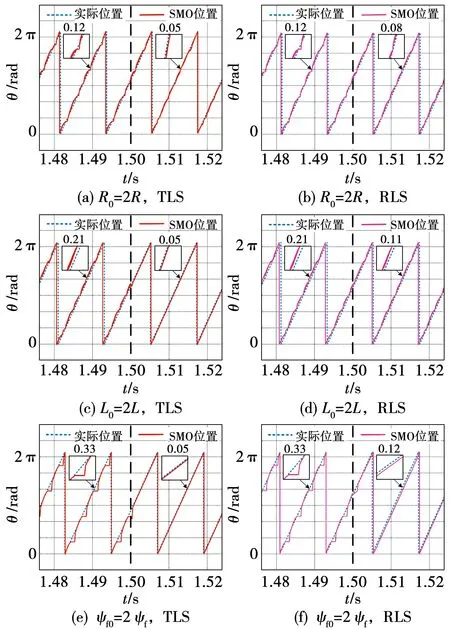
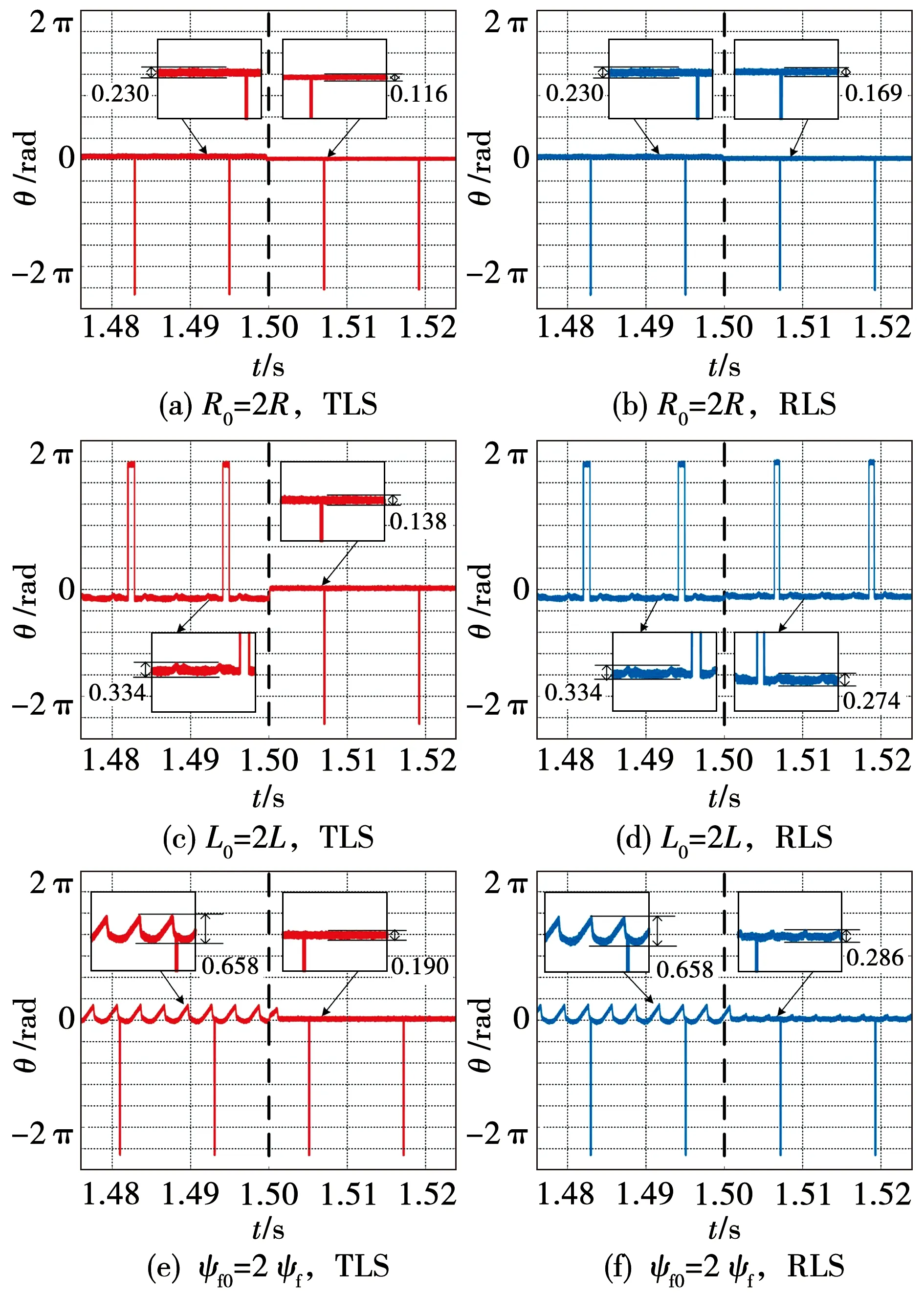
由闭环系统稳定性条件,其闭环极点必须位于单位圆内,由此得系统稳定性条件:0 1.3.2 稳态精度分析 当预测模型参数与电机实际参数存在偏差时,实际电流值不能跟踪给定电流值,导致电流控制出现静差。为分析电气参数不准确对电机电流控制性能的影响,在电机稳定运行时,认为采样周期足够小,有id(k+1)等于id(k),iq(k+1)等于iq(k),整理式(6)得电机稳定运行时d、q轴给定电流值和实际电流值受参数偏差影响的关系式为: (8) 由于采用id=0控制策略,因此与iq相比,id的作用基本可以忽略,式(8)中起主要作用的是含有电流iq的项,因此简化为: (9) (10) 表贴式永磁同步电机在两相静止坐标系下的电压方程为 (11) 其中:p=d/dt,为微分算子;uα、uβ与iα、iβ分别是定子电压和定子电流;Eα、Eβ为扩展反电动势,且满足 (12) 式中θ为转子角位置。由式(12)可以看出,扩展反电动势包含电机转子位置和转速的全部信息,为便于应用滑模观测器估计反电动势,基于PMSM定子电流方程的滑模观测器设计如下: (13) 采用反向差分变换法可得: (14) 设计滑模控制律为 (15) (16) 当观测器的状态变量达到滑模面Iα=0、Iβ=0后,观测器状态将一直保持在滑模面上,由滑模控制的等效原理,估计的反电势表示为 (17) 获取反电动势之后,通过反正切函数或者锁相环即可提取转子位置信息。 在电机高速运行时,采用滑模观测器实现转子位置估计,此时,式(16)中含有反电动势的项远大于另一项,因此含反电动势的项占据主导地位,由式(12)可知,该项与永磁体磁链有关,若将磁链辨识结果反馈至滑模系数中,可以减小位置估计误差。此外,式(14)含有与电阻、电感有关的项,若参数存在偏差在一定程度上也会降低位置估计精度,因此实现多参数在线辨识是解决参数不匹配问题、提高转子位置估计精度的重要手段。 永磁同步电机参数辨识的本质是利用输入、输出数据辨识电机参数。目前常用的参数辨识方法是递推最小二乘法,但是这种方法只考虑观测量误差,未考虑系数矩阵误差。另外,PMSM数学模型的状态空间秩为2,要辨识电阻、电感和磁链3个参数存在方程欠秩问题,因此提出在3种时间尺度下采用TLS方法在线分步辨识电气参数。 在实际应用中,系数矩阵误差普遍存在,通常采用最小二乘法或者RLS辨识方法只考虑观测量误差,但是忽略了系数矩阵误差,因此得到的参数估计值不再是最优无偏估计,降低了辨识精度和响应速度。而TLS算法不仅考虑到观测量误差,同时考虑了其余算法容易忽略的系数矩阵误差,因此,TLS在辨识结果的精度方面具有更加优秀的性能,其超调量相对RLS有所减小,且具有较快的响应速度和收敛速度。为提高参数辨识的准确性,选用TLS辨识算法进行研究。对于TLS回归参数的估计,常用的直接求解方法是奇异值分解,但求解计算复杂度较高,因此采用一种递归的TLS EXIN神经元算法求解TLS问题。 如图2所示为PMSM多参数辨识整体架构,其中,首先对变化较快的电感参数进行估计,然后估计定子电阻,最后估计变化较慢的磁链,辨识出的电感参数可以用于更新电阻和磁链,而辨识所得电阻参数可以用于更新电感和磁链,基于上述方法的多参数在线辨识同时考虑了观测量和系数矩阵的误差,在保证辨识精度的同时解决了多参数在线辨识的欠秩问题。 图2 PMSM多参数辨识整体架构Fig.2 Overall architecture of multi parameter identification of PMSM 当系数矩阵和观测向量都包含误差时,基于总体最小二乘算法的平差模型要优于普通的最小二乘算法,表示输入输出关系的回归方程可描述为 b+Eb=(A+EA)x。 (18) 其中:b为系统观测值向量;Eb为系统观测误差向量;A为系数矩阵;EA为系数误差矩阵;x为待估计参数向量。 TLS问题归结为解决以下优化问题: (19) 其中‖·‖F表示矩阵的Frobenius范数。 TLS EXIN神经元通过递归方式解决TLS问题,根据文献[23],通过最小化下式所示成本函数,可以得到TLS的解,即: (20) (21) x(k+1)=x(k)-α(k)γ(k)ai+ [α(k)γ2(k)]x(k)。 (22) 其中α(k)为学习率,是一个正常数函数,γ(k)定义为 (23) 式中δ(k)是一个时变函数,它依赖于每个采样时间计算的残差,定义为 (24) 对式(1)中d轴电压方程采用后向差分离散化,首先辨识电感参数,整理电感辨识模型为 aL(k)x1=bL(k)。 (25) 其中aL、x1、bL分别为系数矩阵、待辨识参数以及观测值向量,有: (26) 其次辨识电阻参数,根据离散化的d轴电压方程整理辨识模型为 aR(k)x2=bR(k)。 (27) 其中aR、x2、bR分别为: (28) 最后辨识磁链参数,根据离散化的q轴电压方程整理辨识模型为 aψf(k)x3=bψf(k)。 (29) 其中: (30) 为保证解的收敛性,应使辨识参数初值x(0)=0,在辨识电感参数时先假设式(26)所需电阻参数为常数,利用TLS辨识出电感稳态值后,再依次辨识电阻和磁链,式(28)中所需电感参数采用式(26)辨识结果,式(30)中所需电阻和电感参数采用式(26)和式(28)辨识结果,当本次电机参数辨识结果与上一次参数辨识结果之间的相对误差小于1‰,即可认为所辨识参数已经达到精度要求,此时可以停止迭代更新。 在中高转速阶段,采用基于反电动势的SMO实现转子位置估计,在启动阶段,电机的初始定位通过给定d轴电压实现强制定位,并且利用q轴电压开环拖动转子。如图3所示为基于参数辨识的无位置传感器高速永磁电机电流预测控制系统框图,在启动阶段通过电压开环拖动转子,当转速达到600 r/min时,切换到SMO进行转子位置估计。采用三层TLS算法分别对表贴式永磁同步电机的电感、电阻和磁链参数进行在线辨识,并将辨识结果分别反馈到电流环无差拍预测控制器及滑模观测器中,实现电流控制稳态性能和转子位置估计准确性的提高。 图3 基于参数辨识的无传感器PMSM无差拍电流预测控制系统框图Fig.3 Block diagram of PMSM deadbeat predictive current control system without sensor based on parameter identification 实验平台如图4所示,使用一台600 W,1对磁极的表贴式永磁同步电机,控制芯片选用TI公司的TMS320F28069,实验所用负载类型为叶轮负载,并且在转子轴上加装一个自研的增强型磁编码器以在实验中进行转子位置估计的准确性对比。 图4 实验平台Fig.4 Experimental platform 实验使用的永磁同步电机参数如表1所示。表1所示电机定子电阻初始值和d、q轴电感初始值采用IM3536 LCR测试仪离线测量得到,将LCR测试仪的探头分别接到电机三相线和中线上,即可获得电机的相电阻和相电感。而永磁体磁链初始值则通过反拖电机并根据下式计算获得,反拖转速为100 r/min,计算得到磁链值为0.002 9 Wb: 表1 永磁同步电机参数 (31) 其中:Ep是空载相反电势幅值;Elv是线反电动势有效值;KE是线反电动势常数;p是极对数。 为对比TLS和RLS两种算法的参数辨识效果,在电机稳定运行至10 000 r/min之后的0.05 s加入辨识算法,如图5所示为采用两种算法的参数辨识结果,表2为采用两种算法的辨识结果及与标称值之间的误差。 表2 电气参数辨识结果对比 图5 TLS与RLS辨识结果对比Fig.5 Comparison of TLS and RLS identification results 由图5以及表2可以看到,对于电感参数的辨识,RLS算法在辨识开始阶段波动较大,TLS辨识算法的收敛速度明显优于RLS,其辨识误差为0.87%,约为RLS辨识误差的二分之一;对于电阻参数的辨识,基于TLS的辨识算法在响应速度和辨识精度方面要优于RLS,其辨识误差为0.727%,而RLS辨识误差为1.364%;对于磁链参数的辨识,相比RLS算法,基于TLS算法的辨识误差更小,为0.345%。通过上述图表分析可以看出,TLS算法在表贴式永磁同步电机参数辨识过程中具有更快的收敛速度和更小的辨识误差。 为验证1.3节中DPCC的参数敏感性,同时对比验证TLS辨识算法的有效性,速度环采用传统的PI控制,电机负载转矩在额定负载0.573 N·m,转速为额定转速10 000 r/min。在10 000 r/min工况运行时,设置电机模型参数与本体参数不匹配,并在1.5 s分别加入2种辨识算法,将辨识结果反馈至电流预测控制器。 由于电机本体的参数不能任意修改设置,因此需要改变控制程序中的电阻、电感和磁链参数,以实现相应的参数不匹配,从而完成参数敏感性验证,同时通过RLS和TLS两种辨识算法的加入,对比验证TLS算法对提高电流稳态控制性能的有效性。图6为TLS与RLS两种算法的控制器电流响应对比,表3为TLS与RLS的dq轴电流响应误差对比。 表3 两种辨识算法dq轴电流响应误差对比 图6 参数偏差存在时,TLS与RLS电流响应对比Fig.6 Comparison of TLS and RLS current response with parameter deviation 由图6结合表3可知,1.5 s之前预测控制器参数与电机实际参数之间存在偏差,导致dq轴电流响应存在静差,电流静差情况与1.3节理论分析一致,且磁链偏差对控制电流影响最大,在1.5 s时,分别采用TLS和RLS进行参数辨识,并将辨识结果注入无差拍电流预测控制器中,图6(a)、(c)、(e)为采用TLS的电流响应波形,图6(b)、(d)、(f)为采用RLS的电流响应波形。当实际磁链为给定值两倍时,q轴电流偏差可达1.42 A,1.5 s加入TLS辨识算法后,电流静差减小到0.142 A,采用RLS算法的电流静差为0.433 A;当实际电阻为给定值2倍时,q轴电流偏差为0.987 A,加入TLS辨识算法后,偏差减小为0.305 A,使用RLS的电流静差为0.607 A;实际电感为两倍给定值时,d轴电流偏差为0.407 8 A,加入TLS后偏差减小至0.123 A,加入RLS后偏差减小至0.210 A。由上述分析可知,控制器电机模型参数不匹配导致dq轴电流响应产生偏差,TLS和RLS两种辨识算法都能有效降低电流响应误差,经由对比可以验证,TLS的响应速度更快,且稳态电流偏差更小。 图7为PMSM参数存在偏差时,分别采用TLS和RLS两种辨识算法的转子位置波形比较。 图7 参数偏差存在时,TLS与RLS转子位置估计波形对比Fig.7 Comparison of TLS and RLS rotor position estimation waveforms with parameter deviation 为验证SMO参数不匹配对转子位置估计的影响,并对比验证TLS辨识算法的有效性,设定实验条件与4.2节一致,滑模观测系数为0.3。在10 000 r/min工况运行时,设置电机模型参数与本体参数不匹配,并在1.5 s各自加入TLS和RLS,将辨识结果反馈至SMO。 由图7可以得到,1.5 s之前,由于SMO参数与电机实际参数存在失配,导致SMO估计的转子位置与磁编码器实际输出的转子位置之间存在角度误差,因此SMO位置估算无法准确跟踪磁编码器检测的实际转子位置。在1.5 s分别通过TLS和RLS进行参数辨识,并将辨识结果注入SMO,图7(a)、(c)、(e)为采用TLS的转子位置波形,图7(b)、(d)、(f)为采用RLS的转子位置波形,可以看出,1.5 s加入辨识算法后,SMO位置估计误差明显减小,且通过对比可以发现,采用TLS可以获得更小的位置估计误差。 将SMO估计位置与磁编码器检测位置作差得到转子位置观测误差,图8为PMSM参数存在偏差时,分别采用TLS和RLS两种辨识算法的转子位置观测误差对比。 图8 参数偏差存在时,TLS与RLS转子位置观测误差对比Fig.8 Comparison of TLS and RLS rotor position observation errors with parameter deviation 加入辨识算法之前,转子位置观测误差较大,在1.5 s分别通过TLS和RLS进行参数辨识,并将辨识结果注入SMO,图8(a)、(c)、(e)为采用TLS的位置观测误差波形,图8(b)、(d)、(f)为采用RLS的位置观测误差波形。结合图7可知,磁链偏差对转子位置估计影响最大,当电机实际磁链是SMO磁链的2倍时,位置观测误差波动可达0.658 rad,通过TLS更新SMO后,观测误差波动减小为0.190 rad,采用RLS后波动减小为0.286 rad;其次影响较大的是电感偏差,当电机实际电感是SMO电感的2倍时,观测误差波动为0.334 rad,通过TLS更新SMO后,观测误差波动减小为0.138 rad,采用RLS后波动减小为0.274 rad;电阻偏差对SMO观测误差的影响较小,当电机实际电阻是SMO电阻两倍时,观测误差波动为0.230 rad,通过TLS更新SMO后,观测误差波动减小为0.116 rad,采用RLS后波动减小为0.169 rad。 由此可见,SMO电机模型参数与实际电机参数存在偏差时,会导致转子位置估计存在一定程度的偏差,且磁链偏差对位置观测误差的影响较大。TLS与RLS均可修正电机参数偏差,提高转子位置估计的准确性,通过对比验证,采用TLS具有更小的转子位置观测误差。 本文提出了一种基于参数辨识的无传感器高速永磁电机无差拍电流预测控制方法,采用TLS EXIN神经元求解的参数在线辨识算法,兼顾了系数矩阵误差和观测量误差,可以实现无差拍电流预测控制参数敏感性的抑制,并对预测控制器和滑模观测器的电阻、电感和永磁体磁链进行在线修正,进而实现dq轴电流以及转子位置的准确跟踪。相比于传统预测控制方法,有效地抑制了参数敏感性,具有更好的稳态性能,同时,相比于普通滑模观测器,进一步提升了转子位置估计精度。
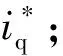
2 基于滑模观测器转子位置估计
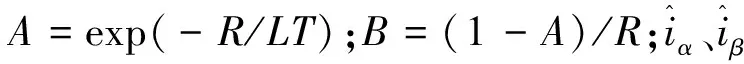
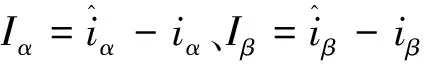
3 PMSM多参数在线辨识
3.1 TLS辨识算法
3.2 TLS多参数辨识架构
3.3 基于TLS的多参数在线辨识算法
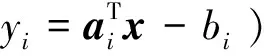

4 实验结果及分析

4.1 TLS与RLS参数辨识比较实验结果
4.2 加入TLS参数辨识对电流控制性能的影响
4.3 加入TLS参数辨识对转子位置估计的影响
5 结 论

