一类拟线性方程Cauchy问题的可解性

金启胜

(安庆职业技术学院,安徽 安庆 246003)

0 引言

在变分法、质点力学和几何光学中都出现了一类方程,它们的特点是其通解可以通过解一个常微分方程组而得到,这种方法称为特征线法。下面仅讨论两个自变量的拟线性方程,但所有理论和方法可以完全类似地推广到多个自变量的情况。

考察拟线性方程

a(x,y,u)ux+b(x,y,u)uy=c(x,y,u)

(1)

这里u=u(x,y),(a(x,y,z),b(x,y,z),c(x,y,z))是方程(1)的特征方向。方程(1)的特征曲线是指处处与特征方向相切的曲线。如果特征曲线的参数方程设为x=x(t),y=y(t),z=z(t),那么就有

也就是

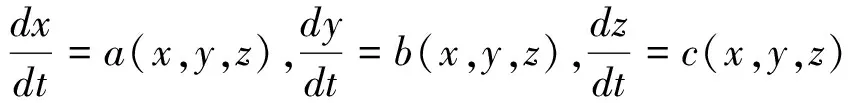
(2)

我们把(2)式称为(1)的特征方程。方程(1)的积分曲面是指处处与特征方向相切的曲面,即z=u(x,y)。显然,方程(1)的解就是积分曲面z=u(x,y)。

1 主要结论及证明

定理1如果特征曲线γ上有一点P(x0,y0,z0),且该点落在积分曲面S:z=u(x,y)上,那么特征曲线整个位于积分曲面上。

证明假设特征曲线γ的参数方程为x=x(t),y=y(t),z=z(t),易知,它是方程组(2)的解。而且对某一个参数t=t0有x0=x(t0),y0=y(t0),z0=z(t0)=u(x0,y0),由条件可得P=(x(t0),y(t0),z(t0))∈S。

设U=U(t)=z(t)-u(x(t),y(t)),根据P∈S,得到U(t0)=0。结合(2)有

=c(x,y,z)-uxa(x,y,z)-uyb(x,y,z)

所以有

-ux(x,y)a(x,y,U+u(x,y))

-uy(x,y)b(x,y,U+u(x,y))

(3)

这里x=x(t),y=y(t)。因为(1)的解为z=u(x,y),所以(3)的解是U=0。由常微分方程Cauchy问题解的唯一性定理可知,根据U(t0)=0得到U(t)≡0,也就是z(t)≡u(x(t),y(t)),故γ∈S。定理1得证。

定理2如果γ:(x,y,z)=(f(s),g(s),h(s))是光滑曲线,满足如下条件

1)f′2+g′2≠0;

2)P0=(x0,y0,x0)=(f(s0),g(s0),h(s0))处行列式不等于零,即

J=|f′(s0)a(x0,y0,z0)g′(s0)b(x0,y0,z0)|≠0;

(4)

3)a(x,y,z),b(x,y,z),c(x,y,z)在曲线γ附近光滑。

那么Cauchy问题:

{a(x,y,z)ux+b(x,y,z)uy=c(x,y,z)

u(f(s),g(s))=h(s)

(5)

在s=s0某一个邻域内的解是唯一的。

证明在s0某一个邻域内求特征方程(2)的解,也就是在|s-s0|<δ,δ>0中求

x=X(s,t),y=Y(s,t),z=Z(s,t)

(6)

使等式(x,y,z)=(f(s),g(s),h(s))在t=0时成立即可(|s-s0|<δ,0≤t

Xt=a(X,Y,Z),Yt=b(X,Y,Z)

Zt=c(X,Y,Z)

(7)

X(s,0)=f(s),Y(s,0)=g(s)

Z(s,0)=h(s)

(8)

根据J≠0和隐函数定理,从(6)的第一、第二个式子求出函数s=S(x,y),t=T(x,y),在|s-s0|<δ1,0≤t≤T1时有S(x0,y0)=s0,T(x0,y0)=0成立,所以Cauchy问题(5)的解就是

z=Z(S(x,y),T(x,y))=u(x,y)

(9)

其实,我们令δ*=min{δ,δ1},T*=min{T,T1},那么在|s-s0|<δ*,0≤t≤T*时就有

Z(S(x,y),T(x,y))|t=0=Z(s,0)=h(s)

所以h(s)=u(f(s),g(s))。故(9)满足Cauchy问题(5)。

我们对(9)依次求偏微商可得

Zx=ZsSx+ZtTx,Zy=ZsSy+ZtTy

(10)

再对x=X(s,t),y=Y(s,t),z=Z(s,t)第一、第二个式子关于x求偏微商可得

(11)

(11)中Δ=XsYt-XtYs≠0,因为J≠0。再关于y求偏微商可得

(12)

把(11)式和(12)式代入(10)式,再把Zx=ZsSx+ZtTx乘以a(X,Y,Z),加上Zy=ZsSy+ZtTy乘以b(X,Y,Z)得到

[a(X,Y,Z)Zx+b(X,Y,Z)Zy]Δ

=(ZsYt-ZtYs)a+(ZtXs-ZsXt)b

最后将a,b,Δ代入并化简得到

a(X,Y,Z)Zx+b(X,Y,Z)Zy=c(X,Y,Z)

所以u(x,y)=Z(S(x,y),T(x,y))是Cauchy问题(5)的解。该邻域内有解得证。结合定理1,通过曲线γ的积分曲面一定包含通过曲线γ上各点的特征曲线,故一定包含曲面(6),亦即该邻域内存在唯一解。定理2得证。

2 关于结论的几点补充说明

说明3关于n元函数u=u(x1,x2,…,xn)的拟线性方程为

对应的常微分方程组是

(13)

(14)

过γ上每一个具有参数(s1,s2,…,sn-1)的点作特征曲线,即求出(13)的当t=0时等于(f1,f2,…,fn,h)的解

(15)

在条件

J=

≠0

(16)

之下,就能由(15)前n个式子解出s1,s2,…,sn-1,t,将它们代入(15)的第n+1个式子,就得到积分曲面z=u(x1,x2,…,sn),它就是Cauchy问题(5)的解。