三星编队TDOA定位精度分析

宋小勇,毛 悦,宗文鹏,王 龙,冯来平

1. 地理信息工程国家重点实验室,陕西 西安 710054; 2. 西安测绘研究所,陕西 西安 710054

随着全球化的发展,采用无线电进行通信和导航的用户数量不断增加,用户分布范围也在全球拓展。非法使用或恶意干扰无线电资源成为制约无线电技术应用发展的突出问题,为了实现对全球范围内非合作用户的有效管控,需要及时掌握用户频谱、位置等信息。远洋船采用的海事自动识别系统虽能及时通报船舶位置,但该系统不能应对由于信号恶意关闭或蓄意信息欺骗造成的目标真实位置不确定问题。出于军事或其他目的,敌对方经常通过恶意发射大功率信号对卫星导航或其他军民用通信信号进行干扰,这些人为干扰源运动范围大,采用传统的陆基干扰源监测定位方法,干扰源定位精度受地面环境遮挡影响严重,同时,陆基或海基探测定位方法受海域空域限制,难以实现对目标连续跟踪。为此,世界各国竞相发展天基无线电信号源定位系统[1-2]。利用卫星探测并定位无线电发射源是大范围管控无线电用户的高效方式。该方法可实现对全球大部分地区主动发射无线电信号的非合作目标的监控。对于远海、沙漠等人烟稀少地区,利用卫星探测是唯一现实可行的技术。

天基无线电监测管理核心技术之一是如何利用被动无线电测量确定信号源位置。精密无线电测向和信号到达时间差、到达频率差测量(TDOA/FDOA)是目前使用最多的无源定位技术,相比测角而言,TDOA/FDOA技术测量精度和可靠性更高[3-9],因此,以美国鹰眼360为代表的无线电定位卫星大多采用该技术。近年来,国内外采用TDOA观测确定信号源位置方面,产生了大量研究成果。针对TDOA定位解算中出现的非线性问题,文献[10]提出两步最小二乘处理策略,将非线性问题转化为两步线性问题,该方法极大减小了数据处理运算量,降低了发射源点位坐标初值精度要求,但解算结果是近似最优解,且不便于使用外部约束。文献[11]构建了综合考虑卫星位置误差影响的统一形式半定规划定位算法,但算法实现过于复杂,实用性受限。文献[12]针对鹰眼360星座构型,分别采用几何法及两步最小二乘法仿真了TDOA定位精度,两种方法精度一致,均能够实现优于千米级无源定位精度。但该文献定位仿真研究仅限于单历元定位,未分析多历元观测量对定位结果的贡献。考虑到三星编队在卫星构型设计和建设运行成本上的优势,本文重点开展三星编队卫星对地面静态信号源的多历元TDOA无源定位方法研究,并对比分析其与单历元定位方法的精度优势。

1 定位模型及方法

1.1 定位观测方程

利用天基TDOA/FDOA测量实现信号源定位本质采用的是多个双曲面空间交汇定位原理。通过测量无线电信号到达两个接收卫星的时间差,可确定同一信号发射源到两个接收卫星距离差。已知两个接收卫星瞬时位置和信号到达时间差观测量后,信号源位置即位于以两个卫星位置为焦点的空间双曲面上[12]。通过对不共线4个以上卫星信号到达时间差测量,可形成3个独立的距离差观测量,每个距离差观测方程对应一个空间双曲面,3个空间双曲面交点即可确定目标点位置。通常多个空间双曲面交点不唯一,需要通过其他辅助信息确定信号源真实位置。如果仅有3个监测卫星,对于每个信号源,单历元观测量只能形成两个独立距离差观测方程,只能确定一条空间曲线,不能确定目标点三维位置,目标定位需要附加额外约束条件。

两个卫星对同一信号源距离差观测方程形式如下

d12=r01-r02+c(Δt1-Δt2)+Δtrop01-

Δtrop02+Δion01-Δion02+ε12

(1)

式中,d12为距离差观测量;r01、r02分别为信号源到两个卫星的距离;Δt1、Δt2为卫星钟差;Δtrop01、Δtrop02为信号对流层延迟误差;Δion01、Δion02为电离层延迟误差;ε12为TDOA测量噪声。

由式(1)可知,影响距离差测量精度的因素包括卫星位置误差、卫星钟差、对流层、电离层路径延迟误差及测量噪声。对于由编队卫星组成的监测系统,由于同组内不同卫星相对地面信号源传播路径接近,对流层、电离层影响经过路径差分后可基本消除[13-14]。采用星载GNSS对编队卫星进行精密定轨和时间同步处理,利用后处理精密GNSS卫星轨道及钟差产品,低轨卫星位置误差可优于5 cm,星间时间同步精度优于0.2 ns[15-19]。采用星载数据处理软件利用GNSS快速轨道产品进行实时处理,低轨卫星轨道精度在分米级,时间同步精度优于2 ns[20-22]。综上所述,卫星位置、钟差及对流层、电离层残余误差对距离差影响小于米级。TDOA测量噪声可按照式(2)估计[12,23-24]

(2)

式中,β为信号带宽;βn为接收机噪声带宽;T为积分时间;S/N为输入信噪比;c为光速;βnT(S/N)为输出信噪比。当信号带宽为10 MHz,输出信噪比为16时,TDOA测量精度近似为2.9 m。

综上,若采用星载GNSS技术对监测卫星进行精密定轨和时间同步,影响TDOA测量精度的主要误差源为信号测量噪声。随后仿真试验以测量噪声3 m作为测量噪声仿真输入条件。

1.2 三星单历元定位解算方法

采用三星编队卫星实现信号源定位是目前使用较多的定位技术。采用三星编队监测时,若监测卫星采用星载GNSS进行定轨,可不考虑监测卫星轨道误差、时间同步误差和路径传播误差,此时在惯性坐标系中TDOA定位观测方程简化如下

(3)

(4)

式中,r01、r02、r03为信号源与卫星之间距离;d12、d13为距离差观测量;ε12、ε13为测量噪声;x0、y0、z0分别为发射时刻信号源位置;xi、yi、zi为接收时刻卫星位置。在地固坐标系中,上述方程需要考虑地球自转改正。对于地面静态信号源,任意观测历元,上述TDOA方程3颗卫星形成两条独立基线,两个独立基线对应两个独立星间距离差观测方程,包含3个信号源空间位置参数,测量方程不可解。为此,需要增加额外的约束条件。按照增加约束的条件方法,可分为多种解法。一种是增加监测卫星数量,通过增加独立观测数量解决测量秩亏问题[7,9]。另一种方法则通过增加信号源高程信息约束,增加一个约束方程,消除测量秩亏问题。

在地固坐标系中,地面信号源位置通常用地固椭球坐标系三分量表示,高程约束信息为椭球高。已知信号源高程信息后,信号源三维位置坐标满足下述椭球约束方程

(5)

式中,N为测量点对应参考椭球法线长度;f为参考椭球曲率;x0、y0、z0为未知信号源位置参数;h为信号源已知高程约束信息。综合式(3)、式(4)2个星间距离差观测方程和1个椭球约束方程,可形成包含3个未知参数的3个非线性观测方程。采用非线性方程迭代求解方法或带约束参数平差方法,可得到信号源位置信息。

利用测站大地坐标与直角坐标之间的转换关系,通过对测站高程求导,可得到测站高程误差影响信号源位置误差的近似估计公式

(6)

式中,dh为测站高程误差;dx、dy、dz为测站直角坐标三分量误差;φ、λ为测站大地经纬度。

上述方法需要已知信号源高程位置信息。对于海面位置信号源,其高程信息可近似设置为0。而对于陆地平坦地区目标,则需要结合信号源近似位置信息,通过辅助采用数字高程信息确定信号源准确位置。实际计算过程中需要通过多次迭代计算获取准确位置。对于地形复杂地区,此方法很难收敛。

1.3 三星多历元定位解算方法

尽管利用单历元3颗卫星形成的两个独立TDOA观测量结合信号源高程信息约束可确定信号源三维位置。但当信号源在地形复杂区域或空中时,其高程信息很难准确获取,导致上述单历元定位方法难以应用。增加卫星数量则面临增加成本及轨道优化控制问题。在不增加监测卫星数量前提下,对于地面静止信号源或运动轨迹相对规律的信号源,如果能够实现多次测量,可利用多个历元观测量,通过多历元联合求解方法解决观测量秩亏问题。对于3颗监测卫星组成的编队卫星,多历元联合解算方法简述如下。

不考虑卫星位置误差及信号传播误差,在惯性坐标系3颗卫星t时刻TDOA观测方程为

r0i(t)-r0k(t)=dik(t)+εik

(7)

(8)

(9)

Δti=r0i/c

(10)

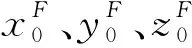
已知监测卫星位置和坐标转换矩阵M(t),组合多个历元距离差观测量,可形成仅包含信号源在地固坐标系中位置参数的非线性方程组,采用非线性最小二乘估计方法,通过对上述方程对应的线性化观测方程迭代求解可得到位置参数最优估值。

首先,利用信号源初值位置对式(7)进行线性化,得到线性化方程如下

(11)

组合多个历元线性化观测方程,采用最小二乘估计方法,可得到信号源位置改正量。利用改进的信号源位置进行迭代计算,收敛后可得到信号源位置最优估计值。多历元TDOA解算不需要信号源辅助信息,但其动态定位能力弱,对于高速复杂运行信号源定位需要FDOA信息支持。

1.4 信号源定位PDOP值计算

利用TDOA实现信号源定位,其定位精度与距离差测量精度和定位几何构型相关。为评价定位几何构型影响,借鉴GNSS定位几何构型的PDOP值计算原理,天基TDOA距离差观测定位几何构型影响也可用PDOP值评估,可用线性化距离差观测方程对应的法方程的逆矩阵计算,用法方程逆矩阵对角线元素之和的平方根来表征。假设线性化后TDOA观测方程为

L=AΔX+ε

(12)

则定位PDOP定义为[13,25]

(13)

对于具有高程约束的TDOA定位,其PDOP计算需要利用带约束平差方法计算点位坐标协方差阵,然后计算对应PDOP值。由于矩阵M为正交矩阵,因此对于多历元TDOA定位,坐标转换矩阵M并不影响定位PDOP值评估结果。

2 仿真试验分析

2.1 仿真试验条件

为验证基于三星编队卫星TDOA定位方法的合理性,分析信号源定位精度,本文采用模拟观测数据进行多方案仿真定位分析。由于编队卫星精密轨道及钟差确定已有相对成熟的方法,本文重点在于分析定位几何构型影响。为简化分析,本文三星编队卫星标准轨道仿真采用二体运动动力学模型,未考虑地球非球型引力和其他摄动力影响。地球自转运动模型仿真也仅考虑地球自转主项,不考虑岁差、章动、极移等因素影响[14]。轨道仿真采用3颗卫星组成的编队,3颗卫星空间构型设计需要综合考虑三星波束重叠覆盖范围、编队卫星构型维持需要的轨控成本、覆盖区定位精度等因素。参考鹰眼360星座构型,采用一高两低三星编队。两颗较低轨道卫星位于同一轨道面内,相距近250 km,轨道高度575 km。另一颗卫星轨道高度600 km,位置经度位于前两颗卫星之间,与其构成近似等边三角形构型,其轨道根数中的升交点经度围绕前两颗星轨道对应参数周期变化。三颗卫星均为太阳同步轨道卫星。这种卫星编队的优点是轨控次数少,能保证覆盖区大范围定位精度,缺点是沿星下点区域定位几何构型较差。仿真采用的三星编队卫星轨道根数见表1。

表1 仿真轨道根数

上述轨道根数能够保证除极区外,卫星编队保持近似等边三角形构型,空间构型如图1所示。

图1 三星编队卫星构型Fig.1 A cluster of three satellites

由上文可知,观测数据仿真未考虑卫星轨道、星间时间同步误差,同时也忽略了信号传播路径延迟等系统性误差对距离差观测量影响,将上述残余随机误差等效到测量噪声中,仿真距离差测量噪声选择为3 m随机噪声。在单次测量信号覆盖范围方面,参考国外卫星载荷特性,将每颗监测卫星接收天线对地覆盖范围的直径近似取为1000 km,对应地球表面经纬度范围约为4.48°。考虑到低轨卫星运动的周期性,定位几何构型变化也具有周期重复特性,因此,仿真计算采用的数据时段长度选择为1个轨道周期。

2.2 3颗卫星单历元定位结果

基于上述仿真编队卫星构型,分别在赤道及中纬度地区选择2个卫星轨迹星下点,首先计算上述星下点周边半径500 km范围内标准椭球面格网点,然后利用仿真轨道和仿真观测模型仿真3颗卫星对每个格网点距离差观测量数据,利用单历元距离差数据和卫星轨道数据,采用结合高程信息约束的三星单历元定位解算方法计算信号源位置,并计算信号源位置与对应仿真理论值之间三维位置误差和误差分布。结果如图2—图5所示。

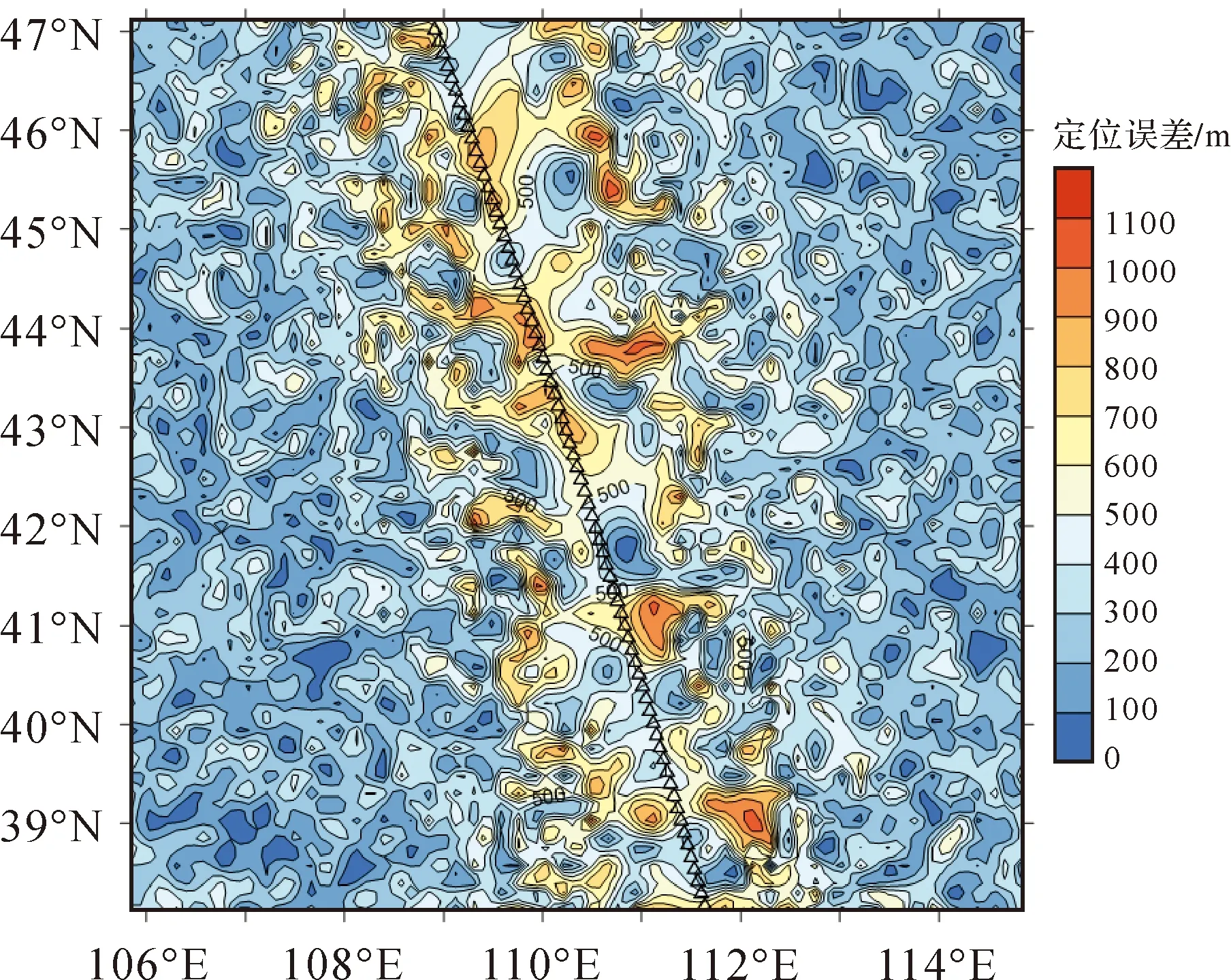
图3 单历元中纬区定位误差等值线Fig.3 Geolocation errors contour of medium latitude for single epoch

图4 单历元低纬区定位误差分布Fig.4 Distribution of geolocation errors of low latitude for single epoch

图5 单历元中纬区定位误差分布Fig.5 Distribution of geolocation errors of medium latitude for single epoch

为定量分析星下点周边不同区域定位误差分布情况,以第1颗卫星的星下点位置为参考,分别统计了距离星下点轨迹±0.5°、±0.5°～±1°、±1.0°～±1.5°、±1.5°～±2.5°、≥±2.5°共5个不同区域单历元TDOA定位误差,结果统计见表2。

表2 距离星下点不同区域定位误差(针对单历元)

由表2可知,尽管星下点轨迹附近部分点位定位误差偏大,但定位误差均值相对总均值降低并不显著,表明该三星编队构型总体定位性能有保障。

综上可知,无论是低纬区域还是中纬区域,在波束覆盖范围内,卫星星下点轨迹附近信号源定位精度相对最差,但精度较差区域占比小于13%。究其原因与仿真编队卫星构型有关。为保证三星编队运行稳定型,减少轨控次数,本次仿真采用了类似鹰眼360高低搭配的编队卫星构型,该构型中3颗编队卫星基本分布在近似同一轨道面内,星下点轨迹周边点相对3颗卫星定位几何构型差(近似位于同一平面),表现为TDOA定位观测方程近似线性相关,导致星下点轨迹附近信号源定位误差相对较大。通过对波束覆盖范围内全部点定位误差进行统计,80%以上点定位误差小于510 m。有高程信息约束时,三星编队单历元定位理论残差为零,受非线性方程迭代计算方法和计算机数值有效位影响,实际残差有微小变化。

2.3 3颗卫星多历元定位结果

尽管有地面高程信息支持条件下,3颗卫星单历元TDOA观测数据可确定信号源位置,但该方法适用性一般,仅适用于海面或大范围地形平坦地区,地形复杂地区先验高程信息很难获取。考虑到监视卫星短期内可实现对地面特定信号源的连续测量,可获取多个历元数据,多个历元TDOA观测量同样可解决单历元测量秩亏问题。为此,本文开展了三星编队多历元TDOA定位仿真试验。

多历元TDOA定位试验采用的仿真编队卫星构型、仿真数据生成策略和地面点选择区域与单历元类似,区别是单次定位计算利用了2 s采样间隔连续20 s数据,同时考虑到卫星运动对多历元测量信号波束重叠覆盖范围的影响,对比单历元星下点选择区域,本文将多历元地面信号源格网点范围缩小为星下点周边半径450 km范围。考虑地球自转影响条件下,仿真3颗监视卫星对每个格网点间隔2 s连续20 s距离差观测量,利用20 s TDOA数据确定信号源位置,将定位结果与理论值比较,统计位置误差与误差分布,结果如图6—图9所示。

图7 多历元中纬区定位误差等值线Fig.7 Geolocation errors contour of medium latitude for multi-epoch

图8 多历元低纬区定位误差Fig.8 Distribution of geolocation errors of low latitude for multi-epoch

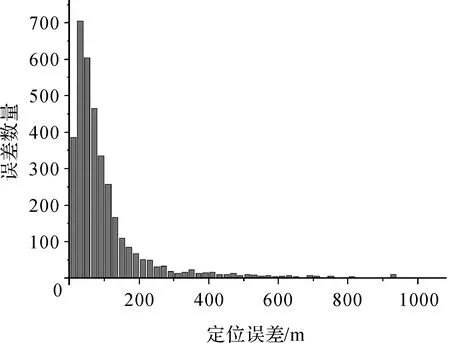
图9 多历元中纬区定位误差Fig.9 Distribution of geolocation errors of medium latitude for multi-epoch

与单历元定位类似,本文分别统计了编队卫星星下点轨迹周边5个不同区域多历元TDOA定位误差,结果见表3。

表3 距离星下点不同区域定位误差统计(针对多历元)

与单历元定位类似,多历元定位同样存在沿星下点轨迹方向定位误差偏大问题,但定位误差增大点位数量和与幅度总体可控。同时与单历元定位相比,多历元总体定位精度显著改善,平均定位误差提高到110 m。相比文献[6]的定位结果有显著提高。

影响多历元定位精度的因素还包括采样间隔和多历元累积处理弧长。处理弧长选择主要受信号重叠覆盖范围限制。采用多历元定位时,由于卫星运动,卫星可接收信号的波束覆盖范围不断发生变化,导致多历元共同可观测范围的重叠覆盖区域相对减小。采样间隔不变时,累积处理弧长越长,累加计算的历元数越多,尽管定位精度相应有改善,但多历元共同覆盖区域也将越小。因此,累积处理弧长选择需要平衡定位精度和共同覆盖区域影响。

对于运行速度相近的卫星,处理弧长可用弧段时长表征。为分析处理弧长对定位精度影响,采用1 s采样间隔,分别进行了累加处理弧长为5、10、15、20、25 s时多历元定位仿真试验,精度统计结果如图10所示。

图10 处理弧长与定位精度关系Fig.10 Geolocation accuracy with processing arc lengths

由图10可知,增加多历元累积处理弧长,能够有效提高多历元定位精度,当累加处理弧长取为20 s时,定位精度提升效率已不显著。因此,本文将本次仿真条件下多历元累积处理弧长选为20 s。

当多历元累积处理弧长确定后,累积处理历元个数主要取决于数据采样间隔。TDOA观测最小采样间隔受积分时长限制,由式(2)可知,积分时长T直接影响TDOA测距精度,因此,为保证一定测距精度,单次测量数据采样间隔不能过小。为分析累积处理历元个数对定位精度影响,采用本节多历元定位仿真条件进行了仿真定位试验。仿真采用的多历元累加处理弧长选择为20 s,分别选取采样间隔为5、2、1、0.5、0.25、0.1 s、进行了多历元定位试验,与上述采样间隔对应的累积处理历元数分别为4、10、20、40、80、200。多历元定位结果与历元数关系如图11所示。

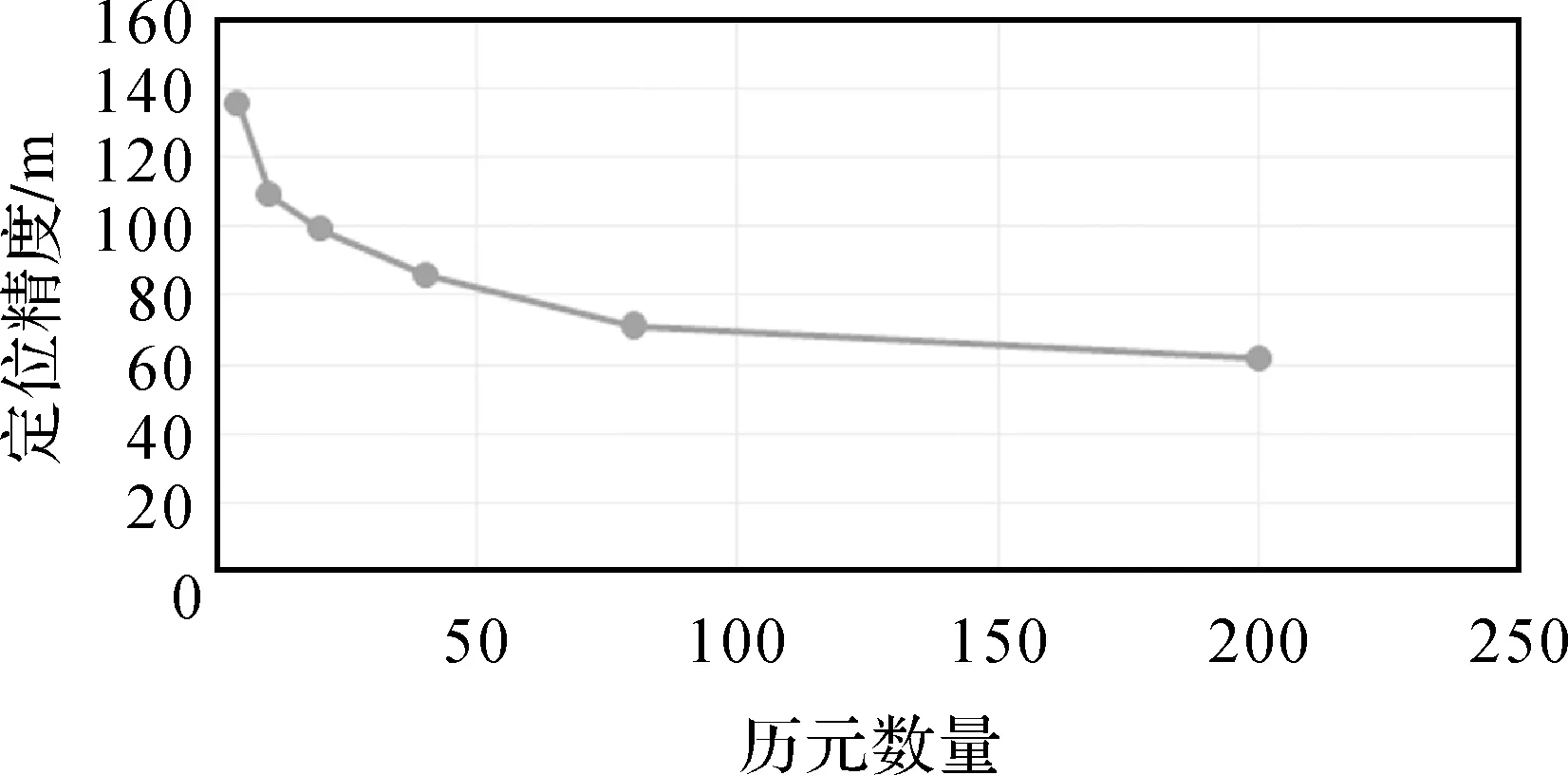
图11 历元数与定位精度关系 Fig.11 Geolocation accuracy with the number of observation

由图11可知,当累加处理弧长不变时,数据采样间隔减小,处理历元个数增加有助于提高定位精度。但采样间隔减小受多种因素制约。首先,最小采样间隔受测量精度制约;其次,星基TDOA定位通常采用星载处理模式,测量历元数的增加意味着星间数据传输量和星载处理能力要求的同步提高,同时弱信号观测通常需要用多次测量通过数据平滑消减随机噪声和粗差,经过平滑后有效数据采样间隔不可能太低,因此,综合平衡多种因素影响,确定数据采样间隔选择1～2 s相对合理。

3 结 论

采用天基卫星监测信号源是目前国内外热点研究方向,基于TDOA方法信号源位置测定技术是其中关键技术。本文研究了三星编队单历元及多历元TDOA定位方法,利用仿真数据分析了其可能实现的信号源位置确定精度。初步仿真结果表明,三星编队监测卫星单历元信号源定位误差在510 m量级,而多历元定位误差可降低到110 m量级。编队构型对信号源定位误差分布有直接影响。本文主要针对地面静态信号源定位,对于动态如何实现多历元定位,还需要结合FDOA观测量开展进一步研究工作。