Effects of strain on the flat band in twisted bilayer graphene

Zhen Zhang(张镇), Lu Wen(文露), Youkai Qiao(乔友凯), and Zhiqiang Li(李志强)

College of Physics,Sichuan University,Chengdu 610064,China

Keywords: graphene,moir´e superlattice,magic angle and strain

1.Introduction

Many correlated and topological electronic phases have been discovered in twisted bilayer graphene (TBG) in recent studies,[1-19]which has led to an outburst of research based on this system over the past few years.[20-23]These novel quantum states originate from the formation of flat electronic bands near a magic twisted angle (～1°) under the influence of the moir´e superlattice.[20-37]Such flat bands exhibit a sensitive dependence on small lattice deformations[24,38]that are induced by lattice relaxation or strain.On the other hand, strain is an effective tool for engineering the flat bands[24,39]and thus helps us understand the various exotic quantum states in TBG.

Previous experimental[8]and theoretical works[24,36,39-41]have shown that applying a heterostrain (relative strains between layers) in a two-layer structure can significantly modify the band structures and electronic phases.Due to the interaction between substrate and graphene in the preparation process, various strains are prevalent in actual TBG samples.Therefore,it is of great significance to study the effect of different types of strain on the flat bands in TBG.The influence of uniaxial heterostrain on the bands of TBG has been explored in detail in previous studies.[24,38,42,43]However, there are few detailed studies[39,44]on the difference and connection between the effects of various types of strains on the electronic structure of TBG.

In this paper, we systematically investigate the effect of different heterostrains on the moir´e band structures and density of states (DOS) of TBG based on a low-energy effective continuum model.We show that various strains strongly affect the band structures of TBG near the magic angle.Compared with the twisted angle,only a small magnitude of strain is required to cause separation between the conduction band and the valence band.Volume-preserving strain can broaden the van Hove singularities compared with shear strain, and both types of strain have dissimilar dependence on strain direction.In addition,unlike other strains,the effect of biaxial strain on TBG is very similar to that of the twisted angle both geometrically and electronically.Therefore,certain angles that are difficult to achieve during sample fabrication experimentally can be replaced by applying biaxial strain.The effects of dissimilar strains on the band structures and DOS have very subtle differences, which can be used to experimentally distinguish various types of strain.Our findings regarding the flat bands and van Hove singularities have broad implications for the novel quantum phases in TBG,which can be directly studied by scanning tunnelling microscopy(STM)experiments.[6-8,17]

2.Theoretical background

For TBG without strain, where the two graphene layers are only rotated relative to each other, the moir´e superlattice forms an array of equilateral triangular domains with alternating AB and BA stacking regions.However,the moir´e pattern and the corresponding Brillouin zone of TBG are significantly distorted in the presence of heterostrain.An example of the associated moir´e pattern generated with various strains is shown in Fig.1.Because the moir´e superlattice period is much larger than the atomic scale in the limit of the small twisted angle,the continuum model can efficiently capture low-energy electronic structures,[20,29,45]which allows us to analyze the effect of geometrical deformation (including the twisted angle and strain)on the physical properties of TBG.

Here the antisymmetric part,labeled byT(θ),represents a rotation matrix with twisted angleθ.The symmetric part, labeled byS(∊), represents the strain with magnitude ∊.Obviously, the shape of the unit cell as well as the Brillouin zone are both geometrically affected by deformationE.Therefore,the rescaled primitive and reciprocal lattice vectors can be expressed as[24]

HereAiandGi(i=1,2)refer to the primitive vectors and the reciprocal vectors without deformation,respectively.

For a TBG system,a periodic variation of the layer stacking order can emerge with a small value of deformationE,as shown in Fig.1.In our calculation,we consider a TBG system starting with AA stacking and then apply various geometrical deformationsE.Hence, the reciprocal lattice vectorsgiand the primitive lattice vectorsaiof the moir´e superlattice[24]are

respectively.Here,E=E2-E1is the relative deformation matrix between two layers of graphene,whereEl(l=1,2)represents the deformation acting on each single layer of graphene.In this paper, the respective deformation of each layer is regarded asE1=-E2=E/2, that is, the two graphene layers are rotated and strained oppositely with the same magnitude.

Based on the effective continuum model,the Hamiltonian of TBG can be written as

whereUis the interlayer coupling of two graphene layers andhl(l=1,2)is the intralayer Hamiltonian of layerl, which is given by the two-dimensional gapless Dirac equation[24]

In Eq.(5),ξ=±labels theK(K＇)valley andσx(σy)is the Pauli matrix in the sublattice space.In the following calculations, we take ¯hvF/a ≈2.1354 eV.[25]Within a simple twocenter approximation and the small-strain limit, the position of the Dirac fermionDl,ξin momentum space is[24]

with

whereKl,ξdenotes the location of theK(K＇)valley for layerlandAis the strain-induced vector potential.[24,46]In theAterm,the hopping modulus factor isβ ≈3.14[46]and ∊xx(∊yy,∊xy) represents the component of the two-dimensional strain tensor.

Moreover, the effective interlayer couplingUis given by[20,24]

whereω= e2πi/3anduandu＇are the amplitudes of the diagonal and off-diagonal terms in the sublattice space,respectively.[47]They reflect the influence of lattice ripples on the moir´e band structures.In particular, in the smalldeformation regime,competition between the interlayer interaction and the elastic energy at the interface can lead to significant lattice relaxation for TBG.The reconstruction can be taken into account by usingu=0.0797 eV andu＇=0.0975 eV in our calculation,which are the interlayer coupling strengths of AA/BB and AB/BA stacked regions,respectively.[33,47]

In the following, we introduce into the effective Hamiltonian four different types of strain that are common in two-dimensional materials, namely, shear strainSsh, volumepreserving strainSvp,biaxial strainSbaand uniaxial strainSua.In Fig.1,we display the corresponding moir´e pattern and the moir´e Brillouin zone under various strains with magnitude∊=0.7% for TBG near the magic angle (θ=1.05°).Four general forms of strain have been derived in detail in previous reports.[24,44]In addition, to further understand the effect of strain direction on the electronic band structures of TBG,we consider an angleφof strain relative to the A1 axis(fouraxis coordinate system)in our system.[8]Therefore,the strain tensor can be modified to the following form:[24,44]

The above four strains are characterized by the strain magnitude ∊and the directionφ.Here, the parameterν=0.16 is the Poisson ratio[8]for graphene.Then,the deformation matrixEcontaining the strain directionφand magnitude ∊is obtained for TBG,and is of the formE=S(∊φ)+T(θ).

3.Results and discussion

Based on the effective continuum model described above, we calculate the electronic band structures of TBG at a fixed twisted angleθ=1.05°close to the magic angle under four different types of strain.In this article,the path of band structures is along the linek1→γ→k2→M→γ→M→k1in the moir´e Brillouin zone scheme,as shown by the red dashed line in Fig.1(a).In addition,we also perform a series of controls on the electronic band structures by varying the strain magnitude ∊and directionφ.These results are fully displayed and discussed in this section.

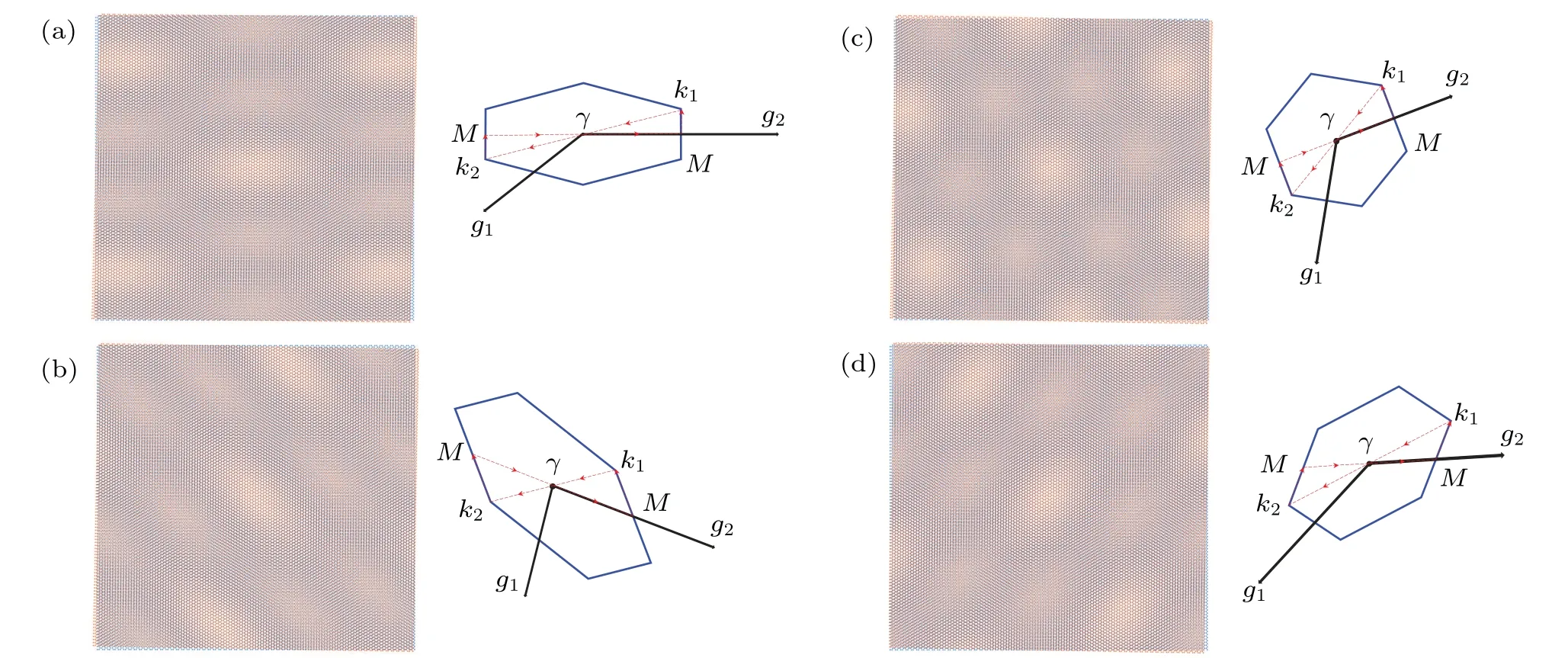
Fig.1.Schematic representation of the moir´e pattern and moir´e Brillouin zone for TBG with a twisted angle θ =1.05° under the influence of four types of uniform strain along the armchair direction,namely,(a)shear strain,(b)volume-preserving strain,(c)biaxial strain and(d)uniaxial strain.The parameters of these strains are magnitude ∊=0.7%and direction φ =0°.The red dashed line in(a)represents the momentum path for the energy band plots.

3.1.Shear strain

Interlayer and interfacial shear strain play crucial roles in the performance and application of TBG.However, the key parameters controlling shear strain have been poorly studied both experimentally and theoretically.Note that the form of shear strain considered in Eq.(9) is similar to that in the research of Koshinoet al.,[39]and our form is equivalent to that in Ref.[39] under certain conditions.In particular, the shear strain form we considered is of more universal and practical significance, and can be combined with experimental studies.[48-51]

In Fig.2, we show the band structures and DOS of the TBG system under shear strain with various magnitudes ∊and directionsφ.When the strain magnitude ∊=0,TBG exhibits flat bands with vanishing band velocity near the charge neutral point (CNP), resulting from competition between the kinetic energy and the interlayer hybridization energy.Correspondingly,as shown by the black line in Figs.2(a)and 2(b),the DOS has a strong peak near the CNP.However, the flat bands near the CNP are very sensitive to variation of the strain magnitude ∊,and even a small magnitude of ∊=0.1%causes them to split significantly, as shown in Figs.2(a) and 2(b).Moreover, as the magnitude ∊of strain increases, the energy separation of the lowest conduction band and valence band increases systematically.Then, the corresponding peaks in the DOS also shift systematically to higher energies with increase in ∊.Unlike flat band features, the remote bands are slightly affected by the strain magnitude ∊.Although the energy gap between the flat bands and the higher-energy bands becomes smaller with increase in ∊,the two are not connected and still maintain a small energy gap ofΔ～0.24 meV.Moreover,the energy shift of the two flat bands mainly occurs at theγpoint,and the band dispersion is also mainly distributed near theγpoint.The two bands are quite flat in most other regions of the Brillouin zone.In particular,shear strain does not open the gap near the CNP due to the symmetry ofC2zT,and the conduction band and valence band are still connected by a Dirac crossing point.Because the threefold rotational symmetries are broken by the strain,the two Dirac crossing points are no longer located at the corners of the Brillouin zone but at a generic point.[24,38]

Compared with the strain magnitude ∊, the electronic band structures of TBG are almost insensitive to the strain directionφ,as shown in Fig.2(c).This is because the behavior of the flat band is highly correlated with the asymmetric and anisotropic components of the strain tensor.[39]However, the structure of van Hove singularities changes subtly with various strain directionsφ.It can be clearly observed from Figs.2(a)and 2(b)that the DOS shows one or two smooth main peaks atφ=30°and 9°,while the prominent peaks of the DOS exhibit some shoulders and the van Hove singularities are broadened when the directionφdeviates by 30°or 90°.In addition, the system is periodic forφ →φ+π/3 originating from the symmetry of the unstrained system.Thus, the DOS of TBG with shear strain also goes through periodic changes.

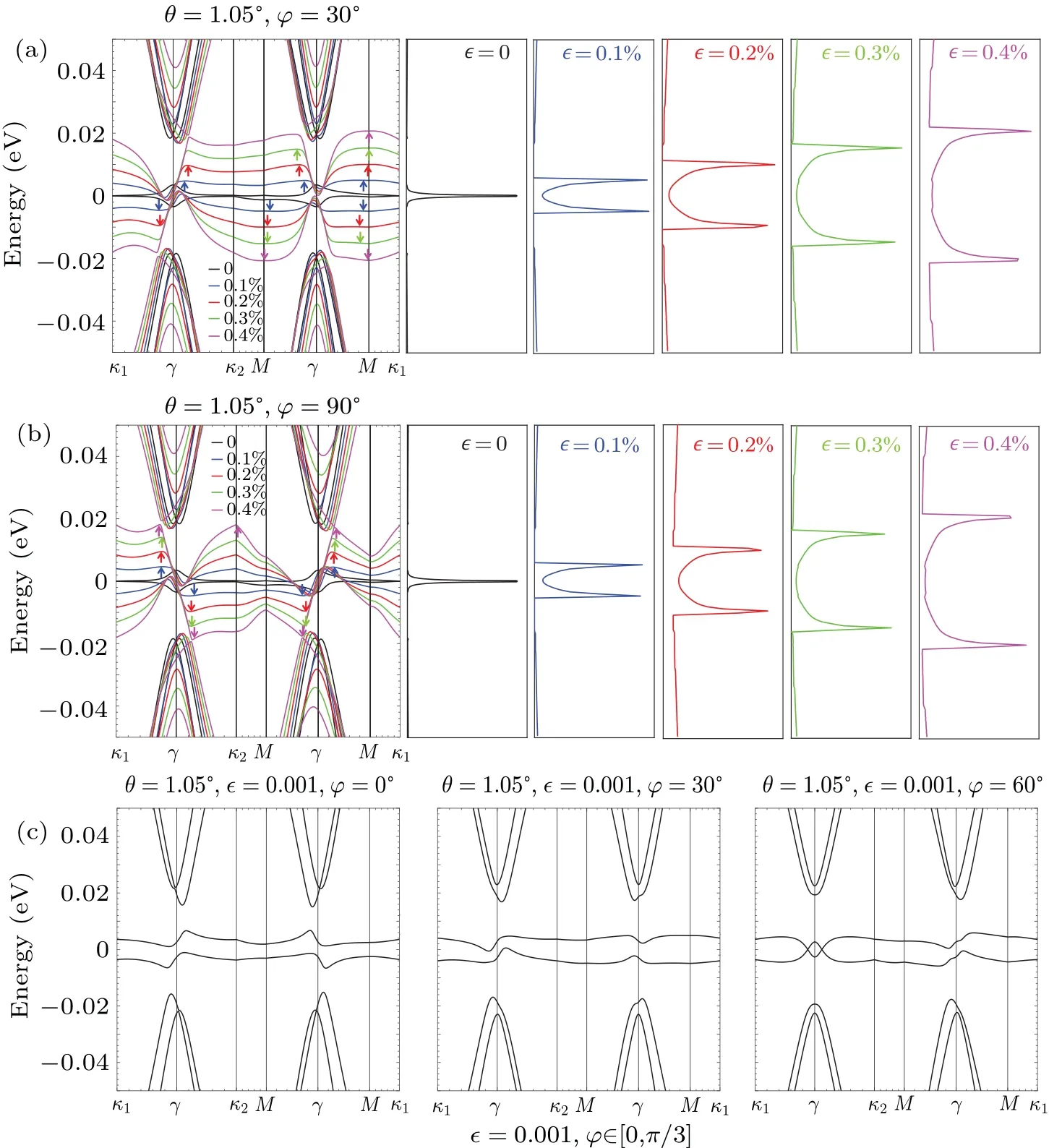
Fig.2.Band structures and the DOS of magic angle TBG considering the shear strain.(a)Strain direction φ=30°and magnitude ∊=0,0.1%,0.2%,0.3%,0.4%.(b)Strain direction φ=90°and magnitude ∊=0,0.1%,0.2%,0.3%,0.4%.Different colors represent different magnitudes of strain.The colored arrows mark the energy corresponding to the van Hove singularities.(c)The band structures of different directions φ with the strain magnitude ∊=0.1%.

3.2.Volume-preserving strain

Volume-preserving strain is another heterostrain that is relatively common in two-dimensional systems.[24]The specific forms of volume-preserving strainSvpare listed in Section 2.According to Eq.(10),the materials are strained with a magnitude of ∊along the directionφand a magnitude of-∊along the vertical directionφsimultaneously.

The effect of strainSvpfor a series of strain magnitudes on the electronic structures of TBG atφ=30°andφ=60°is shown in Fig.3.Under the action of volume-preserving strain,the variation of the flat band with magnitude ∊is similar to that of the shear strain,as illustrated in the band structures in Figs.2(a),2(b)and 3.However,compared with the results for shear strain,the DOS in Fig.3 demonstrates the unique influence of volume-preserving strain on the TBG system.When the increasing parameter ∊is taken into account,the characteristic peaks in the DOS are significantly broadened while moving to higher energies.In addition,the prominent peaks in the DOS evolve from a single peak to a group of peaks consisting of multiple secondary peaks at ∊＞0.2%.Moreover, at the same magnitude ∊,the shape of the two peak groups changes with strain directionφ,which is most obvious when ∊=0.4%.

Fig.3.Band structures and the DOS of magic angle TBG considering volume-preserving strain.(a)Strain direction φ =60° and magnitude∊=0, 0.1%, 0.2%, 0.3%, 0.4%.(b) Strain direction φ =90° and magnitude ∊=0, 0.1%, 0.2%, 0.3%, 0.4%.Different colors represent different magnitudes of strain.The colored arrows mark the energy corresponding to the van Hove singularities.

3.3.Biaxial strain

Biaxial strain is a kind of strain in which a lowdimensional system is subjected to stress in both arbitrary and perpendicular directions.In general, biaxial strain is only related to the magnitude ∊and is independent of the strain directionφ,as derived from Eq.(11).

Figure 4(a) shows the influence of biaxial strain on the electronic structures in TBG under different strain magnitudes∊.Unlike shear strain and volume-preserving strain, biaxial strain does not open the band gap of TBG at thek1point.As shown in Fig.4(c), since the threefold rotational symmetry is not broken when biaxial strain is applied to TBG, the two Dirac crossing points connecting the two energy bands are always located at the corners of the Brillouin zone.Biaxial strain can greatly affect the behavior of the lowest conduction band and the valence band,whereas the remote bands are independent of the strain magnitudes ∊.Besides, with increase in ∊,the energy gaps between the two flat bands near the CNP and the remote bands decrease gradually and tend to overlap.In Fig.4(b), we show the electronic band diagram of TBG with an additional small rotation angle Δθaround the magic angleθ ≈1.05°.It can be observed that the effect of twisted angle Δθon electron structures is very similar to that of biaxial strain in TBG.This finding can be attributed to the biaxial strain-induced vector potentialA=0, resulting in geometrical biaxial strain effects consistent with the twisted angle.Our results are agreement with previous studies on TBG under biaxial strain.[44]

3.4.Uniaxial strain

Uniaxial strain is a kind of strain in which the bilayer system is subjected to relative stress in one direction but not in the vertical direction.In previous studies,[52,53]uniaxial strain was found to exist extensively in TBG samples.The influence of uniaxial strain on the electronic band structure of TBG has been described in detail in previous works,[17,24,38,42,43]and the most important feature caused by uniaxial strain is the energy separation between the conduction band and the valence band near the CNP.

3.5.Discussion

We have described in detail the characteristics of the band structures in the TBG system under the influence of various strains.Next, we discuss the connections and differences between the dissimilar strains.We can clearly observe that the central flat band of TBG is very sensitive to all strains.Each strain near the magic angle broadens the bandwidth of the central flat band, leading the large energy separation of van Hove singularities in the DOS.These behaviors can be directly observed in STM experiments.[6,8]It is found that shear strain and volume-preserving strain have similar effects on the electronic structure of TBG,because asymmetric heterostrainsE1=-E2=E/2 are taken into account in our calculations.The central flat band splitting of TBG is mainly related to the anisotropic normal componentand the shear component ∊xyof the strain tensor, which has been explained in previous work by using the pseudo Landau level picture of TBG.[39]

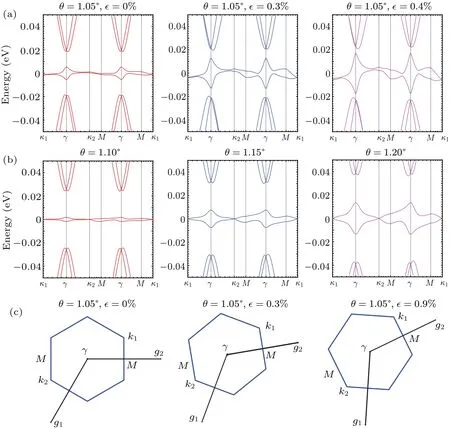
Fig.4.Band structures of TBG with different (a) biaxial strain magnitudes ∊=0.1%, 0.3%, 0.4% and (b) twisted angles θ =1.10°, 1.15°,1.20°.Different colors represent different magnitudes of strain and twisted angle.(c)The moir´e Brillouin zone of TBG under various biaxial strain magnitudes ∊.

We also analyze the differences between the dissimilar strains.Firstly, we find that the bands under different strains have different dispersion.Compared with shear strain, the structure of the van Hove singularity of TBG under volumepreserving strain has broader peaks in the DOS.Secondly,biaxial strain has a very unusual effect on the band of TBG compared with the other three types of strain.Biaxial strain does not break the threefold rotational symmetry of the TBG lattice.The changes in the band and DOS of TBG under the influence of biaxial strain are very similar to the effect of twisted angle.In fact,the geometric effect of biaxial strain is similar to that of twisted angle,as shown in previous studies.[44]Finally,unlike the complete separation of the central flat bands under uniaxial strain,shear strain and volume-preserving strain cause the flat band to change dramatically near theγpoint,such that under certain conditions the central flat bands intersect at locations other than the intersection of the two Dirac points.This result means that the electronic and optical behavior of the two flat bands can no longer be considered from the perspective of isolated bands.

4.Conclusion and perspectives

In this paper, we systematically studied the electronic band structure and DOS of magic angle TBG with different types of strain based on the effective continuum model.We find that the flat band near the CNP is greatly sensitive to shear,volume-preserving and uniaxial strain,which leads to distinct behaviors in the flat bands and DOS.Unlike uniaxial strain,the energy transition of shear strain and volume-preserving strain is more intense near theγpoint of the central flat band, and the two types of strain have dissimilar strain direction dependences, which enables us to extract a lot of critical information about band structure.In addition, biaxial strain is unusual compared with the other strain modes in that the effect on TBG is very similar to that of the twisted angle both geometrically and electronically,which provides a way to achieve some twisted angles that are difficult to fabricate experimentally using biaxial strain in the future.Finally, we found that different types of strain lead to corresponding characteristic peaks and thus modify the van Hove singularities in the DOS of the flat bands,which are expected to significantly influence the correlated and topological electronic phases in TBG and can be studied by future STM experiments.[6-8,17]

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant No.11874271).We thank Yan He for theoretical support and discussions.