Large valley Nernst effect in twisted multilayer graphene systems

Guanlin Jian(简冠林), Zhen-Gang Zhu(朱振刚)2,3,,†, and Gang Su(苏刚)4,,3,‡

1School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

2School of Electronic,Electrical and Communication Engineering,University of Chinese Academy of Sciences,Beijing 100049,China

3CAS Center for Excellence in Topological Quantum Computation,University of Chinese Academy of Sciences,Beijing 100190,China

4Kavli Institute for Theoretical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

Keywords: valley Nernst effect,twisted multilayer graphene

1.Introduction

Thermoelectric power generation(TPG)is a powerful and ecological technique to generate electricity from waste or environmental heat by directly converting thermal energy to electric energy without any mechanical and chemical mediations.The conventional way of TPG is to utilize the Seebeck effect,which is a longitudinal effect describing an establishing electric field parallel to the applied temperature gradient.However,it is still a challenge to improve the dimensionless figure of meritZTfor getting a high energy conversion efficiency.On the other hand, a different pathway to realize high efficiency of the TPG via the anomalous Nernst effect has been emerging.[1,2]Compared to the Seebeck-effect-based TPG,the Nernst-effect-based TPG has a few advantages.Firstly,it can be applied to large size heat sources by making lateral thermopiles rather than the perpendicular thermopiles for the Seebeck-effect-based TPG.Secondly, the thermoelectric conversion for the Nernst-effect-based TPG can be related to the thermal conductivity (κxx) and electric conductivity (σyy)which are along or perpendicular to the temperature gradient(assume to be inxdirection),respectively.It is well known that the Seebeck-effect-based TPG involves thermal conductivity(κxx)and electric conductivity(σxx)which are both along the direction of temperature gradient.However,the Wiedemann-Franz law tells us thatκxx/σxx=LT, whereLis the Lorentz number.Thus, the thermal conductivity and electric conductivity may not be tuned independently in the Seebeck-effectbased TPG.But they are not suffered the regulation from the Wiedemann-Franz law in the Nernst-effect-based TPG, because they are not in the same direction.This may provide us an extra freedom to tune the performance of the corresponding devices.[3]Therefore, this Nernst-effect-based TPG has great potential applications.The present challenge is that the Nernst coefficient is small in usual materials.For example,it is about 1µV/K for FePt with a high uniaxial magnetic anisotropy.[4]This value is quite small so that it may not be used in realistic applications easily.Since the anomalous Nernst effect is closely determined by Berry curvature of Bloch bands in momentum space for its intrinsic mechanism,a higher Nernst coefficient may be achieved in materials with nontrivial topological properties.Recently, valley Nernst effect (VNE) has been proposed in monolayer group-VI dichalcogenides[5]and tested in experiment.[6]The VNE describes that charges from each valley make contribution to the anomalous Nernst coefficient due to nonvanishing Berry curvature in the valley.In the presence of time-reversal symmetry, different valleys possess opposite Berry curvatures leading to Nernst currents in the opposite directions.Therefore,the total Nernst coefficient from the two valleys is zero.If the valley degeneracy can be lifted,for example by straining the entire system, only one valley participates in the Nernst current,a nonzero total Nernst coefficient can be measured due to the single-valley-contribution which is a few orders of magnitude larger than that in NiFe in experiment.[6]Therefore, the VNE exhibits great potential in TPG.This inspires us to seek for materials with even larger valley Nernst coefficient.We will show that the VNE is enhanced dramatically in twisted multilayer graphene(TMG).

Twisted bilayer graphene (TBG) has attracted much attention after the observation of the correlated insulating phases[7-11]and unconventional superconductivity.[9,12,13]The low-energy physics of twisted graphene systems are characterized by flat bands[14,15]around the “magic angles”.The magic angle systems extend fast from TBG to twisted trilayer graphene,[16-21]twisted double bilayer graphene[22-27]and twisted multilayer graphene[28,29]in theoretical and experimental aspects.Experimentally,many strong correlated physics including Mott insulator,unconventional superconductivity, nematicity,[30-34]strange metal,[35,36]and ferromagnetism[8,37-41]were found in twisted bilayer graphene.[42-46]Theoretically, many low-energy effective models, such as tight-binding model,[28,47-51]effective Wannier tight-binding model,[52-59]density functional model,[60-62]and effective continuum model[14,15,63,64]were proposed to describe generic TBG systems.Based on these models, many theories have been proposed to calculate the property of twisted graphene systems and mainly to figure out the electronic structures,[16,55-58,65-70]the strong correlated phases[41,42,46,70-82]and the mechanism of unconventional superconductivity.[63,75,77,78,80,83-88]

In addition, topology, which is currently one of the key topics in condensed physics, also finds its importance in twisted electronics.Experimentally, the observation of hysteresis loops and chiral edge current of the TBG,[43]and more importantly, the observation of well-quantized resistance of the hBN-aligned TBG[39,43]demonstrates the existence of quantized anomalous Hall (QAH) state,[41,89]the topological phase, in twisted electronics.Theoretically, it was shown that the four low energy flat bands of twisted bilayer graphene have nontrivial topology,[69,90]more accurately the fragile topology,[24,58,69]because of their odd windings of Wilson loops.[65,78,91]The nontrivial topology of twisted bilayer graphene[92]is believed to originate from the equivalence between the four flat bands and the zeroth pseudo-Landau level with opposite Chern numbers and sublattice polarizations.[78,93]Also in TMG withN-layer graphene being placed with a twisted angle onM-layer graphene as shown in Fig.1, two low energy flat bands for each valley exist.Moreover,Chern-number hierarchy in the(M+N)-layer TMG system was found.[29]The quantum valley Hall effect, orbital magnetism,and anomalous Hall effect[34,43]are believed to exist in the TMG.Furthermore, the valleytronics in twodimensional materials based on manipulating the valley index is of great importance.[94-99]Motivated by these works,we study the anomalous valley Nernst effect of(M+N)-layer TMG systems.We find that the anomalous valley Nernst coefficient shows interesting and rich features with layer numbers,chirality,and temperature,especially for the flat bands.

2.Model and method

We study the(M+N)-layer TMG with theM-layer chirally stacked (the ABC stacking) graphene being placed on top of the otherN-layer chirally stacked graphene.And theM-layer part is twisted by a nonvanishing angleθwith the otherN-layer part,as schematically shown in Fig.1(a)(for the case ofM=2,N=2).The twisted angle obeys a relation cosθ(m)=(3m2+3m+1/2)/(3m2+3m+1),[29]wheremis a positive integer.In the TMG system, the unit cell for untwisted systems becomes now a moir´e supercell for moir´e superlattice so that the Brillouin zone(BZ)of the moir´e supercell has been significantly reduced compared with those of the untwisted multilayers,as shown in Fig.1(d).We study a model that describes the behavior of the system at the first magic angle of TBGθ=1.05°.[29]Specifically,from the perspective of the pseudo-Landau levels,in a multilayer system with chirality,almost flat pseudo-Landau levels of opposite Chern numbers will be generated.The two flat bands are pinned to zero energy and remain almost flat even after being coupled with other layers in the TMG systems as long as the chiral symmetry is preserved.[29,68]On this basis, we can construct the Hamiltonian by dividing the(M+N)-layer TMG system into three subsystems with the TBG as the interface of TMG, the(M-1) layers below the TBG, and the (N-1) layers above the TBG, as schematically shown in Fig.1(c).Here we consider theKvalley(Fig.1(d))only,and the effective Hamiltonian atK＇valley can be obtained by applying a time reversal operation to that at theKvalley.

We take a part of the system(three-layer graphene)shown in Fig.1(e) as an example to explain the charality.The +stacking chirality means that theB1sublattice of the upper layer is strongly coupled with theA2sublattice of the middle layer,forming pairs of bounding and antibounding states.And theB2sublattice of the middle layer is strongly coupled with theA3sublattice of the lower layer.For the schematic threelayer case in Fig.1(e),theA1sublattice of the upper layer and theB3sublattice of the lower layer are left as two low-energy degrees of freedom.Similarly,the-stacking chirality has the reversedAandBsublattice of the upper and lower layers as the two low-energy degrees of freedom.Thus,the low-energy effective Hamiltonian of the (M-1)-layer graphene around theKvalley can be obtained by(M-1)-th order perturbation theory,[100]which gives

wheret⊥is the interlayer hopping within the (M-1)-layer part andα=±is the stacking chirality associated with theMlayers.

The low-energy effective degrees of freedom of the TBG at the interface around theKvalley are two flat bands which are pinned to zero energy.So the corresponding low-energy effective Hamiltonian reads

whereε1(k)=ε2(k)=0.

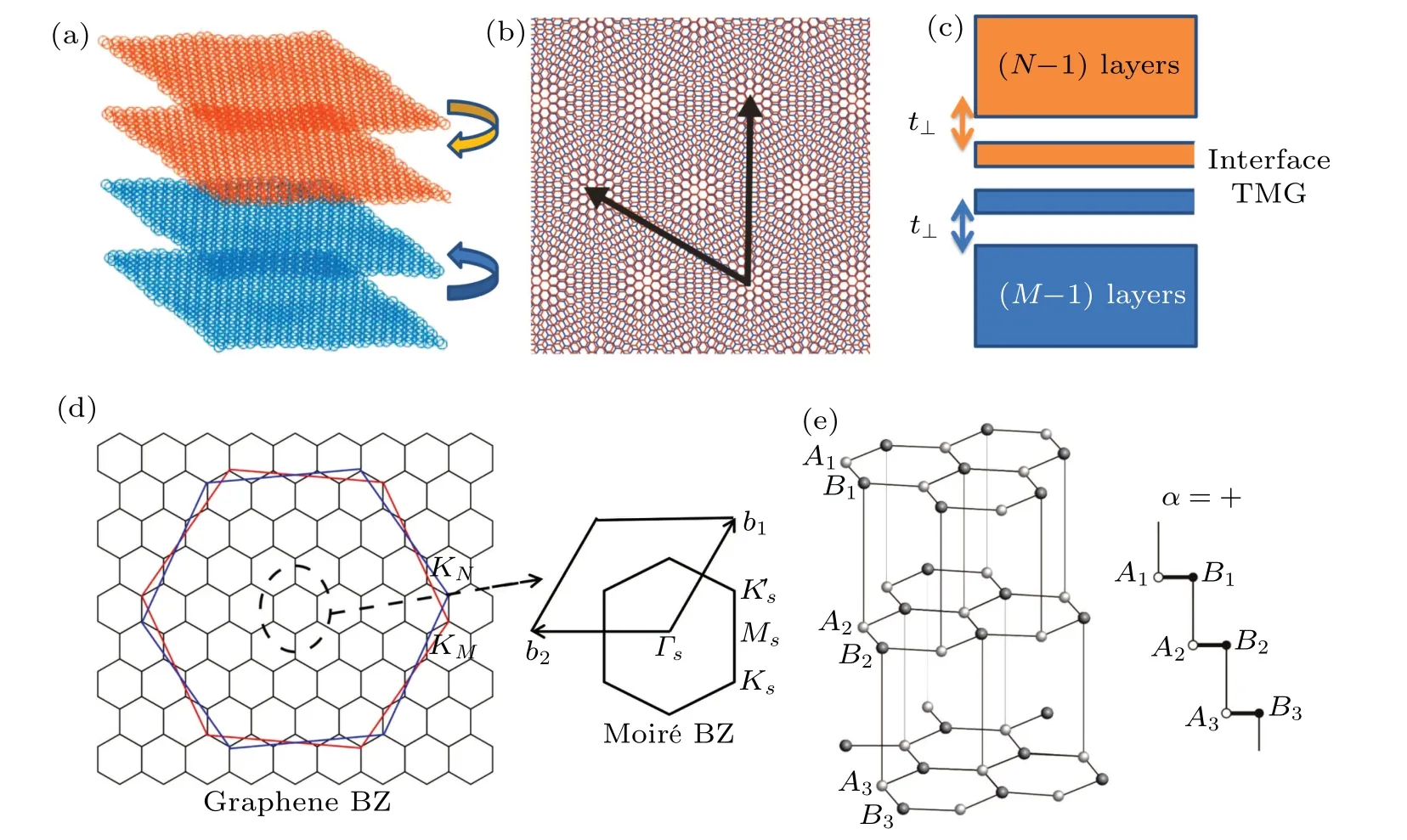
Fig.1.(a) Structure of the twisted multilayer graphene with M =2 and N =2.(b) Moir´e pattern of the twisted multilayer graphene, seen from the top.The two black arrows denote the lattice vectors of the moir´e supercell.(c)A schematic illustration of the TMG system.(d)The Brillouin zones of the top N multilayers,bottom M multilayers,and the moir´e supercell are plotted in red,blue,and black lines,respectively.KN and K＇N are top N multiplayers graphene valleys. KM and K＇M are bottom M multilayers graphene valleys.[29] (e)The ABC stacking with“+”chirality in graphene multilayers.The vertical lines are coupling between different layers.In“+”stacking chirality sublattices B1A2 and B2A3 are strongly coupled leaving A1 and B3 as two low-energy degrees of freedom.The“-”stacking chirality is obtained when reversing the sublattices A and B in the above sequence.This means for“-”stacking chirality sublattices A1B2,A2B3 are strongly coupled leaving B1 and A3 as two low-energy degrees of freedom.

Now we consider the coupling between the flat bands of the TBG and the (M-1)-layer part.If the stacking chirality is+as that in Fig.1(e),the degree of freedom from theAsublattice(for example theA1)of the upper-most atomic layer of the(M-1)-layer part is coupled to one of the two flat bands.After including this coupling between(M-1)-layer part and the flat bands from the interface TBG, the low-energy effective Hamiltonian around the moir´eKspoint (contributed by theM-layer part)is now

wherehαis the effective coupling with

andh-=.Hereteffis the low-energy effective coupling parameter between the states of the (M-1)-layer graphene and the flat bands from the interface TBG.Inserting Eqs.(1),(2), and (4) into Eq.(3), we obtain the low-energy effective Hamiltonian around the moir´eKspoint

where

Similarly, the low-energy effective Hamiltonian around the moir´eK＇spoint is

whereα＇=±is the stacking chirality of theNlayers andmN-1is given by Eq.(6).Here we should point out that the twisted angleθdoesn’t enter into the Hamiltonian directly.It gives rise to redefinition of the momentum in the first BZ from the moir´e supercell.The moir´e effects in these equations are embodied in the two flat bands.The interlayer coupling parameterteffbasically contains the effect of the twisted angle.However we treat it as a fitting parameter and the entire study is valid at the first magic angle,i.e.,θ=1.05°.We can solve Eqs.(5)and(7)analytically.The eigenenergies of Eq.(5)are expressed as

The eigenenergies of Eq.(7)have the same expression but with(M-1) replaced by (N-1).The eigenstates ofHαKs(k) are expressed as

Similarly,for the low-energy effective Hamiltonian around the moir´eK＇spoint described by Eq.(7), the Berry curvatures of conduction band (subscript index 1), flat band (subscript index 2)and valence band(subscript index 3)are derived as

When a temperature gradient is applied, an electric field develops in the opposite direction because of the Seebeck effect.Besides the parallel effect, in the presence of the temperature gradient,the electrons experience a Lorentz-like force and thus move in the direction perpendicular to the diffusion current, which is the anomalous Nernst coefficient effect (ANE)induced by the intrinsic nonvanishing Berry curvature.This is also the intrinsic mechanism contributing to the anomalous Hall resistivity.[101,102]Thus,the velocity multiplied by the entropy density gives rise to the anomalous Nernst coefficient(ANC)[5]around moir´eKsand moir´eK＇spoints

wheren=1,2,3 represent the conduction band,flat band,and valence band, respectively.β0=(ekB/2h),eis the electron charge,his the Planck constant,SnM(k)=-fnMklnfnMk-(1-fnMk)ln(1-fnMk)(Boltzmann constantkBhas been absorbed inβ0) is the entropy density for moir´eKspoint andn-band, andfnMkis the Fermi distribution function.The entropy density develops a peak when the eigenenergies match the chemical potentialsµ,and is essentially zero when the energy is beyond the range of [µ-5kBT,µ+5kBT].The integration is performed over the neighborhood of moir´eKs(K＇s)point in the momentum space.ΩnM(k) andSnM(k) can be expressed as functions of the modulus of the wave vectork.For the flat bands,we make the integration in the entire moir´e Brillioun zone:

wherektakes values in the entire moir´e Brillioun zone.For the conduction and valence bands, we can use the Debye model,[103,104]namely, the integration is taken in a circular region centered at moir´eKs(K＇s) point and the area is equal to the half of the first moir´e Brillouin zone for moir´eKs(K＇s)point.Thus,Eq.(13)can be written as

For brevity,we callβM(βN)the one moir´e point VNC.

The total VNC is composed of the contributions of all crystals,i.e.,βT=βM+βN,we have

The total flat band VNC is given byso we have

The VNC from the conduction and valence bands is then

For brevity,we callβCVas the conduction-valence band VNC.

3.Results and analysis

The magnitude of the VNE is determined by the VNC.In the following,we investigate the properties of the VNC for the valleyKfor a freestanding layer.Corresponding to the valleyK, there is a full first moir´e Brillouin zone with moir´eKsand moir´eK＇spoints around where the energy bands are corresponding to upNlayers and downMlayers in our chosen model.For each moir´eKs(K＇s)point there are three bands,the conduction band, flat band and valence band.All six bands VNC should be considered since the valence band, the conduction band, and the flat bands are close to the Fermi level,and may all contribute to the VNC.Specifically, we calculate the total VNCβT,βFand the conduction-valence band VNCβCVto clearly reveal their contributions respectively.In our calculation, parameters are taken as follows: the interlayer hopping in the (M-1) layerst⊥=0.001 eV, the lowenergy effective coupling between the states of the (M-1)layers and the flat bandsteff= 0.01 eV, the Fermi velocityυF=1016°A/s,graphene lattice constanta=2.46 °A,the Boltzmann constantkB=0.8629×10-4eV/K,and the Plank constant ¯h=0.6582×10-15eV·s.

In Fig.2, we show howβT,βFandβCVvary with TMG layers at the temperature of 300 K.The layer number(M+N)changes from 4 to 9,corresponding toM=2,N=2;M=2,N=3;M=3,N=3;M=3,N=4;M=4,N=4;andM=4,N=5.We take theM-layer chiralityα=1 and theN-layer chiralityα＇=-1 in all these conditions.In the following discussion,the chirality condition will keep the same.If the sign of chirality is changed, the sign of VNC will be changed but the value keeps the same.In Fig.2(c), we find that the value of the total VNC (βT) for TMG at least can reach-66.19β0(the peak value of 2+2 TMG) that is three orders of magnitude larger than that of MoS2which is 0.14β0[5,104]at room temperature.The large value ofβTfor TMG is expected because two low-energy bands in the TMG system possess valley Chern numbers that are dependent on both the number of layers and the stacking chiralities.[29]From Fig.2,it is observed that the absolute value of the total VNCβT,the total flat VNCβFand the conduction-valence VNCβCVall increase with the increase of the layer number.βCVis positive; whileβFtakes negative values.The total flat VNCβFand the conductionvalence VNCβCVincrease much faster than that of the total VNCβT.The increase of VNC by stacking more layers can be understood simply as the Berry curvature is also increased.Although the stacked more layers are not adjacent to the interface TBG,they are effectively coupled to the interface TBG via the layers in-between these stacked more layers and the interface TBG.However, this intuitively simple scenario may not be extended to an infinite-layer system since the VNC cannot be increased to infinity.This indicates that there is a limitation on the studied model that may not be applicable to the cases of very largeMandN.For the very largeM+Ncase, the situation becomes very complicated and is beyond our study.This can be left for further explorations.The observations of VNC shown in Fig.2 are consistent with the valley Chern numbers of TMG derived in Ref.[29]in which the valley Chern numbers increase with the increase of the layer number.This means one can enhance the valley Nernst effect by simply increasing the thickness of the TMG.

The(M+N)-layer TMG systems are divided into theMlayer part and theN-layer part, so we have different layernumber combinations corresponding to different systems for a fixed total layer number.For example,total 5-layer TMG systems have two different situations:M=3,N=2 andM=2,N=3.In Fig.3, we show the variation of the total VNCβTwith respect toµ.Two features can be summarized in the following.Firstly,if we only exchange the layer numberMand the layer numberN,the total VNC keeps the same.For example, the total VNC of the system withM=3,N=2(M=4,N=3)is exactly the same as that of the system withM=2,N=3(M=3,N=4).Secondly,for the same total number of layers,when the difference betweenMandNis larger,the total VNC absolute value becomes slightly larger.For example,as seen in Fig.3(d),the total VNC of the system withM=3,N=5(orM=5,N=3)is a little larger than that of the system withM=4,N=4; while the total VNC of the system withM=2,N=6 (orM=6,N=2) is larger than that of the system withM=3,N=5(orM=5,N=3).But generally,Fig.3 shows that different lines nearly overlap with each other, which means with the fixed total layer number, the total VNC of the system with differentM-layer part andN-layer part are nearly the same.The results are roughly consistent with Ref.[29]in which the valley Chern numbers are fixed by the total layer number.

Now let us investigate the properties of VNC relating to the temperature.To be more specific, we calculate the oneflat band VNCβM2(see Eq.(13))and the one-conduction band VNCβM1around moir´eKsof the TMG system withM=2.Figure 4(a)displays the broadening of the peak ofβM2around zero Fermi energy at higher temperature.It is interesting to note that the maximum value ofβM2does not change with temperature.In Fig.4(b),the one-conduction band VNCβM1has a similar broadening of the peak, but its maximum value increases with increasing temperature.This different property of maximum values between flat band and the one-conduction band results from the fact that the Fermi distribution functionfnMk=0.5 is independent of temperature for flat band because whenµ=ε2k=0 we have(µ-ε2k)/T=0.

We have discussed the behavior of the VNC at relatively high temperature.We should emphasize that the relatively high temperature induces a mixing contribution of different bands to the VNC.It is possible to distinguish their single role in the VNC at relatively low temperature.Figure 5 shows the low temperature VNCβMin Eq.(16) around one moir´e pointKs.TheβMis composed of three contributions: conduction band,flat band and valence band.The main feature is the three-peak structure where a main peak is around at the center (aroundµ= 0) with negative value, and two shoulder peaks with positive values locate at a higher and a lower Fermi energy.We should point out that the central peak is induced by the flat band,and the right(left)peak stems from the conduction (valence) band.Because the flat band VNC and the conduction (valence) band VNC have opposite signs, the magnitude of the central peak (the total VNC) is slightly decreased with increasing temperature.Thus at sufficiently low temperature,the central peak and shoulder peaks are separated completely because of the gap between the flat band and conduction(valence)band.

Fig.5.The VNC βM in Eq.(16)around moir´e point Ks as a function of the Fermi energy with different low temperatures.

In the following,we want to estimate the critical temperature below which the three-peak structure can almost fully be distinct.In Fig.5,the temperature is 30 K,and the three-peak structure can only be distinguished approximately.It is known that the entropy density is essentially zero when the energy is beyond the range of [µ-5kBT,µ+5kBT].[5]So when the range of 10kBTis smaller than the energy gap (in our model the energy gap equals toteff), the contribution from different bands to the one moir´e point VNC can be clearly separated.Therefore,by 10kBT=teff=0.01 eV,we estimate this critical temperature to be 11.63 K below which the three peaks can be fully separated and the predicted feature in this work can be more easily tested.

4.Summary and discussion

In this paper, we have studied the valley Nernst coefficient (VNC) of (M+N)-layer TMG systems and found that the total VNC is three orders of magnitude larger than that in monolayer group-VI dichalcogenides.We should emphasize that there are many ways of multilayer graphene stacking leading to different systems, for example, trilayers in which one of the three layers is twisted by a small angle relative to perfect AAA,ABA,or ABC stacking,[105]the three-layer configurations corresponding to a twisted monolayer on a bilayer of graphene,the four-layer configurations including a twisted monolayer on a trilayer,and a twisted bilayer on a bilayer and so on.[106]Different stacking leads to different systems with different properties.Our study is only applicable to gaped systems, specifically for the system we described.To know clearly the behavior of the VNC,we take into account the contributions from moir´e pointsKsandK＇s,and three energy bands(i.e.,the conduction,flat and valence bands).We find that the total VNC is quite huge,which is at least three orders of magnitude larger than that for two-dimensional MoS2-like materials.The reason might be that the energy gap of TMG is much smaller than that of MoS2-like materials which gives rise to much larger Berry curvature for TMG.It is found that the total, flat-band, and conduction-valence band VNC all increase with increasing layer number.Here we have to point out that when layer number (M+N) is large enough then we can not regard the present TMG as a two-dimensional system.When stacking more layers,the coupling between these extra layers and the twisted layers is reasonably assumed to be smaller and smaller.In this case, the twisted effect on the VNC may be decreasing.Thus, our conclusions may only be applicable to the systems with finite layers.

At sufficiently low temperature, the contributions from the conduction, flat and valence bands can be clearly separated, manifesting a larger total VNC because of lacking offset.These results are expected to be tested in near future experiments.This work presents a huge valley Nernst effect in TMG systems,which would have potential applications in designing novel thermoelectric devices.

Acknowledgements

Project supported in part by the National Key R&D Program of China(Grant No.2018YFA0305800)and the National Natural Science Foundation of China (Grant Nos.11974348 and 11834014).It is also supported by the Strategic Priority Research Program of Chinese Academy of Sciences(Grant Nos.XDB28000000 and XDB33000000).ZGZ is supported in part by the Training Program of Major Research plan of the National Natural Science Foundation of China (Grant No.92165105)and CAS Project for Young Scientists in Basic Research(Grant No.YSBR-057).