Influence of viscous force on the dynamic process of micro-sphere in optical tweezers
Jing Liu(刘静), Xingyu Wu(吴星宇), Yimin Feng(冯怡敏), Mian Zheng(郑冕), and Zhiyuan Li(李志远)
1College of Computer Science,South-Central Minzu University,Wuhan 430074,China
2China Ship Development and Design Center,Wuhan 430064,China
3School of Physics and Optoelectronics,South China University of Technology,Guangzhou 510640,China
Keywords: optical tweezers,viscous force,equations of Newtonian mechanics,Runge-Kutta method
1.Introduction
The advent of optical tweezers has greatly promoted progress in the measurement of the forces and observation of the dynamics at the single molecule level,leading to a greater understanding of biochemical processes.[1]However, in the nano-world, ordinary water behaves as a very viscous liquid.The particle moving in water is like moving in the syrup.Viscosity consumes a lot of energy, which leads to a decrease in the momentum exchange and transfer between light and objects.Unlike levitating particles in liquid, optical trapping of nanoparticles in vacuum[2-4]is isolated from environmental thermal noise,thus eliminating the primary source of dissipation, which has attracted great attention in fundamental tests of quantum mechanics,[5,6]sensing of weak forces,[7,8]and searching for new physics.[9,10]In contrast to optical trapping in fluid surroundings,optical trapping in gaseous surroundings is quite challenging because of the high particle velocities and the low drag forces.
On the other hand,the optical tweezer technique has been developed to manipulate particles with light absorption, such as metallic nanoparticles[11-14]and metallic-dielectric Janus microparticles.Different from the trap of dielectric material, these materials give rise to strong heating effects.It has been reported that nanoparticles can rotate at frequencies of several kilohertz when trapped in the circularly polarized light.[15]Due to the loss of materials and the thermal effect caused by light absorption,the surrounding waters will generate thermal[1]convection.The heating of the particles at high laser powers facilitates optical spinning because it lowers the viscosity and friction of the embedding water.Note that the common law of viscosity applies to most fluids,but there exist some materials that exhibit anomalous viscous properties.Anomalous properties may be conferred on a fluid by small particles immersed in it.[16]The viscosity of the nanofluid suspension with the same material nanoparticles varies with the particle size.Heet al.[17]found that the viscosity of TiO2-distilled water nanofluids decreases with the miniaturization of the micro-sphere size.
Measuring real-time dynamics is crucial for uncovering the distinct mechanics of a micro-sphere.Research on the motion of an optically trapped Brownian particle has aroused great interest due to the applications of a sensitive probe of molecular and nanoscopic forces.Both experimental and numerical simulations research on an optically trapped particle have made progress,[18-20]but research on the effects of the viscous coefficients of the surrounding medium on microparticles is insufficient.In this paper, we focus on the influence of viscous coefficients on the micro-spheres in optical tweezers.First,we numerically analyze the three-dimensional(3D)dynamic process of dielectric micro-spheres in optical tweezers on the basis of the equations of Newtown mechanics.Second,we display the trajectories of the motion of micro-spheres when they are in the surrounding medium with different viscosity coefficients.Moreover, due to the different oscillation frequencies of optical tweezers along thex- andz-axes, we have considered the dynamics of the micro-sphere when it is set at different initial positions.Finally, we have reported that the equilibrium time mainly depends on the corresponding damping coefficient of the surrounding environment and oscillation frequency of the optical tweezers.
2.Optical force on the micro-sphere in optical tweezers
In optical tweezers, any particle falling within the laser beam undergoes two kinds of forces:a restoring force directed toward the region of highest intensity (gradient force) and a force that pushes the particle along the propagation axis of the laser beam (radiation pressure).A 3D stable trapping condition is achieved when the field gradient force overcomes the radiation pressure,the forces due to gravity and buoyancy,and the force animating the Brownian motion.If the particle is not far from the trap center,the optical force exerted on the particle is directly proportional to the displacementrfrom the equilibrium position.Since an optical trap behaves, with a good approximation, like a harmonic potential, it is able to exert a restoring force,Foptical=κ·r, whereκis the trap stiffness.Normally in an optical trap the radial optical forces are larger than those of the axial one, i.e.,κx ≈κy >κz.A schematic of the optical tweezers considered in this work is shown in Fig.1(a).
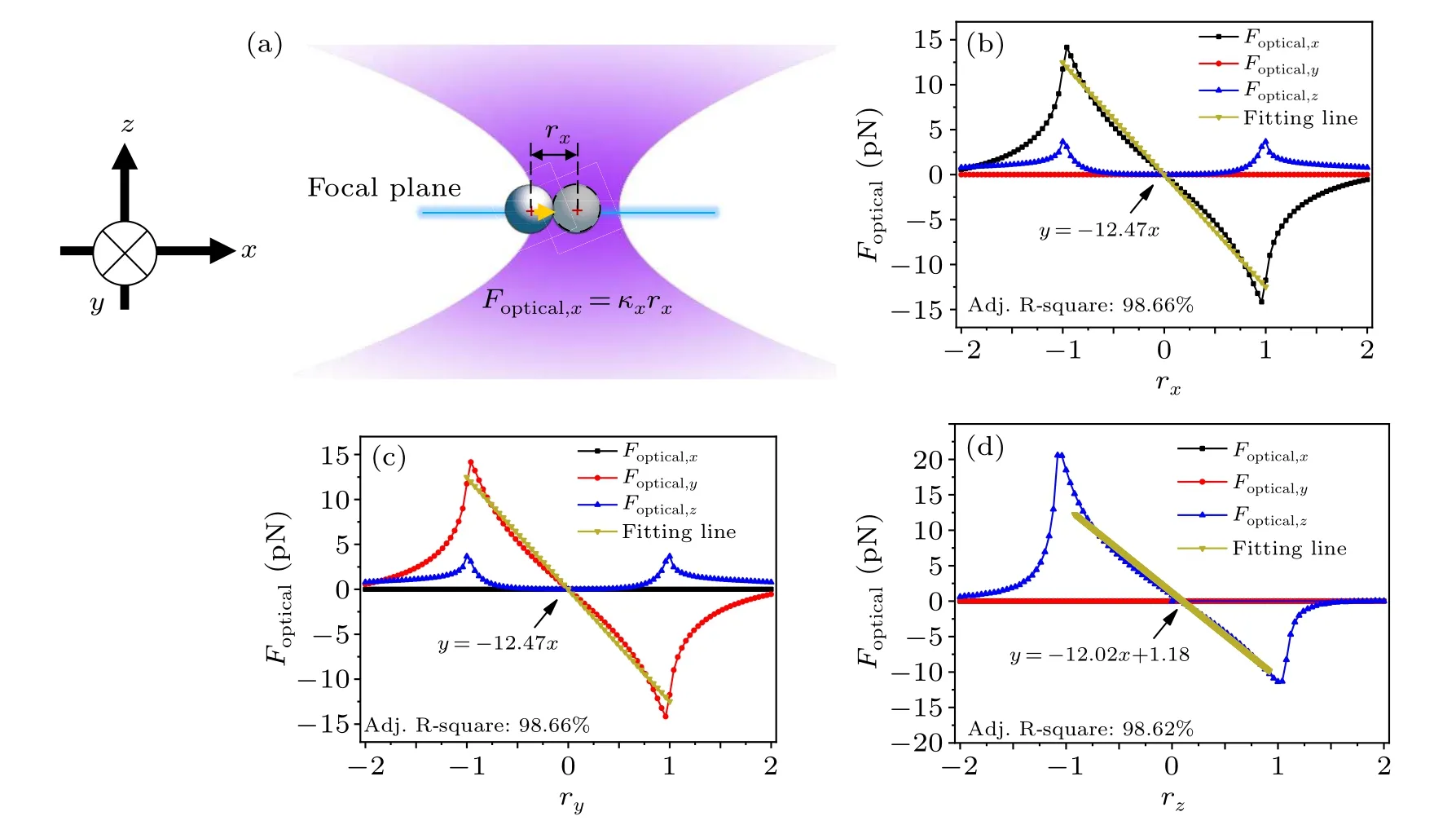
Fig.1.(a)Schematic of optical tweezers and the coordinate system.(b)-(d)The calculated optical force acting on a micro-sphere when it moves along the x-,y-and z-axes,respectively,in the optical tweezers at the laser power P=10 mW.
The collimated Gaussian beam at a wavelengthλ=1064 nm propagates along thez-axis and is focused by a high numerical aperture (NA=1.4) objective.We implement the ray optics model and algorithm in Ref.[21]to calculate the optical force (Foptical=[Foptical,x,Foptical,y,Foptical,z]) of a dielectric micro-sphere in an optical tweezer when the micro-sphere with radiusrsmoves around the focus point along thex-,y-,andz-axes, respectively.In the ray optics model, the focused Gaussian light beam is decomposed into a large number of individual rays.The rays are reflected and refracted at the interface of the particle and the surrounding medium.The optical force at each point quantitatively can be calculated via the principle of the exchange of momentum.The initial parameters are as follows.The surrounding medium is water with a refractive indexn1=1.33,the dielectric micro-sphere has a refractive index ofn2=1.6 and radiusrs=1µm,and the laser power isP=10 mW.In Figs.1(b)-1(d),we display the calculated optical forces as a function of the position along thex-,y- andz-axes of the micro-sphere around the identified equilibrium position.Here,the two most important features of optical tweezers are shown: the maximum axial force and spring constants that characterize the strength of the trap.Through linear fitting of the data in the Hookean region, the trap stiffness coefficients inx-,y- andz-axes are calculated and they areκx=κy=-12.47 pN·µm-1andκz=-12.02 pN·µm-1,respectively.The trap stiffness is fitted by the yellow line in the corresponding figure.Through calculating the optical force exerted on the micro-sphere,the equilibrium position of the micro-sphererequilibrium=[0,0,0.085] µm in the optical tweezers.
3.Equations of motion of the micro-sphere
In the optical tweezers, based on the equations of Newtown mechanics, the trapped micro-sphere motion can be approximated by
whereris the particle position in 3D space andmis the mass of the micro-sphere,4.36×10-15kg.
The drag force acting on the particle can be written as
whereγis the viscous drag coefficient.For a spherical bead,γis expressed by the Stokes equation,γ=6πηrs, whereηis the fluid viscosity, 0.89×10-3Pa·s for water, and 1.81×10-5Pa·s for air at room temperature.[22]
The gravitational forceGand buoyancy forceFbuoyacting on the micro-sphere are expressed as
whereρsandρwcharacterize the density of the microsphere and water, respectively.Since the direction of gravity and buoyancy is along thez-axis, their resultant forces pass through the center of mass and do not provide torque to the micro-sphere.Here,Vsis the volume of the micro-sphere andgis the acceleration of gravity.
The Brownian motion of micro-spheres is mainly the irregular motion caused by the uninterrupted impact of environmental molecules on the micro-spheres and can be expressed by[23]
wherekBis the Boltzmann constant, andTis the temperature of the surrounding environment.In addition, Δt=t(i+1)-t(i) is a finite time interval, andN(0,1) denotes a Gaussian variable with zero mean and variance equal to 1.Brownian force is a random force due to collisions with the solvent molecules.The force cannot be determined and can only be described by a probabilistic method.According to Ref.[23], the mean-squared displacement〈(Δrx)2〉 is 3.4×10-4µm2whenη=0.89×10-3Pa·s by performing Brownian dynamics simulations when the stiffness coefficientκx=-12.47 pN·µm-1.
The motion of the trapped micro-sphere in viscous liquid can be modeled as a forced damped oscillator.In this case,the trapped micro-sphere oscillates in the viscous liquid.The motion of the laser trap is treated as an optical force applied to the micro-sphere,while the drag force in the viscous liquid corresponds to the dampening of oscillations.In this case,owing to the asymmetry of the optical focus, the oscillation frequenciesalong the three main axes are different(ωx=ωy=53.47 kHz,ωz=52.51 kHz).The corresponding damping coefficientβcan be given byβ=γ/(2m).And then the dynamic differential equation of the micro-sphere by rewriting Eq.(1)as
This is the differential equation for free oscillations with viscous damping.Several points may be noted about the solution of the equation.The function of which was differentiated twice to obtain the above equation may have contained two arbitrary constants that disappeared in the differentiation.The general solution must then contain two arbitrary constants that are to be evaluated with the use of the boundary conditions.
The solution must represent a vibration with a continually decreasing amplitude if the damping is not too great.If the damping is very great,the particle should return to its equilibrium position with decreasing velocity and no vibrations will take place.There should be a borderline case when oscillations just cease and the particle returns to its equilibrium position in a minimum time.
There are clearly three situations,namely,
(i)β2>ω2i,overdamping;
(ii)β2=ω2i,critical damping;
(iii)β2<ω2i,underdamping.We shall consider these cases separately in the above order.
4.Method of the differential equation (the fourth-order Runge-Kutta method)
Since Eq.(5) cannot be solved analytically, we consider using the Runge-Kutta method to numerically analyze this equation.[24]Runge-Kutta is an important class of implicit or explicit iterative methods for the solution of nonlinear ordinary differential equations (ODEs).It combines classical methods such as the Euler algorithm and trapezoidal,and has the characteristics of high precision,which is very suitable for the situation in this paper.One of the above methods is very commonly used and is called the fourth-order Runge-Kutta method (RK4 method).It is mainly applied in the case of computer simulations when the derivatives and initial value information of the equation are known.This method eliminates the complex process of solving differential equations and has been successfully used to solve ODEs.The second-order differential Eq.(5) can be converted to two coupled first-order equations
The time step Δtshould be much smaller than the characteristic time scales of the stochastic process to be simulated.If the Δtis comparable to or larger than the smallest time scale, the numerical solution will not converge and typically shows an unphysical oscillatory behavior or divergence.The characteristic timescale of our entire model is given by the relaxation timem/γ, so the minimum relaxation time is about~27 ns.In our calculations, we set the time step to 10 ns,such thatδt <m/γ.The recursive algorithm for the classical RK4 method can be written as follows:
The velocity and position of the micro-sphere during the next integration time interval can be obtained from the following equation:
With the fourth-order Runge-Kutta method,we can accurately calculate the kinetic parameters of the micro-sphere in the optical capture.
5.Results and analysis
The time reversal properties of a dynamical law signal are its dissipative character.To probe oscillations in the liquiddamped regime,a feasible route is to reduce the viscosity coefficient.For better illustration of the above three situations presented in Section 3, we display the trajectories of the motion of the micro-sphere when it is in the surrounding medium with different viscosity coefficients.Due to the different oscillation frequencies along three main axes,we have considered the trajectories of the motion of the micro-sphere when it is set at different initial positions.
5.1.Micro-sphere set on the z-axis
The initial parameters are listed as follows: the initial positionr0=[0,0,1]µm and the velocityv0=[0,0,0]µm·s-1In terms of thez-axial oscillation frequencyωz=52.51 kHz,when the fluid viscosity isη=2.43×10-5Pa·s the microsphere undergoes critical damping along thez-axis.Due to the symmetrical structure of optical tweezers and micro-spheres,the micro-sphere is forced by thez-axis optical force, and moves along thez-axis.Figure 2 shows the temporal evolution of thez-trajectories of a micro-sphere in liquids with different viscosities,η=0.89×10-3Pa·s,0.89×10-4Pa·s,2.43×10-5Pa·s, 0.89×10-5Pa·s, and 0.89×10-6Pa·s.The corresponding dynamic motions of micro-spheres with different viscosities are shown in the supplementary materials video S1.Table 1 displays the damping coefficient, oscillation frequency, and the equilibrium time and state of the micro-sphere with different viscosities in the optical tweezers.Whenη= 0.89×10-3Pa·s or 0.89×10-4Pa·s, because of the large damping and sufficient cushion, the whole system has enough capacity to dissipate energy.The microsphere will not oscillate back and forth, but will tend to balance monotonously and slowly in the overdamped oscillation.Finally, it respectively takes 1.05×10-2s and 1.98×10-3s to reach the equilibrium positionrequilibrium=[0,0,0.085]µm.Whenη=0.89×10-5Pa·s or 0.89×10-6Pa·s, in terms of the small damping and slow dissipation, the restoring force pulls the micro-sphere back to the equilibrium position but rushes over the position, making several periodic oscillations back and forth.With the increase of time, the whole system dissipates the kinetic energy of the micro-sphere,which causes that the amplitude of the oscillation of the micro-sphere to become smaller and smaller.In these cases,it respectively takes 6.09×10-4s and 5.05×10-3s to reach the equilibrium position.Whenη=2.43×10-5Pa·s, this situation lies between the above two situations.And the whole system has the minimum ability to prevent oscillation.In this situation, it takes 3.44×10-4s to return to the equilibrium position.Therefore,it can be concluded that,in the critical damping oscillation,it takes the least amount of time for the micro-sphere to reach the equilibrium state.

Fig.2.The z-directional trajectories of the micro-sphere with different viscosity coefficients, and η =0.89×10-3, 0.89×10-4, 2.43×10-5,0.89×10-5,and 0.89×10-6 Pa·s at the initial position r0=[0,0,1]µm and the velocity v0=[0,0,0]µm·s-1 in the optical tweezers.

Table 1.The relevant physical parameters of the micro-sphere with different viscosity coefficients when the micro-sphere is set at the initial position r0=[0,0,1]µm.
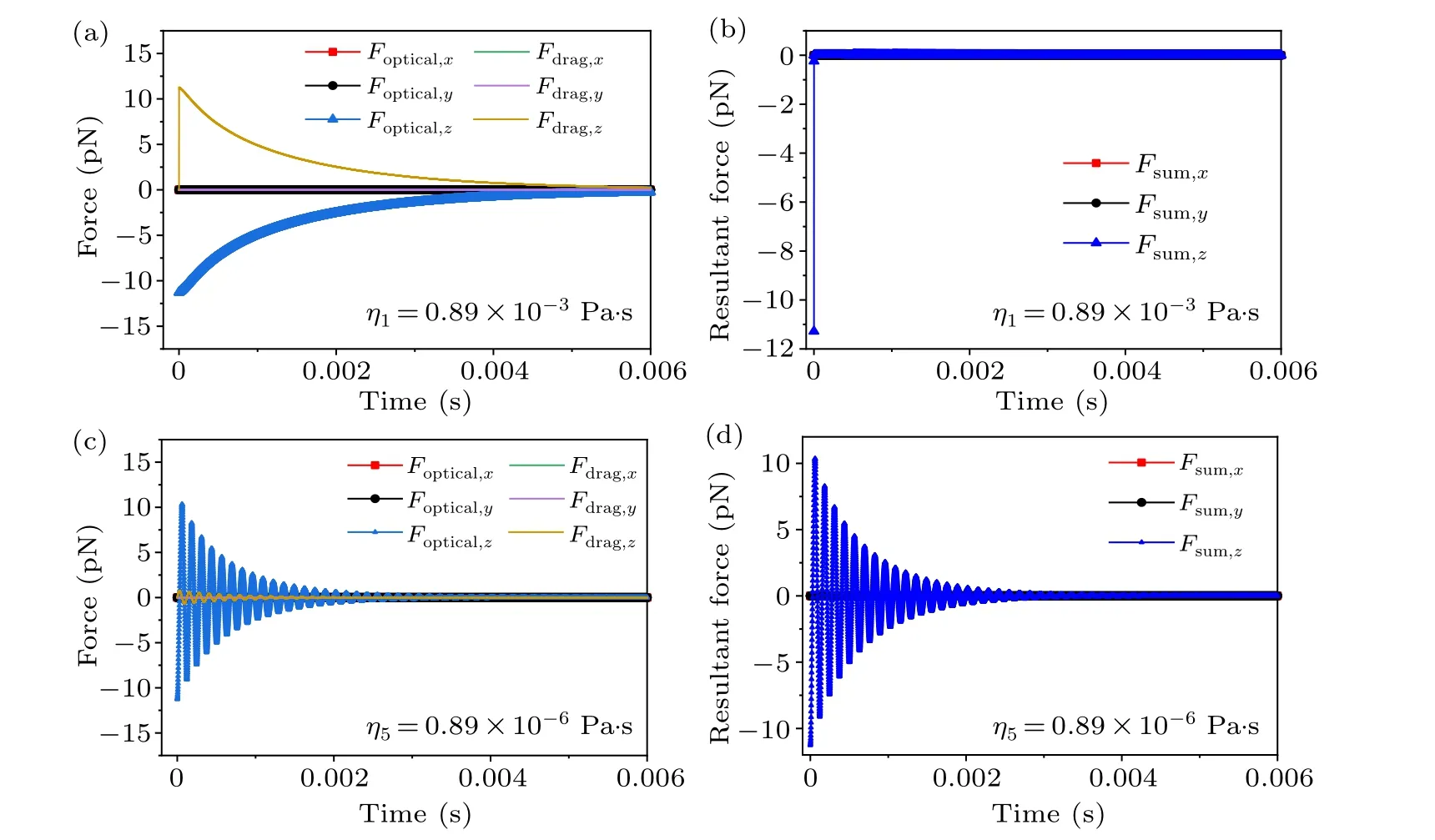
Fig.3.The temporal evolution of the x-, y-, and z-directional [(a), (c)] optical force and drag force, [(b), (d)] resultant force of the microsphere with viscosity coefficients η1 =0.89×10-3 Pa·s and η5 =0.89×10-6 Pa·s at the initial position r0 =[0,0,1] µm and the velocity v0=[0,0,0]µm·s-1 in the optical tweezers,respectively.
For clear illustration,we plot detailed pictures of the optical force,the viscous drag force,and the resultant forceFsum(Fsum=Foptical+Fdrag+G+Fbuoy, which are the same in all contexts) of the micro-sphere with viscosity coefficientsη1=0.89×10-3Pa·s andη5=0.89×10-6Pa·s in Fig.3.As shown in Figs.3(a)and 3(b),at the initial stage,the initial velocity of particle is zero.The drag force is zero too,but the optical force is very large(11.28 pN at 10 mW),and so is the resultant force.As a result,the particle is subject to a very large acceleration to raise its speed up to the maximal velocity in a short time.However,the drag force grows quickly along with the speed of the particle to the extent that it completely compensates for the optical force and makes the total force zero.This transition happens at a small timescale of only 2.18µs at 10 mW.After this time,the drag force overwhelms the optical force because the latter decays faster,leading to a negative net force consequent deceleration of the particle until it reaches the translational equilibrium position.In Figs.3(c) and 3(d),due to the viscosity coefficientη5=0.89×10-6Pa·s,the optical force far outweighs the drag force.The resultant force mainly depends on the optical force,decreasing with the dissipation of the particle kinetic energy.At this stage,the particle is like a mechanical spring,oscillating back and forth in line,as shown in Fig.2.It takes about 3 ms at 10 mW in this reciprocating process to slowly reach the balance state.
5.2.The micro-sphere set on the x-axis or y-axis
In the following case,we consider the oscillation frequencies of the micro-sphere along thex-axis, which is similar to the situation along they-axis.The initial position of the microspherer0=[1,0,0.085]µm,the velocityv0=[0,0,0]µm·s-1,and the oscillation frequencies in thexandyaxes areωx=ωy= 53.47 kHz.Different from the first case, the microsphere experiences thex- andz-optical forces in the optical trap.The micro-sphere does not translate directly to the equilibrium position.Instead, it moves in a complex curve.Thex- andz-trajectories of the micro-spheres in the different viscosity liquids as a function of time are displayed in Figs.4(a)and 4(b).To better illustrate the state of the motion the particle, the corresponding optical force, the viscous drag force,and the resultant force of the micro-sphere with viscosity coefficientsη1=0.89×10-3Pa·s andη5=0.89×10-6Pa·s are shown in Figs.4(c)-4(f).When the viscosity coefficients areη= 0.89×10-3Pa·s or 0.89×10-4Pa·s, the microsphere moves towardrx=0 µm in thex-axis but moves up and down along thez-axis.After reaching the maximum positionrzmax, it falls into the equilibrium position slowly, respectively, taking 1.60×10-2s and 2.97×10-3s.It is also verified in Figs.4(c) and 4(d) that the optical forcesFoptical,xandFoptical,zincrease first and then decrease with the particle reaching close to the balance position.In this short period, the particle has experienced the process of acceleration and deceleration.Meanwhile, when the fluid viscosity isη=2.47×10-5Pa·s, the corresponding damping coefficient isβ= 53.47 kHz, which is close to the critical damping.Microspheres quickly reach the equilibrium state both in thex-axis andz-axis, taking 5.15×10-4s.When the fluid viscosity isη=0.89×10-5Pa·s, the micro-sphere will oscillate back and forth, but tends to balance monotonously.It takes 1.09×10-3s to reach the equilibrium position.When the viscosity coefficientη=0.89×10-6Pa·s is near the vacuum environment,β=1.92 kHz,which is less than the natural frequency of the optical trap.The system damping is too small and the viscous force on the micro-sphere is small, as displayed in Figs.4(e) and 4(f), which leads the particle to move back and forth around the equilibrium position.Due to the resultant forcesFsum,xandFsum,zin different dimensions of space,the particle circles around the laser center.With the increase in time, the oscillation amplitude and speed of the micro-sphere gradually decrease.This system’s kinetic energy dissipation is zero and the micro-sphere reaches the equilibrium position.
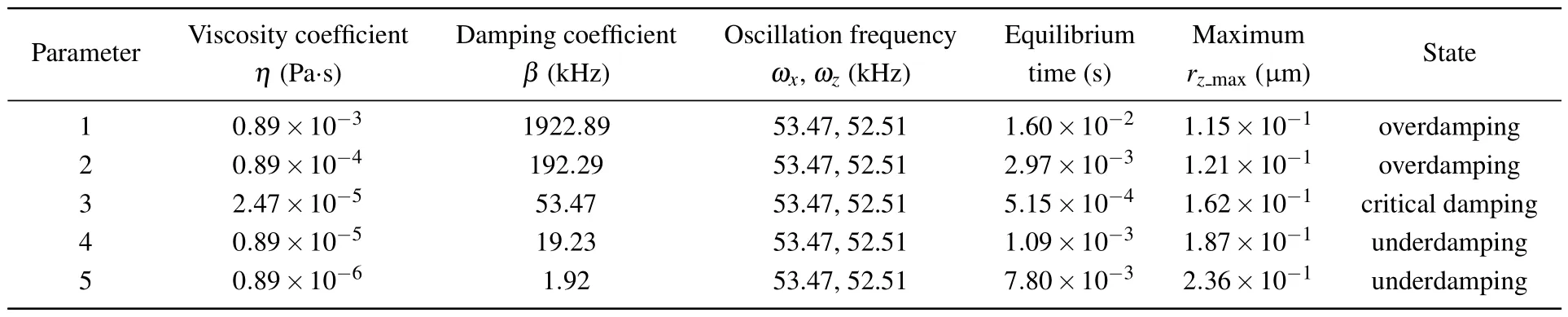
Table 2.The relevant physical parameters of the micro-sphere with different viscosity coefficients at the initial position r0=[1,0,0.085]µm.
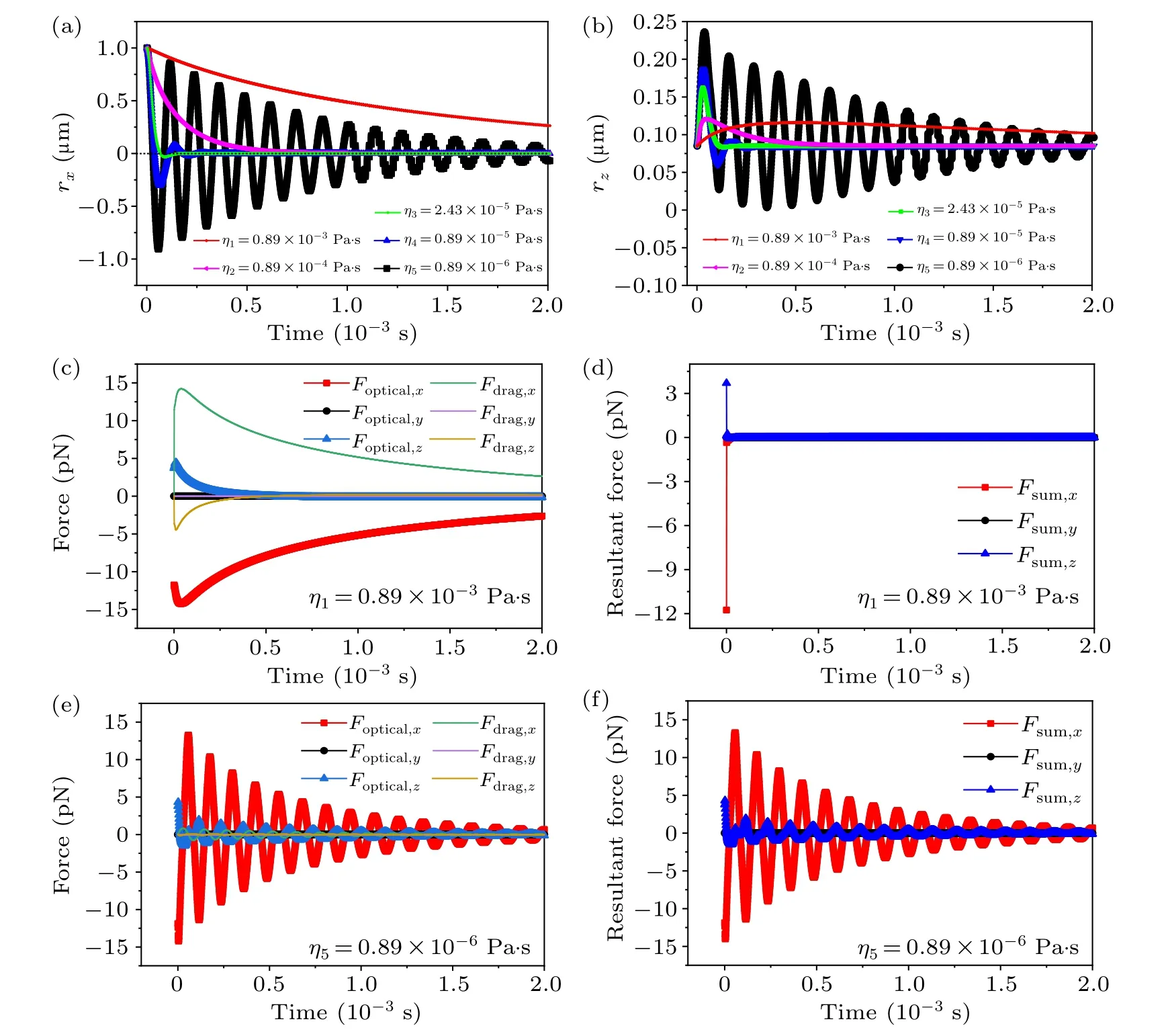
Fig.4.The(a)x-directional trajectories and(b)z-directional trajectories of the micro-sphere in liquids with different viscosity coefficients,and η=0.89×10-3,0.89×10-4,2.47×10-5,0.89×10-5,and 0.89×10-6 Pa·s at the initial position r0=[1,0,0.085]µm and the initial velocity v0=[0,0,0]µm·s-1 in the optical tweezers.The temporal evolution of the x-,y-,and z-directional[(c)and(e)]optical force and drag force,and[(d)and(f)]resultant force of the micro-sphere with viscosity coefficients η1=0.89×10-3 and η5=0.89×10-6 Pa·s,respectively.
Figure 5 shows the 3D trajectories of the micro-sphere in the surrounding medium with different viscosity coefficients,andη=0.89×10-3Pa·s,0.89×10-4Pa·s,2.47×10-5Pa·s,0.89×10-5Pa·s,and 0.89×10-6Pa·s.The corresponding dynamic motions can be observed in the supplementary materials video S2.Table 2 displays the relevant physical parameters of the micro-sphere with different viscosity coefficients.As can be seen in Fig.5, the micro-sphere moves along the complex reciprocating curve.Even in this simple optical tweezer, the dielectric micro-sphere exhibits abundant phases of mechanical motions,including acceleration,deceleration,and turning.But in real experiments, it increases the difficulty in judging whether the micro-sphere is captured in the low viscosity coefficient surrounding medium due to the large vibration offset and the long equilibrium time.
The viscous coefficient is essential to the trapping probabilities and the equilibrium time.When the viscosity coefficient is relatively large, the micro-sphere slowly moves toward the equilibrium position.When the corresponding damping coefficient is close to the optical oscillation frequency of the optical tweezers, the particle takes the minimum time to rapidly reach the equilibrium position.When the viscosity coefficient declines,the damping coefficient is less than the optical oscillation frequency of the optical tweezers.The particle exhibits oscillation behavior,and takes more time to reach the equilibrium state.The entire process of particle manipulation is of short duration,and the position offset of the micro-sphere is small.So, the dynamic process of the micro-sphere in the initial period is one that is subtle and easily overlooked point.And this dynamic analysis method has contributed to research on the working mechanism of DNA-related proteins with a micro-sphere handle.[25-27]
6.Conclusion
In summary, based on the equations of Newtonian mechanics, we have studied the kinetic problems of lasertrapped micro-spheres in liquids with different viscosity coefficients.Through the fourth-order Runge-Kutta method,we have deduced the equilibrium time, position, and force(Foptical,Fdrag,G,Fbuoy)of micro-spheres in motion.We have visualized the motion trajectories of micro-sphere under different viscous forces by simulating and analyzing the dynamics.We have found that, unexpectedly, the micro-sphere will not necessarily be stabilized quickly even if the viscous force is small.Instead,when the viscosity coefficient reaches an appropriate intermediate value,the system is in critical damping and the micro-sphere tends to stabilize in the shortest time.Moreover, by estimating the stiffness of optical tweezers and the viscosity coefficient of surroundings medium, we can get the dynamic state of micro-spheres to certain systems under the conditions of overdamping, critical damping, and underdamping.
This approach of solving and analyzing micro-sphere kinetic processes from a three-dimensional scale is crucial for a variety of engineering mechanisms in biology or in the field of macromolecules.In the future,we will continue to investigate the kinetic theory of the micro-sphere and will consider more factors such as the physical properties of the particles,photothermal effects, different environmental conditions, and solving complex dynamic problems of different particles.
Acknowledgments
Project supported by the National Natural Science Foundation of China(Grant No.11804399),the Special Funds for Basic Scientific Research at the Central University of South-Central University for Nationalities (Grant No.CZQ20018),and Special Funds for Basic Scientific Research at Central Universities(Grant No.YZZ17005).
- Chinese Physics B的其它文章
- Corrigendum to“Reactive oxygen species in plasma against E.coli cells survival rate”
- Dynamic decision and its complex dynamics analysis of low-carbon supply chain considering risk-aversion under carbon tax policy
- Fully relativistic many-body perturbation energies,transition properties,and lifetimes of lithium-like iron Fe XXIV
- Measurement of the relative neutron sensitivity curve of a LaBr3(Ce)scintillator based on the CSNS Back-n white neutron source
- Kinesin-microtubule interaction reveals the mechanism of kinesin-1 for discriminating the binding site on microtubule
- Multilevel optoelectronic hybrid memory based on N-doped Ge2Sb2Te5 film with low resistance drift and ultrafast speed

