Effective suppression of beta oscillation in Parkinsonian state via a noisy direct delayed feedback control scheme∗

Hai-Tao Yu(于海涛), Zi-Han Meng(孟紫寒), Chen Liu(刘晨), Jiang Wang(王江),†, and Jing Liu(刘静)

1School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China

2Department of Neurology,Tangshan Gongren Hospital,Tangshan 063000,China

Keywords: basal ganglia,neural networks,Parkinsonian state,noise,delayed feedback

1. Introduction

Changes in the neuronal firing rates and the abnormal synchronous bursting activities in basal ganglia (BG) in the Parkinsonian state are generally recognized to be induced by the deficiency of dopamine in the brain.[1]The pathological beta (12-35 Hz) synchronization destroys the reliability of thalamus (Th) neurons to relay the sensorimotor signals, which causes Parkinson’s disease (PD) symptoms like tremor and akinesia.[2-4]Suppressing abnormal beta oscillations plays a key role in alleviating PD state. Now, deep brain stimulation (DBS), especially that with high frequency(＞120 Hz),is effective in regulating the pathological neuronal activities via injecting electrical pulses into the BG nucleus such as the subthalamic nucleus (STN), the internal and external globus pallidus(GPi and GPe).[5-8]Nevertheless,DBS performs poorer in energy utilization due to its intrinsic openloop properties,[9-12]which decreases the battery life and increases the risk of device replacement surgeries. Thus, the further development of DBS is restricted.

The abnormal synchronous exist in the BG network in the PD state. Suppressing the synchronous is beneficial to alleviate the PD symptom. The delayed feedback strategy is a typical closed-loop control method in neuronal desynchronization,which adjusts the stimulation signals to adapt to the condition of the synchronized neuronal activity in real time.It has a simple desynchronization mechanism and becomes popular since proposed by Pyragas.[13-18]It has been proved that different types of delayed feedback control algorithms(e.g., direct delayed feedback (DDF) and multiple-delayed feedback) have significant effects in desynchronizing neural network.[19,20]Thus, more and more researchers apply it to the disturbance of the abnormal neuronal synchronous activities. In our previous work, the linear differential delayed feedback control algorithm was used to suppress pathological oscillations based on a neural mass model and was testified robust and effective with four types of stimulus source and target combinations.[21]M. Daneshzand used the linear differential delayed feedback control strategy to modulate the frequency of DBS and demonstrated it suppresses abnormal beta oscillations in PD state robustly and strongly.[5]

Noise is necessary for neuronal dynamical performance.It has been proved that spatiotemporal noise with appropriate parameters can enhance the spread of weak neural electrical information.[22-24]A novel noise stimulus has been proposed and explored in our previous work, in which we applied an open-loop noise stimulus to the BG nuclei and demonstrated its effectiveness in suppressing the abnormal beta oscillations in the PD state.[7]However,the noise stimulus cannot be modulated adaptively in an open-loop control strategy, which induces unnecessary energy expenditure. Thus, the direct delayed feedback control algorithm is applied to adjust the parameters of noise stimulus in this work.

In this study,we mainly explore the function of the noisy direct delayed feedback(NDDF)control strategy in suppressing the pathological oscillations in the BG with PD. We first establish a computational model of the BG-Th neuronal network and describes the NDDF control strategy. Then,we are devoted to presenting the effects of NDDF on pathological activities alleviation and analyzing the impacts of the main parameters. Additionally, we also explore the multiple-NDDF control strategy. Finally,we discuss the reason for inferior periodic in effective parameter region in NDDF and limitations.

2. Methodology

2.1. Model of BG-Th network

In this work,we use the BG-Th neuronal network model modified in Ref. [6], originally proposed by Rubin and Terman in Ref. [25]. The BG-Th neuronal network model has been constructed to present behaviors in the normal physiological state and PD state.[6]The main neuronal structures of the BG-Th network model include Th, STN, GPe, and GPi nuclei. As Fig.1 shows,each nucleus has a population of 100 neurons with their excitatory and inhibitory interconnections.Each STN neuron is inhibited by 2 GPe neurons. Each GPi neuron is excited by an STN neuron and inhibited by a GPe neuron. Each GPe neuron is excited by 3 STN neurons and inhibited by 2 GPe neurons. Besides,each Th neuron is inhibited by a GPi neuron and excited by a cortical input.

Fig.1. The BG-Th neural network structure. Each nucleus has a population of 100 neurons. These nuclei are connected through excitatory(red arrows)and inhibitory(blue arrows)synapses. Each GPi neuron is excited by an STN neuron and inhibited by a GPe neuron. Each STN neuron is inhibited by two GPe neurons. Each GPe neuron is excited by three STN neurons and inhibited by two GPe neurons. Th neurons received ISM (pink arrow)from the cortex.

where gj→iis the coupling strength from neuron j to neuron i. In this work, we hypothesize that the coupling strengths are identical for all pairs within two specific nuclei. vI,iis the membrane voltage of neuron i in I nucleus, and τI,iis the synaptic delay. Ej→iis the reversal voltage determining the synaptic type with Ej→i=0 mV for excitatory synapses and Ej→i=−80 mV for inhibitory synapses. rjis the fraction of the post-synaptically bound neurotransmitter

As the synaptic decay rate, the tswas set to 10, 5, and 100 for the STN,GPe,and GPi neurons,respectively. Explicit parameter values are listed in Ref.[6]. Notice that the value of coupling strength from STN to GPi is 0.5 and that from GPi to Th is 0.2 in this work.

2.2. Neuron models

The Izhikevich model[26]is widely used due to its advantage in simulation. And it can simulate the dynamics of BG and Th neurons, which contributes to exploring the mechanism of PD condition.[27]Based on a hybrid Izhikevich model,a large-scale BG-Th neuronal network has been constructed in our previous work.[6]Thus, in order to expand the noise stimulation effects to a larger-scale neuronal network, a hybrid Izhikevich neuron model is used to simulate a single neuron.[28]

The dynamic of a single Th neuron is expressed as follows:

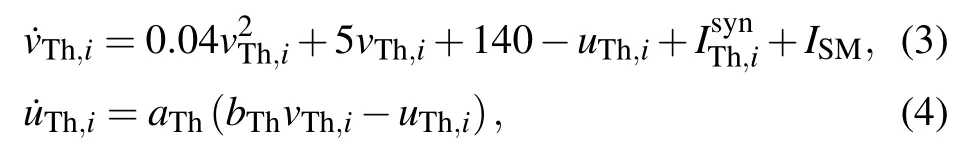
with the auxiliary after-spike resetting rule

Parameters aI, bI, cI, dIdetermine the exact behavior of neurons.[26,30]aIand bIreflect the time scale of uI,iand the sensitivity of uI,ito the subthreshold of vI,i,respectively.In addition,cIand dIare the after-spike reset values of vI,iand uI,iwith I ∈{Th,STN,GPe,GPi}. Notice that uI,iis formulized by an equation like Eq.(4), and the resetting rules of vI,iand uI,iare similar to Eq. (5) with different adjusting parameters list in Ref.[6].

The STN nucleus shows synchronized bursting,which induces rhythmic patterns.[5]Individual STN neurons are modeled by

There are many similar properties between GPe and GPi neurons,particularly continuous repetitive firing patterns. The equations below describe the membrane voltage of GPe and GPi cells:

2.3. Description of the stimulation

For comparison, the traditional high-frequency DBS is utilized. Thus,the stimulation Istimis described as follows:

In the stimulated condition by using traditional DBS condition, 130 Hz DBS pulse trains are only injected into all STN neurons with λ1=1,λ2=0,ρ=1. The expression of IDBSis shown as follows:

where the value of the amplitude ADBS, the period ρDBSand the pulse width δDBSare 300 µA/cm2, 7.69 ms and 0.03 ms,respectively. H(x) describes a Heaviside step function, with the value 0 for x ＜0,1 for x ＞0 and 0.5 for x=0.

The stimulation Istimis adjusted by the DDF control algorithm when λ1=1, λ2=1, ρ =0. The local field potentials(LFPs)of STN nucleus xSTNis the feedback variable.The control method mainly includes two procedures including DDF control scheme, which only considers the time-delayed mean field value without noise:

and NDDF control scheme,which takes into account the noise and time-delayed mean field value:

In addition,xI(t)represents the LFPs of the I nucleus and is formalized by the following equation at time t:

2.4. Evaluation index

In order to validate the effects of the noisy direct delayed feedback stimulation method, the following three indexes are calculated and compared.

2.4.1. Power spectra

Abnormal synchronous activities in the PD state can be detected from the spike times of neurons by calculating the power spectrum.The power spectrum of each nucleus I can be generated based on the Fourier transform of the LFP xI. Note that the first 1000 ms of the simulation results are excluded.

2.4.2. Thalamic reliability

The reliability index (RI) quantifies the ability of the Th neurons to respond to the sensorimotor inputs ISM. In the PD state,the reliability of Th neurons is destroyed with lower RI,

where b and r are the amount of bad driven by ISMand rebound bursts,respectively. n is the total number of ISMpulses.

2.4.3. Energy expenditure

Energy expenditure restricts the application of the noise stimulation in the control scheme mentioned above. Therefore,it is an index for evaluating the performance of the noise stimulation with that of DBS.The total electrical energy is calculated by the following equations:where T denotes the simulation duration. Note that DBS is applied to STN neurons merely with N=100 while the noise stimulation is injected into all BG neurons with N=300.

All simulations are implemented with the forward Euler method with dt =0.1 ms for the duration of 3000 ms. Considering the randomness of the initial conditions and the noise series, all results are obtained from the average results of 30 independent simulation runs.

3. Results

Fig.2. Raster plots of BG-Th neural network and the LFPs for BG network in the(a)normal state,(b)PD state,and(c)stimulated state by the direct delayed feedback control strategy with K=0.21,τ =24. Note that the red pulse train in the spike raster plots of Th nucleus denotes ISM.

Fig.3. Combined impacts of time delay τ and feedback gain K on the(a)thalamic reliability RI and(b)energy expenditure IRMS.

Moreover,the impacts of the main parameters of the DDF control strategy including feedback gain K and time delay τ on the thalamic reliability RI and energy expenditure IRMSare explored.It can be seen from Fig.3(a)that RI is improving since K is up to 0.15,especially at integer multiples of half an oscillatory period. The effective region shows apparent periodicity.In addition, the value of RI is close to 1 around K =0.25,whereas the neural network model is disabled simultaneously.The neuronal activities in DDF control strategy with K=0.21 and τ =24 have been given in Fig.2(c).

Besides, the energy expenditure IRMSfor the different parameter settings is shown in Fig.3(b). We can find that IRMSincreases approximately linearly with the increase of K. Interestingly, the energy expenditure of the DDF control strategy is less than that of traditional high frequency DBS(IRMS=5922 µA/cm2) all the time. Thus, the DDF control strategy performs effectively in alleviating the pathological PD states expending less energy.

It can be seen that the effective parameter region of the DDF control strategy is small from the previous part. In other words, it is difficult to find appropriate values of K and τ to adapt to the change of the condition of patients.It has been testified that the noisy open-loop stimulation strategy is effective in the alleviation of PD in our previous work.[7]Considering the defect of open-loop control strategy,the NDDF strategy is proposed in this work. The NDDF stimulus has been given by Eq. (12), and it can be regarded as an intensity-varied noisy signal.

In order to compare the effects of DDF and NDDF control strategies on suppressing pathological oscillation in the PD state, power spectral densities are calculated under PD, normal, DDF stimulated, and NDDF stimulated states, as shown in Figs.4(a)-4(c),respectively. Compared to the normal state,obvious beta oscillation peaks appear in the PD state. Both DDF and NDDF control strategies can remove the pathological peaks effectively. Under the DDF stimulated state, however,new peaks emerge at 16 Hz and 7 Hz in the GPe and STN nuclei, respectively. The NDDF control strategy, by contrast,suppresses the beta pathological oscillations without inducing any new peaks in other bands.The noise stimulus induces subthreshold oscillations of each neuron, which is similar to the normal state. The possible mechanism of noise stimulation is coherence resonance. The noise stimulus with a low intensity leads to poor ability to change the system’s dynamics. Besides, when noise intensity is excessively high, the neuronal firing becomes random, which changes the system’s original dynamics. Specific research has been provided in our previous work.[7]The results may reflect that the NDDF control strategy is more suitable to improve the PD symptoms than the DDF control scheme. Besides, the traditional high frequency DBS induce new-born oscillations at 130 Hz,which is not presented.

In addition,the thalamic reliability index RI is calculated and given in Fig.4(d). There is an exciting result that the value of RI in the NDDF stimulated state reaches a normal level. The above results fully prove that the NDDF control strategy is more appropriate than the DDF strategy to enhance the reliability of thalamic neurons.

In this work,we feedback the STN-LFP to modulate the noise intensity. In reality, due to signal processing and transmission, there is a time delay in the feedback process. Thus,the time delay τ plays a crucial role in NDDF control strategy designing. Besides,the feedback gain K is also important in adjusting noise strength. The effects of K and τ on thalamic reliability RI are explored in the following. Consider that the mechanism of noise stimulation might be stochastic resonance,[33,34]figure 5 presents the combined impacts of K and τ on thalamic reliability for different initial frequency f0of noise signal by using the two-dimensional parameter spaces. Notice that the value of RI is slightly lower than that in a single simulation, due to taking the average of over 30 simulation results. Obviously,the value of RI is up to a high level in a specific region for an exact initial frequency band. Taking the example of 10 Hz ＜f ＜20 Hz, as shown in Fig.5(b), the value of RI reaches 0.90 within a band domain with 0.4 ≤K ≤1.8, which suggests that the region of effective DDF parameters can be expended by applying noise stimulation due to its randomness. Besides,the value of RI in the NDDF control strategy with f0=10 Hz is higher than that in 1 Hz,50 Hz,and 100 Hz.

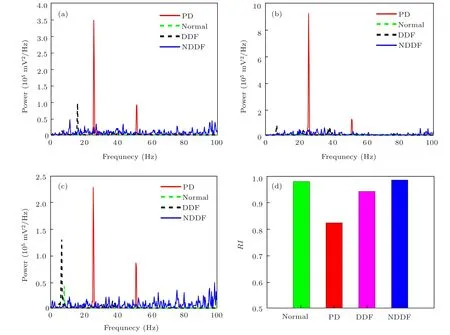
Fig.4.Power spectral density diagrams of(a)GPe nucleus,(b)GPi nucleus,and(c)STN nucleus,as well as thalamic relay index(d)in normal,PD,and stimulated states. Specifically,DDF control strategy with parameters K=0.21,τ =24,and NDDF control scheme with parameters K=1,τ =4 and f0=10.

Fig.5. Combined impacts of feedback gain K and time delay τ on the thalamic reliability RI for different frequency bands in NDDF control strategy. (a) f0 =0.1(b) f0 =10(c) f0 =50 and(d) f0 =100. The solid black line denotes the energy expenditure of high frequency DBS(IRMS=5922µA/cm2).

Interestingly, by comparing the results of noise stimulus in different frequency bands, it can be found that the effective range of feedback gain increases with the enhancement of the initial frequency,which is consistent with previous results that low-frequency-small-intensity or high-frequencylarge-intensity noise signals are effective in enhancing the thalamic reliability.[7]Moreover,the energy expenditure IRMSof NDDF increases linearly with the increase of K,which is not given. Energy expenditure of the NDDF control strategy with K and τ in the domain below the solid black line is lower than that of traditional high frequency DBS. Therefore, the lowenergy and effective NDDF control strategy with smaller K and f0is more suitable to modulate the pathological PD states.

It was demonstrated that the multiple-delayed feedback control method could suppress collective synchrony.[20]Next,we explore whether the beta pathological oscillations can be suppressed effectively by exploiting the multiple noisy direct delayed feedback control. Modifying the multiple-delay control algorithm in Ref. [20], the multiple-NDDF control algorithm is represented as follows:

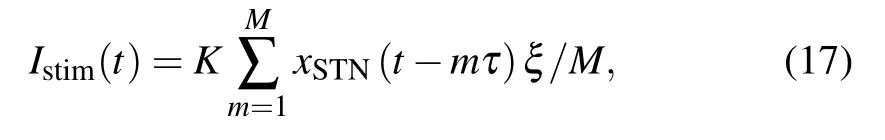
where M presents the multiple of τ. In other words, the multiple-NDDF control scheme used the LFPs of STN nucleus Mτ milliseconds ago. Comparing to the NDDF control strategy,the multiple-NDDF considers more previous LFPs of the STN nucleus,which reflects earlier firing condition of neurons in the BG neural network. And note that the multiple-NDDF is the same as NDDF when M=1.

In order to compare the effects of different multiples of multiple-NDDF control strategy on promoting the thalamic reliability, the combined impacts of K and τ with initial frequency f0=10 Hz are explored and represented in Figs.6(a)-6(e) via two-dimensional parameter spaces. For clarity, the thalamic reliability at 0 ＜K ＜2.8 is displayed.It can be found that the multiple-NDDF control strategy with M ＞1 enhances the value of RI more significantly than that with M =1. In addition,the effective parameter region in the multiple-NDDF control strategy with M ＞1 is larger than that with M =1.Considering the high value of RI at K =1 as Figs. 6(a)-6(e)present,in order to describe the differences between different M of multiple-NDDF control strategy more clearly, Fig.6(f)presents the impact of M on the average RI and its error for different time delay with K=1. It can be found that the value of RI increases first, then decreases with the enhancement of the time multiple M, which indicates that an optimal M exists to maximum RI. Specifically,the optimal value of RI is at M=5.Thus,the multiple-NDDF control strategy plays an important role in alleviating the PD pathological states. And an optimal effect can be obtained by adjusting the time multiple M.

4. Discussion

There are lots of positive and negative synchronization of neurons in the brain neural networks.[35-40]The pathological synchrony appearing in the PD state needs to be suppressed. Many studies have shown that the delayed feedback control strategies play a significant role in desynchronizing neural networks.[5,19,20,41,42]Therefore, from the perspective of neural dynamic characteristics, the delayed feedback control strategy is helpful to the suppression of beta oscillations,which agrees well with the simulation results above. There are many types of delayed feedback control strategies, such as direct delayed feedback and differential delayed feedback control strategies. In this work, we mainly explore the effectiveness of noisy direct delayed feedback control strategy in the treatment of PD.

We have proved that the effective delayed feedback parameter region is periodicity in our previous work.[21]However, from Figs. 5 and 6, the periodicity is absent in the effective NDDF parameter region. Comparing Eq. (11) with Eq. (12), K in Eq. (11) is equal to Kξ in Eq. (12). For the latter, the value of K can be obtained by dividing Kξ by ξ,which results in an extension of the effective parameter range due to the randomness of noise signals.In other words,the periodicity of the effective parameter region is weakened. Thus,the period disappears in NDDF and multiple-NDDF control strategies,as Figs.5 and 6 show.

The above results may bring new methods to alleviate the PD states,but some limitations still exist in our model and control schemes. As for the BG model, we only pay attention to the GPe,GPi,and STN nuclei but do not consider other nuclei in the BG network.[43]Moreover, each nucleus has a population of 100 neurons,which is quite different from the real ones.Therefore, the NDDF and multiple-NDDF control strategies should be further testified on biologically more realistic models and even directly in experiments. On the other hand, the feedback signal is LFPs of the STN nucleus obtained by the embedded and invasive electrode, which will bring trauma to patients. Nevertheless, the above simulation results can provide the guideline of parameter adjustments of the noisy delayed feedback control system.

In this work,we proposed an intensity-varied deep brain noise stimulation strategy, which acquires local field potential signals by using implantable electrodes. The method is invasive. In the future, we will explore the noninvasive transcranial noise stimulation method in alleviating PD symptoms. Accordingly, the electroencephalogram (EEG) signals can be used as feedback signals. Because the EEG signals can reflect the beta rhythm in the PD state. Moreover, the properties of the NDDF and multiple-NDDF control strategies need to be explored,on which the design of adaptive delayed feedback controller is based. Finally, we will devote ourselves to the hardware implementations of the BG-Th neural network model, NDDF control algorithm, and communications between model and stimuli. In this way,the proposed NDDF control scheme will be further developed in the suppression of pathological oscillations in the PD state in animal experiments.

Fig.6. Combined effects of feedback gain K and time delay τ on the thalamic reliability for different multiple M of multiple-NDDF control strategy,(a)M=1,(b)M=3,(c)M=5,(d)M=7,(e)M=9,with initial frequency f0=10 Hz and(f)the impact of M on the average RI for different τ with K=1.

5. Conclusion

In this work, we explore the NDDF and multiple-NDDF control strategies and verify their effectiveness in improving the PD state. The NDDF control strategy is testified and compared with other DBS methods,including traditional high frequency impulse stimuli and DDF stimulus. By applying the NDDF control scheme,the thalamic reliability can be enhanced significantly, and the neuronal pathological beta oscillations in the BG network can be suppressed effectively.The energy expenditure is reduced markedly at the same time.Specifically,the region of effective feedback gain of the DDF control strategy can be extended by using the noise signals due to its randomness. Besides, the NDDF control strategy with appropriate parameters suppresses the beta oscillation without inducing any new peaks in other frequency bands,and the value of the thalamic reliability is close to the normal condition. By exploring the roles of NDDF parameters,we find that small-feedback gain and small initial frequency are more suitable to alleviate the PD state. Furthermore, the multiple-NDDF control strategy is analyzed,and we find that the multiple-NDDF with appropriate parameters performs better than NDDF.In other words,the effects of the NDDF control strategy can be optimized by adjusting the time multiple on improving Parkinson’s symptoms.

This work may provide guidance for the research and application of nonlinear dynamics in improving neurological dysfunction.[44,45]In addition, based on this work, effective treatments for other neurological diseases like Alzheimer’s disease will be developed by establishing the computational model of other brain regions and changing the stimuli targets.[46-48]Moreover, the simulation results may pave the way for the implementation of a novel noisy direct delayed feedback stimuli system. Next, we will concentrate on the experimental evidence, like other DBS patterns,[49-51]which is significant to prove the effectiveness of the NDDF control strategy in affecting the whole neural system via synaptic connections.