Effects of quantum quench on entanglement dynamics in antiferromagnetic Ising model

Yue Li(李玥), Panpan Fang(房盼盼),2, Zhe Wang(王哲),2,Panpan Zhang(张盼盼),3, Yuliang Xu(徐玉良), and Xiangmu Kong(孔祥木),2,†

1School of Physics and Optoelectronic Engineering,Institute of Theoretical Physics,Ludong University,Yantai 264025,China

2College of Physics and Engineering,Qufu Normal University,Qufu 273165,China

3Department of Physics,Beijing Normal University,Beijing 100875,China

Keywords: quantum entanglement, quantum phase transition, quantum quench, quantum renormalization group

1.Introduction

Due to nonclassical correlation properties of quantum entanglement, it has been widely applied in quantum information and computation.[1-8]Nowadays,it has been accepted as a useful tool to describe some important physical phenomena in quantum spin systems, such as quantum phase transition(QPT)which occurs at zero temperature and is driven by quantum fluctuation.[9-16]The equilibrium properties of quantum entanglement and QPT have been extensively studied in some spin systems.[17,18]One of the most representative work is that Osterlohet al.investigated the concurrence in the onedimensionalXYmodel with a transverse magnetic field and found that the entanglement plays an important role in the detection of QPT.[11]Then the Ising,XYandXXZspin chains were studied by the quantum renormalization-group (QRG)method,and it is found that the first derivatives of the entanglements show the scaling behaviors close to the quantum critical points of these models.[19-26]

In recent years, with the advances in experiments of ultracold atom, the dynamical evolution of the spin system has become a frontier problem in the field of condensed matter physics.[27-33]Quantum quench is a typical method which can drive the dynamics of the spin system, and up to now most of the attentions have been devoted to the dynamical quantities following sudden quench.[34-43]In 2013, Karraschet al.applied the matrix product state method to study three types of Ising models in the presence of two additional terms which break integrability, and they found that the rate functions for the return probability to the initial state in all of the Ising models become a nonanalytic function of time in the thermodynamic limit.[37]In 2014, Hazzardet al.investigated the time evolution of quantum correlation and entanglement following three types of quantum quench protocols which are initiated from uncorrelated states that are easily prepared in the experiment using complementary analytic and numerical methods.[38]

However, there are still some open questions in the dynamics of quantum spin systems: How is the relation between entanglement and QPT in quantum quench protocol? Especially, if we adopt both types of quench protocols, what are the different behaviors of entanglement? Does the scaling behavior of entanglement exist? To answer these questions, we study the dynamics of entanglement and QPT in the antiferromagnetic(AF)Ising model with Dzyaloshinskii-Moriya(DM)interaction in both types of quench protocols.The manuscript is organized as follows: The model and QRG method are introduced in Section 2.We analyze the dynamical behavior of entanglement near the critical point In Section 3.Then the nonanalytic and scaling behaviors of the time are discussed in Section 4.We summarize our results in Section 5.

2.Model and method

The Hamiltonian of one-dimensional AF Ising model with DM interaction in thezdirection on a periodic chain ofLsites can be written as

where(α=x,y,z)are Pauli matrices on thei-th site.[44-46]The parameterJ ＞0 denotes the AF coupling andDis the reduced parameter which is related to DM interaction.

Next,we apply the QRG method to discuss the properties of the above system.[47-49]This method not only simplifies the degree of freedom of the system,but also maintains the invariance of the low-energy spectrum,which is very important for exploring quantum problems at zero temperature.A brief introduction to the steps of QRG is following.The Hamiltonian of the system is divided into block Hamiltonian and interblock one.The Hamiltonian of each block is diagonalized exactly,and the double degenerate ground states are kept to construct the basis for renormalized Hilbert space.Then the Hamiltonian is projected onto the renormalized space,and the effective Hamiltonian is obtained.However, the effective Hamiltonian is not exactly similar to the initial one,that is,the sign of DM interaction is changed.To have a self-similar Hamiltonian,we implement aπrotation aroundxaxis on all sites.[23,50]The HamiltonianH0is transformed to

The specific transformation steps are as follows.Considering three sites as a block,the Hamiltonian can be written asH=HB+HBB,whereHBandHBBare the block Hamiltonian and interblock one,respectively,

where

The two degenerate ground states of the threesite block HamiltonianHBkin the space spanned by{|↑↑↑〉,|↑↑↓〉,|↑↓↑〉,|↑↓↓〉,|↓↑↑〉,|↓↑↓〉,|↓↓↑〉,|↓↓↓〉}(where|↑〉 and|↓〉 denote the eigenstates ofσz) can be obtained as

where

The effective Hamiltonian is obtained by bringing the above formula into Eq.(8).For the request of QRG method is that the effective Hamiltonian has a similar structure to the initial one,the effective Hamiltonian is expressed as

where

By analyzing Eq.(13), the fixed points are obtained by only solvingD＇=D.The stable fixed points locate atD=0,∞,and the unstable fixed point(the critical point)locates atD=1.Under QRG iterations, the coupling constantDgoes to zero forD ＜1 and infinity forD ＞1.At the stable fixed pointD=0,the ground state of the system is AF phase(N´eel phase).With the increasing of the DM interaction,the quantum fluctuation destroys the AF order inzdirection and gradually makes spins to be oriented in the “XYplane”.The QPT happens at the critical pointDc=1.ForD ＞1, the system represents a saturated chiral phase.[23]

3.Dynamical behavior of entanglement

In order to study the dynamical behavior of entanglement near the critical point,we adopt the negativity to measure the ground-state entanglement between two sites.The density matrix of the system consisting of two subsystems is positive definite,and the density matrix can be written in the direct product form (ρ=ρ1⊗ρ2) for the separable states.In this case,the partial transposition density matrix is still a non-negative separable matrix（ρT1 =ρT1⊗ρ2）, and its eigenvalues are all positive, otherwise, the system is in the entangled state.[51]Therefore,the negativity is defined as

whereuiare the negative eigenvalues of the partial transposition density matrix,andρis the density matrix for the system of two sites.[52]

Next, we investigate the time evolution of the entanglement by considering two types of quench protocols(i)adding the DM interaction suddenly and(ii)rotatingπaroundxaxis on all sites to drive the dynamics of the system.

Quench protocol (i): The system starts with one of the two degenerate ground states of the pure Ising Hamiltonian

and then make the Hamiltonian change abruptly toHatt=0 to realize quench.In order to apply the QRG method to calculate the entanglement in a large system, we firstly consider a three-spin system.The initial density matrix for this system isρ(0)=|ψ0〉〈ψ0|,where|ψ0〉=|↑↓↑〉is one of the degenerate ground states of the Hamiltonian(three-spin case)

The DM interaction is added att=0, suddenly, and the density matrix for three-spin system at timetcan be obtained byρ(t)=U(t)ρ(0)U†(t),whereU(t)= e-iHtis the evolution operator

in which

Without loss of generality, we trace over the spin 2 and calculate the pairwise entanglement of spins 1 and 3.The reduced density matrix for spins 1 and 3 can be obtained as

where

According to Eq.(14), the negativity for sites 1 and 3 is obtained as

where

SupposingJ=1, the negativityN1(t) versus timetforD=0.9,1.0 and 1.1 is shown in Fig.1.It is found that the negativity starts from zero and oscillates periodically over the time whateverD=0.9, 1.0 or 1.1.This is due to that the initial pure Ising state is separable such that the negativity equals zero,and the AF order competing with saturated chiral order.The variation of the entanglement on left side of the critical point (D=0.9) is different from that of the right (D=1.1).As the length of the chain increases, the amplitude ofN1(t)decreases gradually and finally vanishes when the quench occurs atD=0.9 in Fig.1(a).The reason for this is that AF phase plays a main role when the coupling constantDgoes to zero with QRG iterations.Conversely,the amplitude ofN1(t)in Fig.1(c) increases gradually as the size of the system becomes large when the quench occurs atD=1.1.The running of coupling constantDgoes to infinity at the thermodynamic limit,and the saturated chiral order has main effect on dynamical evolution of the system.When the system is in the critical pointDc, the correlation length of quantum fluctuation is divergent, so the evolutions ofN1(t) coincide with each other for different sizes of the system in Fig.1(b).

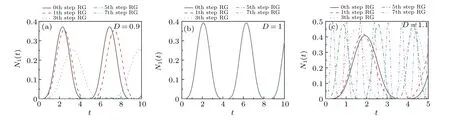
Fig.1.The evolution of N1(t)in terms of QRG iterations versus t (where the unit of time is 1/J)in the quench protocol(i).panel(a)corresponds to the left of critical point,panel(b)corresponds to the critical point,and panel(c)corresponds to the right of critical point.

Quench protocol (ii): Let the system start with one of the degenerate ground state of the HamiltonianH2which can be written as

and then the Hamiltonian is changed toHby implementing aπrotation aroundxaxis on all sites att=0.Similarly,the negativity for sites 1 and 3 can be obtained as

where

Figure 2 shows the relations ofN2(t)versustunder different QRG iterations forD=0.9,1.0 and 1.1.The result is far from the quench protocol(i).The entanglement starts to oscillate periodically from nonzero with timet.ForD=0.9,the amplitude ofN2(t)first increases and then decreases due to the quantum fluctuation caused by spin rotation as the size of the system becomes large and becomes zero atL →∞when the system becomes AF order in Fig.2(a).In the case ofD=1.1, the amplitude ofN2(t)decreases gradually and finally keeps stable because of the influence at the saturated chiral order in a large system.WhenD=1.0,the negativity of different-length chains coincides with each other in Fig.2(b),and the physical cause is the same as the quench protocol(i).

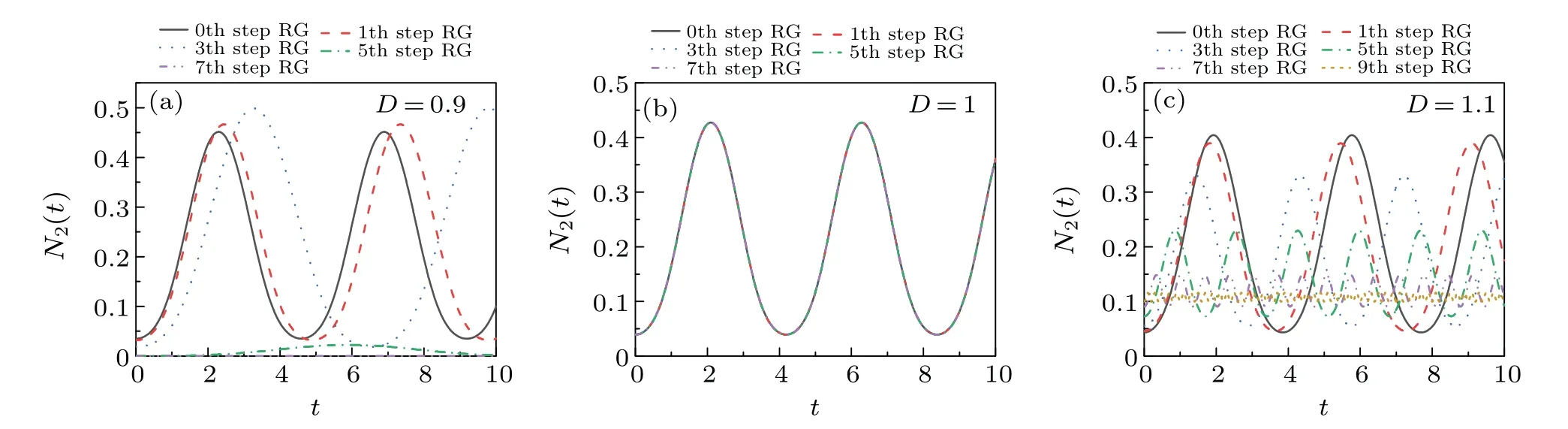
Fig.2.The evolution of N2(t)under QRG steps versus t (where the unit of time is 1/J)in the quench protocol(ii).Panels(a),(b),and(c)correspond to the left of critical point,the critical point,and the right of critical point,respectively.

Next,the evolutions of negativity versusDfort=1.0 in the quench protocols (i) and (ii) are given in Fig.3.For the quench protocol (ii), the negativity oscillates from zero with the DM interaction in Fig.3(a).With the length of the chain increasing, it is found that the oscillation behavior ofN1(D)becomes more and more intense,and the first peak of negativity will approach to the critical pointD=1.0.For the quench protocol (ii), the negativity starts from zero to maximum and then decreases gradually, and finally oscillates slightly at the near of a certain point with the DM interaction increasing in Fig.3(b).The height of each peak decreases gradually and then finally decreases to a fixed value asD →∞.As the size of the system becomes large, the first peak of the negativity also approaches toDc.The fact shows that no matter what quench method is chosen, the entanglement always suddenly changes at the critical point.

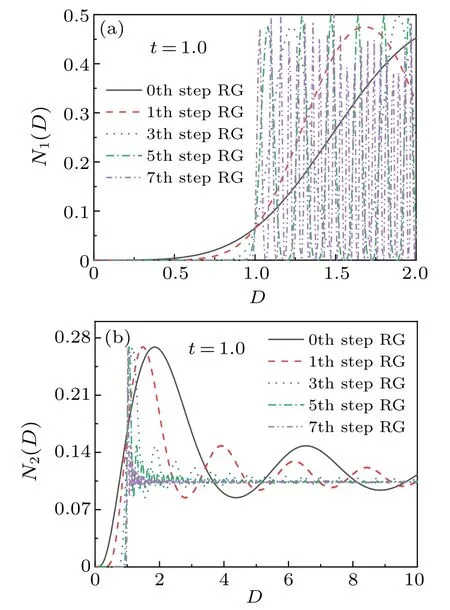
Fig.3.The variation of N1(D) and N2(D) under QRG steps versus D when t =1.0.Panels (a) and (b) correspond to both types of quench protocols(i)and(ii),respectively.

4.Nonanalytic and scaling behaviors

By analyzing the above results,we find that although the system shows different dynamical behaviors in both quench protocols (i) and (ii), there is a same characteristic timeTat which theN1(t) andN2(t) firstly reach its maximum.The characteristic timeTis

The characteristic timeTversusDfor different sizes of the system is given in Fig.4.It is found that the characteristic time decreases with the increase of DM interaction.At the left side of the critical point,Dgradually approaches the stable fixed pointD=0 with the increase of the number of QRG iterations, andTgradually increases.In the thermodynamic limit, the system is in the AF phase.At the right side of the critical point,Dgradually approaches the stable fixed pointD=∞with the increase of the system size,and the characteristic time gradually decreases.By increasing the size of the system,Tdevelops two saturated values gradually atD=1.0,and equation (25) becomes a discontinuous function, which reflects the quantum phase transition from antiferromagnetic to saturated chiral phases.

For understanding the phase transition deeply, the first derivatives of the timeTversusDunder QRG steps are shown in Fig.5.As the size of system becomes large through QRG iterations,the first derivative ofTshows a nonanalytic behavior at the critical point(D=1.0)obtained in Section 2,which indicates that the first derivative of the characteristic time can accurately reflect the quantum phase transition and the characteristic time can characterize the phase transition.

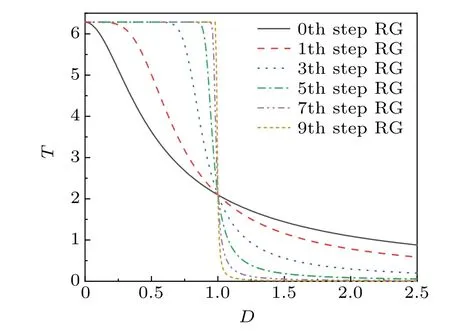
Fig.4.The characteristic time T versus D for different QRG steps.The singular behaviors of T at the large QRG iterations correspond to the emerging of the phase transition.

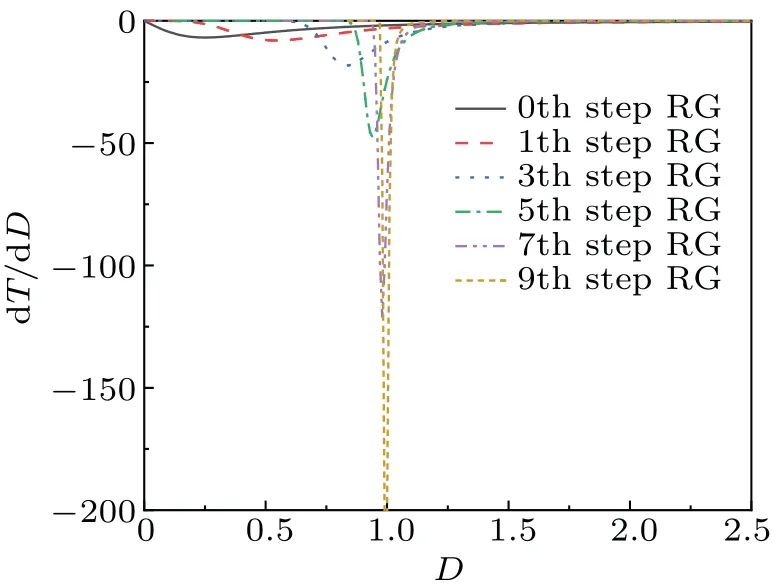
Fig.5.The first derivative of the characteristic time T and its manifestation towards divergence as the number of QRG iterations increases.

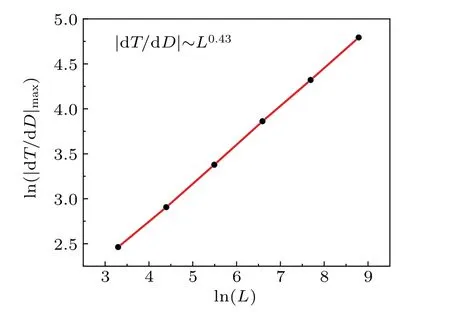
Fig.6.The scaling behavior of the maximum for absolute value of dT/dD versus systems of various sizes.

In order to prove the above case, we calculated the scaling behavior of the maximum of absolute value|dT/dD|max.As shown in Fig.6, there is a linear relation between ln(|dT/dD|max)and lnL,i.e.,|dT/dD|max～Lθwith the exponentθ=0.43(the exponent ofT).The divergent behavior of correlation length in the vicinity ofDccan be written asξ～|D-Dc|-ν.After then-th(n=0,1,2,...)RG steps,the correlation length performs asξn=ξ/bnandξn～|Dn-Dc|-ν,that is,the correlation length diverges atDc=1.0,whereb=3 is the scale transformation factor.Moreover, at the critical point,|dT/dD|Dc～|dDn/dD|Dc.Combining with the above formulas, the relation between the correlation length critical exponentνand exponentθofTcan be obtained asθ=1/ν.The critical behavior of the system can be obtained by the characteristic time of the negativity,that is,the quantum phase transition can be described by the characteristic time.

5.Summary

In this manuscript, the dynamical behaviors of quantum entanglement in the Ising model with DM interaction under two types of quench protocols are studied by using QRG method.The entanglement periodically oscillates over the time for a certain DM interaction, and the variations in the amplitudes of negativity on the left side of the critical point for different QRG steps are different from that of the right in the protocol (i) or (ii).The variations of negativity with DM interaction in quench protocol (i) are different from those of the quench protocol(ii)for a certain time.It is found that the first derivative of the characteristic time can precisely reflect the quantum phase transition from antiferromagnetic to saturated chiral phases.Finally,we investigate the scaling behavior of the first derivative ofTand obtain the relation between the exponents of correlation length and the characteristic time.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No.11675090) and the Natural Science Foundation of Shandong Provincie, China (Grant No.ZR2022MA041).Yue Li would like to thank Li-Zhen Hu,Zhen-Hui Sun,Xiu-Ying Zhang,Qing-Hui Li,and Chuan-Zheng Miao for fruitful discussions and useful comments.