两类三圈图的零度及正负惯性指数

苗 丰,王 龙

(安徽理工大学数学与大数据学院,安徽 淮南 232001)

0 引言

本文考虑的图都是有限的、简单的和无向的.图G是一个连通图,其具有n(G)个顶点和e(G)条边.图的基本圈数c(G)=e(G)-n(G)+1,若c(G)=3,则图G为三圈图.图G的邻接矩阵A(G)={aij}n×n,aij=1当且仅当i～j.G的正惯性指数、负惯性指数以及零度分别记作p(G)、n(G)和η(G),表示A(G)的正、负和零特征值的个数.易知p(G)+n(G)+η(G)=n.G1∪G2表示图G1和图G2不交并.

在量子化学领域,图的零度和正负惯性指数问题有着重要且广泛的应用,在Hückel分子轨道模型中,若分子图G有η(G)>0,则相应的化合物具有高度反应性和不稳定性,或不存在[1-2].在数学中,图的正负惯性指数和零度与邻接矩阵的奇异性等问题相关.在这样的背景下,人们对图的零度的研究主要通过特定的图类着手进行.GUO等[3]刻画了单圈图的零度和匹配数之间的关系.LI等[4]将三圈图分为15类.MA等[5]对树、单圈图、双圈图的正负惯性指数和零度进行了研究.孟霞飞[6]、杨陈[7]等研究了两类特定三圈图的正负惯性指数和零度.本文在此基础上研究另两类三圈图的正负惯性指数和零度,并基于Python语言对三圈图的正负惯性指数和零度进行计算.

1 相关引理

引理1[5]若图G=G1∪G2∪…∪Gt,其中Gi(i=1,2,…,t)是图G的连通分支.则有

引理2[5]在图G中,一条有四个度为2的顶点的路径被一条边替代时,得到图H,则有

p(G)=p(H)+2,n(G)=n(H)+2,η(G)=η(H).

图G如图1所示,其中v1,v2,v3,v4均是度为2的顶点;图H如图2所示.

图1 图G

图2 图H

2 主要结果

设Cp、Cq和Cr是圈长分别为p、q和r的基本圈,形状如图3所示的三圈图称作α-图(α(p,q,r,l,m)),形状如图4所示的三圈图称作β-图(β(p,q,r,l,m,k)),其中路径Pl、Pm和Pk的长度为l-1、m-1和k-1.所有的三圈图可被划分为15类[5],本文研究的两类分别为包含一个α-图为导出子图的三圈图θ1以及包含一个β-图为导出子图的三圈图θ2.对给定的G∈θ1∪θ2,G的导出子图α-图或β-图称为图的核,记为χG.

图3 α-图

图4 β-图

对于α-图(α(p,q,r,l,m))和β-图(β(p,q,r,l,m,k)),令p,q,r∈{3,4},l,m,k∈{2,3,4,5},本文研究的α-图和β-图的一些情况如图5和图6所示,基于Python语言实现对α-图和β-图正负惯性指数和零度的计算,如表1至表13所示.

表1 图α1的正负惯性指数和零度(l≤ m, l,m∈{2,3,4,5})

表2 图α2的正负惯性指数和零度(l,m∈{2,3,4,5})

表3 图α3的正负惯性指数和零度(l≤ m, l,m∈{2,3,4,5})

表4 图α4的正负惯性指数和零度(l,m∈{2,3,4,5})

表5 图α5的正负惯性指数和零度(l≤ m, l,m∈{2,3,4,5})

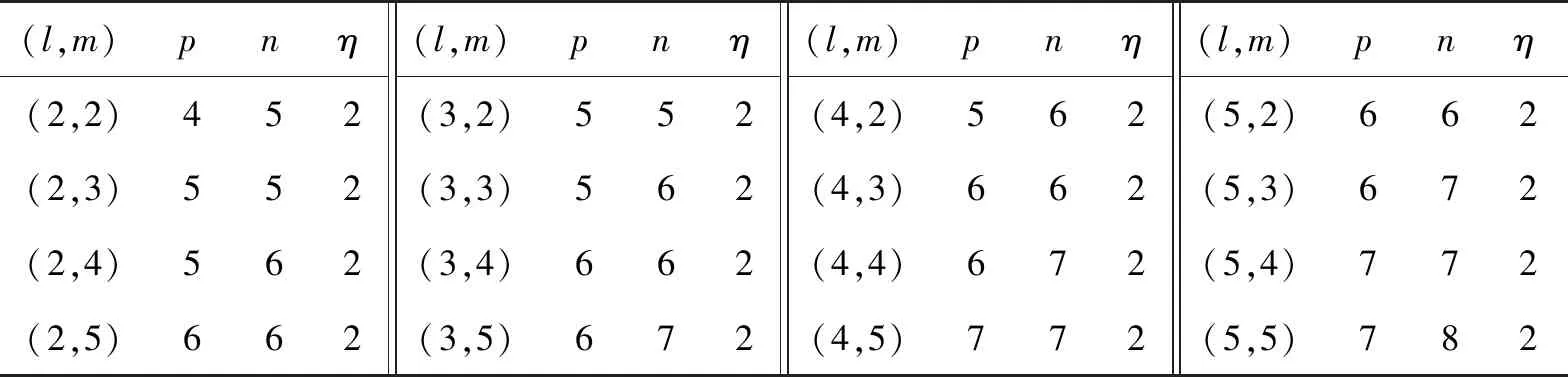
表6 图α6的正负惯性指数和零度(l,m∈{2,3,4,5})

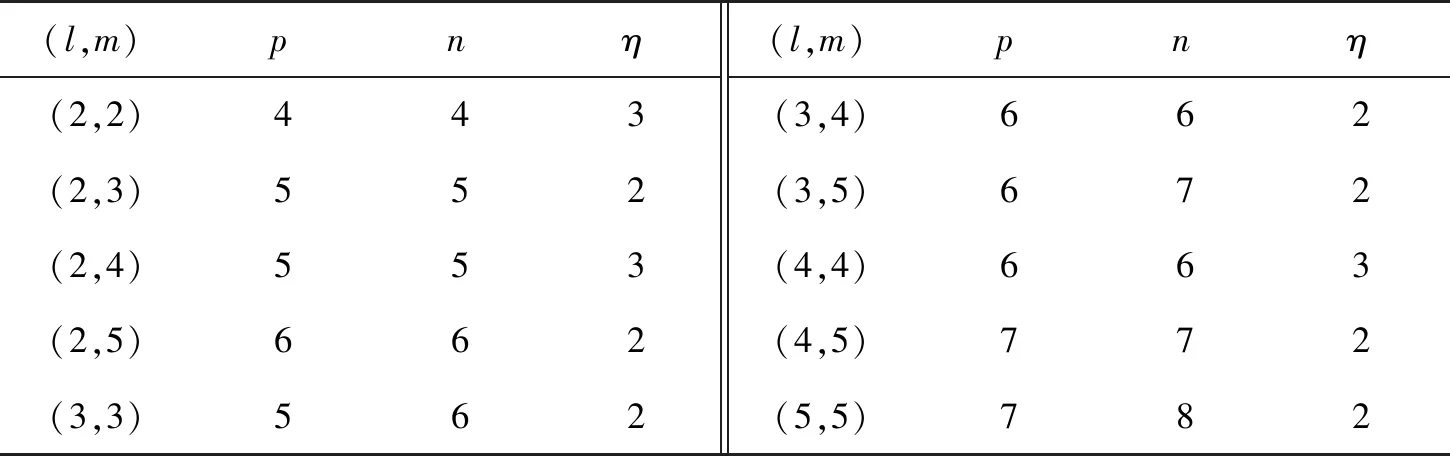
表7 图α7的正负惯性指数和零度(l≤ m, l,m∈{2,3,4,5})

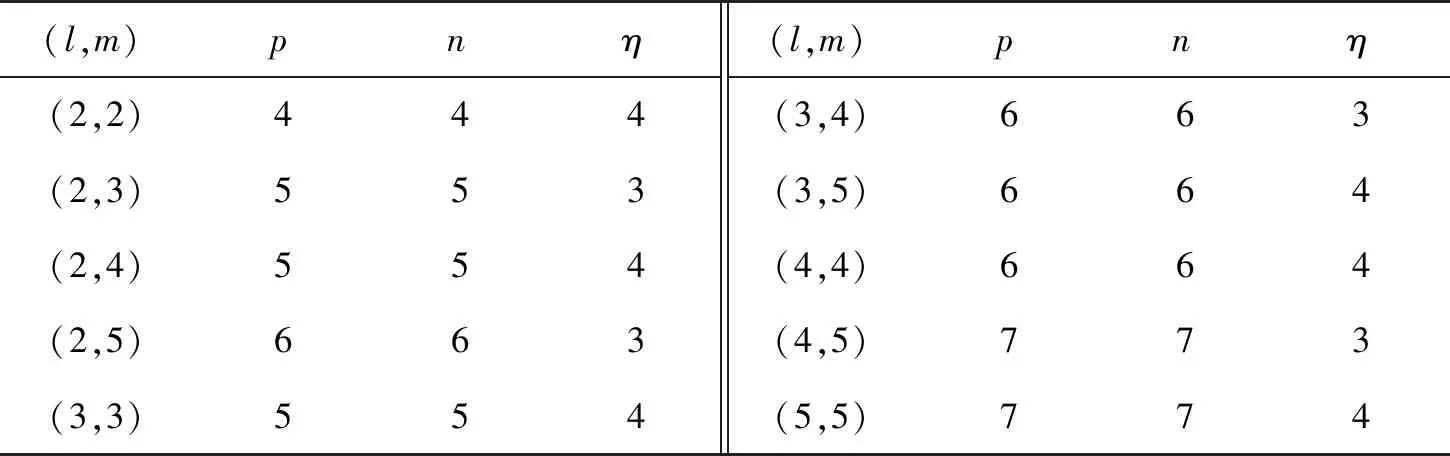
表8 图α8的正负惯性指数和零度(l≤ m, l,m∈{2,3,4,5})

(a)α1

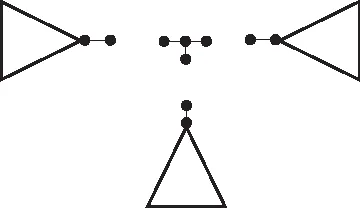
(a)β1

引理3 在三圈图α(p,q,r,l,m)中,p,q,r∈{3,4},l=4g+h,m=4i+j,h,j∈{2,3,4,5},其中g,i为非负的整数,则有

p(α(p,q,r,l,m))=2(g+i)+p(α(p,q,r,h,j)),

n(α(p,q,r,l,m))=2(g+i)+n(α(p,q,r,h,j)),

η(α(p,q,r,l,m))=η(α(p,q,r,h,j)).

证明 由引理2,压缩三圈图α(p,q,r,l,m)内部路易证.

引理4 在三圈图β(p,q,r,l,m,k)中,p,q,r∈{3,4},l=4g+h,m=4i+j,k=4u+v,h,j,v∈{2,3,4,5},其中g,i,u为非负的整数,则有

p(β(p,q,r,l,m,k))=2(g+i+u)+p(β(p,q,r,h,j,v)),

n(β(p,q,r,l,m,k))=2(g+i+u)+n(β(p,q,r,h,j,v)),

η(β(p,q,r,l,m,k))=η(β(p,q,r,h,j,v)).

证明 由引理2,压缩三圈图β(p,q,r,l,m,k)内部路易证.

定理1 在三圈图α(p,q,r,l,m)中,p,q,r∈{3,4},则关于α-图可以分为九类(图5),则关于α-图的零度有以下结论:

(1)η(α1)=η(α3)=0,η(α2)=η(α5)=1,η(α6)=2;

(2)对于三圈图α4,η(α4)=1当且仅当m≡0 (mod 2);η(α4)=2当且仅当m≡1 (mod 2);

(3)对于三圈图α7,η(α7)=3当且仅当l,m≡0(mod 2);其他情况下η(α7)=2;

(4)对于三圈图α8,η(α8)=3当且仅当l≡0(mod 2),m≡1(mod 2)或l≡1(mod 2),m≡0(mod 2);η(α8)=4当且仅当l,m≡0(mod 2)或l,m≡1(mod 2);

(5)对于三圈图α9,η(α9)=2当且仅当l,m≡0(mod 2);η(α9)=3当且仅当l≡0(mod 2),m≡1(mod 2)或l≡1(mod 2),m≡0(mod 2);η(α9)=4当且仅当l,m≡1(mod 2).

证明 由表1至表9可得,在三圈图α(p,q,r,l,m)中,p,q,r∈{3,4}时,α-图的九种情况所对应的图的零度.结合引理2,可以得到三圈图α(p,q,r,l,m),其中p,q,r∈{3,4}的零度以及特定零度所对应的情况.由此定理1得证.

表9 图α9的正负惯性指数和零度(l≤ m, l,m∈{2,3,4,5})

定理2 在三圈图β(p,q,r,l,m,k)中,p,q,r∈{3,4},则关于β-图可以分为四类(图6),则关于β-图的零度有以下结论:

(1)η(β1)=0,η(β2)=1;

(2)对于三圈图β3,η(β3)=3当且仅当m,k≡0 (mod 2);其他情况下η(β3)=2;

(3)对于三圈图β4,η(β4)=3当且仅当l≡0(mod 2),m,k≡1(mod 2)或m≡0(mod 2),l,k≡1(mod 2)或k≡0(mod 2),l,m≡1 (mod 2);η(β4)=5当且仅当l,m,k≡0 (mod 2);其他情况下η(β4)=4.

证明 由表10至表13可得,在三圈图β(p,q,r,l,m,k)中,p,q,r∈{3,4}时,β-图的四种情况所对应的图的零度.结合引理2,可以得到三圈图β(p,q,r,l,m,k),其中p,q,r∈{3,4}的零度以及特定零度所对应的情况.由此定理2得证.

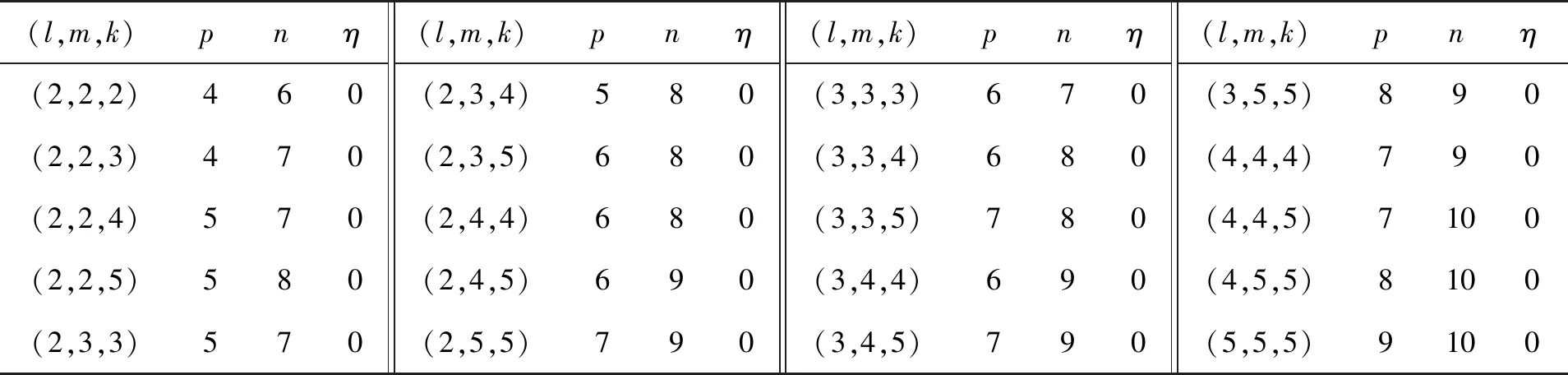
表10 图β1的正负惯性指数和零度(l≤ m≤ k,l,m,k∈{2,3,4,5})

表11 图β2的正负惯性指数和零度(l,m,k∈{2,3,4,5})

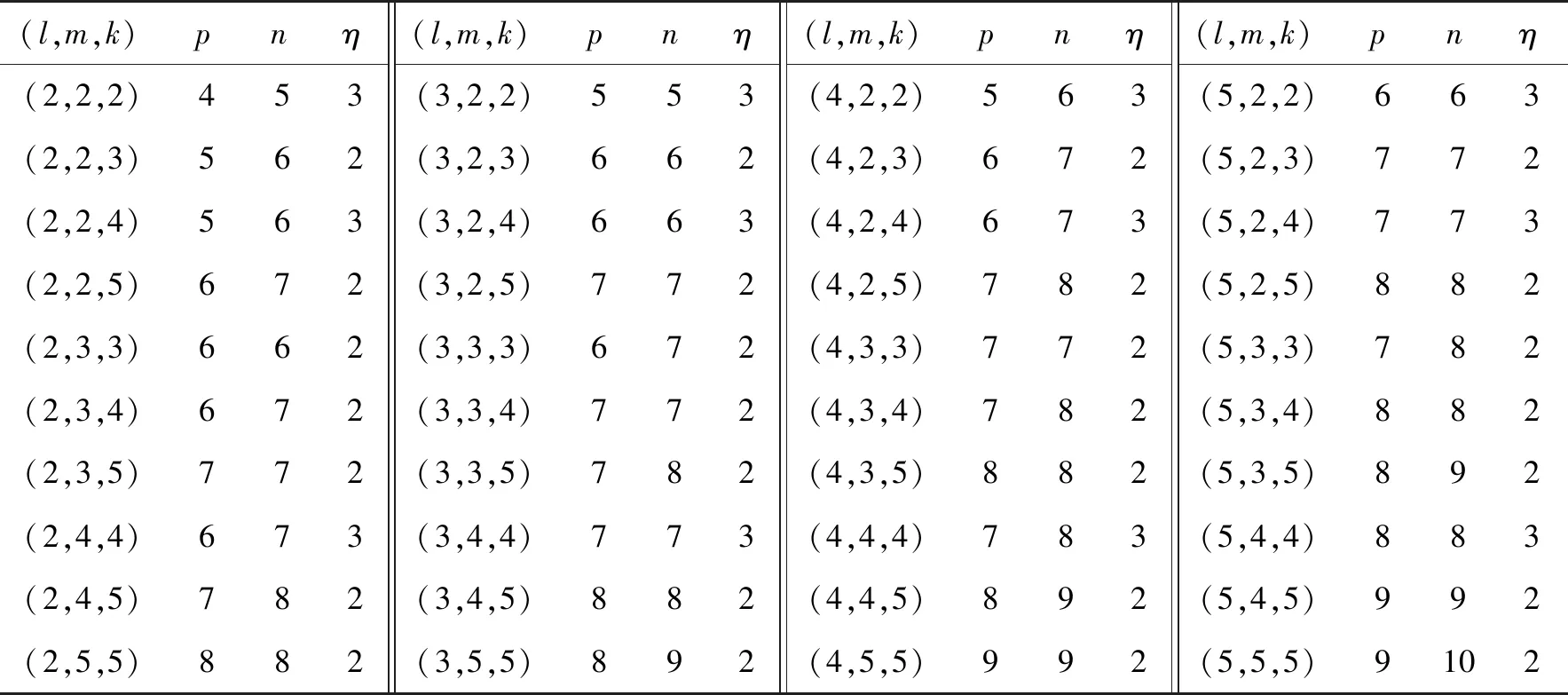
表12 图β3的正负惯性指数和零度(l,m,k∈{2,3,4,5})

表13 图β4的正负惯性指数和零度(l≤ m≤ k, l,m,k∈{2,3,4,5})