大功率风电机组变流器散热系统结构设计
焦守雷, 王成贤
(中车山东风电有限公司,济南 250022,E-mail:jiaoshoulei.sd@crrcgc.cc)
风力发电机组配套的交-直-交大功率变流器,在正常运行时,由于IGBT高频通断、滤波系统以及导电铜排,所产生的热损耗巨大[1],一般在几十个千瓦以上。风电机组运行过程中常因变流器高温问题而停机或限功率运行[2]。变流器常规冷却方式有水冷和强制风冷两种,其中强制风冷型变流器具有明显的成本优势,在行业中愈来愈被广泛应用。风冷型变流器散热基本原理为利用塔架烟囱效应,变流器直接排放的热空气自行往塔架顶部流动[3]。然而,在塔筒外部环境温度较高时及塔筒内部空间相对密闭,极易出现变流器周围空气温度过高,进而变流器进风口温度过高,导致变流器产生高温报警现象,严重影响风力发电机组的正常稳定运行。针对处于相对密闭空间内的变流器进行有效散热设计,是大功率变流器安全、可靠、稳定运行的关键。本文通过变流器-塔筒结合的形式,进行综合热流仿真,对塔架内空间进行传热计算,设计了新型散热系统并进行仿真分析,并展开散热效果对比分析,以确定散热系统是否能满足变流器散热要求。采集分析风电场现场运行数据,以验证计算与分析的准确性,证明散热结构满足工程实际要求。
1 变流器的损耗计算
变流器设计中,损耗主要由三部分组成,分别为并网系统、滤波系统和功率模块系统。并网系统主要为载流的大功率开关器件,损耗约占整体的15%,滤波系统主要为机侧、网侧电抗器、电容器、电阻,损耗约占整体的15%,功率模块系统由三相全控整流、逆变回路和直流母线电容组成,损耗约占整体的70%,其中占比最大的功率模块损耗主要由IGBT模块高频通断和反并联二极管产生,主要为通态损耗和开关损耗。
变流器三相整流和逆变电路采用SVPWM的控制方式,正常输出正弦波电流时的IGBT模块和反并联二极管的通态损耗分别为[4]:
(1)
(2)
式中:I0为实际电流有效值;ψ为实际电流和电压间的相角;M为调制度,它为相电压峰值与方波相电压基波峰值(2VOC/π)之比;TJ为IGBT模块实际结温;Uce25 ℃,UF25 ℃分别为IGBT模块和反并联二极管在25 ℃时的额定导通压降;rce25 ℃,rF25 ℃分别为IGBT模块和反并联二极管在25 ℃时的额定通态电阻;KU_Tr,KU_VD分别为温度对IGBT模块和反并联二极管导通电压影响的温度系数;Kr_Tr,Kr_VD分别为温度对IGBT模块和反并联二极管通态电阻影响的温度系数。
一个开关周期内的IGBT模块和反并联二极管的通态(开通和关断)损耗分别为:
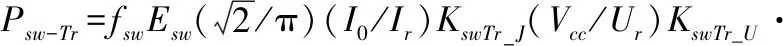
(3)
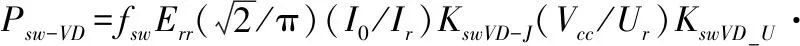
(4)
式中:fsw为载波频率;Esw,Err分别为IGBT模块和反并联二极管额定状态下单脉冲开关损耗;Vcc为桥臂电压;Ir,Ur分别为参考电流和电压;KswTr-J,KswVD-J分别为电流幅值对IGBT模块和反并联二极管开关损耗影响的电流系数;KswTr-U,KswVD-U分别为桥臂电压对IGBT模块和反并联二极管开关损耗影响的电压系数。
实际设计中,变流器整流侧和逆变侧各有三个桥臂,每个桥臂上共有上下2块IGBT模块(含反并联二极管),因此,变流器功率单元总损耗为:
Ptot=12(Pc_Tr+Pc_VD+Psw_Tr+Psw_VD)
(5)
2 塔筒传热计算
变流器设置于塔筒底部平台,塔筒为筒型结构,采用Q355NE材料,可视为大型管状散热器,同时具有烟囱效应,热空气自然向上流动,塔筒进风方式为塔筒门百叶窗自然进风,见图1。
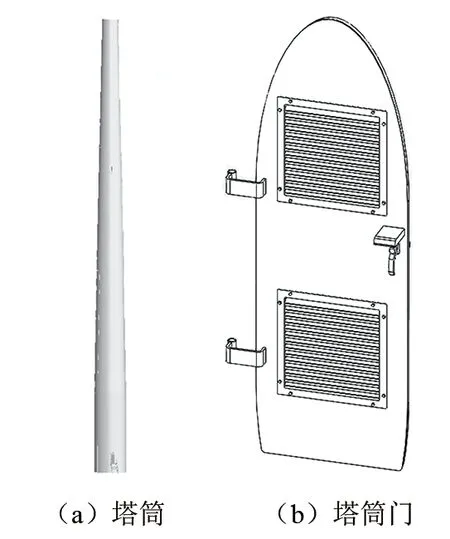
图1 塔筒及塔筒门
塔筒的自散热效能是否能满足变流器的散热要求,则需进行塔筒传热计算[5],主要包括塔筒内表面对流换热系数计算、塔筒外表面对流换热系数计算以及筒壁传热计算,其中以塔筒内外空气作为传热介质。以某3 000 kW型风电机组塔筒和变流器为研究对象,塔筒传热计算参数设置见表1。
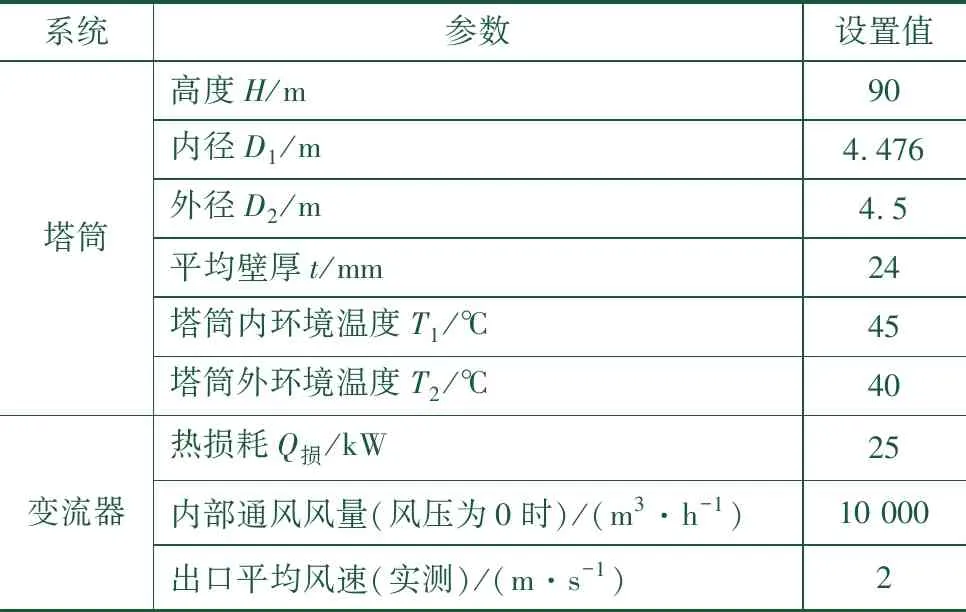
表1 塔筒传热计算参数设计
2.1 塔筒内壁对流换热系数计算
初始输入条件为表1中的变流器出风口平均风速,建立变流器及塔筒底平台模型,利用热流仿真软件模拟计算可得到塔筒内空气的速度分布及流线图[6],见图2。由图2(b)可以得知,变流器出风口热气流上升,垂向筒壁并沿其向上形成贴附流,不会形成紊流状态,见图2(b)A区;而变流器出口下方的热气流,在塔筒底部处形成涡流区,即换热盲区,见图2(b)B区。
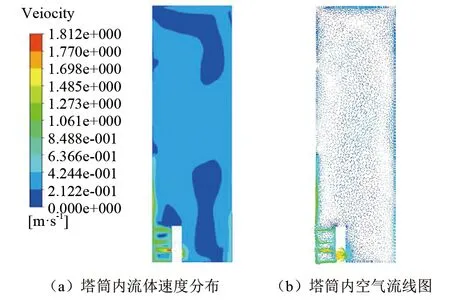
图2 塔筒内空气的速度分布及流线图
以变流器进风口、出风口处0.5 m范围的空气作为分析对象,利用仿真软件计算其在塔筒内随高度变化的流速,得到出口处最大流速为1.8 m/s,最小流速为0.15 m/s,平均流速为1.43 m/s;进风口最大流速为0.9 m/s,最小流速为0.15 m/s,平均流速为0.82 m/s。计算变流器进、出风口的平均速度,作为塔筒内部空气的计算流速,即Vavg1=(1.43+0.82)/2=1.13 m/s。
塔筒内部的空气对流散热方式可视为被动对流,利用Dittus-Boelter公式[7]计算对流换热系数Kin。
Nu1=0.023×[(Vavg1×D1)/v]0.8×0.70.3=
0.023×[(1.13×4.476)/(1.6×10-5)]0.8×
0.70.3=521.2
(6)
Kin=Nu×λ0/D=521.2×0.027/4=
3.518 W/(m2·K)
(7)
式中:Nu为空气努塞尔数;λ0为空气导热系数,为0.027 W/(m·K);ν为空气运动粘滞系数,为1.6×10-5m2/s。
2.2 塔筒外壁对流换热系数计算
塔筒外壁对流换热系数可用外掠圆管对流换热公式[8]进行计算:
(8)
式中:C为常数,由实验数据整理而得;Re为塔筒外壁空气雷诺数;n为常数,由实验数据整理而得;Pr为空气的普朗特数。
计算公式中各参数的选择范围见表2。

表2 计算系数选择范围
本文考虑风电机组运行的各类工况,计算条件为塔筒外空气流速1 m/s至8 m/s。空气流速为 1 m/s时,塔筒外壁冷却空气的雷诺数Re1为[9]:
Re1=(V1D2)/v=(1×4.5)/(1.6×10-5)=2.82×105
(9)
式中:V1为空气流速,1 m/s;D2为塔筒外径。
空气流速为1 m/s时,由表2可知,C=0.026 6,n=0.805,计算得出塔筒外壁空气努塞尔数:
Nu2=0.026 6×(2.82×105)0.805×(0.711)1/3=580.1
(10)
则塔筒外壁冷却空气对流换热系数:
Kout1=Nu2×λ0/D2=
580.1×0.027/4.5=3.481 W/(m2·K)
(11)
以此类推计算,空气流速为(2~8)m/s时塔筒外壁的换热系数,见表3。

表3 不同空气流速下塔筒外壁传热系数
2.3 塔筒壁传热计算
将塔筒内壁冷却空气的对流传热系数Kin=3.518 W/(m2·K)、塔筒材料Q355NE的导热系数λ=46 W/(m2·K)、塔筒外壁冷却空气的对流传热系数Kout[风速(1~8)m/s]、塔筒内部空气温度T1=45 ℃、塔筒外壁空气温度T2=40 ℃代入公式[10]:
(12)
计算得出不同风速下单位长度塔筒壁面传热值,见表4。

表4 不同风速下单位长度塔筒壁面传热值
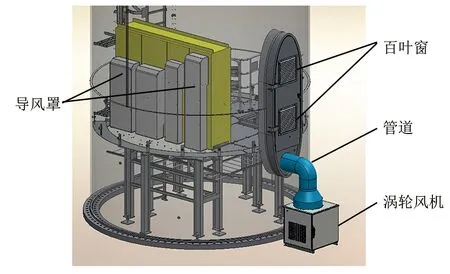
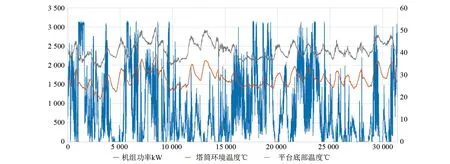
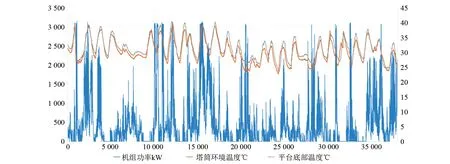
假设塔筒内壁气流连贯、内外空气温差恒定且塔筒内壁空气平均流速≥1.13 m/s,取塔筒外壁空气流速为8 m/s,则整个塔筒壁的传热量Q=Q1×H=207.74×90=18.7 kW 通过计算可知,通过塔筒门自然进风、塔筒内热空气烟囱效应的自然排风方式,塔筒壁的传热量是无法满足变流器通风散热要求的,因此必须增加通风散热设施。 将变流器产生的热量直接排至塔筒外,是最直接有效的散热方式。塔筒门的百叶窗是冷却空气进入塔筒内部的唯一通道,故考虑排出的热量必须远离百叶窗,避免热量被重新吸入塔筒。因此在塔筒门下方设计远离塔筒门的通风管道[11]。 考虑将变流器产生的热量,经导风罩进入塔筒底部空间进行汇集,在塔筒门下方设置通风管道并增设涡轮风机[12],增强通风管道内外风压,加大排风速度,达到增加散热效率的效果。为避免风量泄漏,导风罩、通风管道等之间充分考虑了端面间、密封环及环与端面间的机械密封[13]。且涡轮风机的选型比较了不同风机在相同工况下压力场、速度场和流线分布[14],在满足变流器温升要求的前提下,选取了最经济的涡轮风机,见图3。 图3 散热系统结构图 建立塔筒内部热仿真模型,进行散热设计仿真,见图4。 图4 热仿真模型及分析结果 通过仿真分析可知:由于变流器的热量集中排放到塔基平台底部空间,塔基层温度上升约1.6 ℃,塔基平台底部空间温度受变流器出风影响,温度上升约18 ℃,最高温度约62.718 ℃。轴流风扇入口处,温度上升约12 ℃,最高温度约56.2 ℃。但此方案将变流器所有热量排入底部空间,对底部电缆、自用电变压器等电气设备使用寿命影响较大,将带来老化、破损、绝缘等风险,影响风电机组的正常稳定运行,因此需对此方案进行优化。 在上述方案的基础上,设计集风罩及导风管路,将变流器产生的热量在单独的空间内汇集并排出塔筒外。通过计算分析,导风管路截面积影响外部涡轮风机气流流通能力,选取合适的管道界面,可有效减少风扇尖部气流分离区,使冷却系统风量获得提升[15]。见图5。 图5 优化后的散热系统结构图 建立塔筒内部热仿真模型,进行散热设计仿真,见图6。通过仿真分析可知:变流器产生的所有热量经过集风罩全部导入到风管中,塔基层温度上升较小,塔基平台底部环境温度上升在1 ℃之内,最高温度约45.4 ℃,基本与塔筒内假设温度一致,轴流风扇出风口温度上升约18 ℃,最高温度为60.5 ℃。变流器产生的热量汇集后全部排出塔筒外,有效避免了高温环境对电缆、自用电变压器等电气件因受热发生老化、破损的风险,有效保证了风电机组的正常运行。 图6 热仿真模型及分析结果 目前,本文所述的大功率风力发电机组变流器散热系统已成功运用到某风电场3 MW机组。为对比变流器散热系统结构设计与优化后的效果,在项目现场选取两台距离相近、地理环境相似的风电机组,其中一台机组采用集风罩汇集热量并在涡轮风机作用下经导风管排出,以模拟优化后的变流器散热结构设计;另一台为未安装集风罩及导风管,以模拟优化前的设计,即热量直接排至底平台并在涡轮风机作用下排出。 风电机组启动并正常运行后,对塔筒环境温度、底部平台温度进行数据采集,经过高温季节(8月份)运行后,对相关数据进行分析对比,其8月份运行数据对比如图7、图8所示。 图7 优化前(无集风罩及导风管)的变流器散热方案实测数据分布曲线 图8 优化后(有集风罩及导风管)的变流器散热方案实测数据分布曲线 通过现场运行数据可以看出,风机正常运行时,优化前的变流器散热方案,塔筒环境温度最高为39.1 ℃,底部平台最高温度51.4 ℃,两者平均差值约12.5 ℃;优化后的变流器散热方案,塔筒环境温度最高39.5 ℃,底部平台最高温度40.3,两者平均差值约0.96 ℃。 通过采集的数据与仿真计算结果对比并分析,现场运行数据与仿真计算结果近似。优化前的变流器散热方案底平台平均温升约12.5 ℃,最高温度51.4 ℃,已超出底平台电缆、自用电变压器等电气设备正常运行温度范围。优化后的变流器散热方案,底平台最高温度为40.3 ℃,相对塔筒环境温升约1摄氏度,基本为集风罩、导风管辐射热,冷却效果较好,对底平台电缆、自用电变压器等电气设备无影响,优化后的变流器散热系统整体满足变流器散热需求。 本文讲述了大功率变流器的热损耗计算原理,将塔筒作为圆管型散热装置,通过关键参数设置,建立仿真模型,通过仿真分析,得到比较直观的塔筒内流体速度分布及流线图,并利用Dittus-Boelter等公式进行塔壁的热量传递计算。根据计算结果进行变流器散热装置的结构设计,利用热流仿真技术对变流器的通风与散热进行仿真计算,然后结合仿真结果对变流器散热装置的结构设计进行优化,为风冷型变流器的通风散热提供了理论依据。最后,通过在风电场高温季节的温度数据采集及分析,与仿真计算结果进行比较,对比分析了大功率变流器散热系统设计在优化前、优化后的散热性能差异,验证了理论计算与仿真模型计算的准确性,同时给出了大功率变流器散热实测数据分布曲线,证明所设计的散热结构符合工程实际要求,为大功率风力发电机组变流器的散热系统的结构设计与优化提供了重要参考。3 散热系统结构设计、仿真与优化
3.1 结构设计与仿真

3.2 设计优化与仿真


4 实测对比与分析
5 结论

