巧用身边工具测量降水量

◆安徽省太和县宫集镇中心学校 王伟民

安徽省阜阳市教育科学研究所 杨培军

正弦定理是三角形的一个基本定理，揭示了三角形的边角关系。课堂教学中，如果能将正弦定理与生活实践结合，可使枯燥乏味的理论知识变得生动，有效提高课堂教学效率。本文将正弦定理应用于降水量的测量中，帮助学生理解与应用。

一、有“备”而来测降水量

如何借助简单器具测得降水量呢？我们想到了在空旷的地面放置柱状容器，当容器口处于水平时，在一段时间内接收雨水的深度即为该地在这段时间内的降水量。

图1

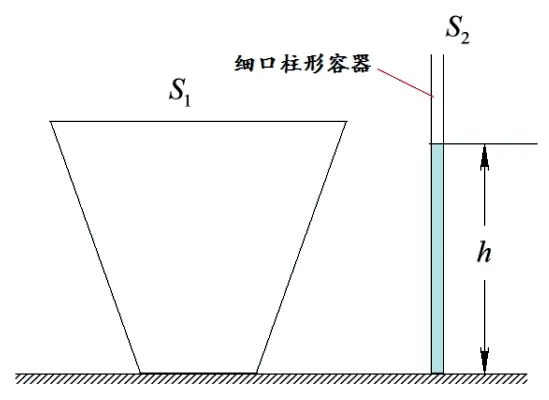
图2

为使测量结果相对精确，我们可以选择一个宽口容器，放在室外空旷且没有遮挡物的地面上。也可将宽口容器放在高层建筑物顶部（如图1），在设定的时段内将容器取回，倒入另一个细口柱形容器（如图2），我们只需测量宽口容器及细口柱形容器的容器开口面积S1和S2，再测量细口柱形容器内倒入水的深度h，就可计算出细口柱形容器内的水倒入宽口容器中时水的深度——即为在选定面积上，一段时间内落到地面未经蒸发、渗透、流失而积聚在水平面上的水层深度，即这一时段内的降水量。

我们用字母A来表示降水量，得出用这种方法测量一段时间降水量的表达式为（长度单位为mm）：

二、巧“算”降水量

假如大雨不期而至，我们并未事先做好测量准备，又该如何测得这次的降水量呢？实际上，在特定情况下，利用特定工具测出相关数据后，我们也能“算”出降水量。

例1：午后天空乌云密布，电闪雷鸣，雨点倾盆而下。

图3

如图3 所示。在一跨度BC=10 m的瓦房屋檐下，有一个长1 m、宽DE为23 cm 的长方体空水池，因承接屋檐滴水而存水32 cm 深。测得雨滴下落方向GA、HC与水平面的夹角为15°，房顶AB、AC与水平面的夹角均为30°，若水池接收的雨水除了正对着水池正上方屋檐滴下的水滴外，还有从空中下落的雨滴。不考虑房顶吸收的水分，试求这十分钟的降水量（取=1.732）。

解析：由图3 可知，如果没有房顶AC面的遮挡，空中洒向房顶AC面的雨水将分散在水平面CF上，因此，水池接收的雨水相当于同时段水平面内宽1 m（长方体水池底面的一边长）、长为DE+CF的水平矩形所接收的雨水量，所以，只要设法求出CF的长即可。

将水池内32 cm 深的水分摊在16 m 长、1 m 宽的水平矩形平面内，水的深度h 为

于是，我们可以得出这十分钟的降水量为4.6 mm。

本文将正弦定理与特定条件下降水量的求解有机融合，让学生深刻认识到数学的广泛应用，学生对降水量也有了更深刻的理解。