洋山港VTS报告船舶流的统计特性

摘要：为分析某水域船舶流特征和运行规律，量化研究船舶流到港规律，为港口营运和船舶交通管理（vessel traffic services，VTS）提供数据支持，以洋山港水域2020年66 d内连续的1387条VTS实测船舶流记录数据为统计样本，基于矩估计理论的K-S检验和χ²检验，从拟合最优的角度对船舶到港情况进行参数估计。结果表明，洋山港水域VTS报告的船舶在8、9月的船舶流样本服从正态分布，7月船舶流样本不服从泊松分布和正态分布，证明船舶流的分布特征随环境和时间因素变化显著，仅采用泊松分布或正态分布并不能全面描述水域交通流特征。相关研究结论可为船舶流特征分析、通航调度等相关研究提供借鉴和参考。

关键词：正态分布；泊松分布；K-S检验；χ²检验；船舶流

中图分类号：U652.1⁺4;U691文献标志码：A文章编号：1672-0032（2023）01-0102-08

引用格式：刘超.洋山港VTS报告船舶流的统计特性［J］.山东交通学院学报，2023，31（1）：102-109.

LIU Chao. Statistical characteristics of vessel flow in VTS reports in Yangshan Port［J］.Journal of Shandong Jiaotong University，2023，31（1）：102-109.

0 引言

研究水路运输中的交通流需要分析水域通航船舶流特征和运行规律，尤其短时间间隔内一定运行强度下的船舶流分布特征，为港口营运和船舶交通管理（vessel traffic services，VTS）的监控、港口调度、进出港船舶流量统计等工作提供理论参考，为提高通航安全、扩大航道通过能力等提供数据支持。在传统观点中，通常假设船舶到港时间服从随机分布，即船舶到港频率与实际情况无直接关联。但刘敬贤等^[1]收集天津港某一主航道内历史船舶交通流，采用分布统计方法对船舶到港时间进行分布统计拟合，发现船舶在1 d不同时刻到达该港口的规律明显服从正态分布，并求得该水域对应的分布参数；余劲等^[2]采用正态分布模型描述船舶在1 d不同时刻到达西江航道的规律，较好地表征水域内船舶的到港规律；文献[3-7]基于船舶大数据的交通状态识别和神经网络预测交通流量；吴中等^[8]基于场方法分析和预测船舶交通流。但正态分布模型在预测船舶的到港规律时存在局限性，主要问题是表征参数过于简化，无法精确表达船舶到港规律的时序特征。

本文以洋山港2020年66 d内连续的VTS中心报告船舶数为统计样本，对其是否服从泊松分布或正态分布进行卡方检验（χ²检验）和柯尔莫哥洛夫-斯摩洛夫（Kolmogorov-Smirnov，K-S）检验。

1 统计分析方法

传统的船舶流到港规律统计目标是通过分析特定水域内船舶的到达时序规律，预测该水域内未来一段时间内的到港船舶数。研究的基本步骤^[9-11]为：样本采集→样本参数提取→分布假设→分布假设检验→样本分布函数拟合。例如，研究船舶到港规律时，可在收集数据的基础上，假设该数据反映船舶在不同时刻的到港数量分布符合泊松分布或正态分布，然后通过提取样本特征参数估计总体特征值或假设分布中的待定参数，建立一个完整的分布函数，进行下一步假设有效性检验。

传统的分布假设检验方法包括正态概率纸法、夏尔罗-威尔克（Shapir-Wilk，W）检验法、达戈斯提诺（D′Agostino，D）检验法、χ²检验法，K-S检验法等，本文选取χ²检验法和K-S检验法对船舶到港规律分布假设进行检验，这2种方法不受总体分布的限制，具有较强的通用性。

1.1 χ²检验

χ²检验是英国人Pearson于1900年提出的一种统计方法，也称作皮尔逊检验^[3]。该方法是将采集的样本数据按大小排序，采用特定规则界定各条数据对应的区间，将样本数据划分为m个升序区间，构建检验函数为

式中：N_i为各区间对应的试验观测样本i的观察值，n_i为对应区间概率。当数据分组数m足够大（m>>1）或N_i足够大时，统计量χ²趋于卡方分布。其分布自由度为m-r-1，r为假设分布中估计的参数个数，与m相比，当r相对较小时，自由度可近似为m-1。

计算卡方积累函数

P=（χ²|m-1），

假设其符合非完全Gamma函数统计规律，对应的Gamma互补函数

Q（χ²|m-1）=1-P =（χ²|m-1），    （2）

式中Q为验证分布的可信度假设参数。

区间假设对最终的检验结果有一定影响，当区间间隔距离符合平均分布时，拟合优度检验过程密度函数可能产生明显的拖尾；当假设区间间隔距离存在差异但各区間数据量相等时，该累积密度函数中存在的主峰值大小及其函数表征将对统计结果造成显著影响。出现以上问题时，通常进行小区间合并或截尾。

1.2 K-S检验

K-S检验主要通过计算拟合残差的方式进行样本高阶检验^[12-13]，该检验假设特定函数S_N（x）为已知分布函数（如正态分布、卡方分布等），P_N（x）为收集样本的假设分布函数，通过计算已知分布函数和假设分布函数在各连续或非连续区间的差值积累分布，并选取最大差值作为函数拟合精确表征。K-S检验的最大差值

式中N为试验数据具体数量。

如果D_obs<0.05，认为该假设通过K-S检验，样本数据服从指定分布；如果D_obs≥0.05，认为假设分布不成立。本文定义K-S检验标准为

P［D>D_obs］=Q_ks（λ） ，    （4）

2 船舶流数据处理

根据洋山港VTS的船舶报告资料，采集到2020-07-01—09-04每日到港船舶数，并将其作为船舶流概率分布研究的样本。由于数据统计齐全且样本点众多，因此将7月的549个样本点作为样本Ⅰ，8月的744个样本点作为样本Ⅱ， 9月的94个样本点作为样本Ⅲ。为分析同一水域船舶流是否具有一定特征，对3个样本分别作假设检验。船舶流强度（艘/h）特征统计如表1所示。

为研究船舶时序特征，根据到港船舶数进行船舶分组，区间间隔最低为1艘，统计该水域7～9月内到港船舶数，计算对应的船舶到港频率^[14-19]

式中：k为每h最大到港船舶数，t_i为每h到港i艘船舶所需时间。

采用式（5）进行计算，结果如图1所示。

由图1可知：该水域船舶到港存在一定规律，船舶流强度多为5～22 艘/h。7月每h到港8条船的频率最高，约为9%；8月每h船舶到港11艘的频率最高，约为10%；9月每h船舶到港13艘的频率最高，约为13%。根据图1并参照以往经验，假设船舶流服从泊松分布或正态分布，检验该水域每月到港船舶分布是否符合相应分布假设。

3 VTS报告的船舶流分析

3.1 泊松分布的假设检验

根据洋山港VTS报告的船舶流特征统计量，对到港船舶分布进行泊松分布的χ²检验和K-S检验，并在这2种假设检验中选择相对快捷的检验方法进行正态拟合。

假设到港船舶数服从泊松分布，则在数据样本基础上，该水域某1 h内出现n艘船的概率

P（n）=（φt）ⁿe^-λt/n！ ，    （6）

式中：t为间隔时间，t=1 h；φ为分布假设中估计的参数个数，一般以先验值为依据，采用极大似然估计法估计，即φ等于观测样本均值（在实践中还可将φ再放宽20％），式（6）变为

根据式（1）采用χ²检验对3个子样本进行泊松分布的假设检验，计算结果（经过截尾处理）为：

1）样本Ⅰ的χ²＝319.97，在显著水平为0.05时χ²（17-1-1）的极限值为24.996；

2）样本Ⅱ的χ²＝350.79，在显著水平为0.05时χ²（18-1-1）的极限值为26.296；

3）样本Ⅲ的χ²＝41.20，在顯著水平为0.05时χ²（10-1-1）的极限值为15.507。

3个子样本的计算结果均大于显著水平为0.05下χ²的极限值，说明在等间隔内出现的到港船舶数不符合泊松分布。采用χ²检验时，计算过程中如果理论频数n_ip_i<5（n_i为某船舶在区间i到达数量数，p_i为对应的概率），则需要合并处理，并且根据实际需要，将3个子样本都进行截尾处理^[12-17]。由于计算量较大，仅给出样本Ⅲ进行χ²检验的过程，如表2所示（加粗数值为截尾处理的结果）。

由表2可知：样本Ⅲ通过相应检验，其拟合分布模型较为可信。采用χ²检验对3个样本进行泊松分布的假设检验，计算结果分别为0.145 38、0.135 10、0.176 84，而在显著水平为0.05下样本II和样本III的检验结果分别是0.049 60、0.138 20。3个子样本计算结果均大于相应的χ²检验极限值。通过χ²检验，洋山港VTS报告船舶在等间隔内的出现规律不符合泊松分布的假设。χ²检验法易受区间及区间容量影响，对具体分布需进行特殊处理^[20-21]，难度较大，本文试验采用截尾法也不能完全消除误差，参数估计效果精确度较低^[22]。

仍以样本Ⅲ进行K-S检验为例给出计算结果，如表3所示。

由表3可知：理论上K-S检验的灵敏度较高，且不受分区间的影响。K-S检验还可采用MATLAB编程代替数据计算，检验过程快捷、简便。

3.2 基于MATLAB的正态分布假设检验

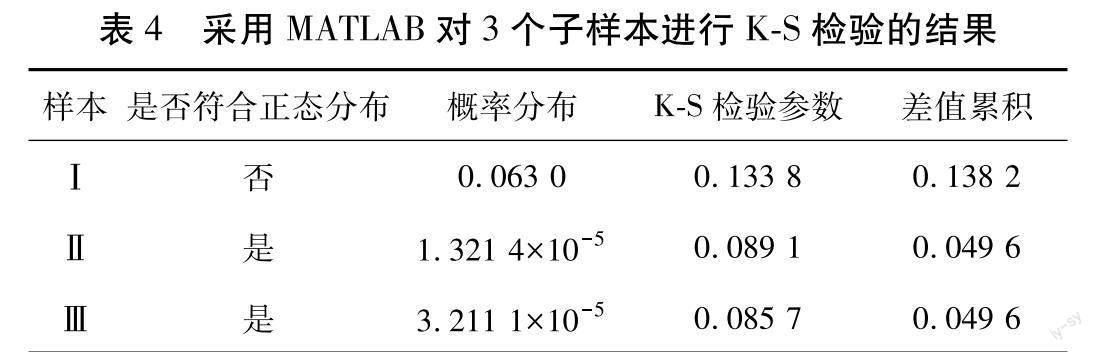
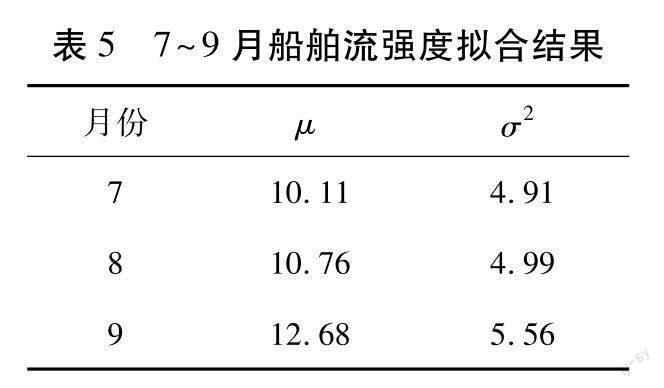
在MATLAB环境下对3个子样本的正态分布做K-S检验，具体步骤为：1）将统计的样本值给变量a赋值；2）基于mean和var命令计算统计样本均值μ和方差σ²；3）采用Kstest命令调用K-S检验函数，判断真实结果与仿真结果间差值之和是否小于0.05；4）判断该分布函数假设是否通过检验^[23-25]。收集样本的分布假设检验结果，如表4所示。由表4可知：7月真实结果与仿真结果间差值累积之和大于0.05，8、9月小于0.05。各样本船舶流强度拟合结果如表5所示。3个子样本正态分布拟合情况如图2所示。

由表4、5及图2可知：样本I的正态分布拟合结果不理想，样本II、III正态分布拟合结果通过检验。

所分析的船舶流样本是连续统计且数据可靠，但洋山港VTS监控水域船舶流空间分布复杂，存在多个报告线，并且船舶有进有出，易造成数据统计上的误差，对分析船舶流特征不利。

为减小误差，在χ²检验中合并小区间，3次χ²检验均采用截尾法。为进一步验证该水域船舶流的特征，在消除部分时间敏感数据，仅将每天07：00—21：00每h的船舶流情况作为新样本进行K-S检验，检验结果没有改变，即8、9月船舶流样本服从正态分布，7月船舶流样本不服从泊松分布和正态分布。

理论上来说，船舶流到港是随机事件，应该服从某一概率分布。本文仅对该水域的船舶流进行泊松分布和正态分布的假设检验，对交通流分布拟合还可考虑采用其他函数分布描述水域交通流分布情况，包括χ²分布、伽玛分布、对数正态分布等概率分布函数。

4 结语

对洋山港VTS报告船舶流进行统计分析，采用χ²检验和K-S检验对其概率分布进行泊松分布假设检验，检验结果表明洋山港船舶流不服从泊松分布；采用MATLAB软件对其进行正态分布假设的K-S检验，发现洋山港的船舶流正态分布特征不明显，其中8、9月部分连续数据服从正态分布。因水域特征等不同因素影响，船舶流的分布特征不一定局限于泊松分布和正态分布2种常规分布上，研究结论可为船舶流的后续研究提供借鉴和参考。

参考文献：

[1]刘敬贤，李云斌.天津港主航道船舶到达规律的统计分析[J].武汉理工大学学报（交通科学与工程版）， 2008， 32（2）：351-353.

LIU Jingxian， LI Yunbin. Distribution regularity analysis of ship arrival and deparment at the Tianjin Port main channel[J].Journal of Wuhan University of Technology （Transportation Science & Engineering）， 2008， 32（2）： 351-353.

[2]余劲，张玮，姜继红，等.西江航道船舶流的概率分布特性[J].交通运输工程学报，2006，6（2）：88-93.

YU Jin， ZHANG Wei， JIANG Jihong， et al. Probability distribution of vessel traffic flow in Xijiang waterway[J].Journal of Traffic and Transportation Engineering， 2006，6（2）：88-93.

[3]张矢宇，杨宇昊，陈尘，等.基于回归-卡尔曼滤波组合模型的航道整治区域船舶交通流时空预测[J].大连海事大学学  报，2021，47（1）：37-44.

ZHANG Shiyu， YANG Yuhao， CHEN Chen， et al. Spatio-temporal prediction of ship traffic flow in waterway regulation area based on regression-Kalman filter combination model[J]. Journal of Dalian Maritime University， 2021，47（1）：37-44.

[4]高廣旭，刘敬贤，刘奕，等.基于矩阵分解的船舶交通流预测方法研究[J].武汉理工大学学报（交通科学与工程 版），2022，46（1）：171-176.

GAO Guangxu， LIU Jingxian， LIU Yi， et al. Research on ship traffic flow prediction method based on matrix factorization[J]. Journal of of Wuhan University of Technology （Transportation Science & Engineering）， 2022，46（1）：171-176.

[5]肖建兵，惠子刚.基于改进PSO-BP神经网络的船舶交通流预测分析[J].天津航海，2020（3）：48-53.

[6]甘浪雄，张磊，邹早建，等.基于场方法的船舶交通流分析[J].上海交通大学学报，2014，48（4）：551-557.

GAN Langxiong， ZHANG Lei， ZOU Zaojian， et al. Analysis of vessel traffic flow based on field method[J].Journal of Shanghai Jiaotong University， 2014，48（4）：551-557.

[7]朱玲，江朝抒，陈祝明.KS，χ²检验方法的K分布杂波参数估计研究[J].电子科技大学学报，2008，37（增刊）：13-15.

ZHU Ling， JIANG Chaoshu， CHEN Zhuming. Parameter estimation study of K-distribution based on the goodness-of-fit test[J].Journal of University of Electronic Science and Technology of China， 2008，37（Suppl.）：13-15.

[8]吴中，王雪洁.内河航道船舶交通流研究[J].贵州大学学报（自然科学版），2014，31（1）：118-122.

WU Zhong， WANG Xuejie. Study of vessel traffic flow in inland waterway[J].Journal of Guizhou University （Natural Sciences）， 2014，31（1）：118-122.

[9]金辉，刘克中，马杰，等.基于高斯混合模型的船舶到达规律研究[J].武汉理工大学学报（交通科学与工程版），2020，44（1）： 162-166.

JIN Hui， LIU Kezhong， MA Jie， et al. Research on vessel arrival rules based on Gaussian mixture model[J].Journal of Wuhan University of Technology （Transportation Science & Engineering）， 2020，44（1）： 162-166.

[10]曹興飞，赵永涛，曹方全，等.基于ARENA的沿海港口航道通过能力仿真研究[J].中国水运（下半月）， 2017，17（12）： 96-97.

[11]吴兆麟，朱军.海上交通工程[M].大连：大连海事大学出版社，2004.

[12]盛骤，谢式千，潘承毅.概率论与数理统计[M].5版.北京：高等教育出版社，2020.

[13]廖鹏，张玮.船闸日到船概率分布参数估计[J].交通运输工程学报，2004，4（2）：115-118.

LIAO Peng， ZHANG Wei. Parameter estimation on daily arrival distribution of waterway lock[J].Journal of Traffic and Transportation Engineering， 2004，4（2）：115-118.

[14]杨星，王晶尧， 刘克中，等.基于船舶减速的单线航道通航效率评价[J].中国航海，2020，43（1）：35-39.

YANG Xing， WANG Jingyao， LIU Kezhong， et al. Evaluation of navigation efficiency of single-lane channel from the angle of reduced ship speed[J].Navigation of China， 2020，43（1）：35-39.

[15]廖鹏.内河船舶交通流量的时空分布特征[J].水利水运工程学报，2009（2）：33-38.

LIAO Peng. Temporal and spatial distribution of traffic flow in inland waterways[J].Hydro-Science and Engineering， 2009（2）：33-38.

[16]YU Jingjing， TANG Guolei， SONG Xiangqun，et al. Ship arrival prediction and its value on daily container terminal operation[J].Ocean Engineering，2018（157）：73-86.

[17]刘钊，崔珑献，李岩，等.基于二维矩阵分解的船舶交通流预测[J].中国航海，2021，44（3）：76-83.

LIU Zhao， CUI Longxian， LI Yan， et al. Ship traffic flow prediction with bidimensional matrix mode decomposition[J].Navigation of China， 2021，44（3）：76-83.

[18]梅妍玭，张得才，傅荣.一种准确预测船舶交通流的自适应遗传算法优化的BP神经网络模型研究[J].电子器件，2020， 43（2）： 452-455.

MEI Yanpin， ZHANG Decai， FU Rong. A BP neural network model for adaptive genetic algorithm optimization for predicting ship traffic flow[J].Chinese Journal of Electron Devices， 2020， 43（2）： 452-455.

[19]冯宏祥，肖英杰，孔凡邨.基于支持向量机的船舶交通流量预测模型[J].中国航海，2011，34（4）：62-66.

FENG Hongxiang， XIAO Yingjie， KONG Fancun. Study of vessel traffic forecasting model based on support vector machine[J].Navigation of China， 2011，34（4）：62-66.

[20]刘钊，刘敬贤，周锋，等.船舶交通流行为特征及其在海上交通组织中的应用[J].大连海事大学学报，2014，40（2）：22-26.

LIU Zhao， LIU Jingxian， ZHOU Feng， et al. Behavior characteristics of vessel traffic flow and its realization in marine traffic organization[J].Journal of Dalian Maritime University， 2014，40（2）：22-26.

[21]吴康，汪洋，谢磊，等.基于状态空间的连续断面船舶交通流量预测研究[J].交通信息与安全，2015（2）：51-56.

WU Kang， WANG Yang， XIE Lei， et al. A study of vessel traffic flow forecast based on state space analysis of continuous cross sections[J].Journal of Transport Information and Safety，2015（2）：51-56.

[22]王群朋，范天佑.基于SPSS和多元线性回归的船舶交通流分布拟合研究[J].广州航海学院学报， 2018，26（2）：29-32.

WANG Qunpeng， FAN Tianyou. Distribution fitting of vessel traffic flow based on SPSS and multivariate linear regression[J].Journal of Guangzhou Maritime University， 2018，26（2）：29-32.

[23]柯冉绚，胡栩祯，陈毅.基于IWRAP模型的船舶交通流数据拟合模型[J].中国航海，2018，41（4）：77-82.

KE Ranxuan， HU Xuzhen， CHEN Yi. Ship traffic flow data prosessing for IWRAP[J].Navigation of China， 2018，41（4）：77-82.

[24]周薇，许洁，王想实.基于大数据分析的船舶交通特征统计分析[J].舰船科学技术，2019，41（4A）：82-84.

ZHOU Wei， XU Jie， WANG Xiangshi. Statistical analysis of ship traffic characteristics based on big data analysis[J].Ship Science and Technology， 2019，41（4A）：82-84.

[25]劉成勇，万伟强，陈蜀喆，等.基于灰色马尔科夫模型的船舶交通流预测[J].中国航海，2018，41（3）：95-100.

LIU Chengyong， WAN Weiqiang， CHEN Shuzhe， et al. Prediction of vessel traffic flow based on grey Markov model[J].Navigation of China， 2018，41（3）：95-100.

Statistical characteristics of vessel flow in VTS reports in Yangshan Port

LIU Chao

Department of Navgation，Anhui Communications Vocational & Technical College，Hefei 230051，China

Abstract：In order to analyze the characteristics and operation rules of ship flow in a certain water area， and research quantitatively the rules of ship flow to the port， and provide data support for port operation and vessel traffic services （VTS）， parameter estimation of ship arrival from the perspective of optimal fitting based on the K-S test and χ²test of moment estimation theory is carried out， taking 1387 consecutive VTS measured ship flow records in Yangshan Port water area in 66 days in 2020 as the statistical samples. The results show that the ship flow samples reported by VTS in Yangshan Port waters in August and September obey Normal distribution， while the samples in July do not obey Poisson distribution and Normal distribution， which proves that the distribution characteristics of ship flow change significantly with environmental and time factors， and only Poisson distribution or Normal distribution can′t fully describe the characteristics of traffic flow in waters. The relevant research conclusions can provide reference for the analysis of ship flow characteristics， navigation scheduling and other related research.

Keywords：normal distribution; Poisson distribution；K-S test；χ²test；ship flow

（责任编辑：王惠）