深厚覆盖层地区土层地震反应的不确定性分析
叶迎晨


摘要以上海地区作为深厚覆盖层地区代表,在丰富的地质资料基础上,全面、系统地分析了100 m 以深地层的土层分布、剪切波速、土动力特性参数、密度和地震输入界面这5个不确定因素可能的分布范围,并采用逻辑树分析方法,利用等效线性化土层地震反应分析,计算得到了这5种不确定因素在23种工况下3个超越概率、4个典型地质孔的地表峰值加速度和反应谱结果。经分析表明,100 m 以深地层的土动力特性参数、剪切波速、土层分布、密度属于低敏感性因素,其不确定性对地表地震动参数影响较小,峰值加速度差异基本在5%以内;地震输入界面属于高敏感性参数,对地表地震动参数(尤其是低频段)影响较大,最大差异可达30%—40%。地震安全性评价工作中应合理设定地震输入界面,以避免可能对工程抗震设防参数带来的不利影响。
关键词深厚覆盖层地区;深部地层不确定性;土层地震反应;地震动参数
中图分类号: P315.9文献标识码: A文章编号:2096-7780(2023)05-0193-10
doi:10.19987/j.dzkxjz.2023-011
Uncertainty analysis of seismic response of soil layerin deep overburden area
Ye Yingchen
(Shanghai Yuchen Engineering Technology Co., Ltd., Shanghai 201108, China)
AbstractTaking Shanghai area as the representative of deep overburden area,based on abundant geological data, this paper comprehensively and systematically analyzes the possible distribution range of 5 uncertain factors,includingsoil layer distribution,shear wave velocity,soil dynamic characteristic parameters,density and seismic input interface, in a depth of 100 m,and uses the logic tree analysis method and equivalent linear method for seismic response analysis ofsoil layers,the surface peak acceleration and response spectrum results of 5 uncertain factors,3 exceedance probabilitiesand 4 typical geological holes under 23 working conditions are calculated. It shows that the parameters of soil dynamiccharacteristics,shearwavevelocity,soillayerdistributionanddensityinthedepthof 100 marelowsensitive parameters,and their uncertainty have little impact on the ground motion parameters,the difference of peak acceleration are basically within 5%. The seismic input interface is a highly sensitive parameter,which has a great impact on the ground motion parameters (especially to the low frequency band),with the maximum difference of 30%—40%. The seismic input interface should be reasonably set in the seismic safety evaluation to avoid the adverse impact on the seismic fortification parameters of the project.
Keywords deepoverburdenarea; deepstratumuncertainty; seismicresponseofsoillayer; groundmotionparameters
引言
土層地震反应分析是工程场地地震安全性评价工作中重要环节之一,其结果的合理性对工程结构抗震设防十分重要。根据地震安评规范[1]中有关工程场地勘测的规定,Ⅱ级工作中控制孔深度超过100 m 时,剪切波速仍小于500 m/s,可终孔。对于深厚覆盖层地区(如上海、江苏沿海城市等),基岩埋深一般大于100 m 甚至千余米,100 m 深度以浅的地层主要以第四纪松散沉积物为主。大量的工程经验显示,该类土层在100 m深度处的剪切波速可能达不到500 m/s。因此,深厚覆盖层地区的Ⅱ级地震安评工作钻孔勘测深度一般设定在100 m左右。
对于深厚覆盖层场地,土层地震反应分析的不确定性根据模型参数的来源可划分为已知参数的不确定性和未知参数的不确定性。已知参数的不确定性分布于勘测深度范围,主要受工作量、仪器、试验条件等限制,如输入随机地震动时程的条数、土层剪切波速测试间隔、土动力试验样品取样数量、剪切波速测试仪和土动力试验仪的精度,以及剪切波速测试过程中钻孔对地层的扰动、钻探取样和样品制备过程对原状土层状态的扰动等。未知参数的不确定性则源于100 m 以深至地震输入界面深度范围土层模型参数的未知性。
对于已知参数的不确定性分析,已有研究较多。石玉成等[2]针对基岩地震动输入、计算模型、场地介质参数的不确定性对场地地震反应分析的影响进行了研究;楼梦麟等[3]研究了上海软土的动力参数变异性对土层地震反应的影响;冯伟栋等[4]采用等效线性化方法分析了土层剪切波速、输入界面、分层等参数变异性对场地地表地震动的影响。相关标准、规定等对地震安评工作中已知参数给出了较为明确的要求,如输入地震动时程条数不少于3条、剪切波速测试间距不大于1 m、典型土样采样间距要求等,在严格按规定开展地震安评工作的条件下,其结果的精确度基本可满足工程应用的需求。而对于未知参数不确定性分析的相关研究则较少,已有的研究主要集中于地震输入界面对场地地震动的影响,如洪海春等[5]对江苏盐城地区100 m 深度处剪切波速仍小于500 m/s 的情况,研究了地震输入界面位置的不确定性对地震反应的影响;深部地层各因素的不确定性分析尚缺乏全面、系统的研究。
相关标准、规定等对100 m 以深至地震输入界面范围的土层模型如何确定未给出明确要求。目前,地震安评工作中一般处理方式为参考邻近的基岩孔或物探资料确定基岩埋深、土层性质及层位,采用深孔波速资料拟合或者浅部实测波速拟合外推的方式获取深部剪切波速资料,参考类似土性的土动力试验参数和密度参数确定等。然而,不论采用何种方式,其结果的合理性和准确性仍有待商榷,进而可能对工程的地震安全性产生影响。因此,全面、系统地研究深部地层参数不确定性对场地地表地震动参数的影响在地震安评工作中有着迫切需要。
本文以上海地区作为深厚覆盖层地区代表,通过分析深部地层的不确定因素可能的变化范围,研究各因素的不确定性对地表地震动参数的影响,为地震安评工作提供参考。
1 不确定性分析方法
目前土层地震反应分析主要采用的方法为等效线性化波动方法( Equivalent Linear Method,EQLM),该方法假设剪切波从黏弹性半无限基岩空间垂直入射到水平层非线性土体中,并向上传播,根据波传播理论,利用傅氏变换法结合土体非线性特性的复阻尼模量及等效线性化处理方法可以计算出场地介质的动力反应值[6]。根据波动理论及复阻尼理论可知,每一土层中介质运动必须满足波动方程:
式中,U为土层中介质反应的位移值;ρ为土层中介质的密度;G为介质的动力复剪切模量,与动剪切模量、阻尼比和剪切应变有关。
土层地震反应分析中深部地层的不确定因素有多种,完整的地层模型参数包括土层分布、土动力特性参数、剪切波速、密度和地震输入界面5个。
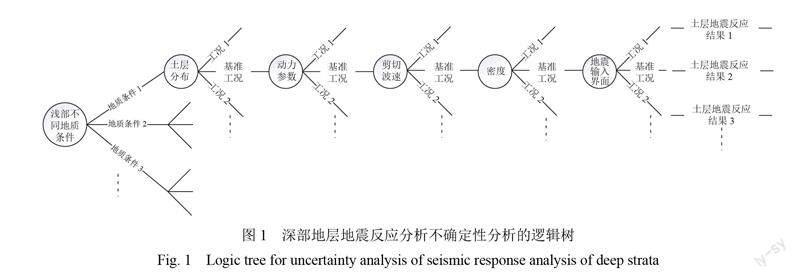
逻辑树方法是表达各环节参数的不确定性的有效工具,逻辑树上的节点代表不同的不确定因素,分支代表该因素可能分布的范围,地震危险性分析中常采用该方法来开展不确定性分析[7-9]。因此,本文采用逻辑树方法,将5个因素列入逻辑树节点中,各节点之间相互独立,单独分析每个节点不同分支的终端结果的敏感性并进行对比,进而得出不同因素的不确定性影响程度。因本文分析的对象为地层模型中100 m 以深的部分,而不同类型的浅部地层可能产生不同的研究结果,为增加分析结果的代表性,本次同时对各种不同浅部地质条件下的地层模型开展分析。图1为本文分析所用的逻辑树示意图。
2 不确定因素范围分析
本文研究的关键和难点在于如何確定深部地层这5个参数可能的变化范围,并在此基础上分析参数不确定性对地表地震动参数的影响。
上海作为典型的深厚覆盖层地区,开展了大量的地质勘探和地震安评工作,有着丰富的地质钻孔、剪切波速、土层物理力学参数和土动力参数资料,深孔资料亦分布广泛。这些资料覆盖面广、代表性强,在此基础上开展本项研究可靠性高。
2.1 土层分布
根据深孔资料[10]分析可知,上海地区覆盖土层厚度一般在200—300 m 范围内,基岩埋深呈现出由西向东、由南向北逐渐增大的趋势;100 m 以深土层主要以黏土、粉质黏土、粉砂、细砂、粗砂为主,局部为砂质粉土;按土性大致可分为黏性土和砂土两大类,其中黏性土状态一般为可塑—硬塑,砂土状态一般为密实,交替分布,局部呈互层状;100 m 以深地层在上海西部地区以黏性土为主,东部地区以砂土为主。因此,100 m 以深至地震输入界面范围内的土层分布在全部黏性土—全部砂土范围内,可细分为3种工况:工况1(全部黏性土)、工况2(黏性土与砂土交替分布)和工况3(全部砂土)。
2.2 土动力特性参数
由于100 m 以深土层的土动力特性参数试验研究成果很少,工程应用中一般采用参考100 m 以浅同类土层参数的方法,其不确定性在于土层埋深可能产生的影响。理论分析可知,随着深度的增大,土体受到的围压随之增大,土体更加紧密,对应的剪切模量比增大、阻尼比减小,其不确定之处在于土动力特性参数随深度变化的幅度大小。
张亚军等[11]曾对上海地区土层按标准层进行了动剪切模量比和阻尼比的统计研究,利用数百个土样的共振柱/动三轴试验结果,通过模型拟合的方式给出了上海地区②—⑨层土的土动力特性参数,该结果对上海地区土层具有较高的代表性,表1为土层分类及土动力特性参数特征。
从表1可以看出,黏性土中⑤4层粉质黏土的动剪切模量比最大、阻尼比最小,该层为古河道沉积地层,与⑥层粉质黏土土性类似,但埋深较大,对应的模量参数较大;砂土中埋深最大的⑨2层中粗砂的动剪切模量比最大、阻尼比最小。因此,按“土性类似、深度就近”的原则,100 m 深度处黏性土采用⑤4层可塑—硬塑状粉质黏土的土动力特性参数,砂土采用⑨2层密实状中粗砂的土动力特性参数。
参考100 m 以浅土层参数随深度变化的幅度,通过类比的方法确定100 m 以深土层动力特性参数的变化范围。根据张亚军等[11]的研究成果,黏性土在2—50 m 深度范围内动剪切模量比变化范围为1.0—1.7,阻尼比变化范围为0.7—0.9;砂土在5—100 m 深度范围内动剪切模量比变化范围为1.0—1.3,阻尼比变化范围为0.5—0.7。进而确定200 m 深度处黏性土和砂土动剪切模量比变化幅度相对于100 m 深度处分别为1.0—2.0和1.0—1.6,阻尼比变化幅度分别为0.5—0.7和0.4—0.6。100—200 m 以及200 m 以深部分土动力特性参数按深度插值获得。
实际分析时,100 m 深度处土层的土动力特性参数采用浅部类似土层的参数,200 m 深度处土层的土动力特性参数采用100 m 处的参数按类比的比值确定,以此为基准工况,考虑一定的变化范围,按?50%—+100%的范围设置了5种工况条件(图2),200 m 深度处土动力特性参数变化分别为:
●工况4:动剪切模量比?50%,阻尼比+100%;
●工况5:动剪切模量比?25%,阻尼比+50%;
●工况6:动剪切模量比和阻尼比均为基准值;
●工况7:动剪切模量比+50%,阻尼比?25%;
●工况8:动剪切模量比+100%,阻尼比?50%。
2.3 剪切波速
大量学者对剪切波速与深度之间的关系开展了深入研究[12-15],从研究成果中可以看出,剪切波速与深度有显著的相关性,基本上呈现出随深度增大而增大的趋势,各学者研究方法的区别主要在于采用何种经验模型,通常包括线性函数、多项式函数、幂函数、幂函数+常数函数等。然而,不论采用何种经验模型,剪切波速随深度的变化幅度均呈现出随深度增加而逐渐减小的态势,在100 m 以深时则近似呈线性。因此,本文对100 m 深度至地震输入界面范围的剪切波速采用线性模型,其中100 m 处剪切波速取实测均值,地震输入界面处剪切波速取经验值并考虑其不确定性。
根据上海地区已有的实测深孔波速资料经验拟合公式,选取地震输入界面代表性深度280 m,计算得到该深度处剪切波速为585 m/s 左右;上海地区已开展的大量地震安评波速测试结果显示,100 m 处剪切波速主要范围为400—450 m/s,将实测波速与深孔波速拟合公式进行衔接调整后,280 m 处剪切波速范围为620—670 m/s。根据以上分析结果,考虑深度280 m 处剪切波速的不确定性,本次研究取550—700 m/s 范围进行分析,细分工况为4种(图3):
●工况9:深度280 m 处,波速550 m/s;
●工况10:深度280 m 处,波速600 m/s;
●工况11:深度280 m 处,波速650 m/s;
●工况12:深度280 m 处,波速700 m/s。
2.4 密度
密度资料相较于土动力特性参数和剪切波速资料更加丰富,工程地质勘察工作一般均涉及大量土样的密度试验。100 m 以浅地层的密度在上海市勘察规范[16]中给出了统计范围;随着大量超高层项目的建设,100 m 以深地层在勘察工作中亦开展了大量土工试验[10],勘察深度最深可达290 m。经收集、整理这些密度资料,统计分析后得到:深度50—100 m 范围,黏性土密度在1.90—2.10 g/cm3范围内,砂土密度在1.81—2.16 g/cm3范围内;深度100—290 m 范围,黏性土密度在1.94—2.09 g/cm3范围内,砂土密度在1.90—2.19 g/cm3范围内。从统计结果可以看出,土层密度随深度的变化较小,可基本确定100 m 以深的黏性土密度可能在1.9—2.1 g/cm3范围内,砂土密度可能在1.8—2.2 g/cm3范围内。细分密度工况为5种:
●工况13:黏性土密度1.90 g/cm3,砂土密度1.80 g/cm3;
●工况14:黏性土密度1.95 g/cm3,砂土密度1.90 g/cm3;
●工况15:黏性土密度2.00 g/cm3,砂土密度2.00 g/cm3;
●工况16:黏性土密度2.05 g/cm3,砂土密度2.10 g/cm3;
●工况17:黏性土密度2.10 g/cm3,砂土密度2.20 g/cm3。
2.5 地震输入界面
对于深厚覆盖层地区,地震安评规范[1]规定 II 级工作地震输入界面应采用剪切波速不小于500 m/s 的土层顶面。实际工作中对于地震输入界面的选取不尽相同。上海地区一般采用基岩钻孔资料确定基岩面埋深,以基岩面作为地震输入界面,基岩剪切波速采用800 m/s;其他地区有以剪切波速500 m/s 或550 m/s 作为地震输入界面的,这些地震输入界面选取方法均符合规范要求。经综合考虑,本文中地震输入界面确定方法要求:①基岩面;②剪切波速为500—700 m/s 的土层深度顶面。对应的工况可细分为6种:
●工况18:基岩深度(剪切波速800 m/s);
●工况19:剪切波速500 m/s 深度;
●工况20:剪切波速550 m/s 深度;
●工况21:剪切波速600 m/s 深度;
●工况22:剪切波速650 m/s 深度;
●工况23:剪切波速700 m/s 深度。
3 计算模型的确定
上海地区工程地质条件有明显的分区特点,有正常沉积地层区、古河道地层区,有的浅部以粉性土为主、有的浅部以淤泥质土为主、有的浅部以硬土层为主的地质条件,也有Ⅲ类和Ⅳ类场地等地质条件,这些基本上代表了深厚覆盖层地区的各种地层分布情况。
本文研究以地层参数为重点分析对象,为考虑不同地质条件可能存在的影响,选取了4种典型地层条件下的钻孔模型开展不确定性分析,分别为:①湖沼平原地区暗绿色硬土层分布较浅的地层,浅部土层土质较硬,一般属Ⅲ类场地;②滨海平原地区正常地层,浅部有厚层淤泥质土;③滨海平原地区古河道地层,古河道切割深度大,分布有厚层的黏性土;④河口、砂嘴、砂岛地区浅部粉性土分布地层。这4种典型地层钻孔模型的100 m 以淺地层采用实际钻探成果,100 m 以深地层在基准工况情况下参考邻近的基岩地质孔成果[10],其地层剖面分布如图4 所示。
计算模型中0—100 m 深度范围地层参数为实测值或实测统计值,100 m 以深范围的地层参数分以上23种工况进行分析,其中基准工况为:土层分布参照邻近深孔地层,即黏性土与砂土交替分布;土动力特性参数为100 m 处采用浅部同类土层的参数,200 m 深度处土层的土动力特性参数采用100 m 处的参数按类比的比值确定,其余深度按插值确定;剪切波速采用280 m 波速中间值625m/s;密度采用统计中值,即黏性土密度2 g/cm3和砂土密度2 g/cm3;地震输入界面采用基岩面,基岩剪切波速为800 m/s。不确定分析时仅对100 m 以深地层的单个参数进行调整,其他参数采用基准工况。
4 土层地震反应分析计算
考虑不同地震动输入幅值和随机时程数量可能存在的影响,本文采用3个超越概率、每个超越概率6条时程的方案,每个工况每个地层模型输入时程样本数量为18条。
基岩地震动输入采用上海地区所在区域的五代图潜在震源区划分方案和五代图对应的东部活跃区地震动衰减关系计算得到的基岩反应谱(超越概率50年63%的 PGA 为22.2 cm/s2、50年10%的 PGA 为75.9 cm/s2、50年2%的 PGA 为145.1 cm/s2,主要受近场地震影响),利用三角级数叠加法合成基岩地震加速度时程。
以此为地震动输入值,采用土层地震反应等效线性化分析方法,计算得到的23个工况、4种典型地层的地表峰值加速度和周期1.0 s处反应譜结果见图5和图6。
图7为5个地层参数在不同工况下,不同周期处(0 s、0.1 s、0.3 s、0.5 s、1.0 s、1.5 s、1.9 s、2.5 s、3.1 s、5.0 s)反应谱结果与基准工况偏差的绝对百分比分布情况。
图8为选取的典型地层2在50年超越概率10%条件下计算结果中不同周期的反应谱偏差随周期的变化曲线,以及不同地震输入界面工况下反应谱曲线对比。
5 结果分析
从图5和图6可以看出,不同超越概率条件下各工况对地表峰值加速度和反应谱的影响规律基本一致。
从图7和图8可以看出,不同地震动输入情况下的峰值加速度和反应谱值结果变化情况差别较小,不同地层模型参数的变化对地表峰值加速度和反应谱的影响以及不同周期处的反应谱影响有较大差异。
从图5—图8的分析中可得到如下结果:
(1)土层分布不确定性对地表地震动影响小,PGA 偏差基本在3.5%以内,砂土对地表峰值加速度影响为正,黏性土影响为负(图5),对周期1.0 s处反应谱值影响很小,无明显趋势(图6);土层分布对地表反应谱高频段影响比低频段大,主要影响范围在0—0.4 s,影响峰值点在0.1—0.13 s 左右,在周期2.8 s 之后影响很小(图7和图8a)。
(2)土动力特性参数不确定性对地表地震动影响较小,PGA偏差基本在4.8%以内,高动剪切模量比、低阻尼比对地表峰值加速度影响为正,低动剪切模量比、高阻尼影响为负(图5),对周期1.0 s处反应谱值影响很小,无明显趋势(图6);土动力特性参数对地表反应谱高频段影响比低频段大,主要影响范围在0—0.4 s,影响峰值点在0.1—0.13 s 左右,在周期2.8 s 之后影响很小(图7和图8b)。土动力特性参数与土层分布对地表反应谱的影响基本一致。
(3)剪切波速不确定性对地表地震动影响小,PGA 偏差基本在3.5%以内,深部剪切波速高时对地表峰值加速度影响为正,深部剪切波速低时影响为负(图5),对周期1.0 s处反应谱值影响小,影响趋势无规律(图6);剪切波速对地表反应谱整体均有影响,对低频段的影响比高频段稍大(图7和图8c)。
(4)密度不确定性对地表地震动影响很小,PGA 偏差基本在1.5%以内,高密度对地表峰值加速度影响为正,低密度影响为负(图5),对周期1.0 s处反应谱值影响很小,无明显趋势(图6);密度对地表反应谱低频段影响比高频段大,主要影响范围在1—4 s 左右,影响峰值点在1.5 s左右(图7和图8d)。
(5)不同地震输入界面对地表地震动影响较大, PGA 偏差最大可达15.7%,地震输入界面对应剪切波速高对地表峰值加速度影响为正,剪切波速低影响为负(图5),对周期1.0 s 处反应谱值影响与 PGA 一致(图6);不同地震输入界面对地表反应谱低频段影响比高频段大,偏差最大可达30%—40%,主要影响范围在0.3—5 s 左右,影响峰值点在2.2 s 左右(图7、图8e 和图8f)。
6 结论
本文以上海地区作为深厚覆盖层地区代表,采用逻辑树的方法分析了土层地震反应分析中100 m 以深地层模型参数不确定性对地表地震动参数的影响,得到如下结论:
(1)地震输入界面的剪切波速设定越高和深部地层的高动剪切模量比及低阻尼比、高剪切波速、砂性土分布多、密度高,这些工况条件对地表峰值加速度影响为正,反之为负。
(2)100 m 以深地层各因素对地表地震动参数影响程度由大到小依次为:地震输入界面、土动力特性参数、剪切波速、土层分布、密度。
(3)100 m 以深地层的土动力特性参数、剪切波速、土层分布、密度不确定性对地表地震动参数影响较小,产生的峰值加速度差异基本在5%以内,属低敏感性参数;不同地震输入界面对地表地震动参数影响较大,尤其对反应谱长周期段,产生的差异最大可达30%—40%,属高敏感性参数。
(4)深部地层的土层分布、土动力特性参数变化对地表反应谱高频段较为敏感;剪切波速和密度变化对地表反应谱整体均有影响,在低频段影响偏大;不同地震输入界面对地表反应谱低频段影响较大。
(5)在深厚覆盖层地区地震安全性评价工作中,地震输入界面的选取属于高敏感性参数,应合理设定地震输入界面,以避免可能对工程抗震设防参数带来的不利影响。
参考文献
[1]全国地震标准化技术委员会.工程场地地震安全性评价:GB17741—2005[S].北京:全国标准信息公共服务平台,2005
National Technical Committee for Seismic Standardization. Evaluation of seismic safety for engineering sites:GB17741—2005[S]. Beijing:National Public Service Platform for Standards Information,2005
[2]石玉成,蔡红卫,徐晖平.场地地震反应分析中的不确定性及其处理方法[J].西北地震学报,1999,21(3):242-246
Shi Y C,Cai H W,Xu H P. Uncertainties in site earthquake response and way of its processing[J]. Northwestern Seismological Journal,1999,21(3):242-246
[3]楼梦麟,严国香,沈建文,等.上海软土动力参数变异性对土层地震反应的影响[J].岩土力学,2004,25(9):1368-1372
Lou M L,Yan G X,Shen J W,et al. Effect of variability of dynamic parameters of soft soil in Shanghai region on seismic response of layered soil[J]. Rock and Soil Mechanics,2004,25(9):1368-1372
[4]馮伟栋,曹均锋,彭刘亚,等.土层模型参数变异性对场地地表地震动的影响分析[J].防灾科技学院学报,2020,22(3):28-34
Feng W D,Cao J F,Peng L Y,et al. Analysis of influence of soil model parameter variability on ground motion response[J]. Journal of Institute of Disaster Prevention,2020,22(3):28-34
[5]洪海春,许汉刚,陶小三,等.控制性深孔地震输入界面位置的确定方法和影响研究[J].震灾防御技术,2013,8(1):52-61
Hong H C,Xu H G,Tao X S,et al. Determination and effect of earthquake input interface of deep governing holes[J]. Technology for Earthquake Disaster Prevention,2013,8(1):52-61
[6]胡聿贤.地震安全性评价技术教程[M].北京:地震出版社,1999
Hu Y X. Technical tutorial on seismic safety evaluation[M]. Beijing:Seismological Press,1999
[7]陈汉尧,胡聿贤.地震危险性不确定性分析中专家意见的合理综合[J].华北地震科学,1993,11(3):1-8
Chen H Y,Hu Y X. Arational comprehension of experts opinions in analysis of uncertainty of seismic risk[J]. North China Earthquake Sciences,1993,11(3):1-8
[8]杨智娴,张培震,郑月君.用逻辑树方法估计地震年发生率的不确定性[J].地震学报,1998,20(2):185-193
Yang Z X,Zhang P Z,Zheng Y J. Uncertainty of estimating the annual occurrence rate of earthquakes using the logic tree method[J]. Acta SeismologicaSinica,1998,20(2):185-193
[9]章在墉.地震危险性分析及其应用[M].上海:同济大学出版社,1996
Zhang Z Y. Seismic risk analysis and its application[M]. Shanghai:Tongji University Press,1996
[10]上海市地质资料馆.上海地质资料信息共享平台[DB/OL].[2023-02-12]. https://data.sigs.cn/
Shanghai Geological Data Center. Shanghai geological data information sharing platform[DB/OL].[2023-02-12]. https://data.sigs.cn/
[11]张亚军,兰宏亮,崔永高.上海地区土动剪切模量比和阻尼比的统计研究[J].世界地震工程,2010,26(2):171-175
Zhang Y J,Lan H L,Cui Y G. Statistical studies on shear modulus ratio and damping ratios of soil in Shanghai area[J]. World Earthquake Engineering,2010,26(2):171-175
[12]李敏,杨立国,陈海鹏,等.杭州市典型土层剪切波速与埋深间的关系分析[J].震灾防御技术,2020,15(1):77-88
Li M,Yang L G,Chen H P,et al. Relationship between shear wave velocity and soil depth of typical soil layers in Hangzhou area[J]. Technology for Earthquake Disaster Prevention,2020,15(1):77-88
[13]刘红帅,郑桐,齐文浩,等.常规土类剪切波速与埋深的关系分析[J].岩土工程学报,2010,32(7):1142-1149
Liu H S,Zheng T,Qi W H,et al. Relationship between shear wave velocity and depth of conventional soils[J]. Chinese Journal of Geotechnical Engineering,2010,32(7):1142-1149
[14]战吉艳,陈国兴,刘建达,等.苏州城区深软场地土剪切波速与土层深度的经验关系[J].世界地震工程,2009,25(2):11-17
Zhan J Y,Chen G X,Liu J D,et al. Empirical relationship between shear wave velocity and soil depth on deep soft sites in urban area of Suzhou city[J]. World Earthquake Engineering,2009,25(2):11-17
[15]榮绵水,吕悦军,蒋其峰,等.渤海常见土类剪切波速与埋深关系分析[J].震灾防御技术,2017,12(2):288-297
Rong M S,Lü Y J,Jiang Q F,et al. Relationship between shear wave velocity and depth for conventional soils in the Bohai sea area[J]. Technology for Earthquake Disaster Prevention,2017,12(2):288-297
[16]岩土工程勘察规范:GB50021—2001[S].郑州:黄河水利出版社,2002
Code for investigation of geotechnical engineering:GB50021—2001[S]. Zhengzhou:Yellow River Water Conservancy Publishing House,2002

