湘西土家族苗族自治州马尾松树高-胸径混合效应模型构建

黄 靓，卢 侃，易 烜，朱晋梅，王琢玙，刘文剑

（1.湖南省青羊湖国有林场，湖南 宁乡 410627； 2.湖南省林业局，湖南 长沙 410007）

树高和胸径是森林资源调查过程中最重要的两个变量和常用的测量指标，它们在描述林分结构、评价林地生产潜力以及估算林分蓄积量、生物量的过程中，发挥了至关重要的作用［1］。胸径通常可用围尺等测量工具直接测量，而树高的测量在较为郁闭的林分中受视觉影响较大，导致测量误差较大［2］。尽管采用高精度的测量仪器（如激光、超声波测高器等）能减小树高测量误差，但对于大区域、大面积测量来说仍然费时费力，测量成本过高［3］。因此，估计林分或林木高度的最常用方法是测量其子样本，以子样本为基础，构建一个树高-胸径模型来估计它们的高度。

传统的树高-胸径模型构建往往采用普通最小二乘法，但最小二乘法通常要考虑样本的独立性假设，即独立、等方差、正态分布［4-5］。然而，林分生长数据一般具有层次结构、重复测量等特点，表现为数据之间存在异方差和自相关，不满足普通最小二乘法拟合回归模型的独立性假设［5］。同时，林木的生长通常受到树种本身特性以及复杂的生境条件影响，如区域、样地、林分条件、立地条件以及干扰等，很多学者在构建树高-胸径模型时，通过在模型中引入这些除胸径以外的变量来提高树高-胸径模型的精度与适用性［1，6-9］。混合效应模型作为处理多层次重复测量数据的有力工具，已广泛应用于树高-胸径模型等林业生长模型的构建，它既可以基于固定效应参数预估树高的平均变化趋势，又能够以随机效应参数来反映不同区域、样地以及立地条件间的树高曲线变化。Crecente-Campo等［10］以西班牙北部蓝桉（Eucalyptus globulus）林分为研究对象，构建了广义的树高-胸径混合效应模型，发现这些模型解释了83%的观测变异，且平均误差小于2.5 m。樊伟等［8］考虑到样地水平的随机效应，构建了大别山地区杉木（Cunninghamia lanceolata）树高-胸径混合效应模型，发现混合效应模型拟合效果优于基础模型以及含林分变量的模型。Ciceu等［1］基于雷泰扎特国家公园178个固定样地欧洲云杉（Picea abies）异龄林数据，考虑了描述林分结构、物种混交和竞争的23个林分变量，利用其中3个林分预测因子构建了一个广义的树高-胸径混合效应模型，能够较为精确地预测该地区挪威云杉的树高。

马尾松（Pinusmassoniana）是我国的主要用材树种之一，其分布范围广泛，其资源在我国森林资源总量中占有重要比重。根据第九次全国森林资源清查结果，马尾松林面积和蓄积分别占我国乔木林面积和蓄积的4.47%和3.67%，在水源涵养、碳增汇以及用材方面有着至关重要的地位［11］。为精确估算湘西土家族苗族自治州马尾松林树高，本研究以现有调查的湘西土家族苗族自治州8个县（市）马尾松林调查数据为基础，拟构建含区域、龄组以及立地条件中显著影响因子的树高-胸径混合效应模型，为找到适用于湘西土家族苗族自治州马尾松林树高-胸径模型提供理论依据。

1 研究区概况

研究区位于湘西土家族苗族自治州，地理坐标为109°10＇-110°23＇E、27°44＇-29°38＇N，地处云贵高原东侧的武陵山区，地势东南低、西北高，海拔97.1～1 736 m。属于亚热带季风湿润气候，冬季比较寒冷，夏季温高湿重，春夏之交阴湿多雨，年平均温度在16.0～17.0℃之间，年平均降水量为1 284.2～1 416.9mm，降雨主要集中在每年4-9月。主要土壤有黄红壤、山地黄壤、山地黄棕壤、草甸土、石灰土、酸性紫色土、碱性紫色土，全州大部分土壤呈微酸性至中性，过酸或过碱性土壤不多。森林覆盖率为70.24%，森林资源丰富，但林种较为单一，山地植被的丰富度不够，以杉、松为主的针叶纯林面积占乔木林面积的56%，生态功能较强的阔叶林、混交林、复层林只占32%。

2 材料与方法

2.1 数据来源

数据来源于湘西土家族苗族自治州2019年7-8月调查的马尾松人工林数据。数据采集于湘西土家族苗族自治州的保靖县、凤凰县、古丈县、花垣县、吉首市、龙山县、泸溪县和永顺县8个县（市），共77个样地，样地大小为25 m×25 m。在样地中选取3株标准木，用激光测高测距仪测量树高，用围尺测量胸径，最后取各样地3株标准木树高、胸径的平均值分别作为林分平均高、林分平均胸径。采用三倍标准差法剔除异常数据后为71株马尾松林分平均木。除了林分平均高和平均胸径外，同时还调查并记录了各样地马尾松林的龄组、海拔、坡度、坡向、坡位及林分密度等。由于所调查的样地林分密度为156 0～163 0株·hm-2，较为接近，对研究区样地马尾松生长影响不大，故未考虑林分密度对马尾松的影响。各县（市）样本的树高和胸径数据见表1。

表1 样木基本情况Tab.1 Basic information of sam ple wood

2.2 研究方法

2.2.1 立地因子等级划分

参照《中国森林立地》划分标准，对调查的海拔、坡度、坡位、坡向等4个立地因子进行分级［12］。其中，为了区分不同海拔梯度的影响，将海拔每200 m划分为一级，具体划分标准见表2。

表2 立地因子等级划分Tab.2 Classification of site factors

2.2.2 显著性影响因子选取

基于R 4.2.3软件，采用方差分析、多重比较Scheffe法［13］并采用箱线图将结果可视化，对湘西8个不同区域、4个不同龄组（这里将成熟林与过熟林归为一组）、不同立地因子（包括不同海拔、坡度、坡向以及坡位）间的树高是否存在显著差异进行分析，从而筛选出对湘西土家族苗族自治州马尾松树高生长影响显著的因子。

2.2.3 基础模型的筛选

选取6组基本非线性模型（3个2参数模型和3个3参数模型）作为基础模型（表3），比较它们的模型精度，选取最优基础模型进而构建马尾松树高-胸径混合效应模型。

表3 候选基础模型Tab.3 Candidate basic models

2.2.4 混合效应模型构建

大量研究表明树高-胸径模型的构建过程中，树高除了与胸径呈明显数量关系外，其他变量也会影响树高曲线的变化，包括立地条件、林分因子、竞争以及经营措施等［20-22］。本研究在最优基础模型的基础上，考虑到区域、龄组以及4个不同立地因子对树高曲线的影响，选择其中的显著性影响因子，拟构建包含这些显著性影响因子及其组合随机效应的马尾松树高-胸径混合效应模型，进而从中择出最优模型。非线性混合效应模型（nonlinear mixed-effectmodels，NLMEMs）是依据回归函数依赖于效应参数非线性关系而建立的数学模型，其中，效应参数包括固定效应参数和随机效应参数，这里假设区域因子显著，以其作为随机效应为例，其一般形式如下［23］：

式中：hi与Di分别为第i个区域的林分平均高和林分平均胸径，εi为误差向量，β、μi分别为固定效应参数和随机效应参数。

混合效应模型在参数效应和随机效应的方差协方差结构确定后，有两个问题必须要考虑：一是模型的异方差，二是模型的自相关性［24］。由于本研究的数据不是重复观察数据，所以不需要考虑自相关性。

2.2.5 模型评价与检验

使用R 4.2.3软件的nls函数、nlme包的nlme函数分别对上述基础模型以及混合效应模型进行拟合，求解模型参数、计算模型精度评价与检验指标。以赤池信息量准则 （Akaike information criterion，AIC）及贝叶斯信息准则 （Bayesian information criterion，BIC）选择基础模型 （即AIC、BIC值越小，模型拟合效果越好），同时对模型进行F检验，判断模型回归效果是否显著。采用留一交叉验证法［25-26］对模型进行检验，在此过程中，假设样本量为n，将单个观测值用于验证集，其余n-1个观测值作为训练集；然后，对排除的观测值进行预测，并在n-1个观测上重复n次此过程，产生n个测试误差估计；基于n个测试误差估计值计算确定系数 （R2）、均方根误差（root mean square error，RMSE）、总相对误差（total relative error，TRE）。R2越接近于1，RMSE值、TRE的绝对值越小，模型精度越高。根据3个指标计算结果比较基础模型与树高-胸径混合效应模型的拟合效果。各指标计算公式如下：

式（2）～（6）中：CAI为赤池信息量准则值，CBI为贝叶斯信息准则值，R2为确定系数，ERMS为均方根误差，ETR为总相对误差，n为样本数，l表示模型极大似然函数值，p为模型中参数的个数，hi为第i样本树高实测值，是第i样本树高预估值，为实测树高的平均值。

3 结果与分析

3.1 影响因子筛选及树高差异特征分析

由方差分析可知：区域、龄组以及4个立地因子（海拔、坡度、坡向、坡位）中，区域、龄组、坡向为研究区内马尾松树高的显著性影响因子（P＜0.05）（表4）。通过Scheffe法多重比较以及箱线图可视化（图1）可得：研究区8个不同县（市）内的马尾松树高生长差异明显，其中古丈县的马尾松整体长势最好，而花垣县、龙山县马尾松的树高总体偏低；从龄组来看，马尾松树高随幼龄林、中龄林、近熟林以及成熟林、过熟林趋势增加，其中马尾松成熟林、过熟林明显高于幼龄林、中龄林；不同坡向间马尾松树高生长差异显著，研究区半阳坡马尾松树高整体高于其他三个坡向的；研究区内不同海拔、坡度、坡位马尾松树高整体差异均不显著。

图1 不同区域、龄组以及立地条件马尾松林分平均高Fig.1 Stand mean height of Pinusmassoniana in different regions，age groups and site conditions

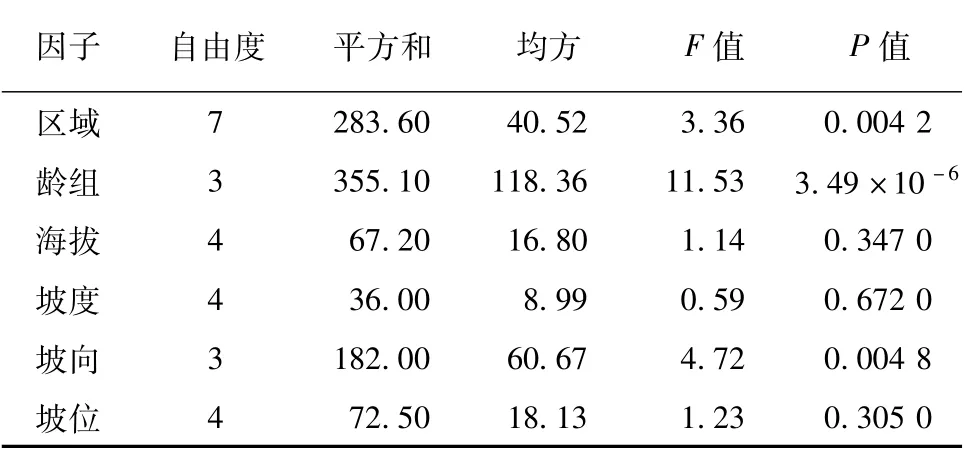
表4 影响因子的显著性检验Tab.4 Significance test of influence factors

3.2 基础模型的拟合与筛选

使用R语言的nls函数对6个树高-胸径基础模型进行拟合，得到模型拟合参数，并使用R2、AIC、BIC对基础模型进行筛选，具体结果如表5所示。由表5可知，6个基础模型的R2相差不大，为0.493 7～0.510 6，其中3参数模型M4的R2最大，但其3个参数a、b、c中仅参数a显著（具有统计学意义）。而AIC、BIC值最小的模型为2参数模型 M2 （Schumacher）， R2＝0.509 7、AIC＝347.636 4、BIC＝354.424 4，同时其参数a、b均极显著，具有统计学意义。综合可得，选择M2为最优基础模型。

3.3 混合效应模型构建

使用R语言中nlme包nlme函数拟合树高-胸径混合效应模型。根据3.1的显著性因子筛选结果，本研究考虑的随机效应因子为区域（AR）、龄组（AG）、坡向（AP）。在最优基础模型M2中加入这些随机变量，拟合结果如表6所示。

表6 混合效应模型参数估计及模型精度评价Tab.6 Parameter estimation and model accuracy evaluation ofm ixed-effectsmodels

根据R2、RMSE、TRE可以看出，混合效应模型的拟合效果均优于最优基础模型。只含一个随机效应因子时，M2.3拟合效果最好；当包含两个随机效应因子时，M2.12拟合效果最好；当包含三个随机效应因子时，M2.21拟合效果最好。同时，可以看出M2.21的拟合效果优于其他任意一个模型，其模型精度最高，R2＝0.845 3，与最优基础模型M2相比精度提升了65.84%；RMSE、TRE分别为1.730 0、 -0.060 7，RMSE 比 M2 的降低了39.01%，TRE绝对值比M2的降低了73.52%。

一般地，可以通过比较拟合模型的残差分布图很好地判断误差的异方差性。本研究绘制2个不同模型的残差图用以检验拟合模型是否存在异方差情况（图2）。从图2可以看出，最优基础模型M2、最优混合效应模型M2.21的残差均表现为随机分布的趋势，不存在明显异方差。同时可以发现，最优混合效应模型M2.21残差分布更加收敛，拟合精度高于最优基础模型M2。

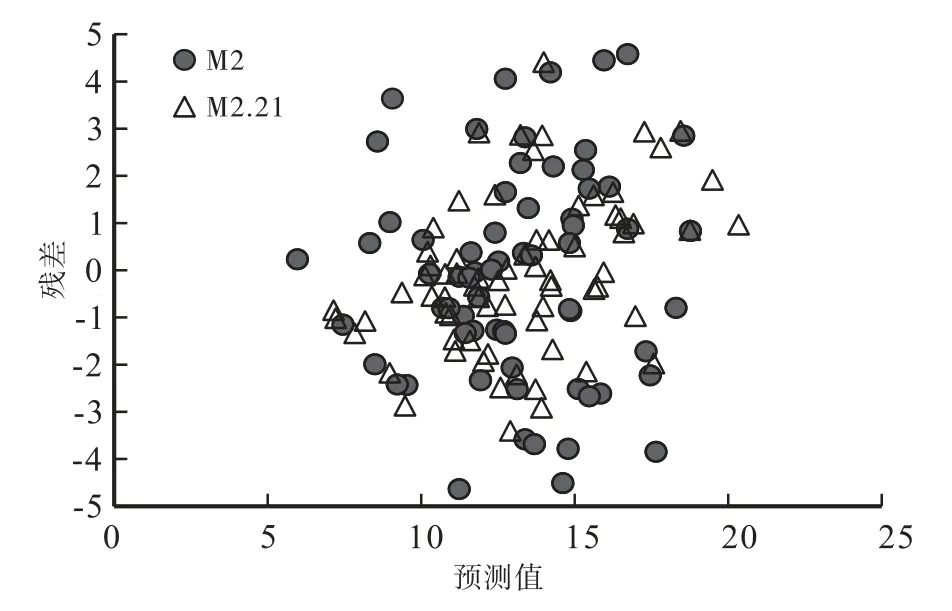
图2 最优基础模型M 2与最优混合效应模型M 2.21的残差图Fig.2 Residual plot of optimal basic model M 2 and optimalm ixed-effectsmodel M 2.21

4 结论与讨论

4.1 结论

本研究以湘西土家族苗族自治州8个县（市）采集的马尾松样本数据为基础，首先利用方差分析筛选出研究区马尾松树高生长显著性影响因子，同时通过多重比较Scheffe法以及箱线图可视化方法对不同区域、龄组以及立地条件的树高差异特征分析；然后采用最小二乘法拟合6个候选基础模型，选择最优基础模型；最后构建含显著性影响因子及其组合的混合效应模型，并比较最优基础模型与混合效应模型以及混合效应模型之间的拟合精度、拟合误差、模型复杂程度，筛选出适用于湘西土家族苗族自治州的最优树高-胸径模型。主要结论为：

（1）区域、龄组、坡向为研究区内马尾松树高的显著性影响因子。研究区8个不同县（市）内的马尾松树高生长差异明显，其中古丈县的马尾松整体长势最好，而花垣县和龙山县的马尾松树高总体偏低；从龄组来看，马尾松树高随幼龄林、中龄林、近熟林以及成熟林、过熟林趋势增加，其中马尾松成熟林、过熟林明显高于幼龄林、中龄林；不同坡向间马尾松树高生长差异显著，研究区半阳坡马尾松树高整体高于其他三个坡向的；研究区内不同海拔、坡度、坡位马尾松树高生长整体差异并不显著。

（2）6组候选基础模型中，M2（Schumacher）模型最优，其AIC、BIC值最小，分别为347.636 4、354.424 4，R2＝0.509 7，同时其参数a、b均极显著，具有统计学意义。

（3）在21个混合效应模型中，最优混合效应模型为M2.21，即区域、龄组、坡向作为随机效应同时作用在最优基础模型M2的参数a、b时的混合效应模型，其模型精度最高，R2＝0.845 3，与最优基础模型M2相比精度提升了65.84%；RMSE、TRE分别为1.730 0、-0.060 7，与M2相比，RMSE降低了39.01%，TRE的绝对值降低了73.52%。

4.2 讨论

马尾松林是湘西土家族苗族自治州主要用材林之一，其在生产经济用材、涵养水源、维持碳平衡等方面有着关键作用。建立准确有效的马尾松林树高-胸径模型对指导湘西土家族苗族自治州林业生产和实践具有重要的现实意义。以往的研究表明，不同地区、不同林分类型以及不同生境条件下的林分生长规律不一。Zeide等［27］研究发现，林分密度是影响树木的胸径-树高关系的主要因素。Meng等［28］研究表明，包含环境变量的树高-胸径模型能够更好地预测不同区域内的加州扭叶松（Pinus contorta var.latifolia）树高。本研究显示，区域、龄组以及坡向是影响湘西土家族苗族自治州马尾松林树高的主导因子，不同区域的综合立地条件、微气候、土壤理化性质不一，从而导致马尾松树高生长具有差异；不同的龄组本身反映了马尾松林生长的时间差；而不同坡向则影响了马尾松林生长的光照时间与强度，从而使其生长产生差异。实际上，许多研究表明林分密度是影响树木生长的关键因子之一，陈浩等［7］构建了贵州省东北部地区马尾松人工林树高-胸径非线性混合效应模型，发现将密度、优势木平均高、胸高断面积以不同个数及组合形式加入基础模型，同时考虑样地水平随机效应的混合效应模型预测精度高、适用性强。本研究各样地林分密度相近，尚未考虑林分密度对研究区内马尾松生长的影响，在后续的研究中，可补充调查不同林分密度的马尾松人工林样地，探究林分密度对湘西土家族苗族自治州马尾松人工林生长的作用机制。

同时，不同基础模型对不同地区、不同林分类型林分以及不同生境林分的适用性也不一样。Xu等［6］在构建中国东南地区杉木单木树高-胸径模型时发现，5个代表性基础模型中，Korf模型最优；而王君杰等［29］研究发现，12个基础模型中，Richards方程更适用于大兴安岭的落叶松（Larix gmelinii）树高-胸径模型的构建。本研究选取了6组非线性树高-胸径基础模型，其中Schumacher模型（M2）最适用于湘西土家族苗族自治州马尾松林树高-胸径模型的拟合。

混合效应模型具有很好的兼容性，能够将复杂的立地、林分以及干扰等因子在模型中表达出来，通过这种方法构建的模型往往优于传统最小二乘法构建的回归模型，符利勇等［5］、段光爽等［30］以及Bronisz等［31］证明了这一点。考虑到湘西土家族苗族自治州地处云贵高原东侧的武陵山区，地形地貌复杂多样，以及调查的各龄组、坡向马尾松林树高差异显著，本研究构建了包含区域、龄组、坡向随机效应的马尾松树高-胸径混合效应模型，结果显示混合效应模型拟合效果均优于基础模型。另外，本研究尚未采用分位数回归、贝叶斯分层模型以及机器学习等方法来构建湘西土家族苗族自治州马尾松林树高-胸径模型，未来可比较这些方法拟合模型的优劣性，进一步为湘西土家族苗族自治州马尾松林林业生产实践提供理论基础。