基于大数据分析的工业控制系统故障检测方法

胡 迪

(成都锦城学院 四川 成都 610000)

0 引言

互联网已经在物联网、无线通信、移动设备、电子商务和智能制造等领域收集了海量数据,这种数据的增长速度呈指数级[1]。这样的爆炸式增长使得这些领域对于大数据的概念和力量产生了认识。大数据不仅有望为这些领域提供新的思路,以处理和发现有价值的信息,而且还有可能促进这些领域对其他领域的影响,例如工业控制系统的状态监测和故障诊断领域[2]。在现代工业中,机器变得越来越自动化、精确和高效,使得机器的健康状况监测变得更加困难。为了全面检查机器的健康状况,需要使用状态监测系统收集机器的实时数据,并通过多个位移传感器获取大量的机械数据,由于数据的收集速度普遍快于诊断分析数据的速度,因此如何从机械大数据中有效地提取特征并准确识别相应的健康状况已成为当前亟须解决的研究问题。智能故障诊断能够快速有效地处理大量采集到的机械振动信号并提供准确的故障诊断结果,因此它可能成为处理工业控制系统中大数据的一种工具[3]。

传统的智能故障诊断框架包括3个主要步骤:信号采集、特征提取和选择以及故障分类[4]。在信号采集步骤中,振动信号被广泛采用,因为它们提供了机械故障的内在信息。在第2步中,特征提取旨在使用信号处理技术从采集的信号中提取代表性特征,如时域统计分析、傅里叶谱分析和小波变换。然而,传统的人工智能技术无法直接从原始数据中提取和组织判别信息。因此,智能诊断方法中的大量实际工作都被用于特征提取算法的设计,以从信号中获取具有代表性的特征。但是特征通常是根据特定的诊断问题提取和选择的,可能不适用于其他问题,在处理新的诊断任务时可能需要重新设计特征提取算法。

为了克服传统智能故障诊断方法中的弱点,需要采用先进的人工智能技术来自适应地学习特征,而非手动提取和选择特征。这将使智能故障诊断方法减少对先验知识或人工的依赖,从而可以更快地应用于新的场景,实现真正的人工智能故障诊断。无监督特征学习是一种有潜力克服传统方法弱点的技术,它的基本思想是训练人工智能技术去学习一个非线性函数,将原始数据从原始空间转换到特征空间[5]。因此,无监督特征学习是一组算法,研究如何利用未标记的原始数据很好地训练人工智能技术,从而自动学习分类所需的判别特征。受无监督特征学习思想的启发,提出了一种新的智能故障诊断框架。该框架直接从原始机械振动信号中学习特征,并使用分类器对整个工业控制系统故障进行分类。该框架的优势在于,特征是使用通用学习程序从原始信号中自动学习得到,而不是由诊断人员手动提取。

1 故障诊断方法的总体框架

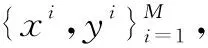
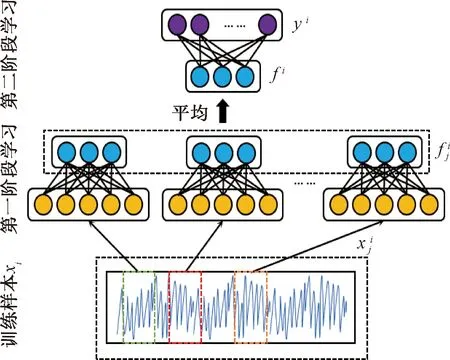
图1 基于大数据分析的工业控制系统的故障检测框架

稀疏滤波是一种无监督学习算法,它可以自适应地学习输入数据的特征。与传统的信号滤波算法不同,稀疏滤波不仅可以去除噪声,还可以提取输入数据中的有用信息,从而获得更加紧凑、更具代表性的特征。其基本思想是,将输入数据表示为一个稀疏的线性组合形式,其中每个组件(即滤波器)具有高度的稀疏性,即大部分权重都是零。这些稀疏的滤波器是自适应地学习的,可以从输入数据中提取出最有代表性的特征。稀疏滤波的实现使用一种称为L1正则化的方法来促进稀疏性[10-12]。L1正则化是指在目标函数中添加一个L1范数惩罚项,以鼓励大部分权重为零。通过这种方式,稀疏滤波可以自适应地学习滤波器,同时保持高度的稀疏性。

Softmax回归是一种用于多分类问题的机器学习算法,主要将输入数据分为2个以上的互斥类别,并给出每个类别的概率预测。它是逻辑回归的一种推广,可以将逻辑回归扩展到处理具有多个类别的问题,其目标是学习一个可以将输入向量映射到每个可能的类别的概率分布的模型。Softmax回归首先对每个可能的类别计算一个得分,然后将这些得分作为输入,通过一个Softmax函数,将它们转换为概率分布,最终确定输入向量所属的类别,并且将每个得分除以所有得分之和,从而确保它们都在0和1之间,并且它们的总和为1。

2 第1学习阶段

在第1阶段,首先训练稀疏滤波并获得其权重矩阵W,然后使用经过训练的稀疏过滤来捕获每个样本的局部特征,最后对这些局部特征进行平均,从而得到每个样本的学习特征。

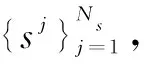
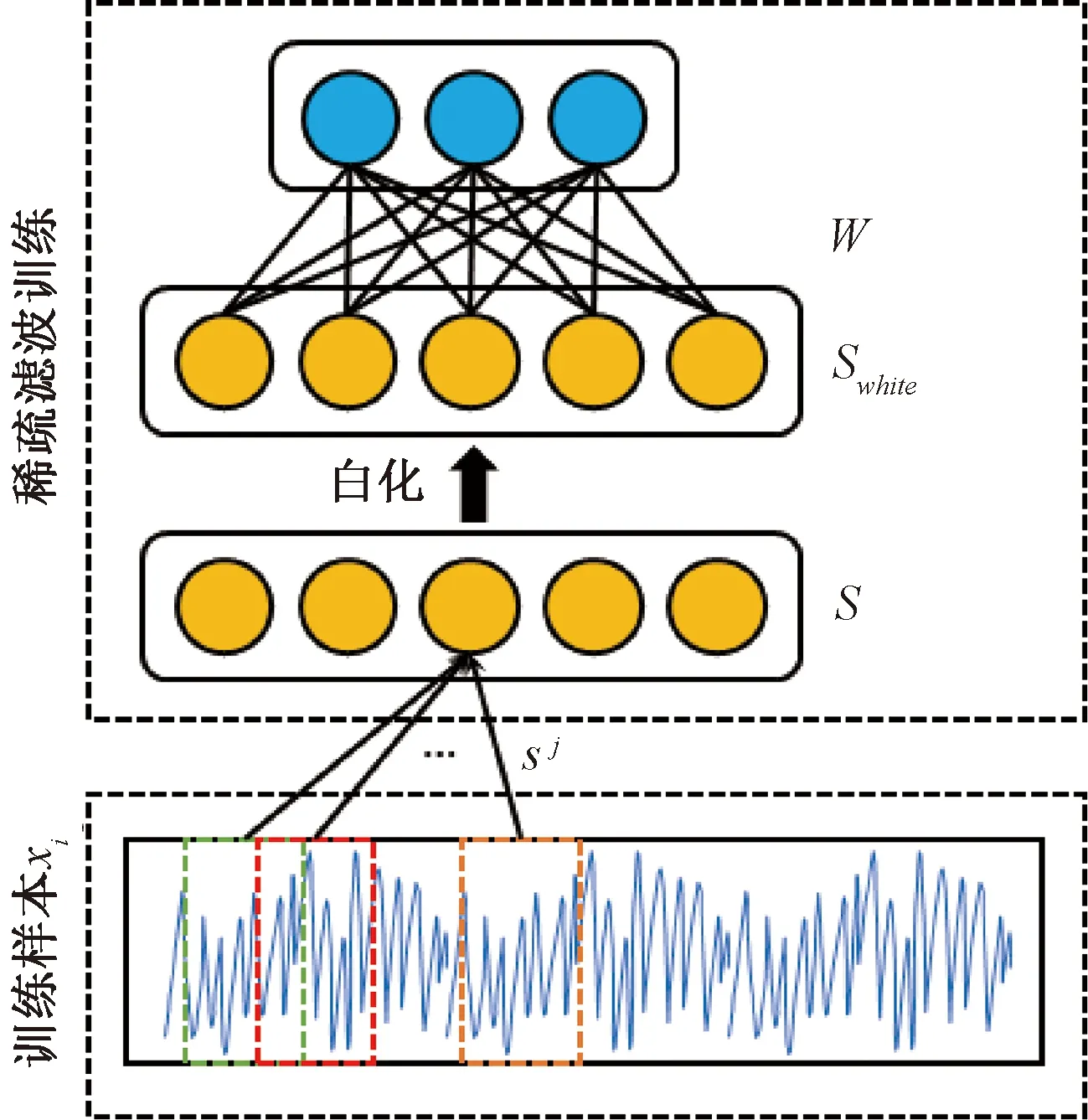
图2 稀疏过滤训练过程示意图

fov(S)=EDET

(1)

其中,E是方差矩阵cov(S)的特征向量的正交矩阵,D是其特征向量的对角矩阵。因此,可以获得白化的训练片段集SWhite:

(2)

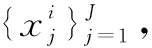
(3)

本方法使用平均的方式而不是直接合并的方式来得到特征:

(4)

平均的方式有助于增强不同片段彼此共享的判别特征并抑制由噪声引起的随机特征。

3 第2学习阶段

(5)

其中,θ=[θ1,θ2,…,θK]T为Softmax回归模型的参数,所有类别标签上的概率总和为l。经过训练后,hθ(xi)中最大的概率值对应了特征fi最终属于的故障状况标签。

在2个学习阶段之后,使用测试样本来验证所提出的方法。对于每个测试样本,首先将其交替划分为多个片段,然后使用训练好的稀疏过滤模型从片段中获取局部特征。接下来,通过对这些局部特征进行平均来获得每个测试样本的学习特征。最后,测试样本的故障状况由经过训练的 Softmax 回归模型使用学习到的特征来决定。

4 实验与分析

为了验证工业控制系统故障检测方法,采用振动信号数据集来对工业控制系统的故障做模拟,对该框架进行训练并测试。MFPT是一个常用的用于故障诊断和状态监测研究的数据集。该数据集由美国宾夕法尼亚州贝克利大学的Machinery Failure Prevention Technology(MFPT)中心收集和发布。MFPT数据集的收集过程涵盖了多个工业设备,包括齿轮箱、轴承、齿轮和轴等。为了模拟真实工业环境中的故障情况,这些设备在不同的工况下运行,并引入了多种常见的故障类型,如齿面磨损、轴承松动和齿轮缺陷等。采集数据集时,每个设备都安装了用于测量振动信号的传感器,这些传感器以恒定的采样频率记录振动数据。数据集中的振动信号以时间域和频域2种形式提供。时间域数据是指原始的时域振动信号,频域数据是通过对时间域信号进行傅里叶变换得到的频谱特征。MFPT数据集还提供了故障标签信息,用于指示每个设备在每个时间点是否存在故障。这些标签信息对于训练和评估机械故障诊断算法非常重要,可以帮助研究人员建立准确的故障预测模型。

用该数据集进行训练和测试时:

(1)数据集准备:获取MFPT轴承数据集并将其分为训练集和测试集(训练集与测试集比例为8∶2),其中训练集用于训练模型,而测试集用于评估模型的性能。

(2)数据预处理:对原始振动信号进行预处理,包括去除噪声、归一化和滤波等。

(3)特征提取:使用稀疏滤波从预处理的振动信号中提取局部判别特征,将这些局部特征平均为信号的学习特征。

(4)模型训练:使用训练集和学习特征来训练 Softmax 回归模型。训练过程中,通过反向传播算法来更新模型参数。

(5)模型评估:使用测试集来评估训练好的模型的性能。

在实验中,使用准确率、精确率、召回率和F1值4个指标进行模型评估,如表1所示。可以看出,实验中大部分测试样本都被正确分类,准确率达到了0.95,表明模型对于故障和非故障样本的分类效果较好,能够较准确地对样本进行分类。精确率和召回率都比较接近,分别为0.94和0.96,表明系统在正确判别故障和非故障样本方面表现都优秀。F1值是精确率和召回率的调和平均值,综合考虑了模型的精确率和召回率。F1值为0.95,说明该方法具有良好的综合故障诊断性能,能够较好地平衡精确率和召回率之间的关系。

表1 MFPT数据集对模型训练和评估结果

5 结语

在工业控制系统的大数据处理中,特征提取是智能故障诊断中的一个重要步骤。为了减少该过程对先验知识和专业诊断知识的依赖,提出了一种基于无监督特征学习思想的两阶段学习方法。该方法的第1阶段使用稀疏滤波器以无监督方式自适应地学习机械振动信号的代表性特征。在第2阶段中,使用了一个双层网络的Softmax回归器来自动分类机械的健康状况。由于所提出的方法使用神经网络学习特征,因此不依赖先验知识和人工干预,可能更适用于处理海量信号的状态监测和故障诊断领域。未来,拟将训练好的模型部署到实际工业控制系统中进行故障诊断,该过程可能需要不断优化和改进模型以提高其性能和稳定性。