基于GRU网络的格兰杰因果网络重构

杨官学，王家栋

（江苏大学 电气信息工程学院，江苏 镇江 212013）

0 引言

现实生活中，许多复杂系统均可在网络角度被抽象表达，其中网络节点代表系统变量，连边代表各变量间的相互作用关系。基于关联的属性和特征，网络可被划分为不同种类，例如根据边是否有权重或方向，网络可被分为有权网络和无权网络、有向网络和无向网络。典型的网络包含电力网络、脑网络、生物网络、交通网、人际网［1-2］等。然而，实际的网络结构往往是未知或难以直接观察。在当今大数据时代，复杂网络涵盖的信息量越来越多，如何基于隐藏在节点背后的数据挖掘节点间的作用关系，就显得至关重要，这也使得复杂网络重构成为当前研究的热点方向之一［3-4］。复杂网络重构不仅能使人们更好地了解系统的动力学行为和演化机制，也是后续网络结构研究和分析的基础。例如，针对脑神经网络研究大脑神经元间如何相互激活［5］；针对基因调控网络从基因表达水平的时间序列推断基因调控网络［6］等。

当下，复杂网络重构算法包括相关系数［7-8］、互信息［9-11］、布尔网络［12-13］、贝叶斯网络［14］、格兰杰因果［15］、压缩感知［16］等。尤其在有向网络的推断方面，格兰杰因果（Granger Causality，GC）及其拓展形式得到了广泛应用。传统格兰杰因果是一种基于线性矢量自回归模型的判定方法，能判断两个时间序列变量间的因果关系，但当网络中存在两个以上变量时可能会导致虚假连边。为此，提出条件格兰杰因果来解决多个变量间的间接影响［17］。

此外，针对样本量不足的问题，在考虑实际网络稀疏性的前提下，很多学者将稀疏特征引入格兰杰因果中，提出LASSO 格兰杰因果［18］、组稀疏格兰杰因果［19］、基于贪婪算法的格兰杰因果［20］等方法，这些方法虽然结构形式简单、运算方便，但无法匹配非线性因果关系的处理情形。因此，很多学者将核函数引入传统格兰杰因果中提出核格兰杰因果方法［21-22］，但本质上还只是针对某种特定的非线性情形，适用范围存在一定限制。

考虑到神经网络在非线性建模方面能非常擅长地处理输入和输出间复杂的非线性关系。在因果预测方面结合格兰杰因果模型、多层感知机（Multi-Layer Perceptron，MLP）、循环神经网络（Recurrent Neural Network，RNN）及长短期记忆元（Long Short-Term Memory，LSTM）已得到了应用。Chivukula 等［23］使用RNN 分析雅虎财经获取的真实股市数据，结果表明因果特征显著改善了现有的深度学习回归模型。Pathod 等［24］使用RNN 和LSTM 处理多元脑连接性检测问题提出了RNN-GC 模型，能对非线性和变长时延信息传输进行建模，并在方向性脑连接性估计方面十分有效。Tank 等［25］使用MLP 和LSTM 在时序数据上进行建模，并融合LASSO 提取节点间的因果关系，两种方法均能自动探索最大滞后阶数，且在复杂非线性DREAM3 数据上取得了较好的结果。

然而，MLP、RNN 存在收敛慢、容易过拟合、可解释性差、计算复杂度高等缺点。其中，RNN 的循环结构使其可能无法很好地处理长期依赖关系，易出现梯度消失或梯度爆炸现象；LSTM 在RNN 上进行改进，不易出现梯度问题，但在处理噪声较大的数据时性能较差。相较于LSTM 网络，GRU 网络结构仅有更新门和重置门，更容易训练。因此，考虑到变量间影响关系的非线性和因果性，本文提出一种基于门控循环单元（Gated Recurrent Unit，GRU）网络的格兰杰因果网络重构方法（GRUGC）。首先围绕每个目标节点，构建基于GRU 网络的格兰杰因果模型；然后对网络输入权重进行组稀疏惩罚约束；最后基于Adam 的梯度下降网络训练法，获取节点之间的格兰杰因果关系。

在仿真验证方面，首先基于模型生成的数据集进行相关仿真研究，例如线性矢量自回归、非线性矢量自回归、非均匀嵌入时滞矢量自回归、Lorenz-96 模型。然后，采用经典的DREAM3 竞赛数据集（Ecoli 数据集和Yeast 数据集）分析模型性能。

1 格兰杰因果模型

在格兰杰因果分析中，传统分析方法通常采用线性矢量自回归模型（Vector-Autoregression，VAR），设模型的最大时滞阶数为P。

式中：Xt为模型中所有变量在t时刻的样本矩阵。可表示为：

式中：N为模型变量个数；M为样本数目；xi，t∈R1×M为第i个变量在t时刻的样本向量为 第i个 变量 在t时刻的第m个样本值；i=1，2，…，N；m=1，2，…，M；p为模型阶数为t-p时刻Xt-p对应的系数矩阵。可表示为：

式中：p=1，2，…，P表示在t-p时 刻第i个 变量和第j个变量间的影响关系；Xt-p∈RN×M为模型变量在t-p时刻的样本矩阵，形式如Xt；et∈RN×M为服从标准正态分布的噪声。

在VAR 中，当且仅当对所有阶数p有=0，即可获得变量j不是影响变量i的格兰杰原因；反之，变量j是影响变量i的格兰杰原因，即存在一条从变量i指向变量j的有向边。在高维情况下考虑到稀疏性，格兰杰因果模型可被认为是一个带有组稀疏正则化的回归问题。

式中：‖•‖2为ℓ2正则化，目的是防止模型发生过拟合现象；λ为惩罚系数。

2 神经网络格兰杰因果模型

为了解决传统格兰杰因果模型无法有效处理非线性关系的问题，提出了一种基于神经网络的格兰杰因果模型。首先构建一个通用的非线性矢量自回归模型，假设该模型中变量的个数为N，最大时滞阶数为P，则模型t时刻的输出yt的通用表达式如式（5）所示。

式中：f(•)为输入输出间的非线性映射函数关系为在t之前时刻模型各输入时滞分量的集合，即=1 ≤p≤P；et为服从标准正态分布的高斯白噪声。

目前，通常使用神经网络对非线性函数f(•)进行预测，常见方法包括MLP、RNN、LSTM 等。由于神经网络为黑盒模型，且模型中各输入共享隐藏层，难以直接进行因果推断的分析研究。因此，在式（5）中并未直接采用常规的多输入多输出映射来获取时序变量间的关系。

为了进一步详细阐述模型的原理，将整个网络重构任务分解为每个目标节点的邻居节点选择问题。针对每个目标节点i分别使用单独的模型fi(•)，以清晰地提取与邻居节点间的格兰杰因果关系。节点i在t时刻的表达值xi，t由式（6）所示。

式中：fi(•)采用的是GRU 网络。

同理，当且仅当所有阶数p(1 ≤p≤P)在有关xi，t的预测时不依赖节点变量j的时滞分量，即在预测模型中加入{xj，t-1，xj，t-2，…，xj，t-P}后并不能提升对xi，t的预测精度，则认为节点j不是影响节点i的原因；反之，节点j是影响节点i的原因，即存在j→i。

2.1 基于GRU的循环神经网络

RNN 属于一种具有短期记忆能力的神经网络，尤其适用于处理和预测时间序列数据，作为一种常用的深度学习环路网络结构模型，RNN 由一个或多个循环层组成，每个循环层包含多个神经元，不仅能接收其他神经元信息，还能接收自身信息。理论上，RNN 可逼近任意的复杂非线性动力系统。在RNN 网络参数训练过程中，由于链式法则，随着错误信息的反向传播，当输入序列时间步长较长时，梯度值可能会趋近于0（梯度消失）或非常大（梯度爆炸）。这两种情况均会导致训练效果不佳。为了解决RNN 的长程依赖问题，在本文提出神经网络格兰杰因果模型的框架中，采用了基于门控循环单元（Gated Recurrent Unit，GRU）的循环神经网络结构模型，如图1所示。

Fig.1 Gated loop unit structure of GRU networks图1 GRU网络的门控循环单元结构

GRU 内部结构主要由两个门构成，分别为重置门rt∈[0，1]D（reset gate）和更新门zt∈[0，1]D（update gate），通过调节这两个门的激活值来控制信息流动，解决梯度消失问题，以能更好地捕捉序列中的长期依赖关系。GRU 单元的内部计算式如式（7）—式（10）所示：

式中：xt∈RN×1为t时刻网络输入；ht∈RD×1为t时刻隐含层的状态；W*∈RD×N、U*∈RD×D、b*∈RD×1为待学习的神经网络参数；*属于集合{r，z，h}中的元素；⊙为Hadamard Product，表示矩阵对应位置元素的乘积。

重置门rt和更新门zt状态的迭代更新来源于上一时刻的隐藏层ht-1和当前时刻的输入节点xt，待获得ht-1、xt后分别通过式（7）、式（8）计算重置门rt和更新门zt的值。式（9）首先使用rt⊙ht-1更新数据得到；然后与各自权重相乘后将Whxt与相加完成特征融合；最后使用tanh函数将特征值映射到［-1，1］，得到中具有上一时刻的隐含层状态ht-1和当前输入状态xt的信息。

式（10）为GRU 最重要的一步，在这个阶段遗忘和记忆同时进行，既忘记ht-1中部分信息，又记住中节点输入的部分信息。GRU 网络直接用一个门来控制输入和遗忘间的平衡关系，当zt越接近1 表示记住的数据越多，反之遗忘的越多。

针对时间序列输入xt，将xt在不同时刻输入到循环神经网络中得到相应的隐含层状态ht，循环神经网络的输出yt最终由ht的加权线性求和表示，如式（11）所示。

式中：Wo∈RD×1为输出层权重；Wo为待学习的网络参数。

2.2 基于GRU网络的格兰杰因果

在因果网络重构问题中，根据式（6）、式（11）针对每个目标节点i构建子任务优化模型，分别得出相应的邻居节点。具体表达形式如下：

针对输入节点变量xt，将输入层至隐含层的权重矩阵Wr、Wz、Wh进行堆叠拼接以便于后续优化，由M=表示总输入权重矩阵。为了捕捉驱动节点j对目标节点i的因果影响，当且仅当总输入权重矩阵M的第j列均为0，即M：，j=0得出驱动节点j对目标节点i不存在因果关系；反之驱动节点j是影响目标节点i的原因，即存在j→i的连边。此外，合理加入正则项能提升神经网络模型的泛化能力，ℓ2正则化项的惩罚因子λ同时也是控制网络结构稀疏性的参数［26］。

2.3 基于Adam的梯度下降法

当下，最流行的神经网络学习优化方法大都始于随机梯度下降法（Stochastic Gradient Descent，SGD）［27］，但SGD每次只用一个样本更新梯度，使得SGD 并非每次迭代均向最优方向更新参数，容易造成准确度下降且无法线性收敛的情况。同时，由于只用一个样本更新梯度并不能代表全部样本的趋势，因此易陷入局部最小值。

为此，本文采用基于以往梯度信息和动量的Adam［28］优化方法。该方法是RMSProp 和动量法的结合，主要纠正两项偏差和平均梯度滑动的方法，具体计算过程如下：

步骤1：初始化学习率lr、平滑常数β1、β2（分别用于平滑mt、vt），可学习参数θ0=0、m0=0、v0=0、t=0。

步骤2：当未停止训练时，更新训练次数t=t+1，计算梯度gt（所有的可学习参数都有各自梯度，因此gt指全部梯度的集合）。

本文神经网络模型的训练方法采用了以Adam 为基础的优化方法。为了研究正则项的影响，训练采用了无正则项的AdamU 和有正则项的Adam。

3 仿真实验

为了验证本文所提基于GRU 网络的格兰杰因果网络重构算法的有效性，分别基于线性VAR、非线性VAR、Lorenz-96、非均匀嵌入时滞VAR 模型及DREAM 竞赛数据集进行仿真实验研究。网络重构性能的具体量化性能指标采用ROC 曲线下的面积（Area Under Receiver-Operating-Characteristic Curve，AUROC）和PR 曲线下的面积（Area Under Precision-Recall Curve，AUPR）。

3.1 线性VAR

首先基于N=10 的VAR 网络模型，利用式（1）随机生成的稀疏转移矩阵生成仿真时间步长T=1 000 的时间序列数据。噪声服从高斯分布N(0，σ2)，σ=0.1，基准因果网络如图2 所示。由此可见，若节点与节点间存在GC 关系，则对应区间的数值大小为1；若不存在GC 关系，则对应区间的数值大小为0。例如，图2 中（1，1）位置和（1，9）位置的数值大小均为1，分别表示存在一条由节点1 指向节点1的GC 边和存在一条由节点1指向节点9的GC 边。

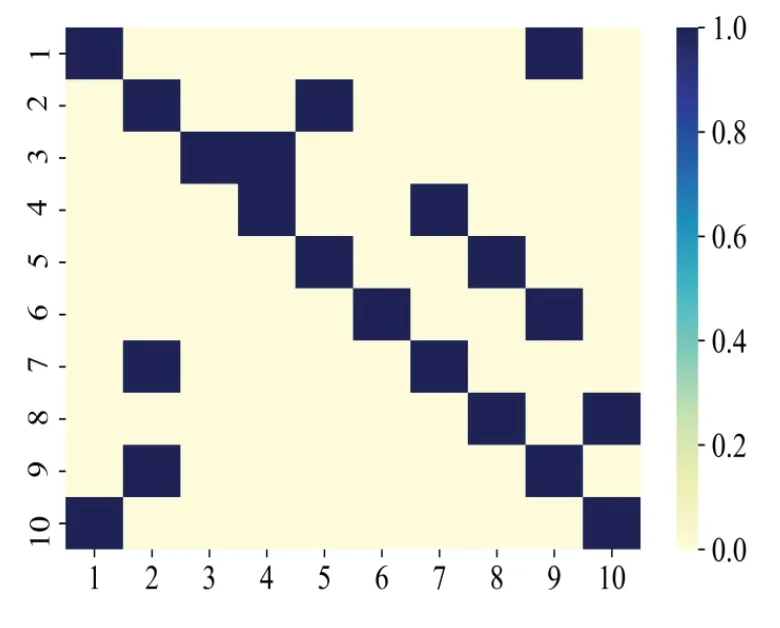
Fig.2 Benchmark network of VAR model图2 VAR模型基准网络

具体参数设置如下：针对每一个目标节点i，创建自我依赖关系（自环），并在其他N-1 个节点中随机选择一个驱动节点构建因果关系，即在j→i的情况下设置0.1，p=1，2，3，同时令其他=0。GRU 网络模型的隐藏层单元数D设定为100，分别比较Adam、AdamU 两种训练优化方法，最大滞后阶数P=5，正则系数λ=0.002，学习率lr=0.05，训练步长为20 000，AdamU 无需设置正则系数λ。

VAR 模型的两种训练方法仿真结果如图3 所示，图中区域数值大小表示经过GRUGC 推理后存在GC 边的概率值。与图2 的基准网络比较可见，考虑正则化的Adam 相较于考虑正则化的AdamU 效果更好。

Fig.3 Results of two training methods for VAR model图3 VAR模型的两种训练方法结果

为了量化每种训练方法的性能，计算图3 不同方法的AUROC 和AUPR，具体数值如表1 所示。由此可知，Adam的AUROC 和AUPR 均达到1，实现了完美的因果网络重构，而AdamU 的AUROC、AUPR 仅为0.225、0.125。

Table 1 Performance comparison of two training methods for VAR model表1 VAR模型的两种训练方法性能比较

3.2 Lorenz-96

设置网络节点个数N=10，F=10，添加服从高斯分布的噪声N(0，0.012)，获得序列长度T=1 000 的多变量时间序列矩阵。Lorenz-96 模型的微分方程表达式（14）所示，可得N=10的Lorenz-96模型的基准网络如图4所示。

Fig.4 Benchmark network of Lorenz-96 model图4 Lorenz-96模型的基准网络

式中：i=1，2，…，N；F为惩罚力度，值越大表示时间序列的非线性越强。

设置GRU 网络模型的隐藏层单元数D=100，比较Adam 和AdamU 两种训练优化方法，最大滞后阶数P=10，正则系数λ=0.2，学习率lr=0.001，训练步长为10 000。Lorenz-96 模型的两种训练方法结果及相关性能指标如图5、表2 所示。由此可见，经AdamU 训练获取的网络结构较差，Adam 获取的网络结构几乎全部预测正确；表2 中AdamU 方法的AUROC 和AUPR 分别为0.825、0.744，Adam 的AUROC 和AUPR 均等于1，达到了完美重构效果。

Table 2 Performance comparison of two training methods for Lorenz-96 model表2 Lorenz-96模型的两种训练方法性能比较

Fig.5 Results of two training methods for Lorenz-96 model图5 Lorenz-96模型的两种训练方法结果

通过线性VAR 模型和Lorenz-96 模型的仿真发现，有无正则项对模型最终的训练结果影响较大，因此在仿真后续部分将仅基于Adam 方法进行训练。

此外，为了考察不同非线性程度F和隐藏层单元数D对模型的影响，基于Adam 方法对不同F和D数值进行消融实验，比较结果如表3、表4 所示。由此可知，在不同D的情况下随着F增加，AUROC、AUPR 均会下降；在F=10时随着D增加AUROC 和AUPR 变化不大；当F={20，30，40}时，随着D增加AUROC、AUPR 均得到了不同程度的提升。

Table 3 AUROC for different F and D表3 不同F与D情况下的AUROC

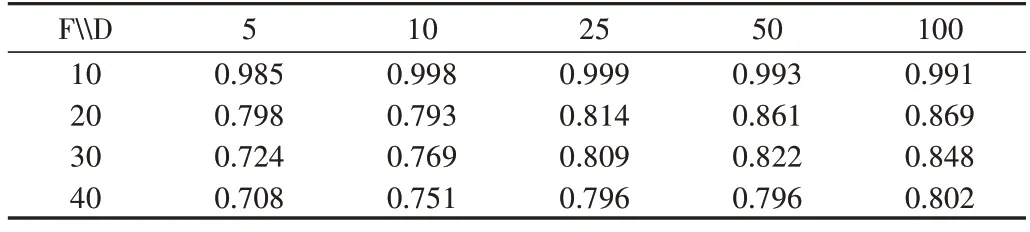
Table 4 AUPR for different F and D表4 不同F与D情况下的AUPR

总之，随着数据的非线性增强，GRU 网络的拟合能力变弱。在非线性程度较低时，增加隐藏层单元数无法大幅度提升模型精度；在非线性程度较高时，增加隐藏层单元数能明显提升模型精度，尤其在D从5 增加到10、从10 增加到25 时，AUROC 和AUPR 提升最明显，这也符合实际经验，在数据较复杂时模型精度往往会降低，可通过采用更复杂的模型提升表达能力。并且，在神经网络学习中增加网络深度和宽度是提高精度的常见方法［29］。

3.3 非线性VAR

一种非线性VAR 模型如式（15）所示，生成T=1 000的多变量时间序列矩阵，非线性VAR 模型基准网络如图6所示。

Fig.6 Benchmark network of nonlinear VAR model图6 非线性VAR模型的基准网络

网络训练采用Adam 优化方法，GRU 网络模型的隐藏层单元数=100，最大滞后阶数P=10，正则系数λ=0.14，学习率lr=0.001，训练步长为5 600。

训练完成后提取格兰杰因果矩阵如图7 所示，然后绘制ROC 曲线和PR 曲线如图8 所示。由图8 进一步计算ROC 曲线和PR 曲线的面积，即AUROC、AUPR 分别为0.915和0.876。

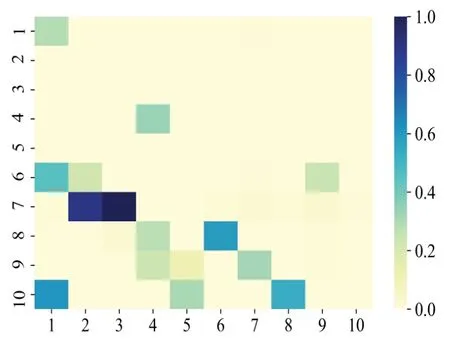
Fig.7 Granger causal matrix inferred by GRUGC图7 GRUGC的格兰杰因果矩阵

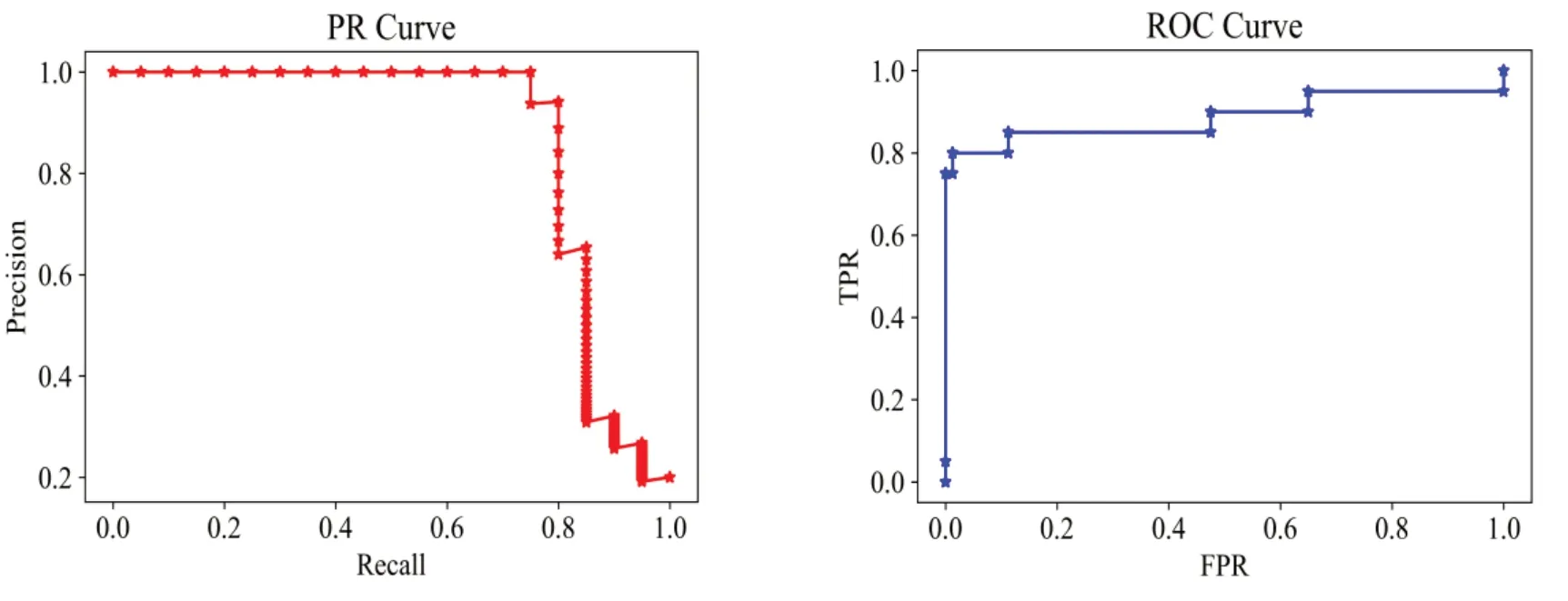
Fig.8 PR and ROC curve in the simulation of nonlinear VAR model图8 非线性VAR模型仿真的PR、ROC曲线

式中：xi，t为第i个节点在t时刻的值；i=1，2，…，10；εi，t～N(0，0.012)。

3.4 非均匀嵌入时滞VAR

根据式（16）研究一种非均匀嵌入时滞VAR 模型，其与非线性VAR 模型的不同之处在于节点间存在多阶滞后关系，生成T=1 000 的多变量时间序列矩阵，非均匀嵌入时滞VAR 模型基准网络如图9 所示。网络训练采用Adam优化方法，GRU 网络模型的隐藏层单元数D=100，最大滞后阶数P=5，正则系数λ=0.14，学习率lr=0.001，训练步长为5 600。训练完成后提取格兰杰因果矩阵如图10 所示，然后绘制ROC 曲线和PR 曲线如图11 所示，经过计算AUROC、AUPR 分别为0.904和0.921。仿真实验表明，GRUGC可处理非均匀嵌入时滞的复杂非线性数据，且在整体上性能较好。

Fig.9 Benchmark network of non-uniformly embedded time-delay VAR model图9 非均匀嵌入时滞VAR模型基准网络

Fig.10 Granger causality matrix for non-uniformly embedded timedelay VAR model图10 非均匀嵌入时滞VAR模型的格兰杰因果矩阵

Fig.11 PR，ROC curve in the simulation of non-uniformly embedded time-delay VAR model图11 非均匀嵌入时滞VAR模型仿真的PR、ROC曲线

式中：xi，t为第i个节点在t时刻的值；i=1，2，…，5；εi，t～N(0，0.012)。

3.5 DREAM3数据实验

为了验证GRUGC 在实际网络数据集上的性能，基于DREAM3 挑战赛中的两个Ecoli 数据集和3 个Yeast 数据集（https：//doi.org/10.7303/syn2853594）进行仿真研究。实验采取N=10 的小网络模型，在5 个数据集中每个数据集分别包含10 个不同的时间序列。针对每个时间序列重复试验4次，每次采集21个时间点，总共为84个样本点。

神经网络训练方法采用Adam 优化方法，GRU 网络模型的隐藏层单元数D=5，正则系数λ=0.18，学习率lr=0.001，训练步长为5 000。首先画出ROC 曲线和PR 曲线，如图12 所示；然后计算AUPR、AUROC，并分别与DREAM3挑战赛的最终获奖榜单的第一名bteam、第二名Team291和第三名Team304 进行比较；最后画出AUPR 和AUROC 的柱状图，如图13所示。

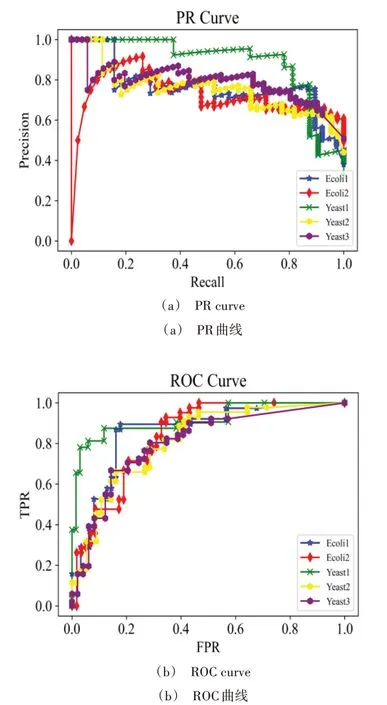
Fig.12 PR curve and ROC curve in the simulation of DREAM3图12 DREAM3仿真的PR曲线和ROC曲线

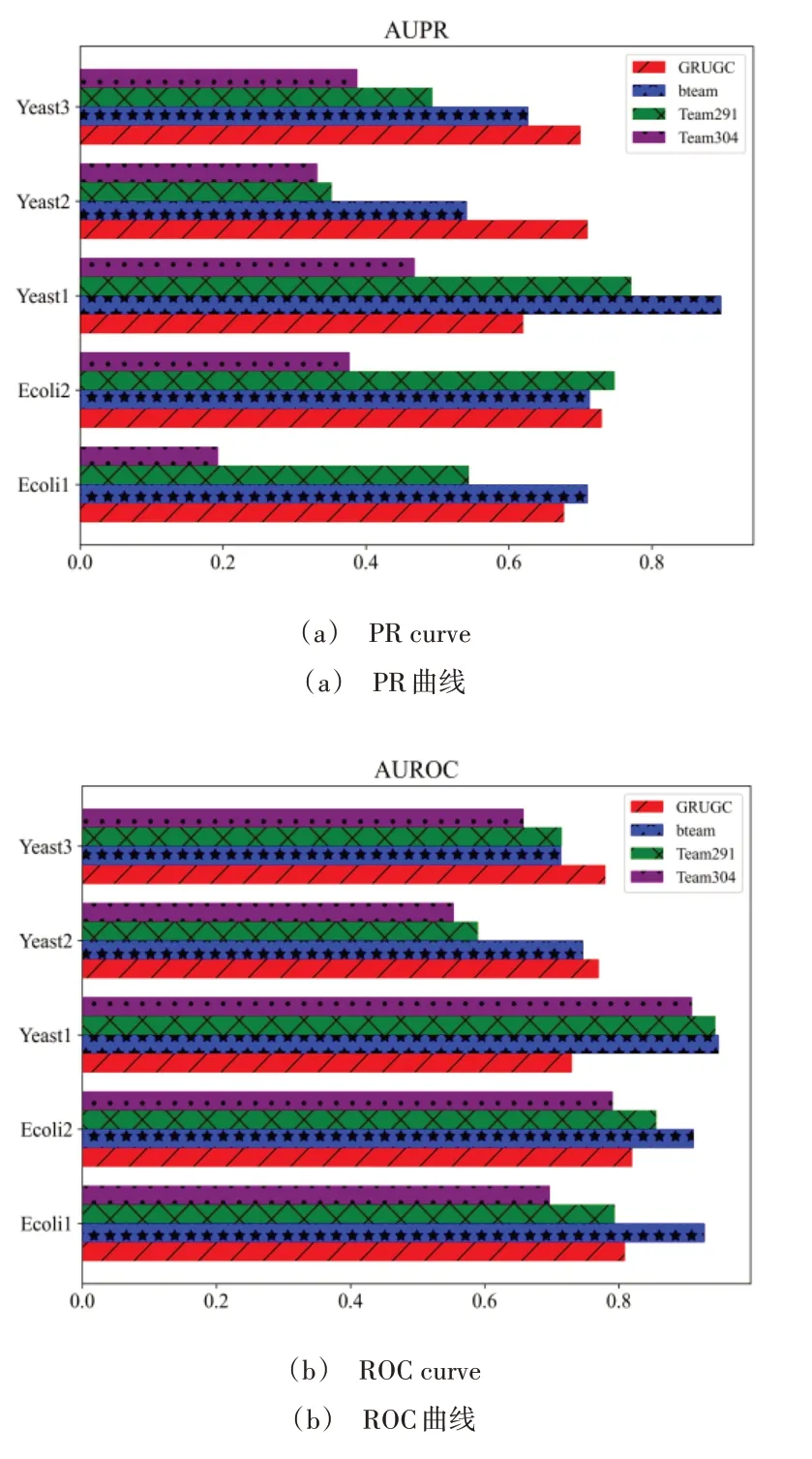
Fig.13 Performance comparison among GRUGC and top three methods in DREAM3图13 GRUGC与DREAM3前三名方法的性能比较

由图13 可见，GRUGC 在Yeast2、Yeast3 数据集 上的AUROC 和AUPR 均超过前3 名，而在Yeast1 数据集上GRUGC 的AUROC 不如前3 名，但AUPR 超过了Team304。同时，在Ecoli1、Ecoli2 数据集上GRUGC 的AUPR 与bteam获得的AUPR 值更接近，同时GRUGC 的AUROC 也能保持不错的效果。

表5 为对5 个数据集的AUROC、AUPR 取平均值进行综合分析。由此可知，GRUGC 的整体性能超过了第二名Team291，仅次于第一名bteam，尤其是AUPR 的平均值与bteam 值非常接近。通过DREAM3 挑战赛的研究分析发现，GRUGC 方法性能较好，具有一定的实际竞争力。

Table 5 Comparison analysis of mean AUROC and AUPR表5 AUROC和AUPR的均值对比分析

4 结语

网络重构旨在基于测量得到的数据推断网络节点间的相互作用关系，是分析系统动力学行为、结构特性和影响机制的前提和基础。本文将GRU 神经网络模型和格兰杰因果理论相结合，提出基于GRU 网络的格兰杰因果网络重构方法（GRUGC）。该方法考虑了变量间影响关系的非线性和因果性，从建模和分析中发现正则项对最终结果影响较大，有正则项的优化方法Adam 的性能相较于无正则项的AdamU 效果更好，而且当输入数据为长时间序列时GRUGC 不会发生梯度消失或梯度爆炸现象。

首先，通过对线性VAR、非线性VAR、Lorenz-96 和非均匀嵌入时滞VAR 模型的仿真研究证实了所提方法的有效性，然后在不同网络参数下对Lorenz-96 模型进行了消融实验，以进一步验证本文方法的性能。最后，基于DREAM3 挑战赛的Ecoli 和Yeast 数据集，与最终榜单的前3 名算法进行比较分析来验证GRUGC 方法的优越性和实用性。

在GRUGC 方法中使用的正则项对结果影响较大，因此需要更深入地研究正则项的影响机制，并提供更优的正则化方法。在应用GRUGC 进行网络重构时，还需考虑数据的质量以保证结果的准确性和可靠性。下一步，将深入拓展GRUGC 的适用范围，探索图像、文本等不同数据类型的应用。此外，对于存在多种因果关系的网络，探索如何选择最优的因果关系，并提供相应的可解释方法也是未来研究的热点之一。